Optimal transmission code reading at the back end

superglue.py

Acquisition of descriptor and location information

The above is very detailed. You can clearly see the process of the whole network here
In the superblue code, the author only provided the trained weight file and network process, but the training details were not given in the code. In the follow-up, I want to design my own loss and try to train myself. I see that this year's matching competitions are all things I have changed on superblue

SuperGlue feature matching middle-end
Given two sets of keypoints and locations, we determine the
correspondences by:
1. Keypoint Encoding (normalization + visual feature and location fusion)
2. Graph Neural Network with multiple self and cross-attention layers
3. Final projection layer
4. Optimal Transport Layer (a differentiable Hungarian matching algorithm)
5. Thresholding matrix based on mutual exclusivity and a match_threshold
The correspondence ids use -1 to indicate non-matching points. Paul-Edouard Sarlin, Daniel DeTone, Tomasz Malisiewicz, and Andrew
Rabinovich. SuperGlue: Learning Feature Matching with Graph Neural
Networks. In CVPR, 2020. https://arxiv.org/abs/1911.11763

(1) Network input

    """Run SuperGlue on a pair of keypoints and descriptors"""
    desc0, desc1 = data['descriptors0'], data['descriptors1']
    kpts0, kpts1 = data['keypoints0'], data['keypoints1']

This input is the output of SuperPoint. As the input of this network, it is the position information of descriptor and key frame respectively. Just take a look here.

(2) MLP module

In the previous one, the descriptors are regularized, which will not be repeated. The main function is to say that the weight of location information is the same as that of descriptors.
The most important thing is that the MLP module is actually the fusion module, which is equivalent to the fusion coding of position information and descriptor information, and the convolution operation is carried out in the middle.

(3) Attention module

This should be the main point, but I don't think there are many places that can be changed, so I didn't look carefully,

(4) Optimal transmission

I want to do research mainly in this position. I found a lot of data to see that the knowledge here is still profound. According to the author's logic, I probably understand that the author has generated a two-dimensional cost matrix in the above matrix, which is a little different from the optimal transmission theory. Here, a score I debug is a [1 * 239 * 244] dimensional two-dimensional matrix

scores = torch.einsum('bdn,bdm->bnm', mdesc0, mdesc1)
        scores = scores / self.config['descriptor_dim']\*\*.5

Before entering the optimal transmission module, the author directly obtains a coupling matrix through the above operation, which can correspond to the optimal transmission module.

        scores = log_optimal_transport(
            scores, self.bin_score,
            iters=self.config['sinkhorn_iterations'])

The parameter scores in this is the above, and then the bin_ At the beginning, I didn't understand what it was. After reading his paper, I found that he was actually a constant.

def log_optimal_transport(scores, alpha, iters: int):
    """ Perform Differentiable Optimal Transport in Log-space for stability"""
    b, m, n = scores.shape
    one = scores.new_tensor(1)
    k= m \* one
    ms, ns = (k).to(scores), (n\*one).to(scores)
    # Initializes a bmn matrix with a value of alpha
    bins0 = alpha.expand(b, m, 1)
    bins1 = alpha.expand(b, 1, n)
    alpha = alpha.expand(b, 1, 1)
    # Connect a new matrix
    couplings = torch.cat([torch.cat([scores, bins0], -1),
                           torch.cat([bins1, alpha], -1)], 1)

The alpha here corresponds to the bin above_ Score, the main function here. I think what the author wrote is a trash can defined by him. I don't understand its function. This thing expands a row and a column in the original two-dimensional matrix. The initial value in this matrix is alpha. A new matrix is obtained. The coupling matrix becomes [1 * 240 * 245]
Then there are the ns and ms. in fact, this thing is particularly cumbersome. This thing frankly corresponds to the probability function in the optimal transmission problem. Here we are really useless, because the probability assigned to each point must be the same (although I don't know how to correspond to the function of optimal transmission).

norm = - (ms + ns).log()
    log_mu = torch.cat([norm.expand(m), ns.log()[None] + norm])
    log_nu = torch.cat([norm.expand(n), ms.log()[None] + norm])
    log_mu, log_nu = log_mu[None].expand(b, -1), log_nu[None].expand(b, -1)

    Z = log_sinkhorn_iterations(couplings, log_mu, log_nu, iters)

I'm not particularly clear about the operation here. To put it bluntly, I understand that in order to raise the probability function required for superposition, here is log_mu and log_nu these two should be 1 * 240 and 245 * 1 respectively
Then you can get this Z

sinkhorn iterative process

	def log_sinkhorn_iterations(Z, log_mu, log_nu, iters: int):
    """ Perform Sinkhorn Normalization in Log-space for stability"""
    u, v = torch.zeros_like(log_mu), torch.zeros_like(log_nu)
    for _ in range(iters):
        u = log_mu - torch.logsumexp(Z + v.unsqueeze(1), dim=2)
        v = log_nu - torch.logsumexp(Z + u.unsqueeze(2), dim=1)
    return Z + u.unsqueeze(2) + v.unsqueeze(1)

The author said that he used a differential Hungarian matching algorithm to solve it. From my understanding, it seems that this thing is to amplify the difference of matching
It's superimposed 100 times. It seems that u and v, I can understand that the joint probability distribution is equivalent to matrix Z, and log_mu and log_nu is equivalent to the boundary probability distribution. The difference is increased by continuously superimposing the boundary probability distribution.
(whisper it here. I feel this thing is useless, because after I remove this thing, there is no difference in the matching with my naked eye.) it may also be that I am too superficial to see the role of the author adding this thing, and I have seen a lot of relevant work because I want to modify it to improve this performance. The main function of this Sinkhorn is that the superposition efficiency is relatively high. This effect must be much better than the violent matching used by orb-slam2. Moreover, the addition of attention, especially self attention, in front of it can certainly improve the information of the descriptor here. But I feel this sinkhorn_iterations in areas with special texture repetition, its role is not as big as the previous one, and Sinkhorn can not solve an accurate solution, but only an approximate solution.

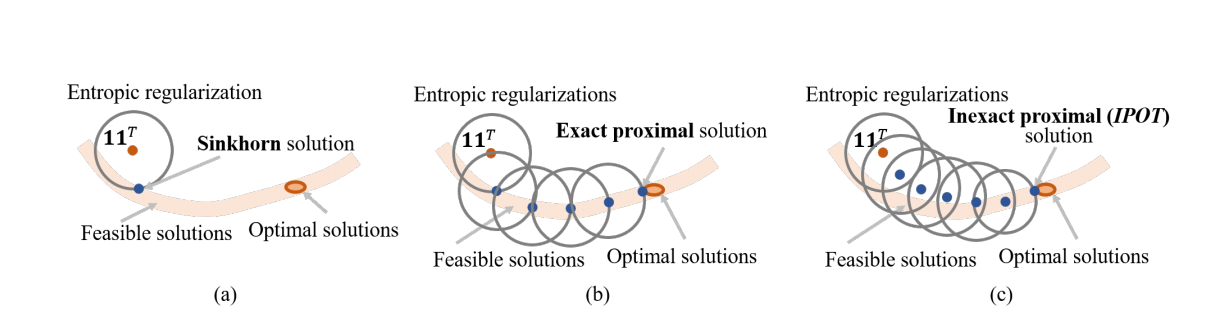
This picture is very intuitive. This iterative process is actually very extensive. I want to improve it. Moreover, there is little difference between the two adjacent frames of the scene in slam, especially for the location information, so I feel that generally speaking, the order of taking points is not much different from the matching order, except for some missing matching points.

Result analysis

        mutual0 = arange_like(indices0, 1)[None] == indices1.gather(1, indices0)
        mutual1 = arange_like(indices1, 1)[None] == indices0.gather(1, indices1)
        zero = scores.new_tensor(0)
        #torch.where()
        #The function combines two tensor types according to certain rules.
        #torch.where(condition, a, b) where
        #Input parameter condition: condition limit. If the condition is met, select a; otherwise, select b as the output.
        mscores0 = torch.where(mutual0, max0.values.exp(), zero)
        mscores1 = torch.where(mutual1, mscores0.gather(1, indices1), zero)
        valid0 = mutual0 & (mscores0 > self.config['match_threshold'])
        valid1 = mutual1 & valid0.gather(1, indices1)
        indices0 = torch.where(valid0, indices0, indices0.new_tensor(-1))
        indices1 = torch.where(valid1, indices1, indices1.new_tensor(-1))
        return {
            'matches0': indices0, # use -1 for invalid match
            'matches1': indices1, # use -1 for invalid match
            'matching_scores0': mscores0,
            'matching_scores1': mscores1,
        }

There is no need to put too much here. The author finally threw away the trash can. I suddenly found that the function of this trash can is to make the unmatched points have a place to go, so that he can't occupy the magpie's nest. If these wrong points can't work, get him a matching trash can. Finally, when he wants to go to the trash can, he turns these points to the trash can into invalid points.