In JDK 1.8, the bottom layer of HashMap is stored in array Node < K, V > array. Each element in the array is stored in a linked list. When the element exceeds 8, the linked list is converted into a mangrove storage.
red-black tree
The red-black tree is essentially a balanced search Binary tree, which is used to store ordered data. Compared with the linked list data search, the time complexity of the linked list is O(n), and the time complexity of the red-black tree is O(lgn).
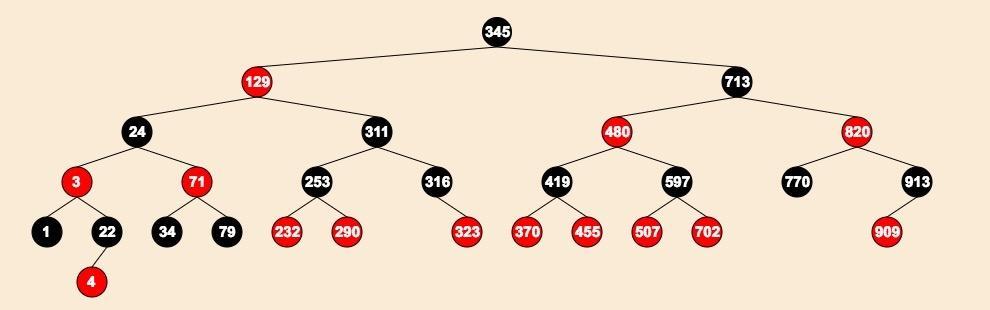
The mangrove tree needs to satisfy five characteristics:
- Each node is red or black
- The root node is black
- Every empty leaf node must be black
- The child nodes of the red node must be black
- Black Nodes Arriving at Any Subnode Containing the Same Array
When new nodes or fewer nodes are added, the tree structure will be adjusted by left-handed or right-handed operations to meet the above characteristics.
TreeNode class
The red and black trees in HashMap are constructed through the TreeNode class. TreeNode is a static inner class of HashMap, inheriting from LinkedHashMap. Entry < K, V > class
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> { // Parent node TreeNode<K,V> parent; // red-black tree links // Left child node TreeNode<K,V> left; // Right child node TreeNode<K,V> right; // Front node TreeNode<K,V> prev; // needed to unlink next upon deletion boolean red; TreeNode(int hash, K key, V val, Node<K,V> next) { super(hash, key, val, next); } ... }
treeifyBin method
When the put method in HashMap is used, but when the length of the list in an array is longer than 8, the treeifyBin method is called to convert the list into a red-black tree.
final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e; if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) // If the array size is less than 64, call resize to expand the array size to 2 times resize(); else if ((e = tab[index = (n - 1) & hash]) != null) { TreeNode<K,V> hd = null, tl = null; // Traversing the list, transforming the list elements into TreeNode chains do { // Call replacementTreeNode to construct TreeNode TreeNode<K,V> p = replacementTreeNode(e, null); if (tl == null) // The TreeNode chain is empty and the element is set to the first node of hd hd = p; else { // TreeNode chain is not empty, add elements to the back of TreeNode chain p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null); if ((tab[index] = hd) != null) // TreeNode Link List Converted to Red-Black Tree hd.treeify(tab); } }
Constructing Red-Black Trees--treeify Method
The treeify method is a method of the TreeNode class, which converts the Treenode chain into a red-black tree.
final void treeify(Node<K,V>[] tab) { TreeNode<K,V> root = null; for (TreeNode<K,V> x = this, next; x != null; x = next) { // Traversing TreeNode Chain next = (TreeNode<K,V>)x.next; x.left = x.right = null; if (root == null) { // Setting up root node x.parent = null; x.red = false; root = x; } else { K k = x.key; int h = x.hash; Class<?> kc = null; for (TreeNode<K,V> p = root;;) { // Loop to find where the current node is inserted and add nodes int dir, ph; K pk = p.key; // The hash value of the hashMap element is used to represent the node value size in the red-black tree. if ((ph = p.hash) > h) // The current node value is less than the root node, dir = 1 dir = -1; else if (ph < h) // The current node value is greater than the root node, dir = 1 dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) // The value of the current node is equal to the value of the root node. // If the current node implements the Comparable interface, call compareTo to compare the size and assign dir // If the current node does not implement the Comparable interface and the compareTo result is equal to 0, the tieBreakOrder is called to continue comparing sizes. // The essence of tieBreakOrder is to compare hashcode between k and pk. dir = tieBreakOrder(k, pk); // The current "root node" is assigned to xp TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { // If the current node is smaller than the root node and the left child node is empty or the current node is larger than the root node and the right child node is empty, add the child node directly. x.parent = xp; if (dir <= 0) xp.left = x; else xp.right = x; // Balanced red and black trees root = balanceInsertion(root, x); // Jump out of the loop and continue to add the next element to the red-black tree break; } } } } // Ensure that the red-black tree root node is the first node of the index in the array moveRootToFront(tab, root); }
Balanced Red-Black Tree after Adding Elements--Balanced Insertion Method
When adding new nodes in the red-black tree, we need to call balance Insertion method to ensure the characteristics of the red-black tree.
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { // New nodes default to red x.red = true; // xp parent node xpp grandfather node xppl grandfather left node xppr grandfather right node for (TreeNode<K,V> xp, xpp, xppl, xppr;;) { if ((xp = x.parent) == null) { // The parent node of X is empty, x should be the root node, and X should be black. x.red = false; return x; } else if (!xp.red || (xpp = xp.parent) == null) // The parent node is black, the grandfather node is empty, and returns directly return root; // The parent node is red if (xp == (xppl = xpp.left)) { // The parent node is the left node of the grandfather node if ((xppr = xpp.right) != null && xppr.red) { // Uncle node is red // Uncle node set to black xppr.red = false; // The parent node is set to black xp.red = false; // Grandfather node set to red xpp.red = true; // Set the grandfather node to the current node and continue to loop x = xpp; } else { // Uncle node is black or empty if (x == xp.right) { // If x is the right node of the parent node, the left-hand operation is required. root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } // Left node through left-hand x if (xp != null) { // Parent node painted black xp.red = false; if (xpp != null) { // Grandfather node is not empty // Grandfather node set to red xpp.red = true; // Rotate right with rented parent node as fulcrum root = rotateRight(root, xpp); } } } } else { // The father node is the right node if (xppl != null && xppl.red) { // Uncle node is red // Set uncle node to black xppl.red = false; // The parent node is set to black xp.red = false; // Grandfather node set to red xpp.red = true; // Cyclic operation x = xpp; } else { if (x == xp.left) { // Dextral rotation root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } // x is the right node if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; // Left-handed with grandfather node as fulcrum root = rotateLeft(root, xpp); } } } } } }
Adding Elements to the Red-Black Tree--putTreeVal Method
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab, int h, K k, V v) { Class<?> kc = null; boolean searched = false; // Get the root node TreeNode<K,V> root = (parent != null) ? root() : this; for (TreeNode<K,V> p = root;;) { // Traverse from the root node int dir, ph; K pk; // Determine where to add elements by comparing hash sizes if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((pk = p.key) == k || (k != null && k.equals(pk))) // The same key returns directly return p; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { if (!searched) { TreeNode<K,V> q, ch; searched = true; // Direct return with the same node if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } TreeNode<K,V> xp = p; // Adding elements according to dir size if ((p = (dir <= 0) ? p.left : p.right) == null) { Node<K,V> xpn = xp.next; // Building a new treeNode node TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); if (dir <= 0) xp.left = x; else xp.right = x; xp.next = x; x.parent = x.prev = xp; if (xpn != null) ((TreeNode<K,V>)xpn).prev = x; // Balancing the red-black tree and ensuring that root is the first node of index moveRootToFront(tab, balanceInsertion(root, x)); return null; } } }
TreeNode class also has many methods, such as deleting the red-black tree node method removeTreeNode, deleting the balanced binary tree method balance Deletion, looking for the red-black tree node method getTreeNode.... There is energy for further analysis.