1 Definition

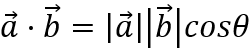
You know, dot product gives a scalar, what does this scalar mean?

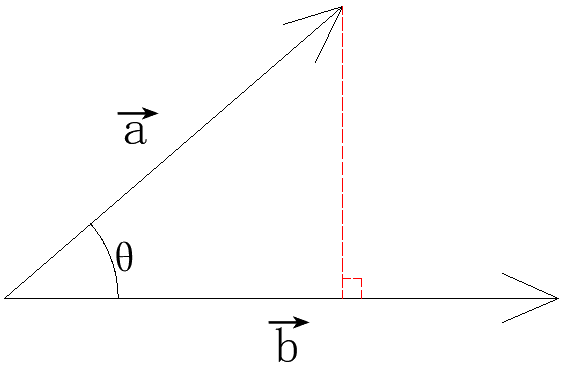
2 Geometric Meaning

If b ⃗ \vec{b} b Is a unit vector, then a vector a ⃗ \vec{a} a In vector b ⃗ \vec{b} b The projection length on the.

3 vector a. vector b = xaxb+yayb+zazb

How did the above formula come about?
set up

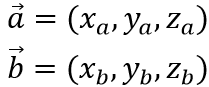
According to the Cosine Theorem,

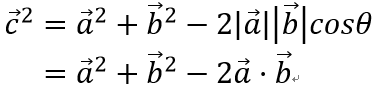
therefore

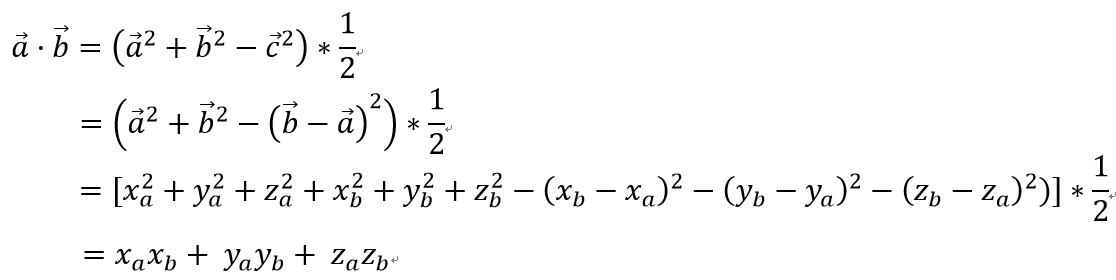
4 Application Cases

4.1 Find the angle between two vectors

Known Vector

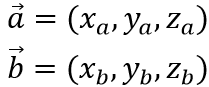
According to the definition of point product, there are

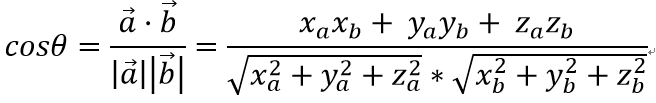
Of course, this method Unity has already packaged for me. Let's ask for the angle between two vectors, just use Vector 3.Angle. The source code for Vector 3.Angle is as follows, and you can see that the above formula is actually implemented inside.

    /// <summary>
    ///   <para>Returns the angle in degrees between from and to.</para>
    /// </summary>
    /// <param name="from">The vector from which the angular difference is measured.</param>
    /// <param name="to">The vector to which the angular difference is measured.</param>
    /// <returns>
    ///   <para>The angle in degrees between the two vectors.</para>
    /// </returns>
    public static float Angle(Vector3 from, Vector3 to)
    {
      float num = (float) Math.Sqrt((double) from.sqrMagnitude * (double) to.sqrMagnitude);
      if ((double) num < 1.00000000362749E-15)
        return 0.0f;
      return (float) Math.Acos((double) Mathf.Clamp(Vector3.Dot(from, to) / num, -1f, 1f)) * 57.29578f;
    }

4.2 Judging whether two vectors are vertical

When two vectors are perpendicular, the angle between them is 90 degrees, and COS is 90 degrees= 0, so a ⃗ \vec{a} a · b ⃗ \vec{b} b =0.
In other words, as long as a ⃗ \vec{a} a and b ⃗ \vec{b} b None of them are null vectors, as long as a ⃗ \vec{a} a · b ⃗ \vec{b} b =0 means that the two vectors are perpendicular.

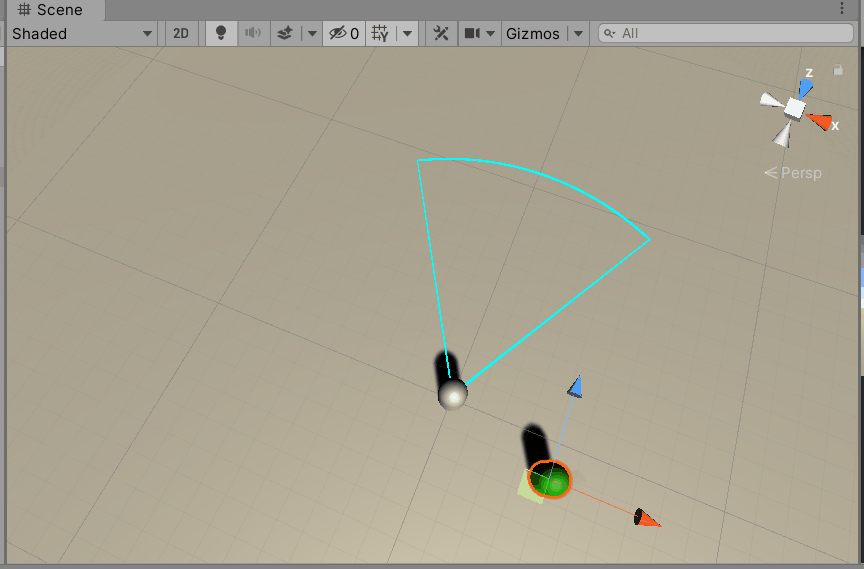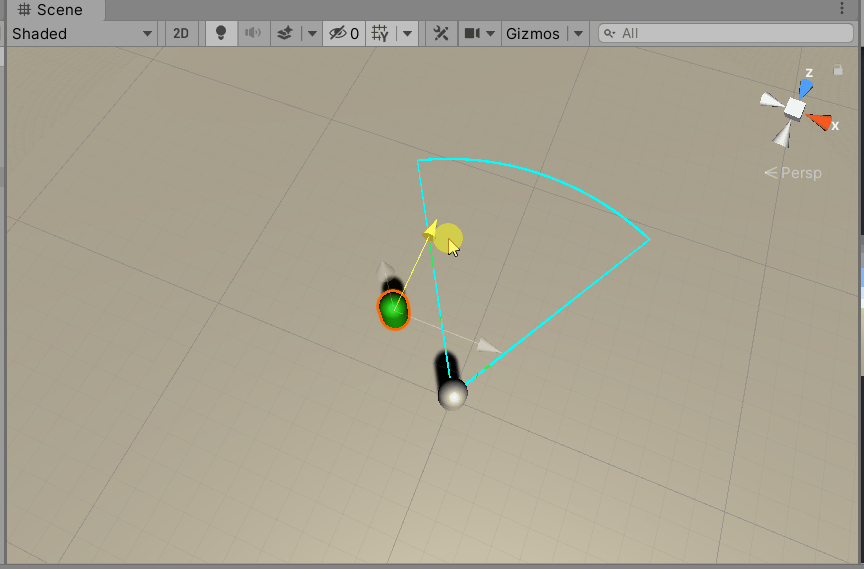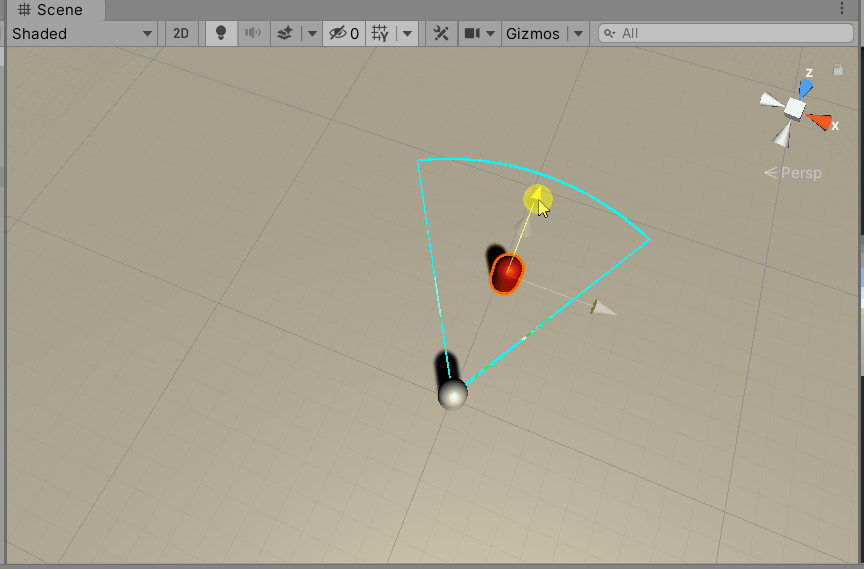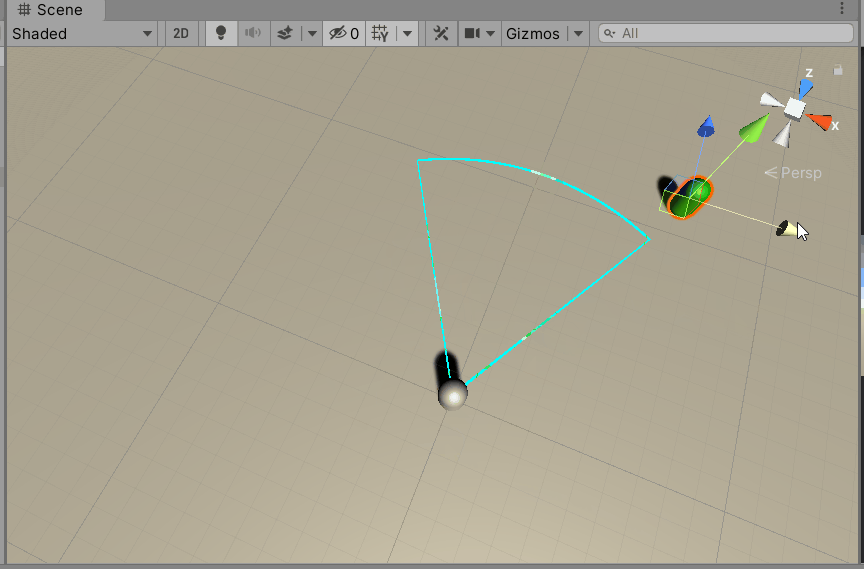
4.3 Determine whether NPC is within attack range

Assume that the player's attack range is 60 degrees from left to right and the maximum attack radius is 10. Set the player's position to A (xa, ya, za) and the monster's position to B(xb, yb, zb), to determine if the monster is within the range of a human attack?
It is very simple to determine if the distance between the two is less than 10, and if it is greater, it is not within the attack range.
Re-judgment A B ⃗ \vec{AB} AB Whether the angle in front of the player is less than 30 degrees, greater than it is not within the attack range, and less than or equal to it is within the attack range.
The code is also simple, and the distance between the two can be determined by Vector3.Distance. A B ⃗ \vec{AB} AB The angle in front of the player is calculated by Vector 3.Angle with the code below.

// Determine if targetPos is in line of sight
public bool IsInView(Vector3 targetPos)
{
    // Player Position
    Vector3 selfPos = m_GameObject.transform.position;

    if (Vector3.Distance(selfPos, targetPos) > 10f)
        return false;

    Vector3 loorDir = targetPos - selfPos;
    if (Vector3.Angle(loorDir, m_GameObject.transform.forward) < 30f)
        return true;

    return false;
}

Then test it in Unity. As you can see, our analysis is correct.

4.4 Known incident light and surface normal to find reflected light

As shown in the figure, the incoming light is known A O ⃗ \vec{AO} AO And surface normal n ⃗ \vec{n} n (assumed to be a unit vector), find the reflected light O B ⃗ \vec{OB} OB .

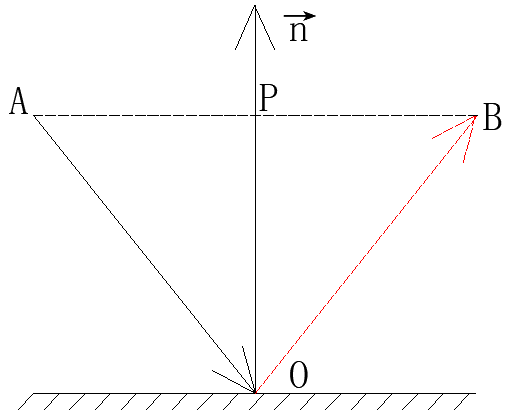
Look directly at the calculation process.

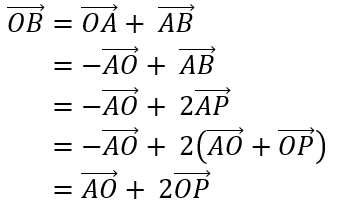
also

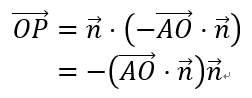
How did this formula come from above? Remember the geometric meaning of the dot product?

If b ⃗ \vec{b} b Is a unit vector, then a vector a ⃗ \vec{a} a In vector b ⃗ \vec{b} b The projection length on the.

There O P ⃗ \vec{OP} OP The length is not exactly O A ⃗ \vec{OA} OA In Unit Vector n ⃗ \vec{n} n Is the projection length on the. O P ⃗ \vec{OP} OP Multiply the length by its direction n ⃗ \vec{n} n Let's get it O P ⃗ \vec{OP} OP Yes.
The complete derivation is as follows.

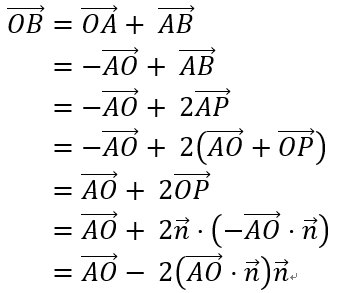
The code is as follows:

/// <summary>
///Calculate reflected light
/// </summary>
/// <param name="lightDir">incoming light</param>
/// <param name="normalDir">surface normal (unit vector)</param>
/// <returns>reflected light</returns>
private Vector3 CalcReflectDir(Vector3 lightDir, Vector3 normalDir)
{
    return lightDir - 2 * Vector3.Dot(lightDir, normalDir) * normalDir;
}

Verify in Unity.

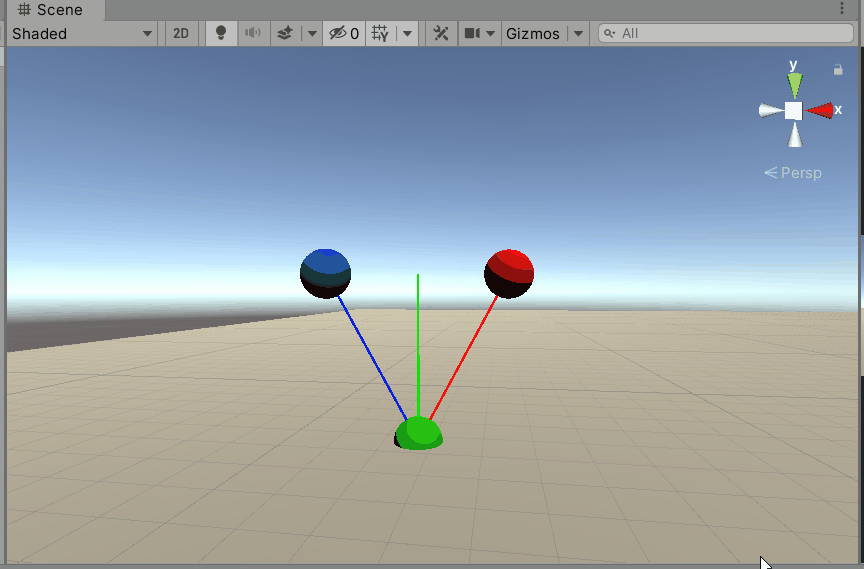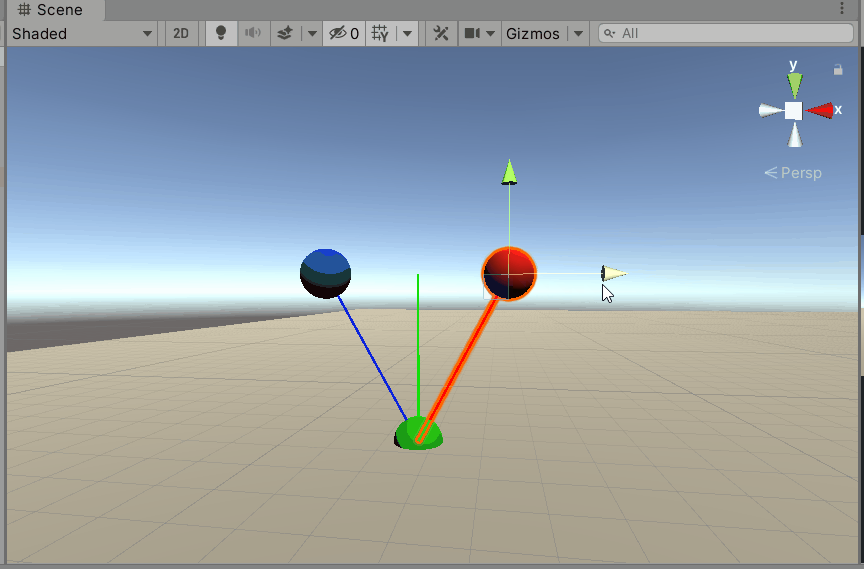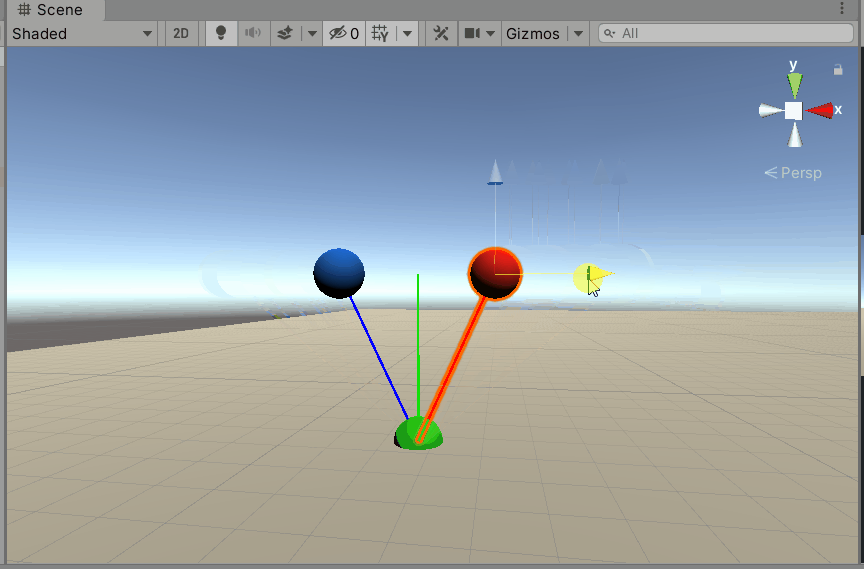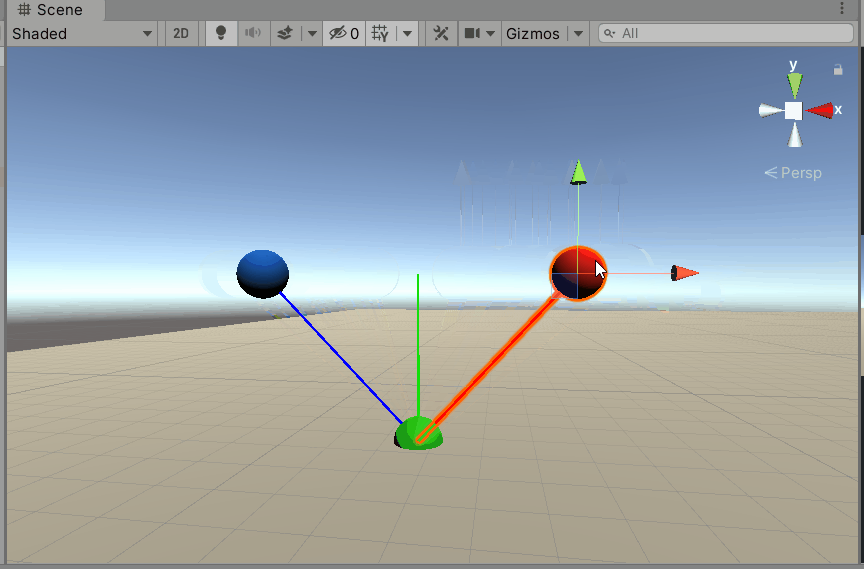
5 Projects

Links: https://pan.baidu.com/s/1Sv7CCrnh88MEvB6evW-rQg
Extraction Code: t4ix
Blogger Text Blog Link.