explain:

The methods used in this paper come from network search. This paper draws lessons from the articles of other bloggers and implements the Alpha Shapes algorithm on his basis. Then I wrote an Alpha Shapes demonstration program.
Alpha Shapes demo download

Data:
1. Click in the blank space to add data.
2. You can also directly click the random data button to randomly generate 50 data points.
3. Press Ctrl+Z to undo and delete the last added point.
Parameter setting:
The default setting radius of the demo program is 30. You can drag the slider to set the radius value, and the slider range is (0-200).
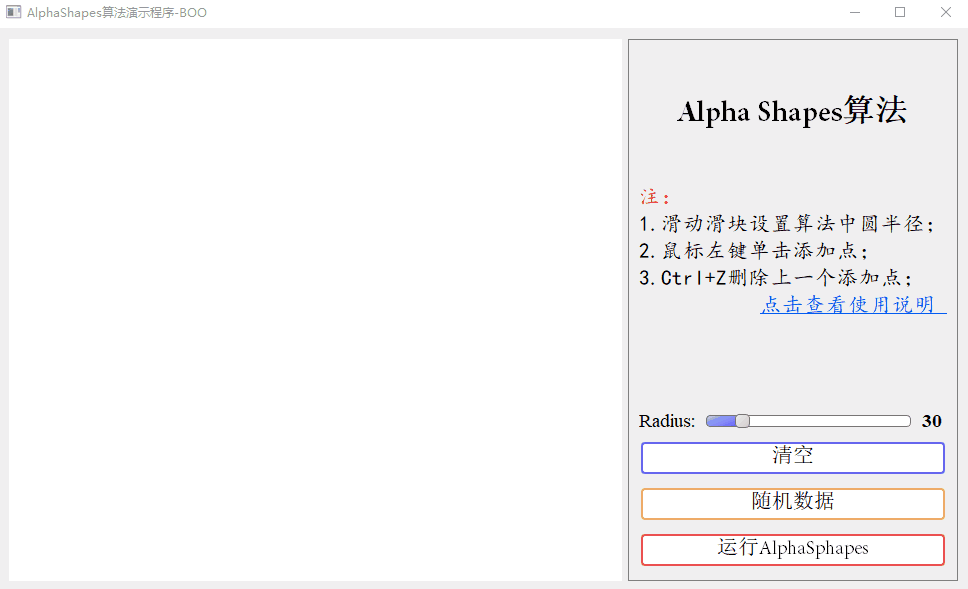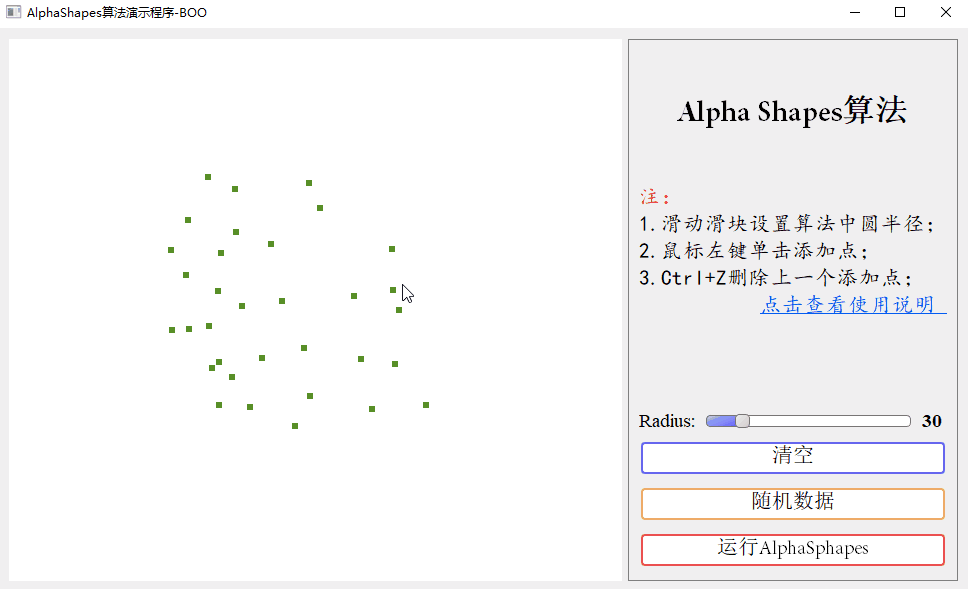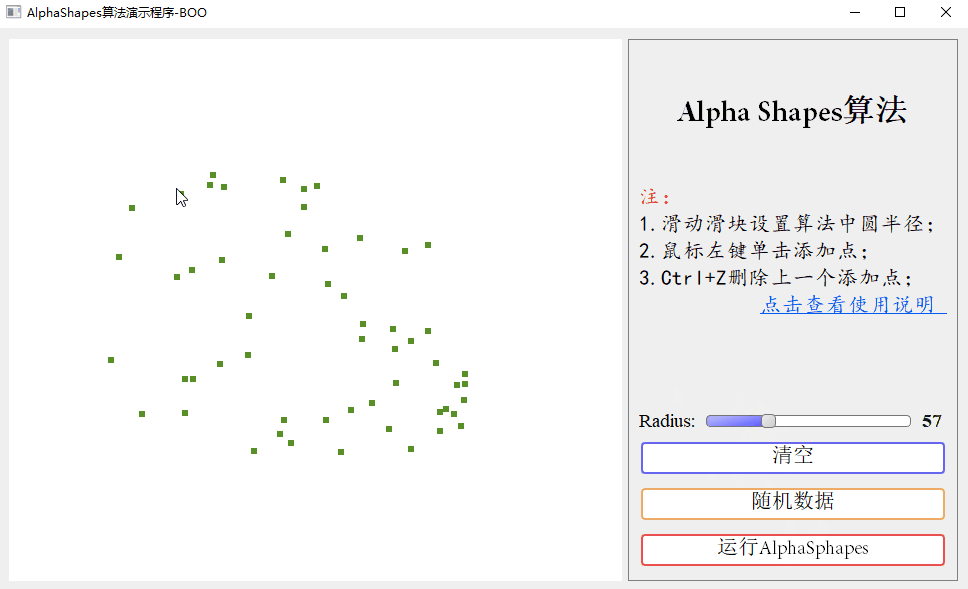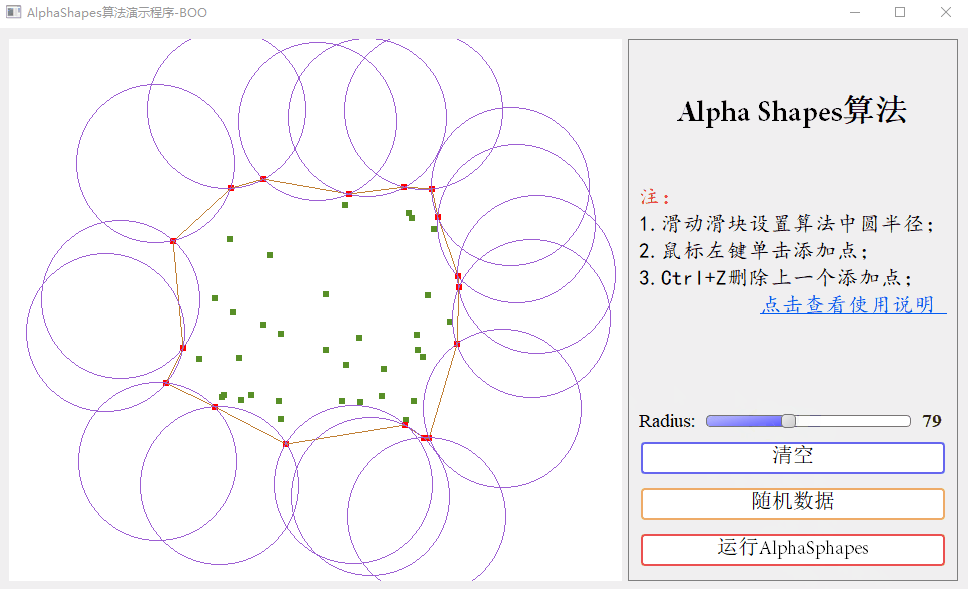
Click the run alphashapes button to draw.

Screenshot of software usage

PCL operation results

Principle of Alpha Shapes algorithm

Implementation process:
In the finite discrete point set S, there are N points, which can form N*(N-1) straight lines. We can extract the boundary points by judging whether the line segment is a boundary line. Boundary line judgment method: set a radius R, draw a circle with the endpoints (P1,P2) of each line segment (obviously, there are two such circles), and judge that there are no other points in the circle, then judge that the line segment is the boundary line, and P1,P2 are the boundary points.
Specific steps:
1. Traverse each edge
2. If it is determined that the length of P1P2 is greater than 2R, skip.
3. Find the center coordinates (C1,C2).
4. Judge that the interior of any circle does not contain other points in S, and P1 and P2 are boundary points.
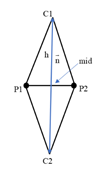
Solve the center of the circle (be sure to solve it with vectors. Other methods are prone to bugs).
1. Calculate the vector v1=P1-P2, the midpoint coordinate mid of the line segment,
2. According to the fact that the two vectors are perpendicular to 0, we can find n,
3. According to the triangle vertical theorem, the length h from C1 to segment P1P2 can be calculated,
4. In this way, the C1 and C2 coordinates C1 = mid + NH and C1 = mid NH can be calculated.

Code implemented in qt
This function is mainly implemented in qt. Most of it is directly copied from the first reference article. I added the record center and boundary points (in order). If you understand it, you can implement it in pcl. In fact, you only need to change the point type and write a distance calculation between two points.

//This function is directly copied from the first reference article. If you understand it, you can implement it in pcl
void alphaShapes::process()
{
	for (int i = 0; i<m_points.size(); i++)
	{
		// k starts from i+1 and reduces double counting
		for (int k = i + 1; k<m_points.size(); k++)
		{
			// Skip situations where the distance is greater than the diameter
			if (m_points[i].distanceToPoint(m_points[k])>2 * m_radius)
				continue;

			// Two centers
			QVector2D c1, c2;

			// Midpoint of line segment
			QVector2D center = 0.5*(m_points[i] + m_points[k]);

			// Direction vector d = (x,y)
			QVector2D dir = m_points[i] - m_points[k];

			// Vertical vector n = (a, b) a * dir. X + b * dir. Y = 0; a = -(b*dir.y/dir.x)
			QVector2D normal;
			normal.setY(5);  // Because there are two unknowns, just attach a value of 5 to y. 

			if (dir.x() != 0)
				normal.setX(-(normal.y()*dir.y()) / dir.x());
			else     // If the direction is parallel to the y axis
			{
				normal.setX(1);
				normal.setY(0);
			}
			normal.normalize();   // Normal vector unitization

			float len = sqrt(m_radius*m_radius - (0.25*dir.length()*dir.length()));
			c1 = center + len*normal;
			c2 = center - len*normal;

			// b1 and b2 record whether other points are found in circles C1 and C2.
			bool b1 = false, b2 = false;
			for (int m = 0; m<m_points.size(); m++)
			{
				if (m == i || m == k)
					continue;

				if (b1 != true && m_points[m].distanceToPoint(c1) < m_radius)
					b1 = true;
				if (b2 != true && m_points[m].distanceToPoint(c2) < m_radius)
					b2 = true;

				// If there are internal points, there is no need to continue the inspection
				if (b1 == true && b2 == true)
					break;
			}

			MyLine edge;
			if (b1 != true || b2 != true)
			{

				edge.p1.setX(m_points[i].x());
				edge.p1.setY(m_points[i].y());
				edge.p2.setX(m_points[k].x());
				edge.p2.setY(m_points[k].y());
			
				m_lines.push_back(edge);
			}
			if (!b1)
			{
				MyCircle c;
				c.c1.setX(c1.x());
				c.c1.setY(c1.y());
				c.radius = m_radius;
				m_circles.push_back(c);
			}
			if (!b2)
			{
				MyCircle c;
				c.c1.setX(c2.x());
				c.c1.setY(c2.y());
				c.radius = m_radius;
				m_circles.push_back(c);
			}
		}
	}
	takePoint();//Get boundary points
}

reference resources:
https://ryuzhihao123.blog.csdn.net/article/details/78130511?spm=1001.2101.3001.6650.6&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-6.highlightwordscore&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-6.highlightwordscore