1. Description of successive approximation algorithm

2.Verilog implementation

3. Written by testbench

1. Description of successive approximation algorithm

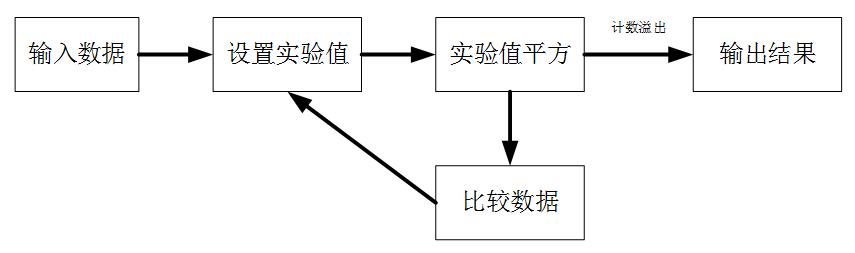
The flow of successive approximation algorithm is shown in Figure 1. First, input data[7:0], then set the experimental value d [3:0] and the determined value d [3:0], and then set each position 1 (e.g. d [3] to 1) in order from high to low, and then compare the experimental value with the input data. If the square of the experimental value is greater than the input value (d [Z ^ 2 > data), then this bit is 0 (d [Q [3] is 0). , otherwise ((D ﹐ Z ^ 2 ≤ data)), this bit is 1 (D ﹐ Q [3] is 1); this bit is iterated to the last bit.

It can be seen that n/2 iterations are required for n-bit data, and n/2 cycles are required for each calculation period.

The Figure1 block diagram of successive approximation algorithm

2.Verilog implementation

//////////////////////////////////////////////////////////////////////////////////



//



//			successive approximation algorithm 



//



module sqrt_1



	#( 	



			parameter  		 							d_width = 8,



			parameter       							q_width = d_width/2 - 1,



			parameter       							r_width = q_width + 1	)



	(



	input			wire									clk,



	input			wire									rst,



	input			wire									i_vaild,



	input			wire			[d_width:0]			data_i, //input



	



	



	output		reg									o_vaild,



	output		reg			[q_width:0]			data_o, //output



	output		reg			[r_width:0]			data_r  //Remainder



	



    );



//--------------------------------------------------------------------------------



	reg 							[d_width:0] 		D				[r_width:1]; //Number of squares



	reg 							[q_width:0] 		Q_z			[r_width:1]; //temporary



	reg	 						[q_width:0] 		Q_q			[r_width:1]; //confirm



	reg 													ivalid_t		[r_width:1];



//--------------------------------------------------------------------------------



	always@(posedge	clk or posedge	rst)



		begin



			if(rst)



				begin



					D[r_width] <= 0;




					Q_z[r_width] <= 0;



					Q_q[r_width] <= 0;



					ivalid_t[r_width] <= 0;



				end



			else	if(i_vaild)



				begin



					D[r_width] <= data_i;  //Data of the party under Exploitation



					Q_z[r_width] <= {1'b1,{q_width{1'b0}}}; //Experiment value setting



					Q_q[r_width] <= 0; //Actual calculation results



					ivalid_t[r_width] <= 1;



				end



			else



				begin



					D[r_width] <= 0;



					Q_z[r_width] <= 0;



					Q_q[r_width] <= 0;



					ivalid_t[r_width] <= 0;



				end



		end



//-------------------------------------------------------------------------------



//		Iterative calculation process



//-------------------------------------------------------------------------------



		generate



			genvar i;




				for(i=r_width-1;i>=1;i=i-1)



					begin:U



						always@(posedge clk or posedge	rst)



							begin



								if(rst)



									begin



										D[i] <= 0;




										Q_z[i] <= 0;




										Q_q[i] <= 0;




										ivalid_t[i] <= 0;




									end




								else	if(ivalid_t[i+1])



									begin




										if(Q_z[i+1]*Q_z[i+1] > D[i+1])



											begin



												Q_z[i] <= {Q_q[i+1][q_width:i],1'b1,{{i-1}{1'b0}}};




												Q_q[i] <= Q_q[i+1];



											end



										else



											begin



												Q_z[i] <= {Q_z[i+1][q_width:i],1'b1,{{i-1}{1'b0}}};



												Q_q[i] <= Q_z[i+1];



											end



										D[i] <= D[i+1];



										ivalid_t[i] <= 1;



									end



								else



									begin



										ivalid_t[i] <= 0;



										D[i] <= 0;



										Q_q[i] <= 0;



										Q_z[i] <= 0;



									end



							end



					end



		endgenerate



//--------------------------------------------------------------------------------



//	Calculate remainder and final square root



//--------------------------------------------------------------------------------



		always@(posedge	clk or posedge	rst) 



			begin



				if(rst)



					begin



						data_o <= 0;



						data_r <= 0;



						o_vaild <= 0;



					end



				else	if(ivalid_t[1])



					begin




						if(Q_z[1]*Q_z[1] > D[1])



							begin



								data_o <= Q_q[1];




								data_r <= D[1] - Q_q[1]*Q_q[1];



								o_vaild <= 1;




							end




						else




							begin




								data_o <= {Q_q[1][q_width:1],Q_z[1][0]};




								data_r <= D[1] - {Q_q[1][q_width:1],Q_z[1][0]}*{Q_q[1][q_width:1],Q_z[1][0]};



								o_vaild <= 1;




							end




					end




				else




					begin




						data_o <= 0;




						data_r <= 0;




						o_vaild <= 0;




					end




			end




//--------------------------------------------------------------------------------

 3.Testbench To write

//--------------------------------------------------------------------------------
	`define  		 						d_w 		 8
	`define        						q_w		 `d_w / 2
	`define        						r_w 		 `q_w + 1
//--------------------------------------------------------------------------------
module tb_sqrt;
//--------------------------------------------------------------------------------
	// Inputs
	reg 										clk;
	reg 										rst;
	reg					 					i_vaild;
	reg 			[`d_w-1:0] 				data_i;

	// Outputs
	wire 										o_vaild;
	wire 			[`q_w-1:0]				data_o;
	wire 			[`r_w-1:0]				data_r;

//--------------------------------------------------------------------------------
	// Instantiate the Unit Under Test (UUT)
	sqrt_1 
	#(
		.d_width		( 	`d_w-1		),
		.q_width 	(	`q_w-1		),
		.r_width 	(  `r_w-1		)	
	)
		uut 
	(
		.clk			(	clk			), 
		.rst			(	rst			), 
		.i_vaild		(	i_vaild		), 
		.data_i		(	data_i		), 
		.o_vaild		(	o_vaild		), 
		.data_o		(	data_o		), 
		.data_r		(	data_r		)
	);
//--------------------------------------------------------------------------------
	initial begin
		// Initialize Inputs
		clk = 0;
		rst = 1;
		// Wait 100 ns for global reset to finish
		#100;
      rst = 0; 
		// Add stimulus here

	end
    
	always #5 clk  = ~ clk ;
	
	reg	[`d_w:0]		cnt ;
	
	reg	[31:0]		a ;
//--------------------------------------------------------------------------------
	always@(posedge	clk or posedge	rst)
		begin
			if(rst)
				begin
					i_vaild <= 0;
					data_i <= 0;
					cnt <= 0;
				end
			else	if(cnt < 10)
				begin
					i_vaild <= 1;
					data_i <= {$random} % 255;
					cnt <= cnt + 1;
				end
			else
				begin
					i_vaild <= 0;
					data_i <= 0;
					cnt <= cnt;
				end
		end
//--------------------------------------------------------------------------------
endmodule