The RAPIDS cuGraph library is a set of graph analysis used to process data in GPU data frames - see cuDF. cuGraph is designed to provide NetworkX like API s that are familiar to data scientists, so they can now build GPU accelerated workflows more easily

Official documents:
rapidsai/cugraph
cuGraph API Reference

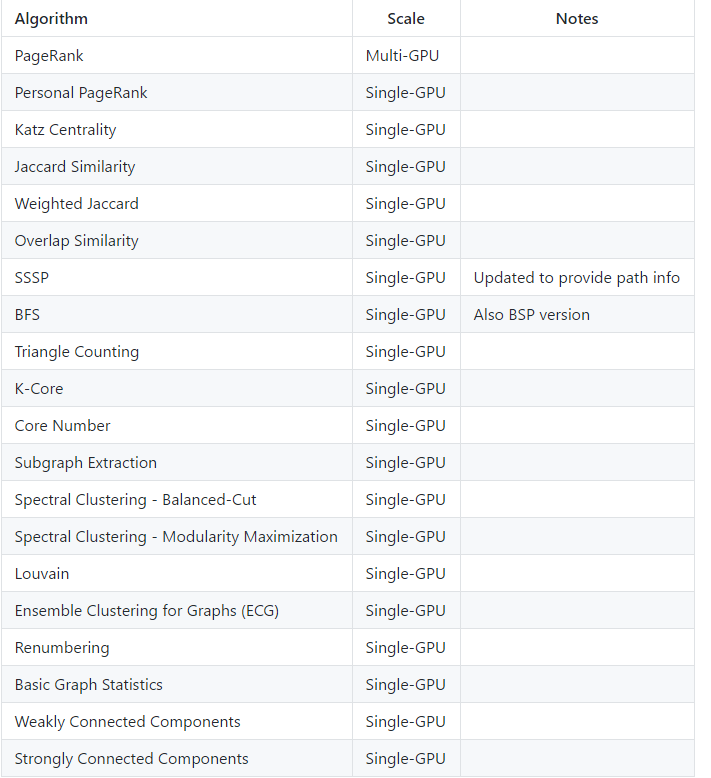
Supported models:

1 installation and background

1.1 installation

Conda installation, https://github.com/rapidsai/cugraph:

# CUDA 10.0
conda install -c nvidia -c rapidsai -c numba -c conda-forge -c defaults cugraph cudatoolkit=10.0

# CUDA 10.1
conda install -c nvidia -c rapidsai -c numba -c conda-forge -c defaults cugraph cudatoolkit=10.1

# CUDA 10.2
conda install -c nvidia -c rapidsai -c numba -c conda-forge -c defaults cugraph cudatoolkit=10.2

For docker version, please refer to: https://rapids.ai/start.html "prerequisites"

docker pull rapidsai/rapidsai:cuda10.1-runtime-ubuntu16.04-py3.7
docker run --gpus all --rm -it -p 8888:8888 -p 8787:8787 -p 8786:8786 \
    rapidsai/rapidsai:cuda10.1-runtime-ubuntu16.04-py3.7

1.2 background

cuGraph has taken a new step in integrating the leading graphics framework into an easy-to-use interface. A few months ago, RAPIDS received a copy of Hornet from the Georgia Institute of technology and reconstructed and renamed it cuHornet. This name change indicates that the source code has deviated from the Georgia Tech benchmark and reflects the matching of code API and data structure with RAPIDS cuGraph. The addition of cuHornet provides a boundary based programming model, a dynamic data structure and a list of existing analyses. In addition to the core number function, the first two available cuHornet algorithms are Katz centrality and K-Cores.

cuGraph is the graph analysis library of RAPIDS. Aiming at cuGraph, we propose a multi GPU PageRank algorithm supported by two new primitives: This is a multi GPU data converter from COO to CSR, and a function to calculate vertex degree. These primitives are used to convert source and target edge columns from Dask Dataframe to graphics format, and enable PageRank to scale across multiple GPUs.

The following figure shows the performance of the new multi GPU PageRank algorithm. Unlike the previous PageRank benchmark runtimes, these runtimes only measure the performance of the PageRank solver. This set of runtime includes Dask DataFrame to CSR transformation, PageRank execution, and result transformation from CSR back to DataFrame. The average results show that the new multi GPU PageRank analysis is more than 10 times faster than the 100 node Spark cluster.

Figure 1: time taken by cuGraph PageRank to calculate on different numbers of edges and NVIDIA Tesla V 100

The figure below only looks at the Bigdata dataset, 50 million vertices and 1.98 billion edges, and runs the HiBench end-to-end test. HiBench benchmark running time includes data reading, PageRank running, and then get the scores of all vertices. Previously, HiBench tested Google GCP on 10, 20, 50, and 100 nodes, respectively.

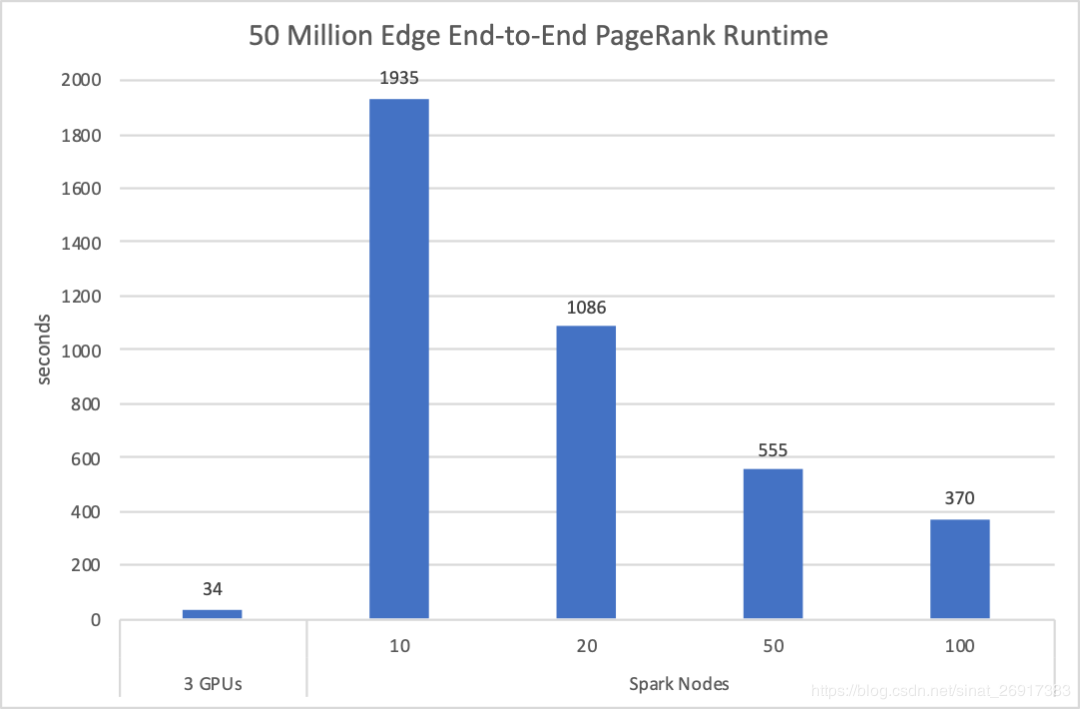
Figure 2: cuGraph PageRank vs Spark Graph (the lower the better) when 50 million edge to end PageRank is running

2 simple demo

Reference: https://github.com/rapidsai/cugraph

import cugraph

# assuming that data has been loaded into a cuDF (using read_csv) Dataframe
gdf = cudf.read_csv("graph_data.csv", names=["src", "dst"], dtype=["int32", "int32"] )

# create a Graph using the source (src) and destination (dst) vertex pairs the GDF  
G = cugraph.Graph()
G.add_edge_list(gdf, source='src', destination='dst')

# Call cugraph.pagerank to get the pagerank scores
gdf_page = cugraph.pagerank(G)

for i in range(len(gdf_page)):
	print("vertex " + str(gdf_page['vertex'][i]) + 
		" PageRank is " + str(gdf_page['pagerank'][i]))  

3 PageRank

cugraph.pagerank(G,alpha=0.85, max_iter=100, tol=1.0e-5)

• G: cugraph.Graph object
• alpha: float, The damping factor represents the probability to follow an outgoing edge. default is 0.85
• max_iter: int, The maximum number of iterations before an answer is returned. This can be used to limit the execution time and do an early exit before the solver reaches the convergence tolerance. If this value is lower or equal to 0 cuGraph will use the default value, which is 100
• tol: float, Set the tolerance the approximation, this parameter should be a small magnitude value. The lower the tolerance the better the approximation. If this value is 0.0f, cuGraph will use the default value which is 0.00001. Setting too small a tolerance can lead to non-convergence due to numerical roundoff. Usually values between 0.01 and 0.00001 are acceptable.

Returns:

• df: a cudf.DataFrame object with two columns:
  • df['vertex']: The vertex identifier for the vertex
  • df['pagerank']: The pagerank score for the vertex

Installation:

# The notebook compares cuGraph to NetworkX,  
# therefore there some additional non-RAPIDS python libraries need to be installed. 
# Please run this cell if you need the additional libraries
!pip install networkx
!pip install scipy

Code module:

# Import needed libraries
import cugraph
import cudf
from collections import OrderedDict


# NetworkX libraries
import networkx as nx
from scipy.io import mmread

# Related parameters

# define the parameters 
max_iter = 100  # The maximum number of iterations
tol = 0.00001   # tolerance
alpha = 0.85    # alpha
# Define the path to the test data  
datafile='../data/karate-data.csv'

# NetworkX
# Read the data, this also created a NetworkX Graph 
file = open(datafile, 'rb')
Gnx = nx.read_edgelist(file)

pr_nx = nx.pagerank(Gnx, alpha=alpha, max_iter=max_iter, tol=tol)

cuGraph model:

# cuGraph

# Read the data  
gdf = cudf.read_csv(datafile, names=["src", "dst"], delimiter='\t', dtype=["int32", "int32"] )

# create a Graph using the source (src) and destination (dst) vertex pairs from the Dataframe 
G = cugraph.Graph()
G.from_cudf_edgelist(gdf, source='src', destination='dst')


# Call cugraph.pagerank to get the pagerank scores
gdf_page = cugraph.pagerank(G)


# Find the most important vertex using the scores
# This methods should only be used for small graph
bestScore = gdf_page['pagerank'][0]
bestVert = gdf_page['vertex'][0]

for i in range(len(gdf_page)):
    if gdf_page['pagerank'][i] > bestScore:
        bestScore = gdf_page['pagerank'][i]
        bestVert = gdf_page['vertex'][i]
        
print("Best vertex is " + str(bestVert) + " with score of " + str(bestScore))

# A better way to do that would be to find the max and then use that values in a query
pr_max = gdf_page['pagerank'].max()


def print_pagerank_threshold(_df, t=0) :
    filtered = _df.query('pagerank >= @t')
    
    for i in range(len(filtered)):
        print("Best vertex is " + str(filtered['vertex'][i]) + 
            " with score of " + str(filtered['pagerank'][i]))              


print_pagerank_threshold(gdf_page, pr_max)
sort_pr = gdf_page.sort_values('pagerank', ascending=False)
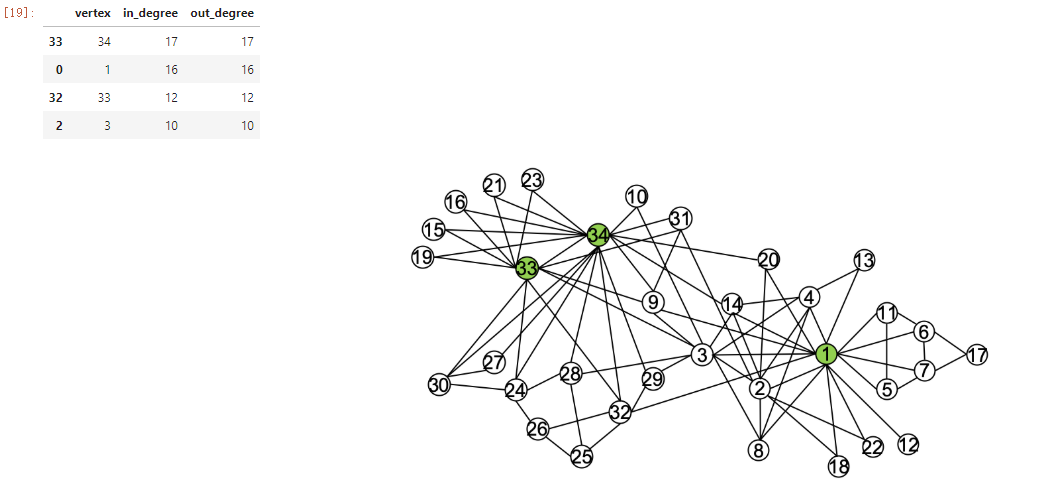
d = G.degrees()
d.sort_values('out_degree', ascending=False).head(4)

Association results: