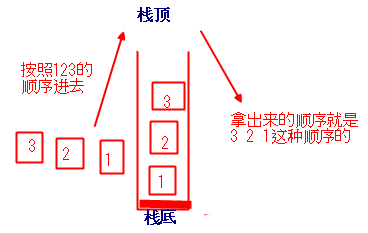
What is a Stack? The stack here and the java stack of the jvm are not one thing...

As a data structure, I feel that stack is like an interface. There are many ways to realize stack functions, such as using arrays, collections and linked lists. The most important feature of stack is to go first, then go out. You can imagine how to put the box of badminton into the badminton and take out the badminton. We call the action of putting badminton into the stack or putting it into the stack (p Ush), the action of pulling out badminton is called pop or pop.

In fact, there is already a stack implementation in java, which is Stack. Let's use it briefly.

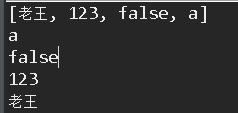
package com.wyq.thread;

import java.util.Stack;

public class MyStack {
    public static void main(String[] args) {
        Stack<Object> stack = new Stack<Object>();
        stack.push("Lao Wang");
        stack.push(123);
        stack.push(false);
        stack.push('a');
        System.out.println(stack.toString());
        
        for (int i = 0; i < 4; i++) {
            System.out.println(stack.pop());
        }
    }
}

This Stack is implemented by default using a collection, which inherits Vector, which is a collection that implements the List interface, and we also know that this Vector class is thread-safe, with synchronized keywords added to each method, so that means the efficiency will not be very high. We can try to use arrays to simply implement a stack by ourselves. Maybe we have a little understanding of the data structure of the stack. Why is the stack first-in-last-out? If we want to achieve how to achieve this way of access?

In the stack we implemented, I will not expand in real terms, because it is easy to confuse more logic, but I would like to explain the principle of expansion.

If there is a maximum capacity of 20 arrays A, there will also be a load factor of 0.75, what is the purpose of this load factor?

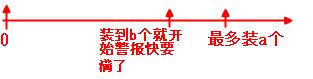
This 0.75 is derived from a/b. Although the value of 0.75 can be modified, it is said that 0.75 is the most stable value and it is best not to modify this value.

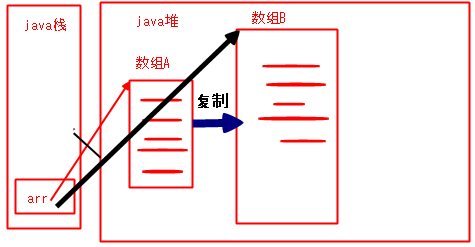
When we put the data in the A array, when we put 20*0.75=15 data, the array will receive an alarm, fill it up quickly, think about something quickly, so ah, create an array larger than 20, assuming that it is 40-capacity array B, then we copy all the data in the A array into the B array, and then modify the reference pointing to array A as follows The reference to array B is ok, as shown in the following figure:

For the sake of simplicity, the simpler the stack is, the better it is, we will not make these fancy things. How can we simply do this? The small partners who want to expand can add their own expansion methods.

By the way, the difference between +n and n+, --n and n--is like Value = ++n, which means n is assigned to value first + 1, then value = n++, which means n is assigned to value first, then n is assigned to value then + 1

package com.wyq.thread;

import java.util.Arrays;

public class MyStack {
    private Object[] arr;
    //Maximum capacity in an array
    private int maxlength;
    //The element pointing to the top of the stack, that is, the element pointing to the last position of the array
    private int top;
    
    //Invoke parametric constructs, default is 10 capacity arrays
    public MyStack(){
        this(10);
    }
    public MyStack(int len){
        this.maxlength = len;
        arr = new Object[maxlength];
        top = -1;//Because there was no data in the array at first, we put it in top=-1 Represents that there are no elements in an array
    }
    //Stack, first of all to ensure top The value should not be greater than the maximum index, otherwise the data will be put outside the array.
    //To drop a data into the stack, first drop it into the stack. top Move back and forth and put data in that position.
    public void push(Object obj){
        if (top<maxlength-1) {
            arr[++top] = obj;
            
        }
    }
    //Bullet stack, first find the element on the top of the stack, this peek()The method is right below, returning the top element of the stack, and then changing the last data of the array to null
    //Finally, we will top Move a position forward to make sure top Always point to the top element of the stack (the last element of the array)
    public Object pop(){
        Object peek = peek();
        arr[top--]=null;
        return peek;
    }
    //Look up the data on the top of the stack. Notice that there is no stack at this time. We just want to see what is on the top of the stack.
    public Object peek(){
        return arr[top];
    }
    //Rewrite toString Method to better display the data in the stack
    @Override
    public String toString() {
        return Arrays.toString(arr)+"]";
    }
    public static void main(String[] args) {
        MyStack stack = new MyStack();
        stack.push("Lao Wang");
        stack.push(123);
        stack.push(false);
        stack.push('a');
        System.out.println(stack.toString());
        
        for (int i = 0; i < 4; i++) {
            System.out.println(stack.pop());
        }
    }
}

It feels a lot easier than the array in the last article.