1. Ternary conditional operator
verilog has a ternary conditional operator (?:), just like C.
(condition ? if_true : if_false)
This can be used to select one of two values based on the condition on a line (multiplexer!) without using if then in the combined always block.
For example:
(0 ? 3 : 5) // This is 5 because the condition is false.
(sel ? b : a) // A 2-to-1 multiplexer between a and b selected by sel.
always @(posedge clk) // A T-flip-flop.
q <= toggle ? ~q : q;
always @(*) // State transition logic for a one-input FSM
case (state)
A: next = w ? B : A;
B: next = w ? A : B;
endcase
assign out = ena ? q : 1'bz; // A tri-state buffer
((sel[1:0] == 2'h0) ? a : // A 3-to-1 mux
(sel[1:0] == 2'h1) ? b :
c )
practice:
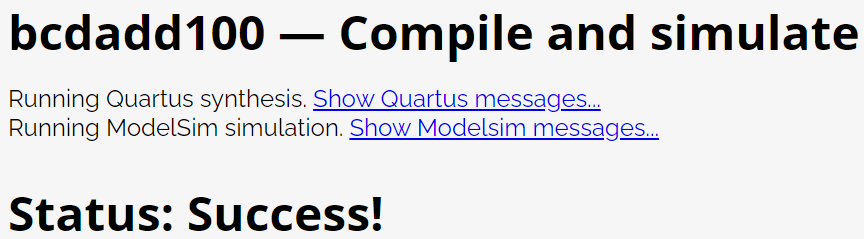
Given four unsigned numbers, find the minimum. Unsigned numbers can be compared with standard comparison operators (a < b). Use the conditional operator to create a two-way minimum circuit, and then combine some of them to create a four-way minimum circuit. You may need some vectors for intermediate results.
Code implementation:
module top_module (
input [7:0] a, b, c, d,
output [7:0] min);
wire [7:0]min1,min2;
assign min1 = (a > b)? b : a;
assign min2 = (c > d)? d : c;
assign min = (min1 > min2)? min2 : min1;
endmodule
Verification results:
2. Reduction operator
You are already familiar with bitwise operations between two values, such as a & B or a ^ b. Sometimes, you want to create a wide gate and operate all bits of a vector, such as (a [0] & A [1] & A [2] & A [3]...). If the vector is very long, it will become very boring.
The reduction operator can perform "and", "or" and "XOR" operations on the bits of the vector to produce a bit output.
& a[3:0] // AND: a[3]&a[2]&a[1]&a[0]. Equivalent to (a[3:0] == 4'hf) | b[3:0] // OR: b[3]|b[2]|b[1]|b[0]. Equivalent to (b[3:0] != 4'h0) ^ c[2:0] // XOR: c[2]^c[1]^c[0]
These are unary operators with only one operand (similar to the NOT operators! And ~).
You can also reverse the output of these gates to create NAND, NOR and XNOR gates, for example (~& d [7:0]).
practice:
Parity is often used as a simple method to detect errors when transmitting data over imperfect channels. Create a circuit that will calculate an 8-bit byte parity bit (the 9th bit byte will be added). We will use "even" parity, where the parity bit is the exclusive or of all 8 data bits.
Code implementation:
module top_module (
input [7:0] in,
output parity);
assign parity = ^ in;
endmodule
Verification results:
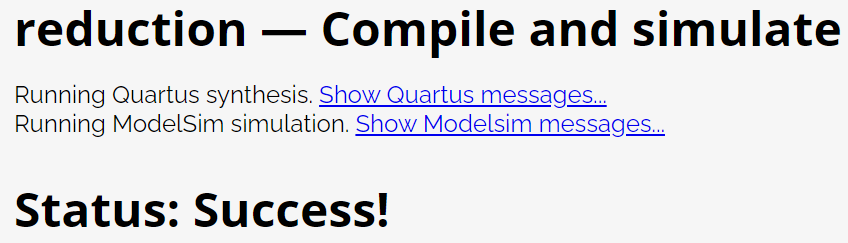
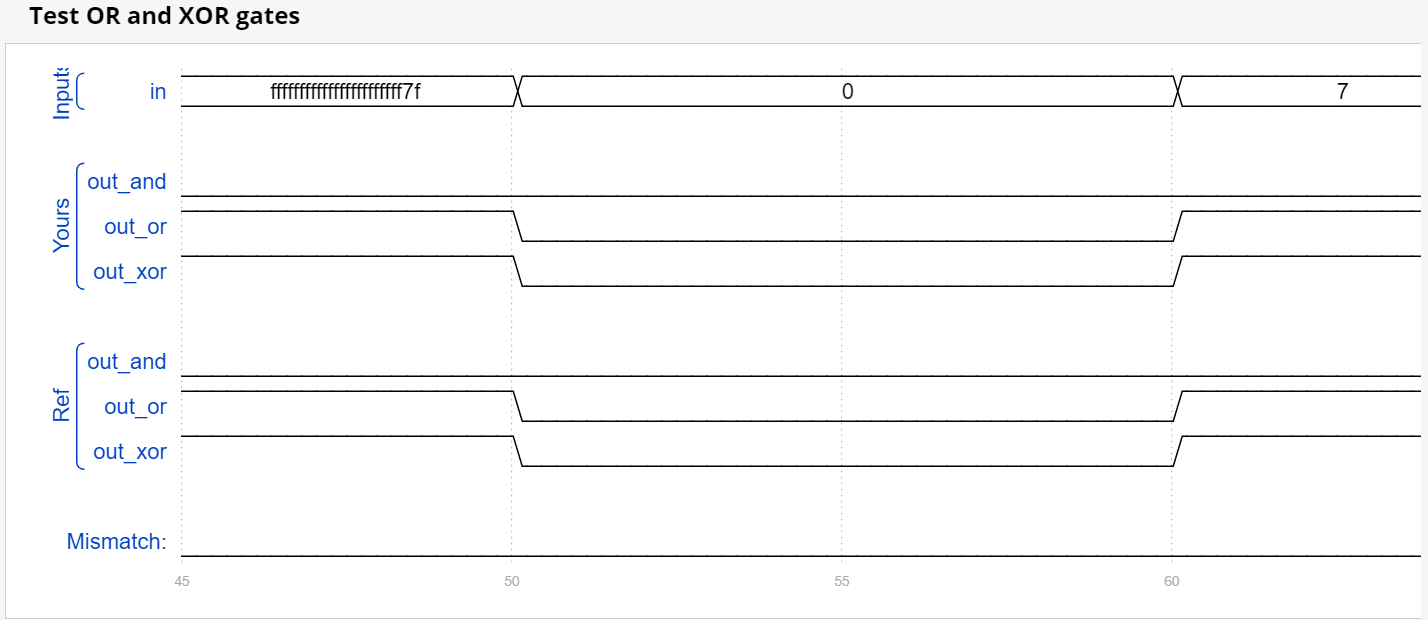
3. Reduction: wider door
Establish a combinational circuit with 100 inputs in [99:0].
There are 3 outputs:
①out_and: 100 input and gate output.
②out_or: 100 input OR gate output.
③out_xor: 100 input the output of XOR gate.
Code implementation:
module top_module(
input [99:0] in,
output out_and,
output out_or,
output out_xor
);
assign out_and = & in;
assign out_or = | in;
assign out_xor = ^ in;
endmodule
Verification results:
4. Combined for loop: vector inversion 2
Given a 100 bit input vector [99:0], reverse its bit order.
Code implementation:
module top_module(
input [99:0] in,
output [99:0] out
);
integer i;
always@(*) begin
for( i = 0 ;i <= 99;i = i + 1 ) begin
out[i] = in[99-i];
end
end
endmodule
Verification results:
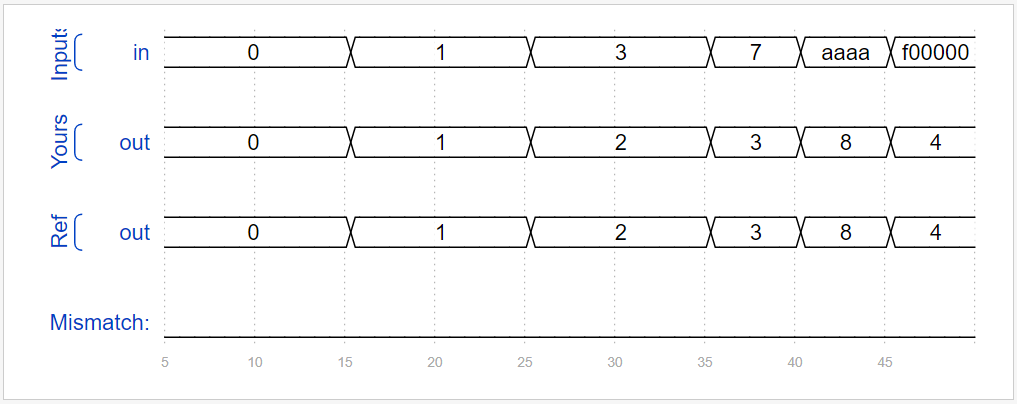
5. Combined for loop: 255 bit total count
The "total count" circuit calculates the number of "1" in the input vector. Construct the overall counting circuit for the 255 bit input vector.
Code implementation:
module top_module(
input [254:0] in,
output [7:0] out );
integer i;
always@(*) begin
out = 8'b0;
for(i = 0;i <= 254;i = i + 1) begin
out = out + in[i];
end
end
endmodule
Verification results:
6. Generate for loop: 100 bit binary adder 2
Create a 100 bit binary traveling wave carry adder by instantiating 100 full adders. The adder adds two 100 bit numbers and a carry to produce a 100 bit sum and carry. To encourage you to actually instantiate the full adder, you also output the carry of each full adder in the traveling wave carry adder. cout[99] is the last carry of the last full adder, which you often see.
expand:
generate syntax
(1) Define genvar as the loop variable of generate.
(2) The for statement defined in the generate statement must have a begin to prepare for subsequent label addition.
begin must have a name, that is, it must have a label, because the label will be used as the instance name of the generate loop.
(3) The types that can be used in generate statements are:
① module
② UDP (user defined primitive)
③ Gate level primitive
④ Continuous assignment statement
⑤ initial or always statement
The basic structure of generate is as follows:
genvar Loop variable name;
generate
// generate loop statement
// generate conditional statement
// generate branch statement
// Nested generate statement
endgenerate
Code implementation:
module top_module(
input [99:0] a, b,
input cin,
output [99:0] cout,
output [99:0] sum );
genvar i;
generate
for( i = 0 ; i < 100; i = i + 1 )
begin:adder
if(i==0)
begin
assign {cout[i],sum[i]} = a[i] + b[i] + cin;
end
else
begin
assign {cout[i],sum[i]} = a[i] + b[i] + cout[i-1];
end
end
endgenerate
endmodule
Verification results:
7. Generate for loop: 100 bit BCD adder
Provides you with a file called bcd_fadd's BCD one digit adder, which adds the sum and carry of two BCD numbers to produce a sum and carry.
module bcd_fadd (
input [3:0] a,
input [3:0] b,
input cin,
output cout,
output [3:0] sum );
Instantiate 100 bcds_ FADD copy to create a 100 bit BCD traveling wave carry adder. Your adder should add two 100 bit BCD numbers (packed into a 400 bit vector) and a carry to produce a 100 bit sum and operate.
Code implementation:
module top_module(
input [399:0] a, b,
input cin,
output cout,
output [399:0] sum );
wire [99:0]cout1;
genvar i;
generate
for( i = 0 ; i < 100; i = i + 1 )
begin:adder
if(i==0)
bcd_fadd U0( .a(a[3:0]), .b(b[3:0]), .cin(cin), .cout(cout1[0]), .sum(sum[3:0]));
else
bcd_fadd U1( .a(a[4*i+3:4*i]), .b(b[4*i+3:4*i]), .cin(cout1[i-1]), .cout(cout1[i]), .sum(sum[4*i+3:4*i]));
end
assign cout = cout1[99];
endgenerate
endmodule
Verification results: