Start with this blog and slowly learn about Map collections together
What is Map?
Map is different from List.
In List, we remember that it is mainly a linear list, which can be subdivided into Array List, Vector, and LinkedList. ) And the main thing is that List has only value, that is, only one value.
In Map, it stores a combination of key-value pairs, that is, key-value. The basic operation is to act on this combination.
Look at the implementation of Map interface:
public interface Map<K,V>There are many ways to construct Map. This paper mainly introduces the implementation of TreeMap based on red-black tree.
Basic Characteristics of TreeMap
First look at the definition:
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable1: Orderliness
Navigable Map is a collection of extended SortedMap s, so TreeMap is also ordered. Note that the orderliness here is different from that in ArrayList.
It's like 10 children standing in line.
In Array List, enter in turn. I can't guarantee that it will be sorted in order of height, but it must be in order, that is, if Zhang San enters in front of Li Si.
Wang Wu enters behind Li Si, so in the final queue, Li Si must be Zhang San and Wang Wu (of course, the relationship of orientation can also be Wang Wu and Zhang San).
In TreeMap, because of the different structure, it is not a linear table, but through iterator traversal (comparator determined by height), it can ensure that the final output is in the order of height.
So they are different.
2: Null Value Problem of Element Value
From the analysis of the above characteristics, TreeMap is ordered, but in fact it is compared by Comparator, so that it can be ordered. When creating a TreeMap, you can pass in Comparator auxiliary sorting, or use the default Comparator to determine the size (forcibly compared with the parent class Comparator). What's the intention, that is, you can set the key to null if you want to pass a Comparator by yourself, considering null. Of course, the value can also be null, normal output.
First look at the source code for the value obtained:
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
//By default, key is not allowed to be null
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
//When you use your own Comparator
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator<? super K> cpr = comparator;
if (cpr != null) {
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}3: No duplication allowed
When a new value is inserted, it will be searched downward along the binary tree until the appropriate location is found. If the key s are equal, replacement operations will occur. Therefore, repetition is not allowed. The specific principle will be analyzed in the following section.
4): Time complexity of operations
In the description of jdk, it is pointed out that the time complexity of log(n) in get, put, remove and other operation methods is O (log n) in average and worst case. It can be seen in the following specific analysis.
5: Non-thread security
TreeMap is non-thread-safe. When using it, pay attention to synchronization or use wrapper classes to synchronize.
synchronizedSortedMap Collections.synchronizedSortedMap
The Principle of TreeMap
TreeMap is based on binary tree. You can see some articles on the Internet without knowing binary tree. There are many kinds of trees in the binary tree. One kind of tree is called AVL. Here you can see: AVL . In the concrete implementation of AVL tree, there is another typical implementation method, which is red-black tree. red-black tree .
In Java, TreeMap is based on this red-black tree.
Perhaps here, there are still many readers will be very confused, do not understand what TreeMap is. Here we introduce the basic characteristics of red-black trees, and finally give a simple and easy-to-understand principle of TreeMap.
red-black tree
Binary search tree
Because the red-black tree is essentially a binary search tree, before we understand the red-black tree, let's first look at the binary search tree.
Binary Search Tree, also known as ordered binary tree, sorted binary tree, refers to an empty tree or a binary tree with the following properties:
- If the left subtree of any node is not empty, the value of all nodes in the left subtree is less than that of its root node. - If the right subtree of any node is not empty, the values of all nodes in the right subtree are greater than those of its root node. - The left and right subtrees of any node are also binary search trees. - There are no duplicate nodes with equal keys.
Because a random binary search tree with n nodes is LGN in height, it is logical that the execution time of general operations is O (lgn).
However, if a binary tree degenerates into a linear chain with n nodes, the worst-case running time of these operations is O (n), that is, a programming slant. Later we will see a binary search tree-red-black tree, which makes the tree relatively balanced through some properties, so that the time complexity of the final search, insertion and deletion is still O (lgn) in the worst case.
red-black tree
And the red and black tree is also a binary tree.
But how does it ensure that the height of a red-black tree with n nodes remains at h = logn all the time? This leads to five properties of red-black trees:
1) Each node is either red or black. 2) The root node is black. 3) Each leaf node (leaf node refers to the NIL pointer or NULL node at the end of the tree) is black. 4) If a node is red, then both of its sons are black. 5) For any node, each path to the NIL pointer at the end of the leaf node tree contains the same number of black nodes.
It is precisely these five properties that ensure the height of the red-black tree to be log (n), so the time complexity of searching, inserting and deleting is the worst for O(log n).
When will these five new values be used? When you change the structure of the tree (insert, delete), you need to adjust to ensure that these five properties change.
After that, it was a red and black tree.
Let's look at a graph first to see: (that is, balanced binary tree, with red and black color node restrictions) 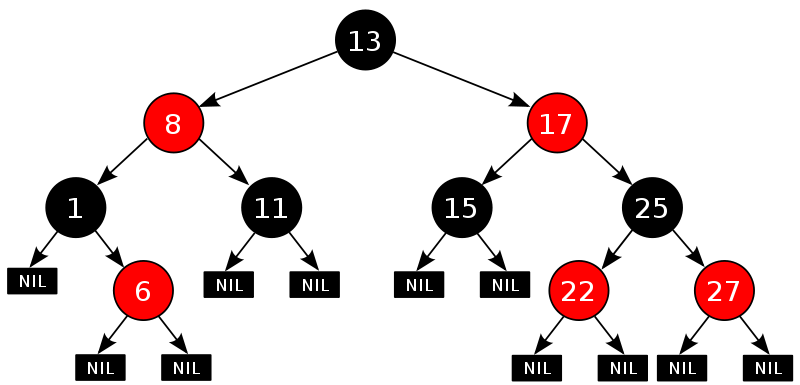
Knowledge of tree rotation
It mainly includes left-handed and right-handed. In the balanced binary tree, the maximum height difference used to adjust the binary tree does not exceed 1.
Left handed: 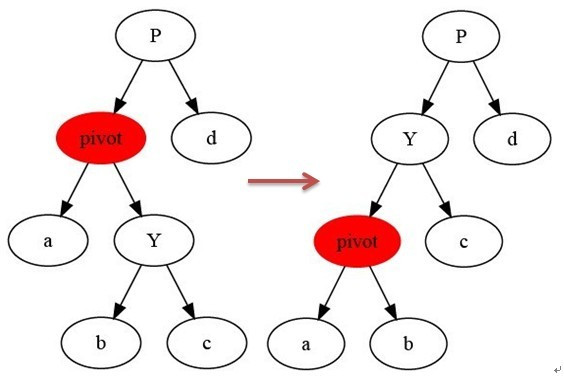
Dextral: 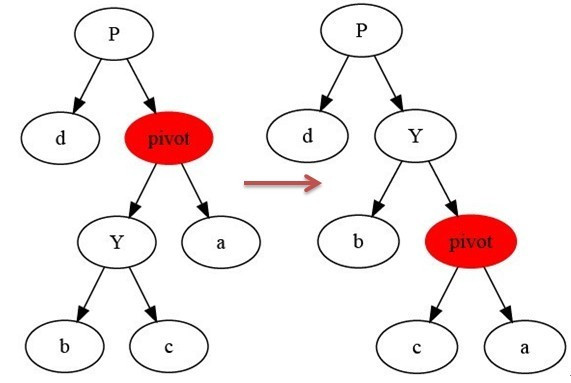
Insertion and adjustment
Next is the insertion process of the red-black tree.
The first step is to determine where the new node is suitable for placement. The step is to traverse downward from the root node, small left and large right.
When found, the value is inserted, but after the insertion process, the structure and related properties of the tree will change, leading to no longer conform to the characteristics of the red-black tree, which needs to be adjusted.
After adjusting the steps, the structure of the tree once again conforms to the characteristics of the red-black tree, and the values are interpolated.
This article focuses on TreeMap in Java. Of course, after understanding the red-black tree, you can easily understand TreeMap and understand accessibility in depth.
julycoding
Delete and adjust
As with the insertion step, let's not go into details.
First find the node, then delete the node, adjust.
Omnibus
Red-black tree is a balanced binary tree. Its red-black structure guarantees the balance of the tree and ensures the efficiency of insertion, deletion and search, i.e. log(n). So every time a node is inserted, it is adjusted to ensure the red-black structure of the tree.
TreeMap Source Code Analysis
Here, the specific action method of TreeMap is introduced.
Input an ordered set for construction
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
//Create a treemap from an ordered set
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
/**
* Get data from an ordered set and insert it.
* Attention is orderly
*/
private void buildFromSorted(int size, Iterator<?> it,
java.io.ObjectInputStream str,
V defaultVal)
throws java.io.IOException, ClassNotFoundException {
this.size = size;
root = buildFromSorted(0, 0, size-1, computeRedLevel(size),
it, str, defaultVal);
}
/**
* Insert operation
*
* level : Layers that the current node should insert
* lo: The first node of the subtree
* hi: The last node of the subtree
* @param Indicates that the node in this layer must be red
*/
@SuppressWarnings("unchecked")
private final Entry<K,V> buildFromSorted(int level, int lo, int hi,
int redLevel,
Iterator<?> it,
java.io.ObjectInputStream str,
V defaultVal)
throws java.io.IOException, ClassNotFoundException {
//Judging whether there is a mistake
if (hi < lo) return null;
int mid = (lo + hi) >>> 1;
Entry<K,V> left = null;
//Go down and recursively find the left child node
if (lo < mid)
left = buildFromSorted(level+1, lo, mid - 1, redLevel,
it, str, defaultVal);
//Find the process of setting values.
K key;
V value;
if (it != null) {
if (defaultVal==null) {
Map.Entry<?,?> entry = (Map.Entry<?,?>)it.next();
key = (K)entry.getKey();
value = (V)entry.getValue();
} else {
key = (K)it.next();
value = defaultVal;
}
} else { // use stream
key = (K) str.readObject();
value = (defaultVal != null ? defaultVal : (V) str.readObject());
}
Entry<K,V> middle = new Entry<>(key, value, null);
// After setting it up, you start setting color and connecting the node to the parent and child nodes where you want to insert them.
if (level == redLevel)
middle.color = RED;
if (left != null) {
middle.left = left;
left.parent = middle;
}
if (mid < hi) {
//Recursive way to get the next lower right byte point
Entry<K,V> right = buildFromSorted(level+1, mid+1, hi, redLevel,
it, str, defaultVal);
middle.right = right;
right.parent = middle;
}
return middle;
}The above code constructs a TreeMap by passing in an ordered set. Because it is an ordered set, it must be constructed from both ends of the binary tree.
getEntry method
That is, through a key, the node to which the key belongs is obtained.
/**
* Looking for key from an entity defaults to no comparator.
* Use the default compareTo for comparison.
*
* Thus, key cannot be null.
*/
final Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}The getEntry method only deals with the search of binary trees, so it does not involve adjustment, that is, searching downward from the root node. This code lists whether the key is null or not.
In TreeMap with binary tree structure, values are not always found, so there are many get methods in TreeMap, such as:
final Entry
/**
* The ceiling, so it's on top, so it's the smallest one larger than k.
* Find a node larger than key, the smallest node, which can be equal to k, and get the smallest node in TreeMap that is not less than key.
If it does not exist (that is, all nodes in TreeMap have keys larger than keys), return null
* @param key
* @return
*/
final Entry<K,V> getCeilingEntry(K key) {
Entry<K,V> p = root;
while (p != null) {
int cmp = compare(key, p.key);
// Case 1: If "key of p" is > key.
// If there is a left child in p, let p= "the left child in p";
// Otherwise, return p
if (cmp < 0) {
if (p.left != null)
p = p.left;
else
return p;
// Situation 2: If "key of p" is less than key.
} else if (cmp > 0) {
// If P has a right child, let p= "the right child of p"
if (p.right != null) {
p = p.right;
} else {
// If p does not have a right child, find the successor node of p and return
// Note: There are two possibilities for the "p successor node" returned here: first, null; and second, the smallest node larger than key in TreeMap.
// The key to understanding this is that getCeilingEntry traverses from root.
// If getCeiling Entry can go this far, then the "key of the node that has been traversed" before it is all > key.
// If you can understand the above, it's easy to understand why there are two possibilities for "p's successor node".
Entry<K,V> parent = p.parent;
Entry<K,V> ch = p;
while (parent != null && ch == parent.right) {
ch = parent;
parent = parent.parent;
}
return parent;
}
// Case 3: If "key of p" equals key.
} else
return p;
}
return null;
} put method
put method step, first down to find the most suitable place for this (key, value) pair, then insert, and finally adjust
/**
* Insert a pair of key value pairs k and v into treemap. If k already exists, replacement will occur and value will replace old value.
*/
public V put(K key, V value) {
Entry<K,V> t = root;
if (t == null) {
//Check for null
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
// Right and left two lines, down search
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//Finding the Best Place
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//Adjustment after insertion
fixAfterInsertion(e);
size++;
modCount++;
return null;
}delete method
Compared with the put method, the delete method does not need to find the node any more, because it has already given you the node. Of course, some methods need to find the node if they only provide the key.
/**
* Delete p, then rebalance
*/
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// p has two child nodes
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
// Select an alternative node that will be deleted
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else {
if (p.color == BLACK)
//Adjustment after deletion
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}Iterator in TreeMap
First, the Iterator in TreeMap is also fail-fast. One thing to note here is that in Map collections, traversal operations can only be implemented through Iterator, because Map is not a linear table, so you can't traverse all operations with a for loop like Array List.
There are several different implementations of Iterator in TreeMap
Static class TreeMapSpliterator < K, V>: As the parent class of the following two Iterators in the Iterator of TreeMap, implements the common pliterator method.
Static final class KeySpliterator < K, V >: key's split iterator.
Static final class Descending KeySpliterator < K, V>: A split iterator for an inverted key.
The pictures in this article and the mangrove tree learning are cited as follows:
julycoding