1, Brief introduction of bloon filter

Last time, we learned to use HyperLogLog to estimate big data. It is very valuable and can solve many statistical requirements with low accuracy. But if we want to know whether a certain value is already in the HyperLogLog structure, it can't help. It only provides pfadd and pfcount methods, but no methods like contains.

Tiktok: let's take a scenario.

 

Do you have repeated recommendations? So many recommended content should be recommended to so many users. How can it ensure that when each user views the recommended content, they will not see the recommended video that they have seen before? That is to say, how to achieve tiktok?

You will think that the server records all the historical records that users have seen. When the recommendation system recommends short videos, it will filter out the existing records from each user's historical records. The question is, when the number of users is large and each user has seen a lot of short videos, does the de duplication of recommendation system keep up with the performance in this way?

In fact, if the history records are stored in the relational database, the database needs to be frequently queried for exists to remove duplicates. When the system concurrency is very high, the database is difficult to resist the pressure.

 

You may think of caching again, but if so many users have so many history records, how much space will be wasted if they are all cached. (maybe the boss will take a look at the bill and you...) and the storage space will grow linearly with time. Even if you can last for a month with caching, how long will it last? No cache performance and can not keep up, what to do?

As shown in the figure above, bloom filter is such a high-level data structure specially used to solve the problem of de duplication. But like HyperLogLog, it is also a little bit inaccurate, and there is a certain probability of miscalculation, but it can save more than 90% in space while solving the problem of de duplication, which is also very worthwhile.

What is a bloon filter

Bloom Filter was proposed by bloom in 1970. It is actually a very long binary vector and a series of random mapping functions (to be detailed below). In fact, you can simply understand it as a less precise set structure. When you use its contains method to determine whether an object exists, it may misjudge. But the Bloom Filter is not particularly imprecise. As long as the parameters are set reasonably, its accuracy can be controlled relatively accurately, and there will only be a small probability of misjudgment.

When the bloom filter says a value exists, it may not exist; when it says no, it must not exist. For example, when it says that it doesn't know you, it's true that it doesn't know you, but when it says that it knows you, it may be because you look like another friend it knows (with a similar face), so it misjudges you.

Use scenario of bloon filter

Based on the above functions, we can roughly use the bloom filter in the following scenarios:

• Determine whether big data exists: this can achieve the above de duplication function. If your server memory is large enough, then using HashMap may be a good solution. In theory, the time complexity can reach the level of O(1), but when the data volume is up, only the bloom filter can be considered.

• Solve cache penetration: we often put some hot data in Redis as cache, such as product details. Generally, after a request comes, we will query the cache first instead of reading the database directly. This is the simplest and most common way to improve performance. However, if we always request a cache that does not exist, then there must be no cache at this time. Then a large number of requests will be directly hit the database, causing cache penetration. The bloom filter can also be used to solve this problem Such problems.

• Filtering of Crawler / mailbox system: usually I don't know if you have noticed that some normal mail will also be put into the spam directory, which is caused by misjudgment using the bloom filter.

2, Analysis of the principle of bloon filter

The bloom filter is essentially composed of a bit vector or a bit list with a length of m (only a list containing 0 or 1 bit values). Initially, all values are set to 0, so let's create a bit vector with a slightly longer length for presentation:

When we add data to the bloom filter, we will use multiple hash functions to calculate the key, get a certificate index value, and then modular the length of the bit array to get a location. Each hash function will calculate a different location. Then set these positions of the digit group to 1 to complete the add operation. For example, we add a wmyskxz:

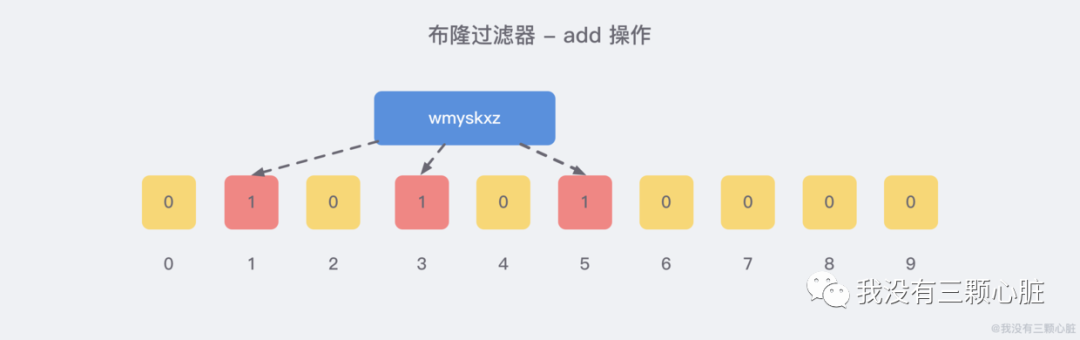
When querying the existence of the key from the bloom filter, as with the add operation, the key will be operated through the same multiple hash functions to check whether the corresponding positions are all 1. If one bit is 0, then the key in the bloom filter does not exist. If these positions are all 1, it doesn't mean that the key must exist. It can only be said that it is very likely to exist, because the 1 of these positions may be caused by the existence of other keys.

For example, after we add some data, we query a key that does not exist

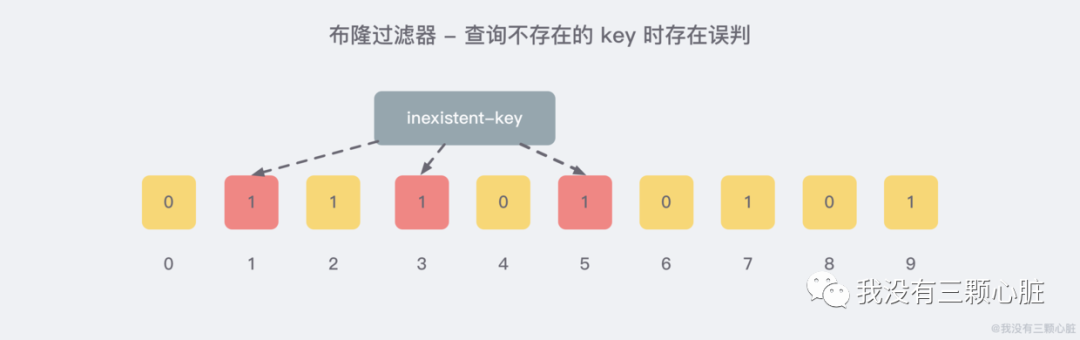
Obviously, 1 / 3 / 5 of these positions is caused by wmyskxz added for the first time, so there is a miscalculation here. Fortunately, bron filter has a formula that can predict the error rate. It's more complex. Interested friends can read it by themselves and burn their brains. Just remember the following points:

• When using, do not make the actual number of elements far greater than the number of initializations;

• When the actual number of elements exceeds the initial number, the bloon filter should be rebuilt, a larger size filter should be reassigned, and then all historical elements should be add ed in batches;

3, Use of bloon filter

The bron filter provided by Redis officially arrived at Redis 4.0 after it provided plug-in function. As a plug-in, the bloom filter is loaded into Redis Server, providing Redis with powerful bloom de duplication function. Now let's experience Redis 4.0's bloon filter. In order to save the tedious installation process, let's use Docker directly.

> docker pull redislabs/rebloom # Pull mirror image
> docker run -p6379:6379 redislabs/rebloom # Running container
> redis-cli # Connect the redis service in the container

If the execution of the above three instructions is OK, then you can experience the bloon filter.

• Of course, if you don't want to use Docker, you can also install the plug-in by yourself after checking the Redis version of this machine is qualified. Please refer to https://blog.csdn.net/u013030276/article/details/88350641 here

Basic usage of bloon filter

The bloom filter has two basic instructions, bf.add add element and bf.exists to query whether the element exists. Its usage is similar to sadd and sismember of set set set. Note that bf.add can only add one element at a time. If you want to add more than one element at a time, you need to use the bf.madd instruction. Similarly, if you need to query the existence of multiple elements at a time, you need to use the bf.exists instruction.

127.0.0.1:6379> bf.add codehole user1
(integer) 1
127.0.0.1:6379> bf.add codehole user2
(integer) 1
127.0.0.1:6379> bf.add codehole user3
(integer) 1
127.0.0.1:6379> bf.exists codehole user1
(integer) 1
127.0.0.1:6379> bf.exists codehole user2
(integer) 1
127.0.0.1:6379> bf.exists codehole user3
(integer) 1
127.0.0.1:6379> bf.exists codehole user4
(integer) 0
127.0.0.1:6379> bf.madd codehole user4 user5 user6
1) (integer) 1
2) (integer) 1
3) (integer) 1
127.0.0.1:6379> bf.mexists codehole user4 user5 user6 user7
1) (integer) 1
2) (integer) 1
3) (integer) 1
4) (integer) 0

The Blount filter used above is the default parameter of Blount filter, which is automatically created when we first add. Redis also provides a Boolean filter that can customize parameters. You only need to explicitly create it with the bf.reserve instruction before add. If the corresponding key already exists, bf.reserve will report an error.

bf.reserve has three parameters: key, error rate and initial size

• The lower the error rate is, the larger the space is needed. It doesn't matter if the settings are a little larger for occasions that don't need to be too precise. For example, the push system mentioned above will only filter a small part of the content, and the overall viewing experience will not be greatly affected;

• initial_size indicates the expected number of elements to be put in. When the actual number exceeds this value, the miscalculation rate will increase. Therefore, a large value should be set in advance to avoid the miscalculation rate rising due to the excess;

If bf.reserve is not applicable, the default error rate is 0.01 and the default initial size is 100.

4, Code implementation of bloon filter

Simple simulation implementation

According to the above basic theory, we can easily implement a data structure of the bloom filter for simple simulation by ourselves:

public static class BloomFilter {

    private byte[] data;

    public BloomFilter(int initSize) {
        this.data = new byte[initSize * 2]; // Default create space of size * 2
    }

    public void add(int key) {
        int location1 = Math.abs(hash1(key) % data.length);
        int location2 = Math.abs(hash2(key) % data.length);
        int location3 = Math.abs(hash3(key) % data.length);

        data[location1] = data[location2] = data[location3] = 1;
    }

    public boolean contains(int key) {
        int location1 = Math.abs(hash1(key) % data.length);
        int location2 = Math.abs(hash2(key) % data.length);
        int location3 = Math.abs(hash3(key) % data.length);

        return data[location1] * data[location2] * data[location3] == 1;
    }

    private int hash1(Integer key) {
        return key.hashCode();
    }

    private int hash2(Integer key) {
        int hashCode = key.hashCode();
        return hashCode ^ (hashCode >>> 3);
    }

    private int hash3(Integer key) {
        int hashCode = key.hashCode();
        return hashCode ^ (hashCode >>> 16);
    }
}

It's very simple here. Only a data array of byte type is maintained internally. In fact, byte still occupies as much as one byte, which can be optimized to bit instead. Here, it's just for the convenience of simulation. In addition, I also created three different hash functions. In fact, I refer to the HashMap hash jitter method and use the results of different or different bits of hash and right shift respectively. The basic methods of add and contains are provided.

Let's briefly test the effect of this bloom filter:

public static void main(String[] args) {
    Random random = new Random();
    // Let's say our data is 1 million
    int size = 1_000_000;
    // Use a data structure to save all the actual values
    LinkedList<Integer> existentNumbers = new LinkedList<>();
    BloomFilter bloomFilter = new BloomFilter(size);

    for (int i = 0; i < size; i++) {
        int randomKey = random.nextInt();
        existentNumbers.add(randomKey);
        bloomFilter.add(randomKey);
    }

    // Verify that all existing numbers exist
    AtomicInteger count = new AtomicInteger();
    AtomicInteger finalCount = count;
    existentNumbers.forEach(number -> {
        if (bloomFilter.contains(number)) {
            finalCount.incrementAndGet();
        }
    });
    System.out.printf("Actual data volume:%d, Judge the amount of data: %d \n", size, count.get());

    // Verify 10 nonexistent numbers
    count = new AtomicInteger();
    while (count.get() < 10) {
        int key = random.nextInt();
        if (existentNumbers.contains(key)) {
            continue;
        } else {
            // This must be a nonexistent number
            System.out.println(bloomFilter.contains(key));
            count.incrementAndGet();
        }
    }
}

The output is as follows:

Actual data volume: 1000000, Judge the amount of data: 1000000
false
true
false
true
true
true
false
false
true
false

This is what we mentioned earlier. When the bloom filter says that a certain value exists, the value may not exist. When it says that a certain value does not exist, it must not exist, and there is a certain miscalculation rate

Manual implementation reference

Of course, the above version is very low, but the main idea is not bad. Here is also a better version for your own implementation test reference:

import java.util.BitSet;

public class MyBloomFilter {

    /**
     * Size of digit group
     */
    private static final int DEFAULT_SIZE = 2 << 24;
    /**
     * With this array, you can create six different hash functions
     */
    private static final int[] SEEDS = new int[]{3, 13, 46, 71, 91, 134};

    /**
     * Digit group. Elements in an array can only be 0 or 1
     */
    private BitSet bits = new BitSet(DEFAULT_SIZE);

    /**
     * An array of classes containing hash functions
     */
    private SimpleHash[] func = new SimpleHash[SEEDS.length];

    /**
     * Initializes an array of classes containing hash functions. The hash functions in each class are different
     */
    public MyBloomFilter() {
        // Initializing multiple different Hash functions
        for (int i = 0; i < SEEDS.length; i++) {
            func[i] = new SimpleHash(DEFAULT_SIZE, SEEDS[i]);
        }
    }

    /**
     * Add element to digit group
     */
    public void add(Object value) {
        for (SimpleHash f : func) {
            bits.set(f.hash(value), true);
        }
    }

    /**
     * Determine whether the specified element exists in the bit array
     */
    public boolean contains(Object value) {
        boolean ret = true;
        for (SimpleHash f : func) {
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }

    /**
     * Static inner class. For hash operation!
     */
    public static class SimpleHash {

        private int cap;
        private int seed;

        public SimpleHash(int cap, int seed) {
            this.cap = cap;
            this.seed = seed;
        }

        /**
         * Calculate hash value
         */
        public int hash(Object value) {
            int h;
            return (value == null) ? 0 : Math.abs(seed * (cap - 1) & ((h = value.hashCode()) ^ (h >>> 16)));
        }

    }
}

Use the built-in bloon filter in Google's open source Guava

The main purpose of our own implementation is to make ourselves understand the principle of the bloom filter. The implementation of the bloom filter in Guava is relatively authoritative, so we don't need to manually implement a bloom filter in the actual project.

First, we need to introduce the dependency of Guava into the project:

<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>28.0-jre</version>
</dependency>

The actual use is as follows:

We have created a Boolean filter that can hold up to 1500 integers, and we can tolerate a probability of miscalculation of (0.01)

// Create a bloom filter object
BloomFilter<Integer> filter = BloomFilter.create(
        Funnels.integerFunnel(),
        1500,
        0.01);
// Determine whether the specified element exists
System.out.println(filter.mightContain(1));
System.out.println(filter.mightContain(2));
// Add elements to the bloom filter
filter.put(1);
filter.put(2);
System.out.println(filter.mightContain(1));
System.out.println(filter.mightContain(2));

In our example, when the mightcontent() method returns true, we can 99% determine that the element is in the filter, and when the filter returns false, we can 100% determine that the element does not exist in the filter.

The implementation of the Bulong filter provided by Guava is very good (you can see its source code implementation if you want to know more about it), but it has a major defect that it can only be used by a single machine (in addition, capacity expansion is not easy), and now the Internet is generally a distributed scenario. To solve this problem, we need to use the bloom filter in Redis.

Source: I don't have three hearts