Article catalog
Author: LSS has a long way to go
HashMap
preface
Before I introduce HashMap, I need to know something else: red black tree.
What is a red black tree
Red black tree is actually a self balanced binary search tree. The height of its left and right subtrees may be greater than 1. Strictly speaking, the red black tree is not a completely balanced binary tree. Then another question is introduced: what is a binary search tree? What are the disadvantages of binary search tree? Why do red and black trees grow?
Here is a link: https://www.cs.usfca.edu/~galles/visualization/Algorithms.html You can clearly see the process of inserting, deleting and taking values of various data structures.
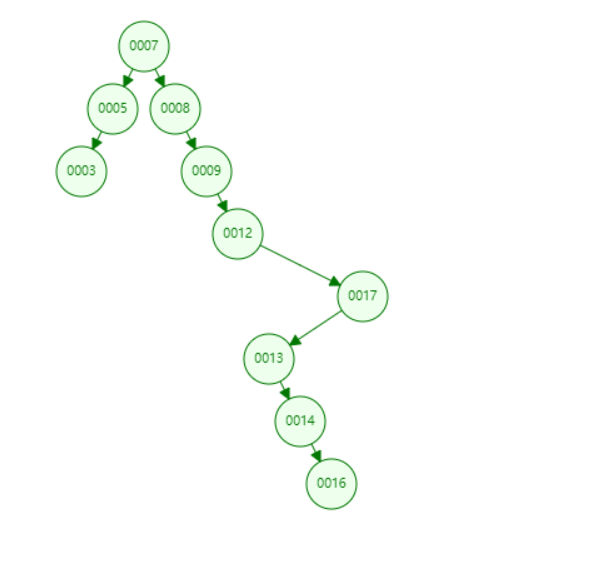
As shown in the figure: This is the real column of a binary search tree. Each time the data is inserted, the system first determines whether it is larger than the root node (current data > root node)? Insert from right: insert from left) this is a ternary operator. And the insertion is from the bottom of the leaf node to make a comparison and then choose whether it is on the left or right side of the leaf node. There will be a disadvantage: the height of the tree. The more data, the higher the height. As a result, it takes too long to query the lowest leaf node. So there is one of its red and black trees.
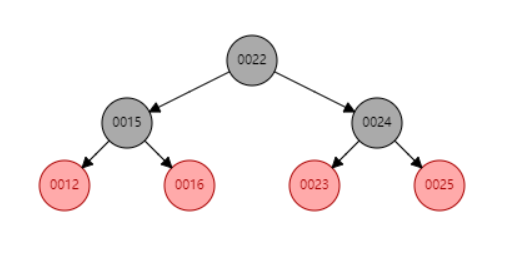
As shown in the picture: it is a red black tree. The red black tree maintains a different color between the two.
Each node is either red or black
Root node must be black
Red nodes cannot be continuous (children of red nodes cannot be red)
For each node, any path from that node to null (the end of the tree) contains the same number of black nodes.
Intuitively, the insertion of red black tree is similar to that of binary search tree, only maintaining two different colors and why is it a balanced binary tree? In order to solve this problem, some balancing operations are introduced: discoloration, rotation. Rotation is divided into left and right
Discoloration
Discoloration can be divided into many situations. This is just one of them, because it is not the focus of this time. If you are interested, you can find out.
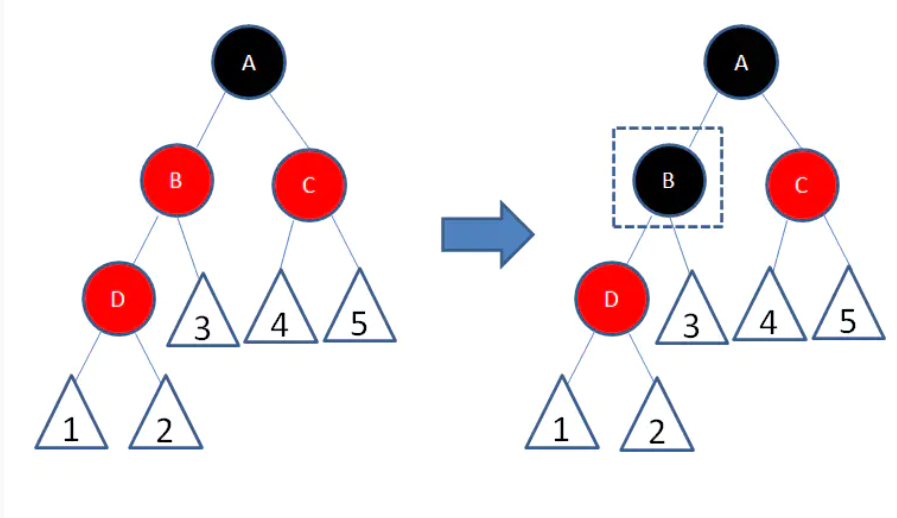
It can be seen from the figure that the left node child of B is also red. Obviously contrary to the concept of red black tree (red nodes can not be continuous), then after adjustment (on the right side of the way). Change node B to black. So we solved the problem of discontinuity. But there will be a new problem. There is one more black node in the side path, which causes the black nodes on both sides to be inconsistent.
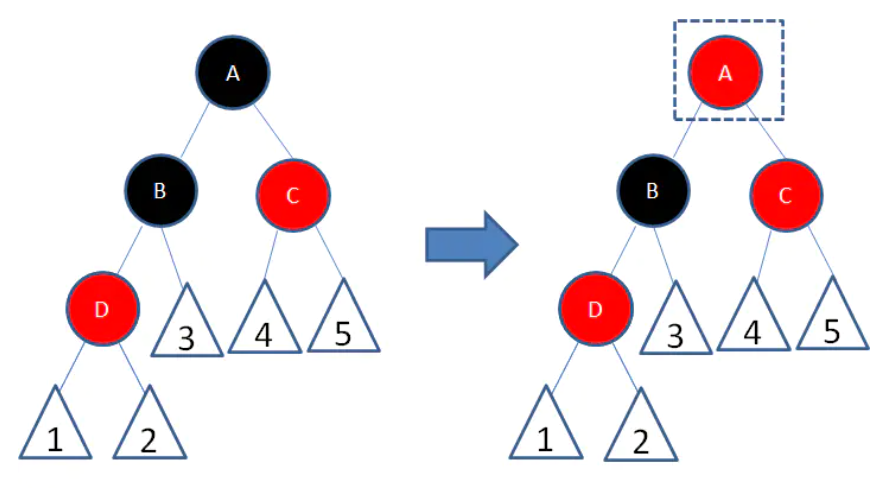
So we change the color of the parent node A of B to red. Although it solves the problem that the number of black nodes on both sides is the same, it will cause the last problem that can not be continuous. So we changed A's right node child to black. As shown in the figure below, both problems are solved.
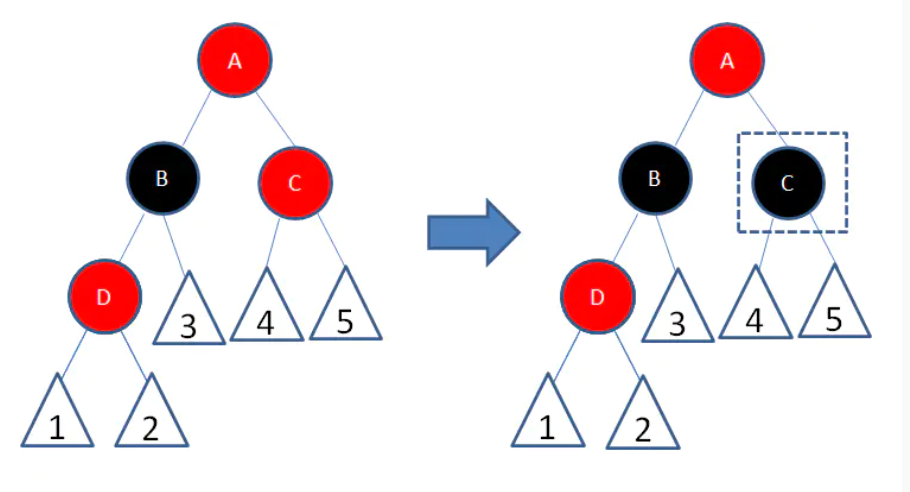
After learning how to adjust the balance by changing the color, let's see how the rotation works
rotate
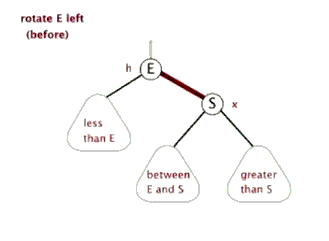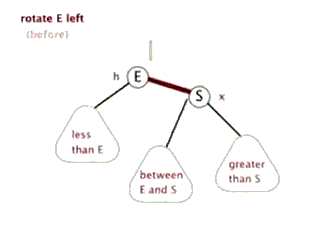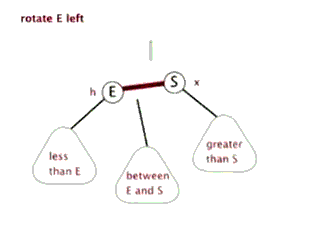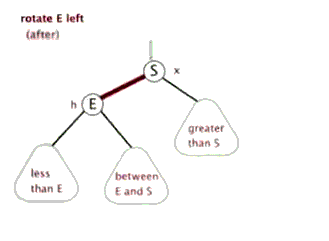
As we mentioned above, the rotation can be divided into left-hand rotation and right-hand rotation, so let's show them separately
Sinistral
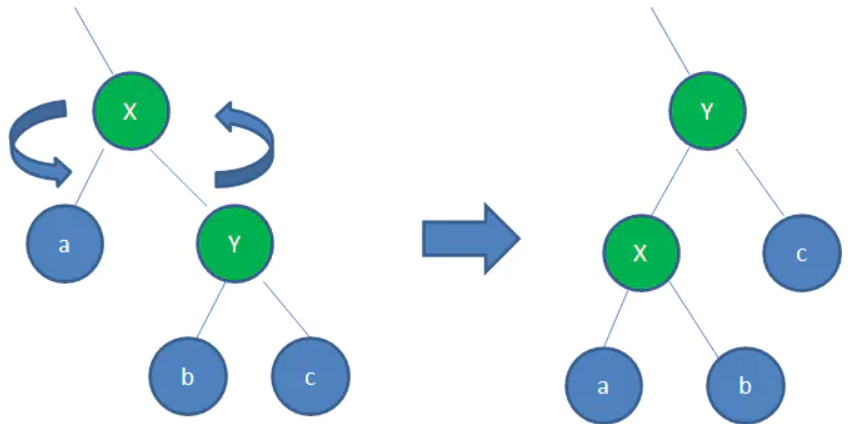
Left: your right node becomes your husband node. Instead, the left node of the right node becomes its own right node.
Dextral
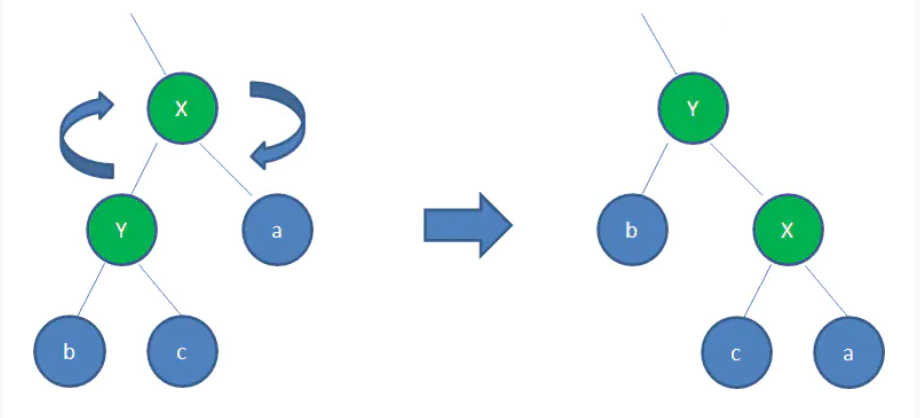
Right: your left node becomes your own parent. Instead, the right node of the left node becomes its own left node.
If you don't understand the rotation here, let's give you a group of dynamic display charts
At this point, it's over here. It's about the result of HashMap, but it's about the data structure. But there's no way. If you don't understand the above. You may not be able to read the following source code.
brief introduction
Said so much, finally arrived at the text. HashMap implements the Map interface. JDK1.7 is implemented by array + linked list, and 1.8 later by array + linked list + red black tree. It is a storage container in the form of key and value, and allows key to be null and value to be null. The container thread is not safe.
HashMap structure of JDK 1.7

HashMap structure of JDK 1.8
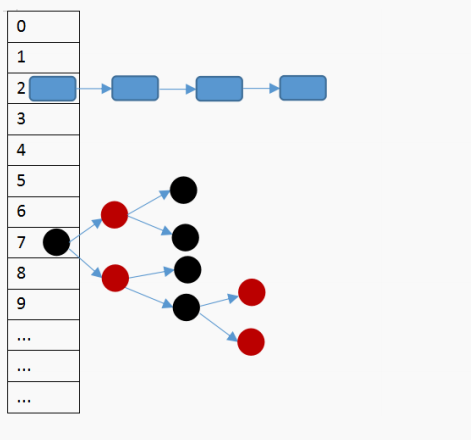
Basic elements of HashMap
/** * Default initial capacity 1 < 4 = = 2 ^ 4 = 16 */ static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16 /** * Maximum capacity 2 ^ 30 */ static final int MAXIMUM_CAPACITY = 1 << 30; /** * Default load factor * The load factor represents the usage of a current hash * The number of containers size > load factor * array length needs to be expanded */ static final float DEFAULT_LOAD_FACTOR = 0.75f; /** * JDK 1.8 newly added * If a linked list > = 8 in the array needs to be converted to a red black tree */ static final int TREEIFY_THRESHOLD = 8; /** * JDK 1.8 newly added * If a linked list in the array is converted to a red black tree node < 6, it will continue to be converted to a linked list */ static final int UNTREEIFY_THRESHOLD = 6; /** * JDk 1.8 newly added * If the linked list element is > = 8 and the array is > 64, the red black tree will be converted */ static final int MIN_TREEIFY_CAPACITY = 64; /** * From the previous entry, it should be changed to Node type, in fact, Node is Map.Entry Interface implementation class of. * (Entry Is an internal interface in the Map interface) */ transient Node<K,V>[] table; // Record the number of key value pairs transient int size; /** * Record the number of changes to elements in the collection */ transient int modCount; /** * Threshold: the number of elements that can be accommodated. When size > threshold, the capacity will be expanded * threshold = Load factor * array length */ int threshold;
Node
static class Node<K,V> implements Map.Entry<K,V> { // hash value final int hash; final K key; V value; // Lower node pointer Node<K,V> next; Node(int hash, K key, V value, Node<K,V> next) { this.hash = hash; this.key = key; this.value = value; this.next = next; }
Construction method
HashMap()
public HashMap() { // The default load factor is 0.75 this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted }
HashMap(int initialCapacity)
public HashMap(int initialCapacity) { this(initialCapacity, DEFAULT_LOAD_FACTOR); } // Specify initial capacity value, default load factor 0.75 public HashMap(int initialCapacity, float loadFactor) { // Initial capacity not less than 0 if (initialCapacity < 0) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); // If the initial capacity > 2 ^ 30, the capacity is 2 ^ 30 if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; // Load factor cannot be less than 0 | no value if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); // Load factor this.loadFactor = loadFactor; // threshold this.threshold = tableSizeFor(initialCapacity); }
HashMap(Map<? extends K, ? extends V> m)
// Create a new HashMap based on Map public HashMap(Map<? extends K, ? extends V> m) { this.loadFactor = DEFAULT_LOAD_FACTOR; putMapEntries(m, false); }
Add method put
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; // Create a new table when table is null if ((tab = table) == null || (n = tab.length) == 0) // Use resize() to create a new table n = (tab = resize()).length; //According to the data length and hash value, a numerical subscript is obtained by operation. If there is no element in the subscript, it will be stored directly if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); else { // Element already exists Node<K,V> e; K k; // There is a conflict, pointing to the first node if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; // If it's a red black tree. Store key value pairs. else if (p instanceof TreeNode) e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // If it is linked list storage else { // Circular list for (int binCount = 0; ; ++binCount) { // Until the end of the list, there is no duplicate key if ((e = p.next) == null) { // New node storage p.next = newNode(hash, key, value, null); // If chain len gt h > = specified value 8 - 1 if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st // Transformation of Mangrove treeifyBin(tab, hash); break; } // End the cycle if the same key is found if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } // If there is a duplicate key, the new value will replace the old one if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; // Whether expansion is needed if (++size > threshold) resize(); afterNodeInsertion(evict); return null; }
If you still don't understand the code level, use words to sort out the process
-
Call hash to get the hash value of the key
-
Determine whether the table is null. If NULL, create a new table array
-
Gets the subscript position based on the array length and hash value. If the subscript has no data, it will be stored directly
(1) If there is data, judge whether there is a conflict. The conflict directly obtains this node
(2) To determine whether to store in red black tree, the method in red black tree is used to store key value pairs.
(3) Linked list storage, circular linked list, whether there is data conflict with it
I. if there is no data conflict at the end of the cycle, insert it directly at the tail, and judge whether it is > = 8-1 to convert the red black tree
II. If there is a conflicting key, the loop will be terminated immediately and the node will be obtained at the same time
- Replace the old value with the new one
Note one point: if the user-defined type is the key of HashMap, the hashCode and equals methods need to be overridden at this time.
principle:
Override hashCode method: ensure that elements with the same content return the same hash value, and different elements return different hash values as much as possible.
Override equls method: objects with the same content return true.
After all, let's have some more pictures. Maybe the combination of the three can be more thorough. If you don't say much, just go to the picture above.
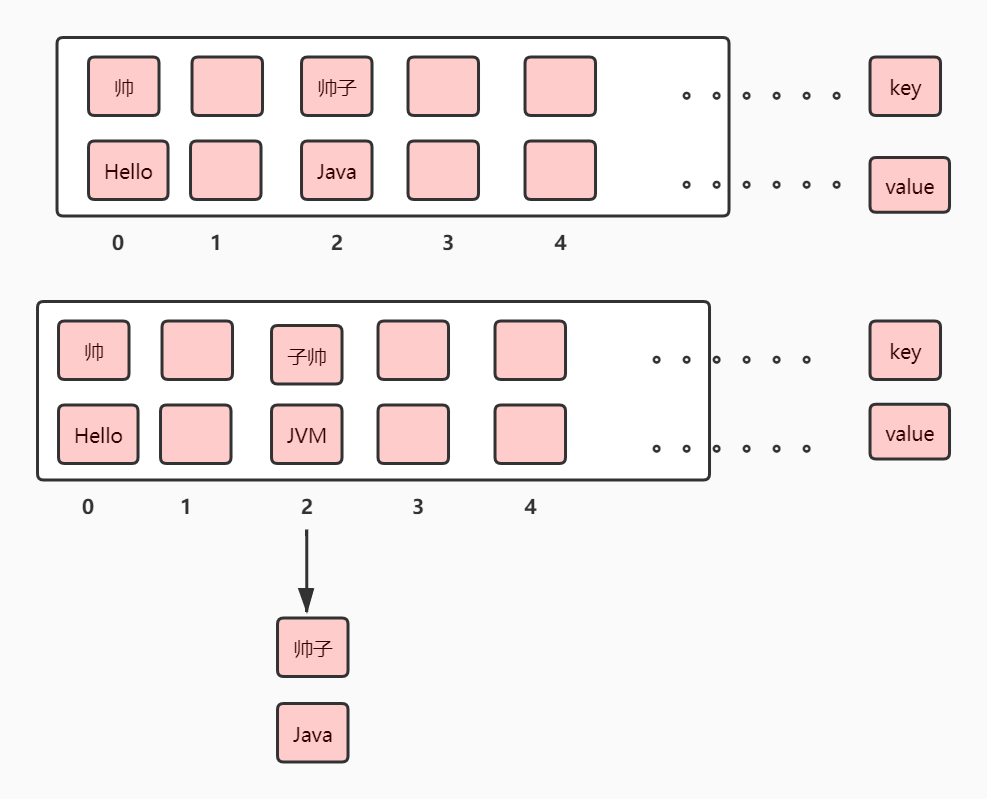
When inserting the data whose key is handsome, a subscript will be calculated through the hash and array length of the key. For example, at this time, the subscript is 0, and there is no data at this time. Then the data will be inserted here directly. When inserting a data for key shuaizi for the second time. Through the hash of key and the length of array, the subscript is 2. At this time, if there is no data here, insert it directly. As shown in Figure 1. We mentioned a linked list before. So where is the list. So look at Figure 2. At this time, we need to insert a key data for zishuai. In some way. Zishuai and shuaizi's hash may be the same. This will lead to data conflicts. At this time, the zipper method is used to solve the conflict problem. Here is a problem to pay special attention to: the figure above shows that the JDK 1.7 insertion method uses the head insertion method, that is, after the conflict between zishuai and shuaizi. Will put the child commander in the head node. Its back pointer points to shuaizi.
Why do you emphasize that JDK 1.7 uses plug-in? Isn't that kind of insertion after that
This is not the case for JDK 1.8. It's not kind of you to do it by yourself. 1.8 is not very different from the above figure, and it has been emphasized many times. Linked list > = 8-1 & & array length > 64 convert to red black tree. Let's make up the brain. Let's focus on tail insertion
Consider a question: why do we use tail plug? Is there any defect in head plug?
Let's think about this first. Detailed explanation will be provided during resize().
Get method get
final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; // tab is not null while table length > 0 and the corresponding subscript content under the array is not null if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { // If the key of the first node corresponding to the subscript of the array is the same as the key searched if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) // Return to the first node return first; // Different, there are other nodes if ((e = first.next) != null) { // Red black tree storage if (first instanceof TreeNode) // Get Node of key pair through red black tree return ((TreeNode<K,V>)first).getTreeNode(hash, key); // In the form of linked list, all nodes are traversed. do { // If the same direct return is found if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } // Return null if no return null; }
- If the table is not null and the corresponding storage subscript is not null for
- Determine whether the first node is the same. Return if same
- The first node is not the data you are looking for.
- If it is a red black tree storage, use the red black tree to obtain the corresponding Node
- Store the linked list, traverse the linked list, find the same key and return to Node
- If table is null, or there is no corresponding data, return null
Expand resize
JDK1.8 capacity expansion
final Node<K,V>[] resize() { Node<K,V>[] oldTab = table; int oldCap = (oldTab == null) ? 0 : oldTab.length; int oldThr = threshold; int newCap, newThr = 0; // table length > 0 if (oldCap > 0) { // Cannot expand if table length > = 2 ^ 30 if (oldCap >= MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE; // Return to the original array return oldTab; } // If the maximum space is not exceeded, it will be doubled else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) newThr = oldThr << 1; // double threshold } else if (oldThr > 0) // initial capacity was placed in threshold newCap = oldThr; else { // zero initial threshold signifies using defaults newCap = DEFAULT_INITIAL_CAPACITY; newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); } if (newThr == 0) { float ft = (float)newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE); } // Get new threshold threshold = newThr; // Create a new Node array and hash table based on the new capacity @SuppressWarnings({"rawtypes","unchecked"}) Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; if (oldTab != null) { // Traverse the original table to recalculate the position of each element for (int j = 0; j < oldCap; ++j) { Node<K,V> e; // The corresponding subscript element is not null if ((e = oldTab[j]) != null) { oldTab[j] = null; // There is only one element under the array if (e.next == null) // Store on new array newTab[e.hash & (newCap - 1)] = e; // Red black tree storage else if (e instanceof TreeNode) // Separate the red and black trees ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // preserve order // Linked list storage Node<K,V> loHead = null, loTail = null; Node<K,V> hiHead = null, hiTail = null; Node<K,V> next; // Get each node of the linked list do { next = e.next; if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } else { if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); if (loTail != null) { loTail.next = null; newTab[j] = loHead; } if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; } } } } } return newTab; }
JDK 1.7 capacity expansion
void resize(int newCapacity) { Entry[] oldTable = table; int oldCapacity = oldTable.length; if (oldCapacity == MAXIMUM_CAPACITY) { threshold = Integer.MAX_VALUE; return; } Entry[] newTable = new Entry[newCapacity]; transfer(newTable, initHashSeedAsNeeded(newCapacity)); table = newTable; threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1); } void transfer(Entry[] newTable, boolean rehash) { int newCapacity = newTable.length; // Array assignment after expansion for (Entry<K,V> e : table) { while(null != e) { Entry<K,V> next = e.next; // The value of the key will be recalculated here. Jdk 1.8 changed here if (rehash) { e.hash = null == e.key ? 0 : hash(e.key); } int i = indexFor(e.hash, newCapacity); e.next = newTable[i]; newTable[i] = e; e = next; } } }
It seems that there are so many source codes. Don't you think it's too boring? It seems that it's just like you don't understand. Very strange. It doesn't matter. Let's look at it with code and graphics. In this article, I will also explain why the tail interpolation method is adopted as mentioned before
Let's see the capacity expansion under single thread first
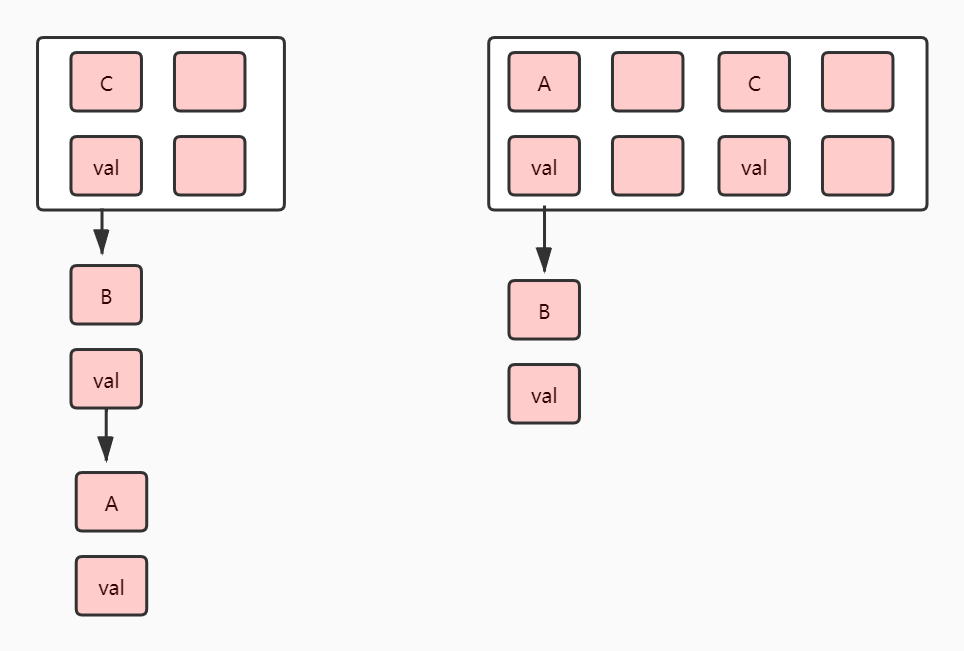
This is a single thread expansion. As the code says, the array will be expanded to twice the original size, and then all nodes will be traversed to assign values to the new array. Someone will say it at this time. Why are C running to other subscripts A and B still in the original subscript? Because the subscript depends on the hash and array length of the Key. If the array is expanded, the subscript will change in some cases. Is it true that every Key will be hashed once? In principle, this is the case, but it has been adjusted after 1.8. It will not lead to rehash, because each time a hash consumes a lot of performance.
Multithreading expansion
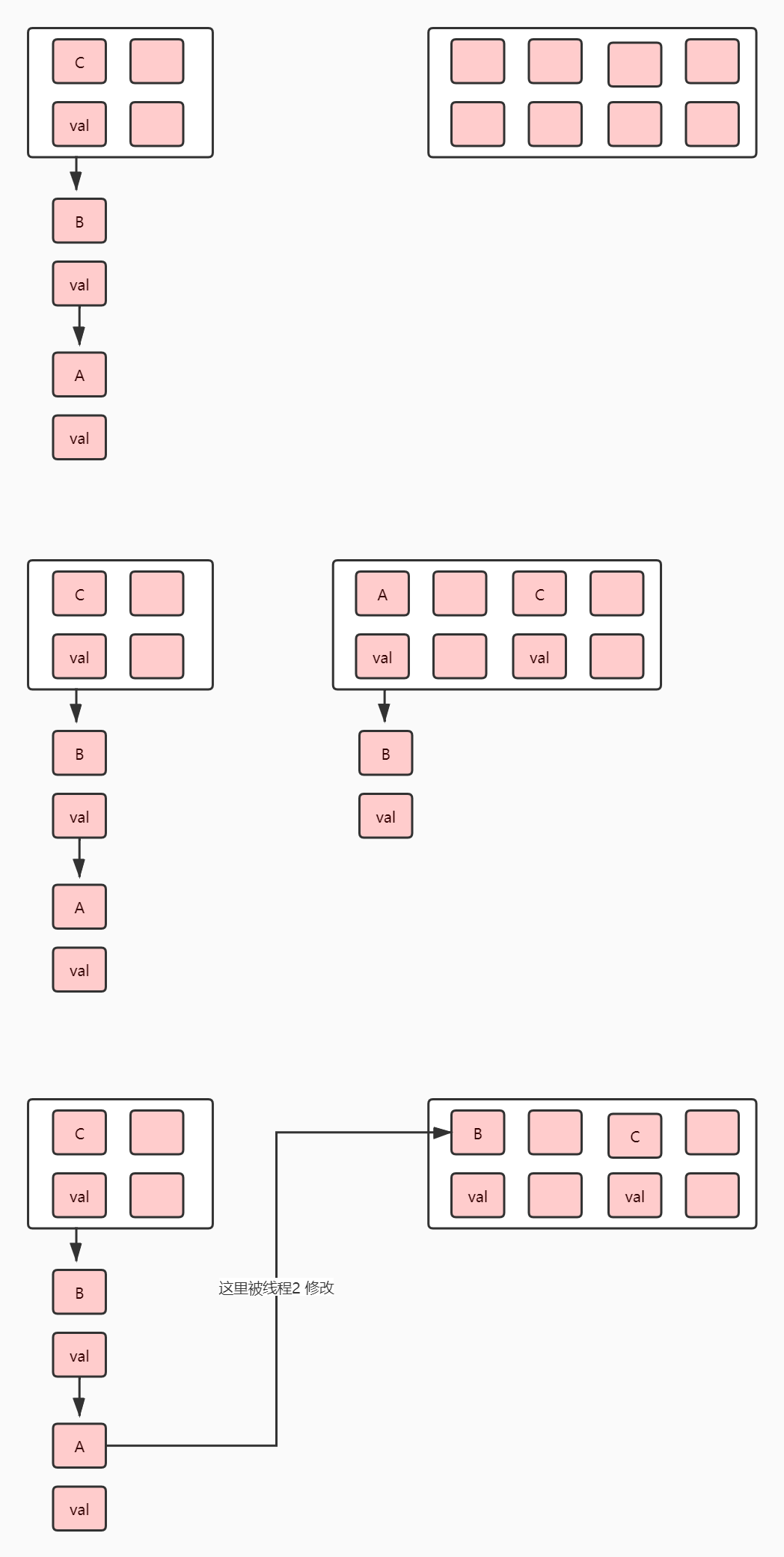
First, explain in advance the significance of the three above figures
- The first one is that thread 1 is suspended by CPU scheduling after the expansion is completed, starting at thread 2
- The second is that thread 2 starts to expand the capacity and then continues to execute thread 1 after the array assignment is finished
- The third is the continuation of thread 1
Let's explain one by one
First of all, I'd like to say something unpleasant in advance. When reading this passage, please take a look at the source code of the expansion and the single thread and multi-thread expansion diagram above. Have a macroscopic understanding and then taste this passage. To some extent, Xiaobian is not willing to repeat the same thing many times. Please understand!!!
Thread 1 is suspended after executing the capacity expansion method (in this case, it refers to the line of code that has completed the capacity expansion, not the whole capacity expansion method). It is not necessary to look at the above code to make up for it. Then thread 2 is executed. After expansion and recalculation of subscript. The state changes to the one shown on the right side of Figure 2. The original state is that B's next points to a, which is caused by the expansion of thread 2. At this time, a's next points to B. Thread 2 is suspended and starts to execute thread 1. At this moment, the next of thread 1's a does not point to null. After thread 2's processing, at this time, it points to B, which causes a particularly serious problem. A points to B, and B points to a, forming a dead cycle.
So we abandoned the head inserting method and introduced the tail inserting method. Why doesn't tail insertion cause these problems. I think the answer is already in your mind. If you haven't figured it out yet. Then you will follow the section "add put" in the article of Xiaobian to start step by step, insert the value with tail interpolation, and then try to expand the capacity. So here I will not introduce too much, want to know the little partner, has followed the small ideas in the drawing oh.
follow-up
That's all for today's article. See you next time.