Recognize the ordering of O(NlogN)

• Analysis of recursive behavior and estimation of time complexity of recursive behavior

  Using recursive method to find the maximum value in an array, what is the system doing?

  Supplementary knowledge: the binocular operator "> >" refers to shifting one bit to the right, which is calculated in binary. Shifting right is to add zero after the right and subtract the number of bits moved in front. After calculation, shifting one bit to the right is to divide by 2 and shifting one bit to the left is to multiply by 2. This operation is faster than division.

  //Find the maximum value in the range of array [l,..., R]
  public static int getMax(int[] arr){
      return process(arr,0,arr.length-1);
  }
  public static int process(int[] arr,int L,int R){
  	if(L==R){
          return arr[L];
      }
      int mid=L+((R-L) >> 1);//midpoint
      int leftMax=process(arr,L,mid);
      int rightMax=process(arr,mid+1,R);
      return Math.max(leftMax,rightMax);
  }
  //How is recursive behavior implemented on the system
  

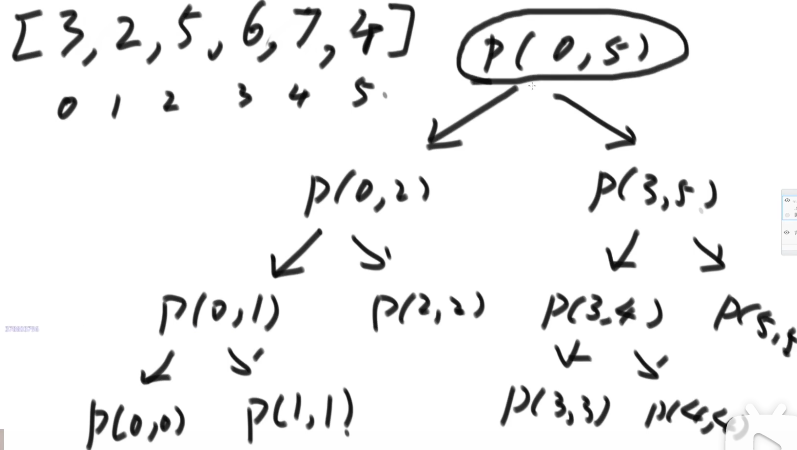
Press the stack in turn and return the left and right results. Use the stack to carry out a post order traversal.

• Use of master formula

  The method used to estimate a series of special recursive behaviors is an analysis method that is often used to use divide and conquer strategy to solve problems. (add: the recursive solution of divide and conquer strategy also has two common methods called substitution method and recursive tree method, which will have the opportunity to nag with relatives in the future). As we all know, In the divide and conquer strategy, recursion is used to solve the problem, which is divided into three steps: decomposition, solution and merger. The main method is expressed as follows:

  T [N] = aT[N/b] + O (Nd)

  The data volume of the parent problem is N, the scale of each sub process is N/b, and the number of calls is a. finally, the time complexity of the remaining processes except the called sub problems is determined.

• Analyze system recursive behavior

  T (N) is the total, the subproblem scale is N/2, the other subproblem data and other scales are called twice, and the final specific size behavior time complexity is O(1). The algorithm satisfying these conditions satisfies the master formula.

  T(N)=2T(N/2)+O(1)

  If the recursive sorting of master formula is satisfied, the time complexity is

  condition	Time complexity
  logba<d	O(Nd)
  logba>d	O(Nlogba)
  logba==d	O(Nd *logN)

  After generation calculation, the recursive behavior of the system, a=2,b=2,d=1, the time complexity is O(N), which is equivalent to traversing from left to right to find the maximum.

• Merge sort

  An unordered array is separated from the middle and sorted separately. The first bit of the array on the left is marked and the first bit of the array on the right is marked. Compare its size and define rules respectively. Assuming that the left tag bit is smaller than the right tag bit from small to large, create a temporary array, store the data on the left and move the left tag one bit to the right, If the mark on the right is small, the number of marks on the right will be put into the temporary array, and the mark on the right will move one bit to the right. In this process, if the mark on either side is offside, the rest of the array on the other side will be put into the temporary array, and then the value of the temporary array will be defined to the original array.

  public static void process(int[] arr,int L,Int R){
      if(L==R){
          return;
      }
      int mid=L+((R-L)>>1);
      process(arr,L,mid);
      process(arr,mid+1,R);
      merge(arr,L,mid,R);
  }
  public static void merge(int[] arr,int L,int M,int R){
      int[] temp=new int[R-L+1];
      int i=0;
      int p1=L;
      int p2=M+1;
      while(p1<=M && p2<=R){
          temp[i++]=arr[p1]<=arr[p2] ? arr[p1++]:arr[p2++];
      }
      while(p1<=M){
          temp[i++]=arr[p1++];
      }
      while(p2<=R){
          temp[i++]=arr[p2++];
      }
      for(i=0;i<temp.length;i++){
          arr[L+i]=temp[i];
      }
  }//Sort merge process
  

  T(N)=2T(N/2)+O(N) a=2 b=2 d=1

  O(N *logN)

  O(N2) is worse than O(N *logN) in that it makes redundant comparisons. For example, selecting sorting wastes a lot of comparisons, and only one is sorted at a time.

• Extension of merge sort

  Small sum problem: in an array, find the number smaller than him on the left of the position. How many are there? The small sum of the whole array is the sum of the small sums of each position. Violent solution O(N2)

  merge:

  public static int smallSum(int[] arr){
      if(arr===null || arr.length<2){
          return 0;
      }
      return process(arr,0,arr.length-1);
  }
  public static int process(intp[] arr,int l,int r){
      if(l==r){
          return 0;
      }
      int mid=l+((r-l)>>1);
      return process(arr,l,mid)
          +process(arr,mid+1,r)
      +merge(arr,l,mid,r);
  }
  public static int merge(int[] arr,int L,int m,int r){
      int[] temp=new int[r=L+1];
      int i=0;
      int p1=L;
      int p2=m+1;
      int res=0;
      while(p1<=m && p2<=r){
          res+=arr[p1]<arr[p2] ? (r-p2+1)*arr[p1]:0;
          temp[i++]=arr[p1]<arr[p2] ? arr[p1++]:arr[p2++];
      }
      while(p1<=m){
          temp[i++]=arr[p1++];
      }
      while(p2<=r){
          temp[i++]=arr[p2++];
      }
      for(i=0;i<temp.length;i++){
          arr[L+i]=temp[i];
      }
      return res;
  }
  

• Quick sort

  Question 1: given an array arr and a number num, please put the number less than or equal to num on the left of the array, the number greater than num on the right of the array, and the number equal to in the middle. Additional space complexity O(1) and time complexity O(N) are required. (Netherlands Flag issue)

  public static void quickSort(int[] arr,int L,int R){
      if(L<R){
          swap(arr,L+(int)(Math.random()*(R-L+1)),R);
          int[] p=partition(arr,L,R);
          quickSort(arr,L,p[0]-1);//< area
          quickSort(arr,p[1]+1,R);//>District
      }
  }
  public static int[] partition(int[] arr,int L,int R){
      int less=L-1; //< right boundary of area
      int more=R; //>Left boundary of area
      while(L<more){
          if(arr[L]<arr[R]){//L indicates the location of the current genus arr [R] - > division value
              swap(arr,++less,L++);
          }else if(arr[L]>arr[R]){//Current number < partition value
              swap(arr,--more,L);
          }else{
              L++;
          }
      }
      swap(arr,more,R);
      return new int[] {less+1,more};
  }
  public static void swap(int[] arr,int i,int j){
      arr[i]=arr[i]^arr[j];
      arr[j]=arr[i]^arr[j];
      arr[i]=arr[i]^arr[j];
  }