Experimental report of City College of Zhejiang University

1, Purpose of the experiment:

Understand the results of data type conversion and shift operation in high-level language, so as to better understand the requirements and problems to be considered in instruction system design and computer hardware design;

2, Experiment content:

1. Write a program to complete the type conversion in the experimental handout;
2. Write programs and test xor_swap function;
3. Write a program, test and modify reverse_array function;

3, Experimental steps

1. Write the program, complete the C language expression that meets the experimental content 1, and output the verification.

Source code:

#include <stdio.h>

typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, int len) {
    int i;
    printf("0x");
    for (i = 0; i < len; i++)
        printf(" %.2x", start[i]);
    printf("\n");
}
void show_int(int x) {
    show_bytes((byte_pointer) &x, sizeof(int));
}

int main(){
    int x = 0x12345678;
    //First question
    show_int(x & 0xff000000);
    //Second question
    show_int(x & 0xff);
    //Question 3
    show_int((x | 0xff) ^ 0xffffffff);
    //Question 4
    show_int(x | 0xff);
    return 0;
}

Operation results:

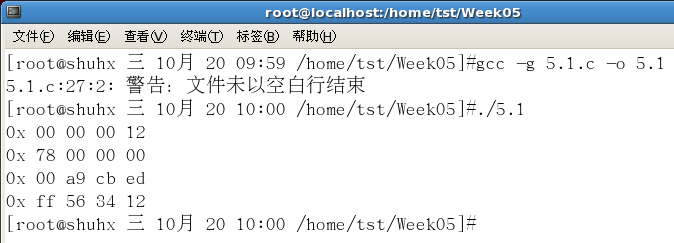
2. Write a program to realize the type conversion in experimental content 2, and explain the running results of the program.

Source code:

#include <stdio.h>

typedef unsigned char *byte_pointer;

void show_bytes(byte_pointer start, int len) {
    int i;
    printf("0x");
    for (i = 0; i < len; i++)
        printf(" %.2x", start[i]);
    printf("\n");
}
void show_int(int x) {
    printf("%d\t", x);
    show_bytes((byte_pointer) &x, sizeof(int));
}
void show_short(short x) {
    printf("%d\t", x);
    show_bytes((byte_pointer) &x, sizeof(short));
}
void show_float(float x) {
    printf("%f\t", x);
    show_bytes((byte_pointer) &x, sizeof(float));
}
void show_double(double x) {
    printf("%f\t", x);
    show_bytes((byte_pointer) &x, sizeof(double));
}
void show_unsigned_short(unsigned short x) {
    printf("%u\t", x);
    show_bytes((byte_pointer) &x, sizeof(unsigned short));
}
void show_unsigned_int(unsigned int x) {
    printf("%u\t", x);
    show_bytes((byte_pointer) &x, sizeof(unsigned int));
}

int main(){
    //First question
    short s = -12345;
    printf("Numb1\nint: ");
    show_int((int) s);
    printf("unsigned short: ");
    show_unsigned_short((unsigned short) s);
    printf("unsigned int: ");
    show_unsigned_int((unsigned int) s);
    printf("float: ");
    show_float((float) s);
    //Second question
    int x = 2147483647;
    printf("\nNumb2\nshort: ");
    show_short((short) x);
    printf("unsigned short: ");
    show_unsigned_short((unsigned short) x);
    printf("unsigned int: ");
    show_unsigned_int((unsigned int) x);
    printf("float: ");
    show_float((float) x);
    //Question 3
    float f = 123456.789e5;
    printf("\nNumb3\ndouble: ");
    show_double((double) f);
    //Question 4
    double d = 123456789e5;
    printf("\nNumb4\nfloat: ");
    show_float((float) f);
    //Question 5
    short sm = -12345;
    unsigned short  usm = -12345;
    printf("\nNumb5\nshort LM: ");
    show_short(sm << 2);
    printf("short RM: ");
    show_short(sm >> 2);
    printf("unsigned short LM: ");
    show_unsigned_short(usm << 2);
    printf("unsigned short RM: ");
    show_unsigned_short(usm >> 2);
    return 0;
}

Operation results:

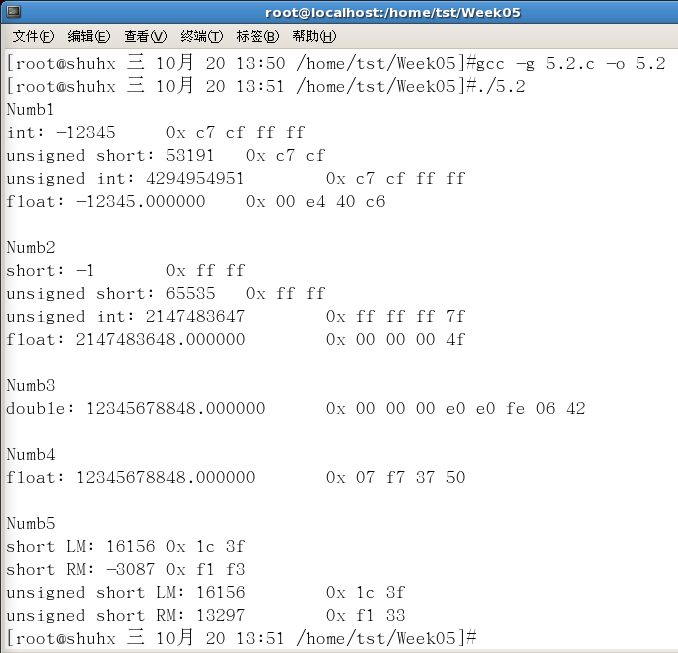
Interpretation of operation results:

First question

• s (0xCFC7) from short to int has no precision loss, and the data in memory is still saved in the original complement order. It is worth noting that here, due to the use of small end storage, the last output hexadecimal code and complement are inverse to each other
• Short to unsigned short sign bits are converted to numeric bits, and there is a change in data. In detail, after 0xCFC7 is converted to an unsigned value, the specific value does not change, but the interpretation of the value has changed. The original symbolic bits are converted to numerical bits (original 15 bits – > 16 bits), so it is 53191 after conversion to decimal
• short is converted to int first and then to unsigned int, so the internal code of unsigned in t is consistent with that of int. Specifically, in the second part of the conversion process, the symbol bit is also converted to numerical bit (originally 31 bits – > 32 bits), so it is 4294954951 after conversion to decimal
• Converting short to float may cause loss of accuracy. Specifically, the symbol bit is 1, the order code is 127 + 13 = 140, and the mantissa is 0x40E400, that is, 0xC640E400 (there is no precision loss here)

Second question

• X (0x7FFFFFFF) will be truncated from int to short, that is, only the lower 4 bits (0xFFFF) will be reserved, so the decimal system is - 1
• int is first converted to short and then to unsigned short. Specifically, in the second part, the sign bit is converted to value, so the decimal system is 65535
• Int to unsigned int, that is, the sign bit is converted to value, so the decimal system is 2147483647
• Int to float may cause loss of accuracy. Specifically, the symbol bit is 0, the order code is 127 + 30 = 157, and the mantissa is 0x3ffffff, that is, 0x4EFFFFFF. However, because the int here is special, rounding occurs. When representing the mantissa, it is considered to be 1.0 under C99 (actual 0.11... 1), so the order code is 127 + 31 = 158, the mantissa is approximately 0, and the final output hexadecimal is 0x4F000000

Question 3

• The conversion of F from float to double is not a problem, but the occupied length is changed from 4 bits to 8 bits. But the assignment statement float f = 123456.789e5; The essence is to convert int to float and then assign value. During this process, rounding occurs, and the final value of F is 12345678848.0 (0x5037F707). Therefore, it is 12345678848.0 after being converted to double, and the hexadecimal representation is 0x4206FEE0E00000000

Question 4

• d changing from double to float may cause loss of accuracy. Similarly, here, int is converted to double without rounding. The final value of d is 12345678900.0, and the hexadecimal representation is 0x4206FEE0E1A00000. Rounding occurs in the second part of the process, so it is 12345678848.0 and 0x5037F707 after being converted to float.

Question 5

• sm (0xCFC7) is 0x3F1C after shifting two bits to the left, and 0xF3F1 after shifting two bits to the right (because it is a signed number, the arithmetic shift to the right is adopted, and the highest bit is supplemented by the sign bit). usm (53191, 0xCFC7) is 0x3F1C after shifting two bits to the left, and 0x33F1 after shifting two bits to the right (because it is a signed number, arithmetic shift to the right is adopted, and the highest bit is supplemented by the sign bit).

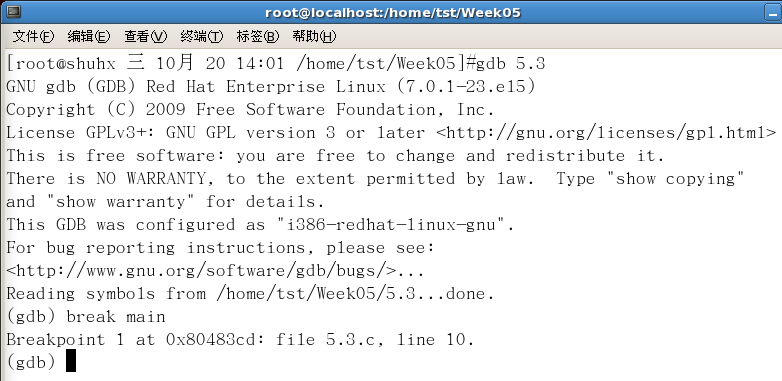
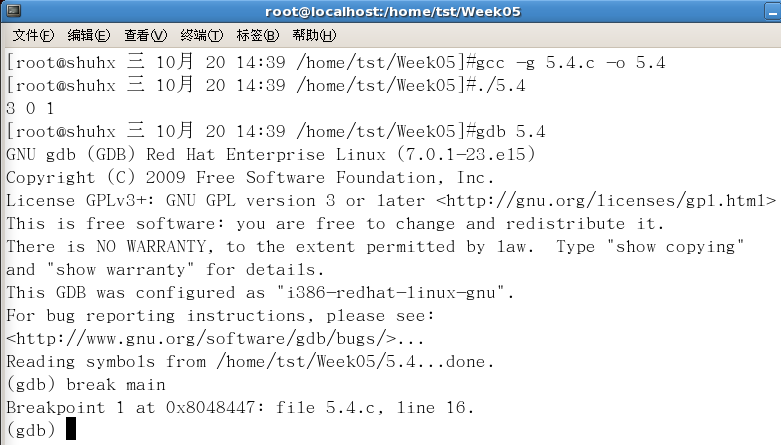
3. Write the test program test1.c and call XOR in experiment content 3_ Swap function, and use gdb tool to debug the program to view the execution results of each step.

Source code:

#include <stdio.h>

void xor_swap(int *x, int *y) {
    *y = *x ^ *y;
    *x = *x ^ *y;
    *y = *x ^ *y;
}

int main(){
    int x = 1, y = -1;
    xor_swap(&x, &y);
    printf("x:%d\tY:%d\n", x, y);
    return 0;
}

Screenshot of commissioning process:

Commissioning preparation

Set breakpoint

View the execution results of each step

• Initialize x, y

• *y = *x ^ *y;

• *x = *x ^ *y;

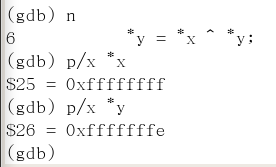
• *y = *x ^ *y;

• After the function ends

Explanation of operation results of each step:

step	*x	*y
initial	a	b
*y = *x ^ *y	a	a ^ b
*x = *x ^ *y	a ^ (a ^ b) = (a ^ a) ^ b = b	a ^ b
*y = *x ^ *y	b	b ^ (a ^ b) = (b ^ b) ^ a = a

4. Write the test program test2.c and call reverse in experiment content 4_ Array and XOR in Experiment 2_ Swap function, and use gdb tool to debug the program, view the execution results of each step, answer the questions in experiment content 4, and modify the program to make it correct.

Source code:

#include <stdio.h>

void xor_swap(int *x, int *y) {
    *y = *x ^ *y;
    *x = *x ^ *y;
    *y = *x ^ *y;
}
void reverse_array(int a[], int len) {
    int left, right = len - 1;
    for (left = 0; left <= right; left++, right--) {
        xor_swap(&a[left], &a[right]);
    }
}

int main(){
    int c[3] = {1, 2, 3};
    reverse_array(c, 3);
    for (i = 0; i < 3; i++){
        printf("%d ", c[i]);
    }
    printf("\n");
    return 0;
}

Screenshot of commissioning process:
Commissioning preparation

Set breakpoint

View the execution results of each step

• Initialize array

• Enter the function call with the problem in the for loop

• Initialize * x, * y

• *y = *x ^ *y

• *x = *x ^ *y

• *y = *x ^ *y

• After the function ends

Explanation of operation results of each step:

• reverse_ The effect of the array function is to call XOR on the specified part of a specified array from both ends_ Swap function to flip the array. But in reverse_ In the for loop in the array function, because the passed in len may be an odd number, left and right will point to the same position, and the operation result is 0, as shown in the following figure

step	*x	*y
initial	a	a
*y = *x ^ *y	a	a ^ a = 0
*x = *x ^ *y	0 ^ 0 = 0	0
*y = *x ^ *y	0	0

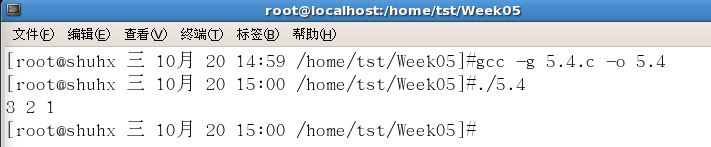
Modified reverse_array code:

void reverse_array(int a[], int len) {
    int left, right = len - 1;
    for (left = 0; left < right; left++, right--) {
        xor_swap(&a[left], &a[right]);
    }
}

Modified program running results:

4, Thinking questions

1. Are unsigned numbers and signed integers extended in the same way? How are they carried out?

Different

• For unsigned numbers, expand the number of digits, that is, fill 0 in the high position; For signed numbers, expand the number of bits, that is, fill the sign bit in the high position.

2. Can complement integers (such as int type numbers) always be converted to equivalent float type data? Why?

not always

• For example, the valid value of int can be up to 31 bits, while the precision of float is up to 23 bits. If the compiler recognizes the loss of precision during conversion, rounding operation will occur to the, accompanied by the loss of precision.

3. Can float data always be converted into equivalent double data? Why?

sure

• The composition of float under IEEE754 is 1-bit symbol bit, 8-bit order code and 23 bit mantissa; double is composed of 1-bit sign bit, 11 bit order code and 52 bit mantissa. Obviously, there will be no problem with the conversion.

4. What happens when long numbers are truncated into short numbers? Why?

If the number of significant digits is still less than the truncation number, the size does not change.

• If the number of significant digits is still greater than the truncated number and the short number is unsigned, the value will become smaller; If it is a signed number, it will change with the sign bit, so there are three cases here
  1. Normal (this is only for data attributes that have not changed, not for specific values)
  2. Positive overflow (positive to negative)
  3. Negative overflow (negative to positive)

5. Is the shift operation rule in C language related to the data type of the operation object?

Shift right is related to shift left is irrelevant

• The left shift is to make up 0 in the low position
• Shift right for unsigned numbers, fill 0 in the high order; For signed numbers, sign bits are filled in the high order

6. How many times are the operations of shifting 2 bits left and 2 bits right equivalent to expanding and shrinking respectively?

Quadruple, quadruple