The principle of YOLOv5 will not be described too much here. Start directly from the output head, and then design such as encoding and decoding:
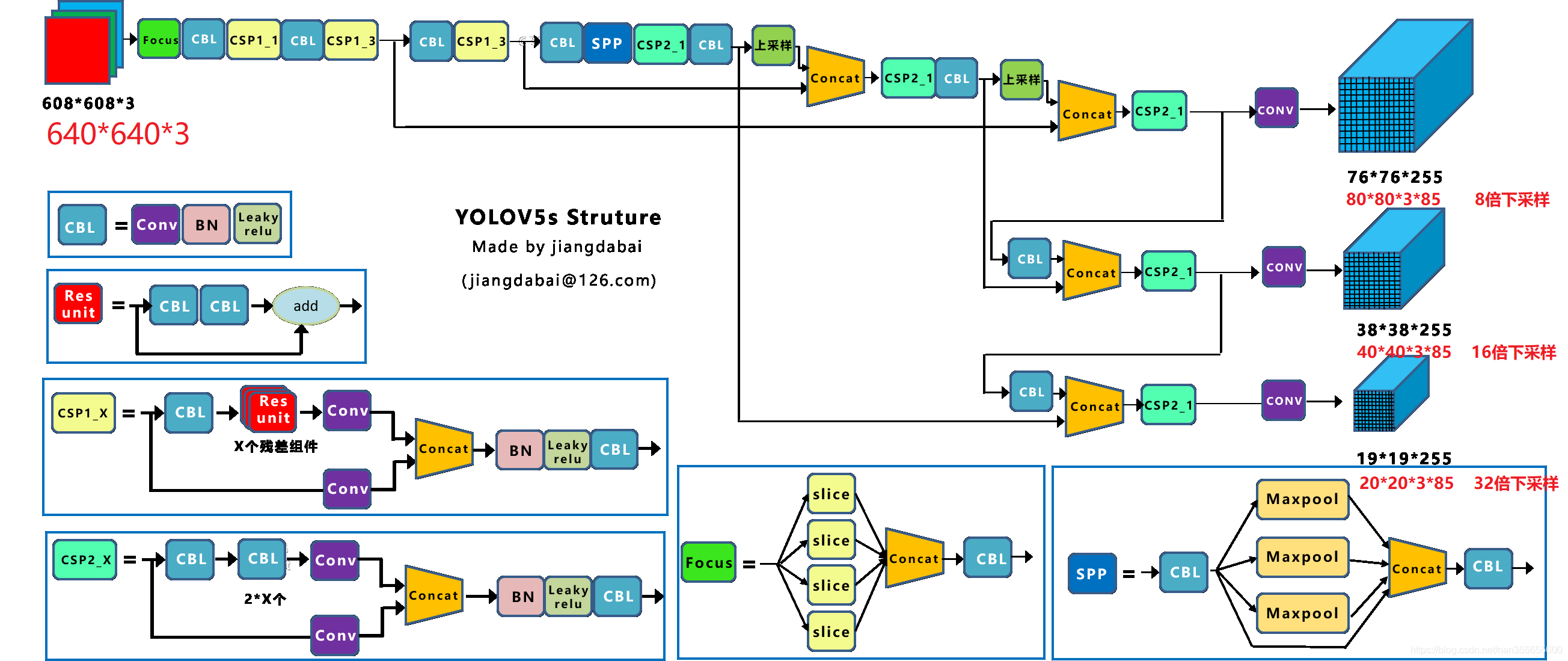
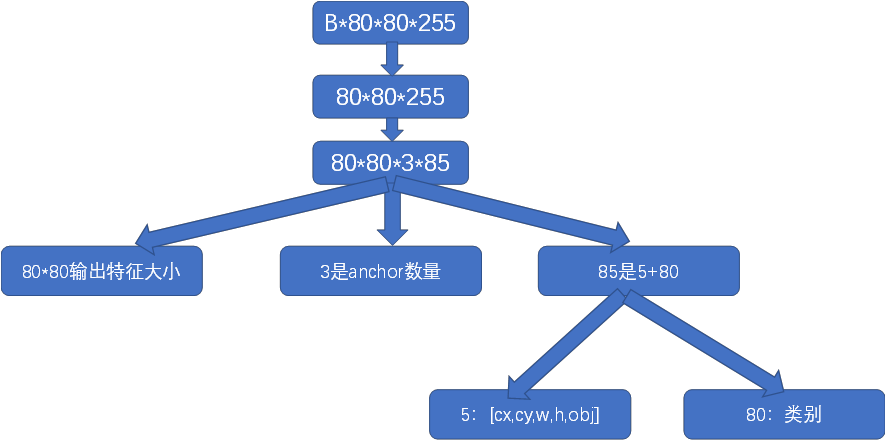
1. The original output of yolov5 series is three head heads. The picture above is the picture with the input resolution of 608 * 608. If the input is changed to the picture with the resolution of 640 * 640, the three output heads correspond to three 8, 16 and 32 respectively, and the output of down sampling is 80 * 80 * 255, 40 * 40 * 255 and 20 * 20 * 255 respectively. The corresponding digital meaning is shown in the above figure.
2. So What do the numbers 80 * 80 * 255, 40 * 40 * 255 and 20 * 20 * 255 mean respectively, where B is batch
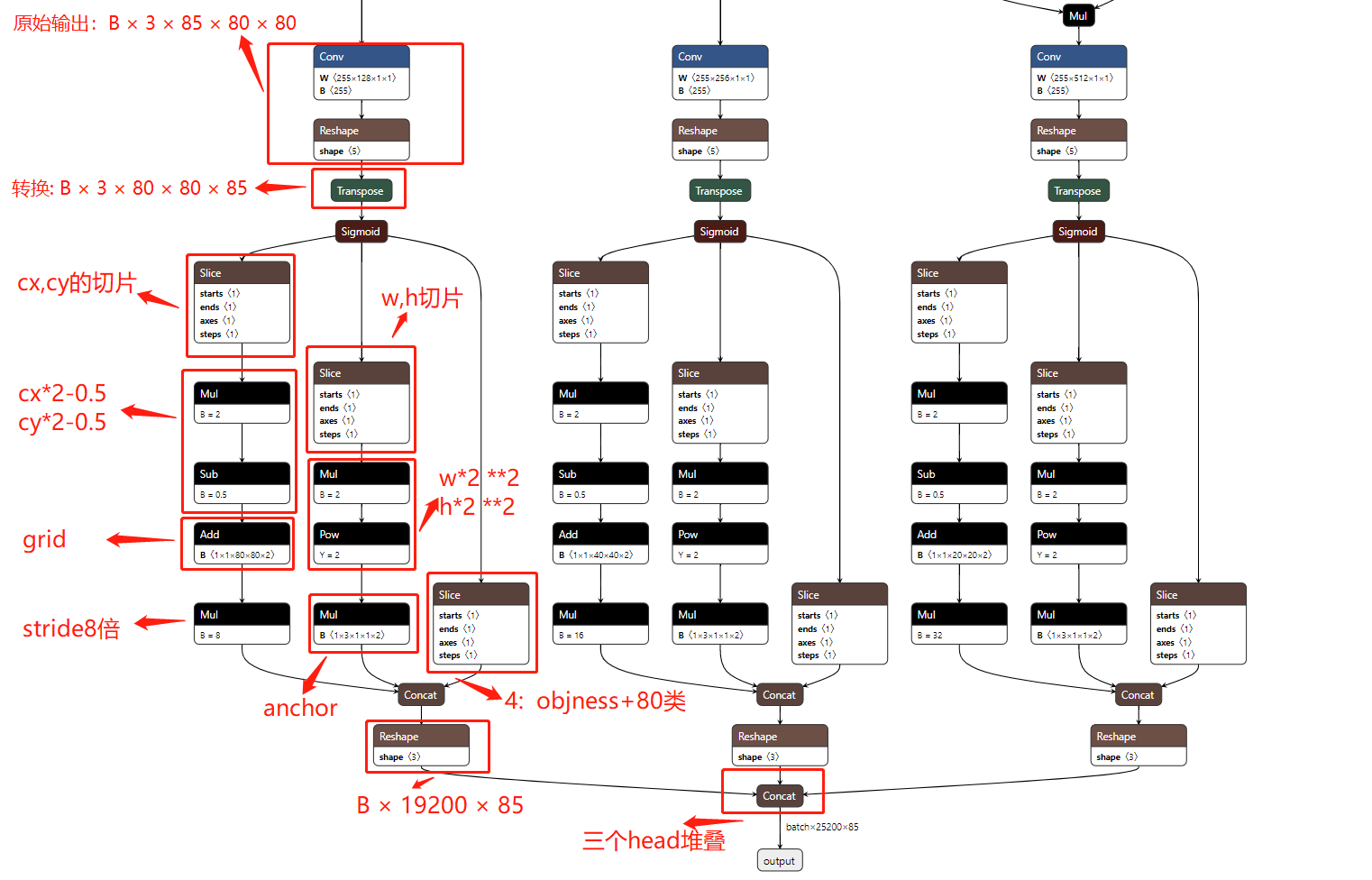
3 the three heads output in the figure above are not the final output, and a lot of work needs to be done. If they are output directly in this way, subsequent code decoding is very troublesome. Therefore, these three heads need to be further processed to facilitate the decoding operation of subsequent codes. Specifically, the following work is done:
three point one sigmoid activation function is required
3.2 xy*2-0.5
3.3 (wh*2)**2*anchor
3.4 get the frame under 640 scale
It can be seen that many operations are required, which are very troublesome and can be done by onnx. Therefore, in order to better access in continuous space, the following output channels can be transformed, that is, the original B*3*85*80*80 can be transformed into B*3*80*80*85. Such tensor can be easily operated, but it is still troublesome because there are three heads, Then you can continue to merge, that is, B*19200*85. The other three headers are similar:

At this time, you need to modify the python code exported by yolo to support the export of onnx:
The code for modifying python is in E: \ project \ C + + \ yolov5 master \ models \ yolo.py
def forward(self, x):
z = [] # inference output
for i in range(self.nl):
x[i] = self.m[i](x[i]) # conv
# bs, _, ny, nx = x[i].shape # x(bs,255,20,20) to x(bs,3,20,20,85)
bs, _, ny, nx = map(int, x[i].shape) # x(bs,255,20,20) to x(bs,3,20,20,85)
# x[i] = x[i].view(bs, self.na, self.no, ny, nx).permute(0, 1, 3, 4, 2).contiguous()
x[i] = x[i].view(-1, self.na, self.no, ny, nx).permute(0, 1, 3, 4, 2).contiguous()
if not self.training: # inference
if self.grid[i].shape[2:4] != x[i].shape[2:4] or self.onnx_dynamic:
self.grid[i] = self._make_grid(nx, ny).to(x[i].device)
y = x[i].sigmoid()
# if self.inplace:
if self.inplace:
y[..., 0:2] = (y[..., 0:2] * 2. - 0.5 + self.grid[i]) * self.stride[i] # xy
y[..., 2:4] = (y[..., 2:4] * 2) ** 2 * self.anchor_grid[i] # wh
else: # for YOLOv5 on AWS Inferentia https://github.com/ultralytics/yolov5/pull/2953
xy = (y[..., 0:2] * 2. - 0.5 + self.grid[i]) * self.stride[i] # xy
wh = (y[..., 2:4] * 2) ** 2 * self.anchor_grid[i].view(1, self.na, 1, 1, 2) # wh
y = torch.cat((xy, wh, y[..., 4:]), -1)
z.append(y.view(bs, -1, self.no))
return x if self.training else (torch.cat(z, 1), x)The onnx after export should be as follows:
The above is the work before onnx. After decoding, tensorrt should be used for reasoning. The whole code is In my github,
Here are the key codes:
1. Preprocessing kernel function
/* Data preprocessing */
static __global__ void warp_affine_bilinear_and_normalize_plane_kernel(uint8_t* src, int src_line_size, int src_width, int src_height, float* dst, int dst_width, int dst_height,
uint8_t const_value_st, float* warp_affine_matrix_2_3, Norm norm, int edge){
/* The implementation principle of warpaffine here is the same as that of python. The difference is that the implementation here is implemented through cuda multithreading. The specific implementation principle is as follows
* What needs to be determined here is that in order to minimize the amount of calculation, the pixels of the target image are traversed. Obviously, the pixel size of the target image is determined, no matter how large the input image size is
Finally, I will change to the target image size. For example, the image input to the deep learning model should be 640x640, and the size of the original image is 1080x1920. Obviously, the calculation of traversing the original image is very large
The traversal target image is fixed and small, so how to do this affine transformation?
1. Firstly, the input affine transformation matrix is from the point of the original image -- > the point of the target image, so it is necessary to take the inverse transformation to obtain the point of the target image -- > the point of the original image
2. When transforming to the point position of the original picture, the pixel value of the point at the original position will be calculated by bilinear transformation
3. How to calculate? Here we need to understand that the essence of double lines is to calculate the value of a point through the values of four points, so the point transformed to the original picture is the point value we need to calculate,
The calculated value will be directly assigned to the corresponding position of the target image, but how to select these four points? In fact, it is very simple. Just take four adjacent points, such as:
(0,0) (1,0) (250,250) (251,250)
(0,1) (1,1) (250,251) (251,251)
The selection of these four points is the adjacent four points of the transformed points. How to do it? Round up and down, as shown in the above two points,
If the point from the target to the original picture is (250.35250.65), then this point is just within the range of the above four points, and the calculated relative position is (0.35,0.65)
Then, the value of the point is calculated through bilinear, and the value of the point is directly assigned to the position of the target point to be solved. After understanding this step, we basically understand it completely
*/
/* The understanding here is similar to the understanding of python version. The main consideration is CUDA Programming and multi-threaded code of CUDA
The incoming edge is the boundary of the thread, that is, the thread required by all tasks
*/
int position = blockDim.x * blockIdx.x + threadIdx.x;
if (position >= edge) return;
/* Get the relevant parameters of the matrix */
float m_x1 = warp_affine_matrix_2_3[0];
float m_y1 = warp_affine_matrix_2_3[1];
float m_z1 = warp_affine_matrix_2_3[2];
float m_x2 = warp_affine_matrix_2_3[3];
float m_y2 = warp_affine_matrix_2_3[4];
float m_z2 = warp_affine_matrix_2_3[5];
/* Because the data storage is one-dimensional linear storage, it is necessary to obtain the width and height limit of the target image through calculation */
int dx = position % dst_width;
int dy = position / dst_width;
/* The position of the point in the original picture is calculated through the point of the target. It is necessary to align the geometric center of the source image and the target image.
float src_x = m_x1 * dx + m_y1 * dy + m_z1 + 0.5f;
float src_y = m_x2 * dx + m_y2 * dy + m_z2 + 0.5f;
*/
float src_x = m_x1 * dx + m_y1 * dy + m_z1;
float src_y = m_x2 * dx + m_y2 * dy + m_z2;
float c0, c1, c2;
/* Check the edge condition. If it is an edge, assign a constant value directly */
if(src_x <= -1 || src_x >= src_width || src_y <= -1 || src_y >= src_height){
// out of range
c0 = const_value_st;
c1 = const_value_st;
c2 = const_value_st;
}else{
/* floorf(x) Gets the maximum integer not greater than x. In fact, these two points are the four adjacent points taking the original coordinates */
int y_low = floorf(src_y);
int x_low = floorf(src_x);
int y_high = y_low + 1;
int x_high = x_low + 1;
/* The following is the code for calculating interpolation */
uint8_t const_value[] = {const_value_st, const_value_st, const_value_st};
float ly = src_y - y_low;
float lx = src_x - x_low;
float hy = 1 - ly;
float hx = 1 - lx;
float w1 = hy * hx, w2 = hy * lx, w3 = ly * hx, w4 = ly * lx;
uint8_t* v1 = const_value;
uint8_t* v2 = const_value;
uint8_t* v3 = const_value;
uint8_t* v4 = const_value;
if(y_low >= 0){
if (x_low >= 0)
v1 = src + y_low * src_line_size + x_low * 3;
if (x_high < src_width)
v2 = src + y_low * src_line_size + x_high * 3;
}
if(y_high < src_height){
if (x_low >= 0)
v3 = src + y_high * src_line_size + x_low * 3;
if (x_high < src_width)
v4 = src + y_high * src_line_size + x_high * 3;
}
/*
c0 = w1 * v1[0] + w2 * v2[0] + w3 * v3[0] + w4 * v4[0];
c1 = w1 * v1[1] + w2 * v2[1] + w3 * v3[1] + w4 * v4[1];
c2 = w1 * v1[2] + w2 * v2[2] + w3 * v3[2] + w4 * v4[2];
*/
c0 = floorf(w1 * v1[0] + w2 * v2[0] + w3 * v3[0] + w4 * v4[0] + 0.5f);
c1 = floorf(w1 * v1[1] + w2 * v2[1] + w3 * v3[1] + w4 * v4[1] + 0.5f);
c2 = floorf(w1 * v1[2] + w2 * v2[2] + w3 * v3[2] + w4 * v4[2] + 0.5f);
}
if(norm.channel_type == ChannelType::SwapRB){
float t = c2;
c2 = c0; c0 = t;
}
if(norm.type == NormType::MeanStd){
c0 = (c0 * norm.alpha - norm.mean[0]) / norm.std[0];
c1 = (c1 * norm.alpha - norm.mean[1]) / norm.std[1];
c2 = (c2 * norm.alpha - norm.mean[2]) / norm.std[2];
}else if(norm.type == NormType::AlphaBeta){
c0 = c0 * norm.alpha + norm.beta;
c1 = c1 * norm.alpha + norm.beta;
c2 = c2 * norm.alpha + norm.beta;
}
/*
What needs to be explained here is that because the incoming pointer is a float type pointer, and because the data storage is one-dimensional, the author stores the three channels separately, so each channel
The occupied area size is area = dst_width * dst_height, then fill in the values respectively
*/
int area = dst_width * dst_height;
float* pdst_c0 = dst + dy * dst_width + dx;
float* pdst_c1 = pdst_c0 + area;
float* pdst_c2 = pdst_c1 + area;
*pdst_c0 = c0;
*pdst_c1 = c1;
*pdst_c2 = c2;
}
static void warp_affine_bilinear_and_normalize_plane(
uint8_t* src, int src_line_size, int src_width, int src_height, float* dst, int dst_width, int dst_height,
float* matrix_2_3, uint8_t const_value, const Norm& norm,
cudaStream_t stream) {
/* The jobs passed in here are actually the product of the width and height of the target image. The purpose is that gpu acceleration needs to be turned on later, and multithreading needs to be turned on. The number of multithreads is the product of the width and height of the target image */
int jobs = dst_width * dst_height;
auto grid = grid_dims(jobs);
auto block = block_dims(jobs);
checkCudaKernel(warp_affine_bilinear_and_normalize_plane_kernel << <grid, block, 0, stream >> > (
src, src_line_size,
src_width, src_height, dst,
dst_width, dst_height, const_value, matrix_2_3, norm, jobs
));
}2. Decoding kernel function
const int NUM_BOX_ELEMENT = 7; // left, top, right, bottom, confidence, class, keepflag
static __device__ void affine_project(float* matrix, float x, float y, float* ox, float* oy){
*ox = matrix[0] * x + matrix[1] * y + matrix[2];
*oy = matrix[3] * x + matrix[4] * y + matrix[5];
}
/* Decoding kernel function */
static __global__ void decode_kernel(float* predict, int num_bboxes, int num_classes, float confidence_threshold, float* invert_affine_matrix, float* parray, int max_objects){
/* The main parameter needed here is the passed in parameter num_bboxes is 25200, which is the output concat of three head s, as follows:
* B × 3 × 85 × 80 × 80 --> B × 3 × 80 × 80 × 85 --> B × 19200 × 85
B × 3 × 85 × 40 × 40 --> B × 3 × 40 × 40 × 85 --> B × 4800 × 85 ----> B × 25200 × 85
B × 3 × 85 × 20 × 20 --> B × 3 × 20 × 20 × 85 --> B × 1200 × 85
It can be seen that it is the output exported by onnx. 25200 is the concat of three head s, and each is the point of the characteristic graph. This must be understood,
Corresponding to each two-dimensional position of the feature map, the storage method is one-dimensional. Therefore, to obtain the data, you need to obtain the data through calculation. Here, B is 1 at this time
*/
/* 25600 threads are enabled for acceleration, but only 25200 threads are actually required for acceleration */
int position = blockDim.x * blockIdx.x + threadIdx.x;
if (position >= num_bboxes) return;
/*
It should be easy to understand here, because the data is 1 × twenty-five thousand and two hundred × 85. The data is stored sequentially during data storage, in which the first 25200 data are open parallel threads, that is, 25200 starts processing at the same time,
This is followed by the corresponding 85 data, but these 85 data are stored in a one-dimensional array. Therefore, if you want to find the corresponding 85 respectively, you need to multiply 85 by each thread
The corresponding starting point. Think about it
*/
float* pitem = predict + (5 + num_classes) * position;
/*
After obtaining the 85 (5 + 80) data starting position of the corresponding point of each thread, extract the corresponding data respectively, and objectness is the object obj confidence
*/
float objectness = pitem[4];
/* If it is less than the set obj confidence threshold, the thread returns */
if(objectness < confidence_threshold)
return;
/* After class_confidence is the confidence of the category. Because it is 80 categories, it loops 80 times */
float* class_confidence = pitem + 5;
float confidence = *class_confidence++;
int label = 0;
/* for The purpose of the loop is to get the category with the highest probability among the 80 categories */
for(int i = 1; i < num_classes; ++i, ++class_confidence){
if(*class_confidence > confidence){
confidence = *class_confidence;
label = i;
}
}
/* This is the loss during training, which is multiplied by two confidence levels, one is obj confidence, the other is category confidence */
confidence *= objectness;
/* If the total confidence is still less than the threshold, return directly */
if(confidence < confidence_threshold)
return;
/* On the contrary, it indicates that the forecast is valid and relevant data need to be retained */
int index = atomicAdd(parray, 1);
if(index >= max_objects)
return;
/* The first four data of the current 85 are actually cx, cy, width and height */
float cx = *pitem++;
float cy = *pitem++;
float width = *pitem++;
float height = *pitem++;
/* Convert to upper left corner coordinate point and lower right corner coordinate point at the same time */
float left = cx - width * 0.5f;
float top = cy - height * 0.5f;
float right = cx + width * 0.5f;
float bottom = cy + height * 0.5f;
/* The following is an affine inverse transformation to the coordinates under the original picture */
affine_project(invert_affine_matrix, left, top, &left, &top);
affine_project(invert_affine_matrix, right, bottom, &right, &bottom);
/*
* NUM_BOX_ELEMENT Is to limit the size of the largest bbox
*/
float* pout_item = parray + 1 + index * NUM_BOX_ELEMENT;
*pout_item++ = left;
*pout_item++ = top;
*pout_item++ = right;
*pout_item++ = bottom;
*pout_item++ = confidence;
*pout_item++ = label;
*pout_item++ = 1; // 1 = keep, 0 = ignore
}
static __device__ float box_iou(
float aleft, float atop, float aright, float abottom,
float bleft, float btop, float bright, float bbottom
){
float cleft = max(aleft, bleft);
float ctop = max(atop, btop);
float cright = min(aright, bright);
float cbottom = min(abottom, bbottom);
float c_area = max(cright - cleft, 0.0f) * max(cbottom - ctop, 0.0f);
if(c_area == 0.0f)
return 0.0f;
float a_area = max(0.0f, aright - aleft) * max(0.0f, abottom - atop);
float b_area = max(0.0f, bright - bleft) * max(0.0f, bbottom - btop);
return c_area / (a_area + b_area - c_area);
}
static __global__ void fast_nms_kernel(float* bboxes, int max_objects, float threshold){
/* The maximum number of open threads is 1024, but it is actually less than 1024. Therefore, the following processing is performed */
int position = (blockDim.x * blockIdx.x + threadIdx.x);
/* Minimum number of threads removed and actual bbox */
int count = min((int)*bboxes, max_objects);
if (position >= count)
return;
/* Normally, the array should be indexed from 0, but it is stored as float* pout_item = parray + 1 + index * NUM_BOX_ELEMENT;
* Therefore, the data should also be retrieved in this way. First, take a group of data as pccurrent and compare it with other bbox,
If the confidence is greater than the current value, it needs to be judged through iou
*/
// left, top, right, bottom, confidence, class, keepflag
float* pcurrent = bboxes + 1 + position * NUM_BOX_ELEMENT;
for(int i = 0; i < count; ++i){
float* pitem = bboxes + 1 + i * NUM_BOX_ELEMENT;
/* If you are comparing the same set of data or different types of data, skip the current bbox */
if(i == position || pcurrent[5] != pitem[5]) continue;
/* On the contrary, if the same bbox is not processed, continue to process downward. If the confidence of the project is greater than the current confidence, continue to process. On the contrary, skip */
if(pitem[4] >= pcurrent[4]){
/* If the confidence is the same, skip directly */
if(pitem[4] == pcurrent[4] && i < position)
continue;
/* If the confidence is greater than the current confidence, it is further processed through iou */
float iou = box_iou(
pcurrent[0], pcurrent[1], pcurrent[2], pcurrent[3],
pitem[0], pitem[1], pitem[2], pitem[3]
);
/* If the calculated iou is greater than the threshold value, the current bbox will be invalidated, and vice versa */
if(iou > threshold){
pcurrent[6] = 0; // 1=keep, 0=ignore
return;
}
}
/* Finally, it can be determined through the status of bboxes[6] */
}
}
static void decode_kernel_invoker(float* predict, int num_bboxes, int num_classes, float confidence_threshold, float nms_threshold, float* invert_affine_matrix, float* parray, int max_objects, cudaStream_t stream){
/* The main parameter needed here is the passed in parameter num_bboxes is 25200, which is the output concat of three head s, as follows:
* B × 3 × 85 × 80 × 80 --> B × 3 × 80 × 80 × 85 --> B × 19200 × 85
B × 3 × 85 × 40 × 40 --> B × 3 × 40 × 40 × 85 --> B × 4800 × 85 ----> B × 25200 × 85
B × 3 × 85 × 20 × 20 --> B × 3 × 20 × 20 × 85 --> B × 1200 × 85
It can be seen that it is the output exported by onnx. 25200 is the concat of three head s respectively, and each is the point of the characteristic graph. It needs to be emphasized here because the input
The picture is three channels, so it is 3 * 80 * 80. This must be understood. It corresponds to each two-dimensional position of the feature map. The storage method is one-dimensional, so it is necessary to get the data
Obtain data by calculation
*/
auto grid = grid_dims(num_bboxes);
auto block = block_dims(num_bboxes);
/* Through the above analysis, it can be found that each location needs to be calculated, so 25200 threads need to be opened */
/* If the kernel has wavy lines, it doesn't matter. It's normal. You just don't like it. Let's go to the decoding kernel */
checkCudaKernel(decode_kernel<<<grid, block, 0, stream>>>(predict, num_bboxes, num_classes, confidence_threshold, invert_affine_matrix, parray, max_objects));
/* For non maximum suppression, since 1024 bbox s are output at most during decoding, only 1024 threads are required to be enabled */
grid = grid_dims(max_objects);
block = block_dims(max_objects);
checkCudaKernel(fast_nms_kernel<<<grid, block, 0, stream>>>(parray, max_objects, nms_threshold));
}