Brain map: https://www.processon.com/mindmap/6179408f0e3e7416bdeb81d1

development environment

Mac C locale configuration

Software: Visual Studio Code

Coder Runner plug-in

1, Overview of data structures

1. Definition

How do we save a large number of complex problems in reality to the main memory (memory) with specific data types and specific storage structures, and the corresponding operations to realize a function (such as finding an element, deleting an element, and arranging all elements) on this basis, which is also called algorithm

Narrow sense:

Data structure is specialized in data storage

Data storage includes two aspects: individual storage + individual relationship storage

Generalized:

Data structure includes both data storage and data operation

The operation of storing data is an algorithm

Data structure = individual + individual relationship

Algorithm = operation on stored data

2. Algorithm

What is an algorithm?

Generalized: algorithms are operations on stored objects

Narrow sense: it refers to the methods and steps to solve the problem

Methods and steps of problem solving

How to measure the standard of the algorithm?

1. Time complexity: the approximate number of times the program needs to be executed, not the execution time

2. Space complexity: the maximum memory occupied during the execution of the algorithm

3. Degree of difficulty

4. Robustness

3. The status of data structures?

Data structure is the core course in software

Program = data storage + data operation + language that can be executed by computer

4. How many structures does data storage have?

1. Linear structure

• Continuous storage [array]

  • Advantages: fast storage speed

  • Disadvantages: slow insertion and deletion of elements

    Limited space

    You must know the length of the array in advance

    Large contiguous storage blocks are required

• Discrete storage [linked list]

  • Advantages: unlimited space
  • Disadvantages: slow storage speed

• Application of linear structure - [ stack ]

• Application of linear structure - [ queue ]

2. Nonlinear structure

• tree
• chart

2, Preparatory knowledge

1. Pointer

(1) The importance of pointer: the soul of C language

(2) . definition:

• Address:
  • Memory storage number (house number)
  • Nonnegative integer starting from 0
  • Range: 0 -- > fffffff [0-4G-1]
• Pointer:
  • The pointer is the address, and the address is the pointer
  • A pointer variable is a variable that stores the address of a memory unit
  • The essence of a pointer is a nonnegative integer with limited operation

2. Structure

(1) Why do structures appear?

In order to express some complex data, ordinary basic type variables can not meet the requirements, and the structure is born!

(2) What is a structure

Structure is a composite data type that can be defined by users according to our actual needs

(3) Precautions:

3. Dynamic memory allocation and release

3, Linear structure

What is linear structure?

All nodes can be connected by one line, otherwise it is a nonlinear structure (tree, graph)

1. Sequence table

(1) What is an array?

The elements are of the same type and of the same size

(2) Advantages and disadvantages of arrays?

Self created array

#include<stdio.h>
#include<mm_malloc.h>
#Include < stdlib. H > / / includes exit();
/*
    Analog array
*/

// A data type is defined. The name of the data type is struct Arr and contains three members: pBase, len and cnt
struct Arr{
    int *pBase; // Stores the address of the first element of the array
    int len; // The maximum number of elements that the array can hold
    int cnt; // The number of valid elements in the current array
};

/*
All statements
*/
void initArr(struct Arr *pArr, int length);
bool isEmpty(struct Arr *pArr); 
void showArr(struct Arr *pArr);
bool appendArr(struct Arr *pArr ,int val);
bool insertArr(struct Arr *pArr ,int pos,int val); 
bool isFull(struct Arr *pArr);
bool deleteArr(struct Arr *pArr ,int pos,int *pVal);
void inversionArr(struct Arr *pArr);
void softArr(struct Arr *pArr);

/*
Main function
*/
int main(){
    // int val;//  Used to receive the value of the deleted element
    struct Arr arr;  // Define a variable arr, which has no content at present
    initArr(&arr,6);
    // printf("%d\n",arr.len);
    // showArr(&arr);
    // printf("\n---------------------\n");

    // appendArr(&arr,1);
    // appendArr(&arr,2);
    // appendArr(&arr,3);
    // appendArr(&arr,4);
    // appendArr(&arr,5);
    // appendArr(&arr,6);
    // appendArr(&arr,7);
    // showArr(&arr);
    // printf("\n---------------------\n");
    // insertArr(&arr,6,99);
    // showArr(&arr);


    // Test deletear()
    // appendArr(&arr,1);
    // appendArr(&arr,2);
    // appendArr(&arr,3);
    // appendArr(&arr,4444);
    // appendArr(&arr,5);
    // appendArr(&arr,6);
    // showArr(&arr);
    // printf("\n---------------------\n");
    // deleteArr(&arr,4,&val); //  Val is the value used to accept the deleted data
    // printf("deleted element value is:% d\n",val);
    // showArr(&arr);


    // Implement inversion
    // appendArr(&arr,1);
    // appendArr(&arr,2);
    // appendArr(&arr,3);
    // appendArr(&arr,4);
    // appendArr(&arr,5);
    // appendArr(&arr,6);
    // inversionArr(&arr);
    // showArr(&arr);
    // printf("\n---------------------\n");

    
    // Implement ascending sort
    printf("\n---------------------\n");
    appendArr(&arr,2);
    appendArr(&arr,7);
    appendArr(&arr,5);
    appendArr(&arr,4);
    appendArr(&arr,8);
    appendArr(&arr,3);
    softArr(&arr);
    showArr(&arr);
    return 0;


}



/*
    initialization
*/
void initArr(struct Arr *pArr, int length){
    pArr->pBase = (int *)malloc(sizeof(int) * length); //pArr is the pBase in the structure variable to which the pointer variable points
    if(NULL == pArr->pBase){
        printf("Dynamic memory allocation failed!\n");
        exit(-1); // Terminate a program
    }else{
        pArr->len = length; // The maximum number of elements that the array can hold
        pArr->cnt = 0;
    }
    return;
}


/*
    display output
*/

void showArr(struct Arr *pArr){
    if(isEmpty(pArr)){
        printf("Array is empty\n");
    }else{
       for (int i = 0; i < pArr->cnt; i++)
       {
           printf("%d  ",pArr->pBase[i]); 
           printf("\n");
       }
    }
}


/*
    Determine whether the array is empty
*/
bool isEmpty(struct Arr *pArr){
    if (0 == pArr->cnt){
        return true;
    }else{
        return false;
    }
}



/*
    Add
*/
bool appendArr(struct Arr *pArr ,int val){
    // Cannot add when full
    if(isFull(pArr)){
        return false;
    }
    // When dissatisfied, you can add: 1. Process 2. Function 3. Trial and error
    pArr->pBase[pArr->cnt] = val;
    pArr->cnt++;
    return true;
}
/*
    Judge whether it is full
*/
bool isFull(struct Arr *pArr){
    if(pArr->len  == pArr->cnt){
        printf("already expired\n");
        return true;
    }else{
        return false;
    }
}

bool insertArr(struct Arr *pArr ,int pos,int val){
    // 1. Judge whether it is full. If it is full, it cannot be inserted
    if(isFull(pArr)){
        return false;
        
    }
    // 2. Then judge whether it crosses the boundary
    if(pos <1 || pos>pArr->cnt+1){

        return false;
    }

    for(int i = pArr->cnt-1; i>=pos-1; i--){
        pArr->pBase[i+1] = pArr->pBase[i]; // Give the last one to the next one
    }
    pArr->pBase[pos-1] = val; // insert
    pArr->cnt++; // Effective number plus 1
    return true;
}

bool deleteArr(struct Arr *pArr ,int pos,int *pVal){
    if(isEmpty(pArr)){
        printf("Array is empty\n");
        return false;
    }
    if(pos<1 && pos>pArr->cnt){
        printf("Range exception");
        return false;
    }

    // Find this value first
    *pVal = pArr->pBase[pos-1];
    // Start deletion
    for(int i = pos; i<pArr->cnt; i++){
        pArr->pBase[i-1] = pArr->pBase[i];
    }
    pArr->cnt--;// Effective number minus 1
    return true;
}

void inversionArr(struct Arr *pArr){
    int i=0; //first
    int j=pArr->cnt-1; // the last one
    int temp;
    while (i<j) // Value exchange
    {   
        temp = pArr->pBase[i];
        pArr->pBase[i] = pArr->pBase[j];
        pArr->pBase[j] = temp;
        i++;
        j--;
    }
    return;
 
}

void softArr(struct Arr *pArr){
    // Select sort
    int temp;
    for(int i =0; i<pArr->cnt; i++){
        for(int j=i+1; j<pArr->cnt;j++){
            if(pArr->pBase[i]>pArr->pBase[j]){
                temp = pArr->pBase[i];
                pArr->pBase[i] = pArr->pBase[j];
                pArr->pBase[j] = temp;
            }
        }
    }



}

2. Linked list

Preliminary knowledge typedef keyword

Objective: knock on the linked list by hand

1,

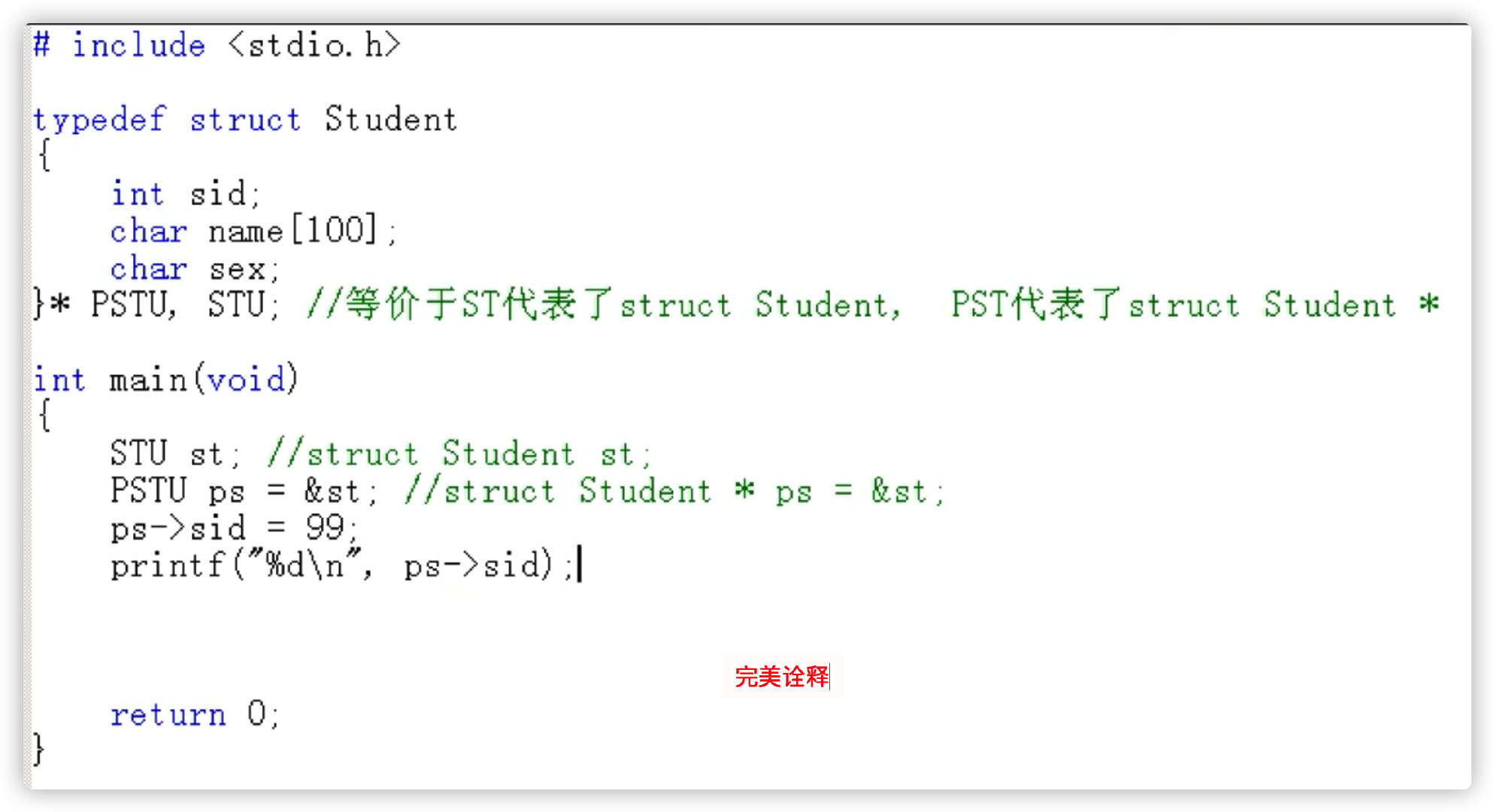
#include<stdio.h>
typedef int QQ;  //Give int a new name int = QQ
typedef struct Student{
    int sid;
    char name[100];
    char sex;
}St; // St is equivalent to struct Student

int main(){
    int i = 10;
    QQ j = 10; // QQ is equivalent to int
    printf("%d %d",i,j);
    struct Student st;
    struct Student *ss;

    St st; // St st is equivalent to struct Student st;
    St *ss; // St *ss is equivalent to struct Student *ss;
    return 0;
}

2,

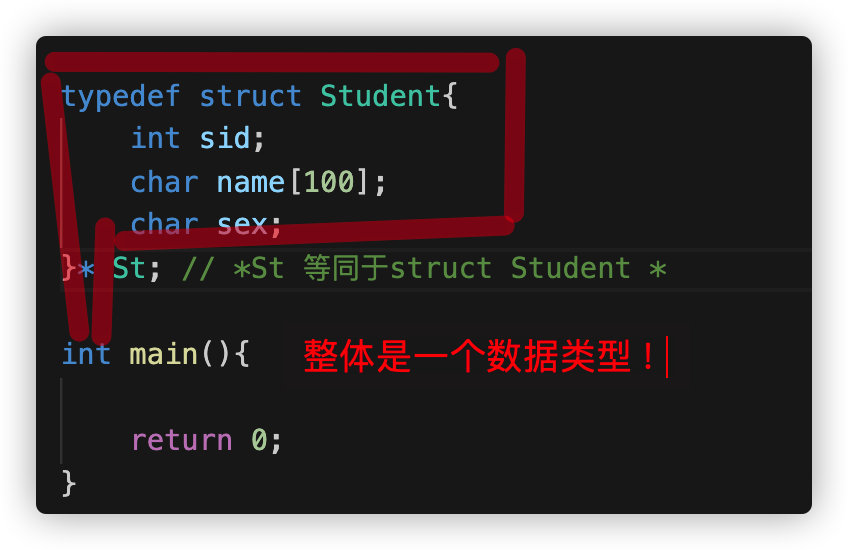
#include<stdio.h>

typedef struct Student{
    int sid;
    char name[100];
    char sex;
}*St; // *St is equivalent to struct Student*

int main(){   
    return 0;
}

3,

(1) Definition

1. N nodes discrete

2. Each other through the pointer necklace

3. Each node can only have one precursor node, and there can only be one follower node behind each node. The receiving node has no predecessor node, and the tail node has no follower node

Technical Term:

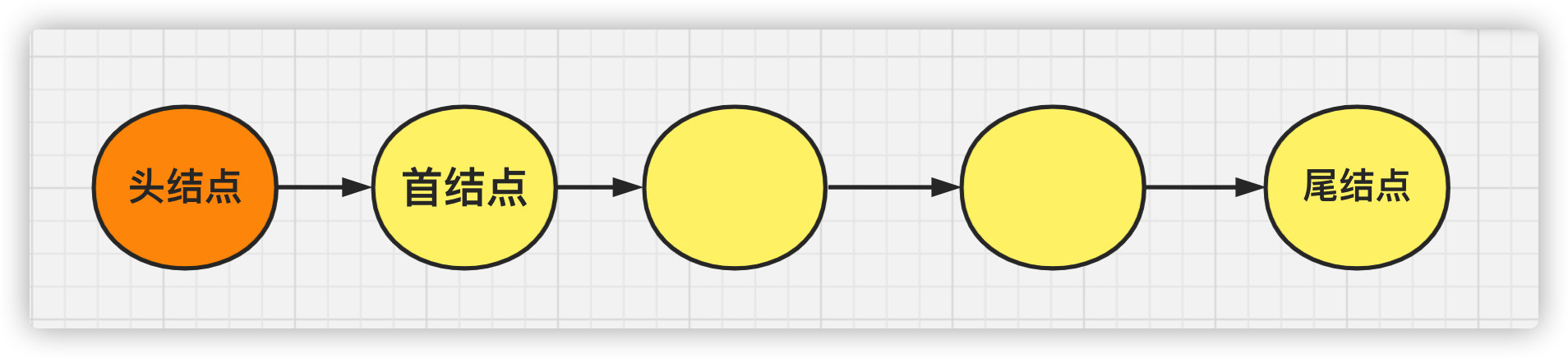
**First node: * * first valid node

**Tail node: * * last valid node

Head node: the node before the first valid node

The header node does not store valid data

The purpose of header node is to facilitate the operation of linked list

The data type of the header node is the same as that of the header node

**Header pointer: * * pointer variable pointing to the header node

**Tail pointer: * * pointer variable pointing to the tail node

How many parameters do we need to determine a linked list????

Only one parameter is needed: the header pointer, because we can calculate all the other information of the linked list through the header pointer

(2) Classification

1. Single linked list

2. Double linked list: each node has two pointers

3. Circular linked list: all other nodes can be found through any node

4. Acyclic linked list:

(3) Algorithm

The algorithm has two standards, one is broad and the other is narrow. In a narrow sense, the algorithm is related to the storage of data. In a broad sense, then

It's irrelevant.

Generic:

The effect of using a certain technology is that different storage methods perform the same operations

Note: there are differences between narrow sense and broad sense

• Narrow sense: from the internal real realization
• Generalized:

How to learn algorithms?

Related to mathematics, take out the answer and understand the answer!

How to change a program (answer) from not understanding to understanding?

• technological process
• Function of each statement
• Trial and error

1. Traversal

2. Search

3. Empty

4. Destroy

5. Find length

6. Sort

7. Delete node

...

Self created linked list

#include<stdio.h>
#include<mm_malloc.h>

typedef struct Node{
    int data; //Data domain
    struct Node *pNext;
}NODE,*PNODE;

//Declarative function
PNODE create_list();
void traverse_list(PNODE pHead);
bool is_empty(PNODE pHead);
int getLenght(PNODE pHead);
bool insert_list(PNODE pHead,int pos,int val);
bool deleteList(PNODE pHead,int pos,int *val); // The third parameter is used to store the value of the deleted linked list
void softList(PNODE pHead); //sort
bool insertList(PNODE pHead,int pos,int val); //Linked list insertion, pos starts from 1
bool deleteList(PNODE pHead,int pos,int *pVal); 

int main(){
    PNODE pHead = NULL; //  Equivalent to struct Node *pHead = NULL;
    pHead = create_list(); //create_list() function: create an acyclic single linked list and assign the address of the head node of the linked list to pHead
    traverse_list(pHead);//traverse_list traversal output
    if (is_empty(pHead))
    {
        printf("The linked list is empty!\n");
    }else{
        printf("Linked list is not empty!\n");
    }
    int len = getLenght(pHead);
    printf("The length of the linked list is:%d\n",len);

    printf("\n-------------\n");

    //Test sequencing
    // softList(pHead);
    // traverse_list(pHead);


    printf("\n-------------\n");
    //Test insertion
    // insertList(pHead,4,520);
    // traverse_list(pHead);

    printf("\n-------------\n");
    //Test delete
    int val;
    
    if (deleteList(pHead,4,&val))
    {
        printf("Deletion succeeded. The value of this element is:%d\n",val);
    }else{
        printf("Deletion failed. The deleted element does not exist\n");
    }
    traverse_list(pHead);
    return 0;



}

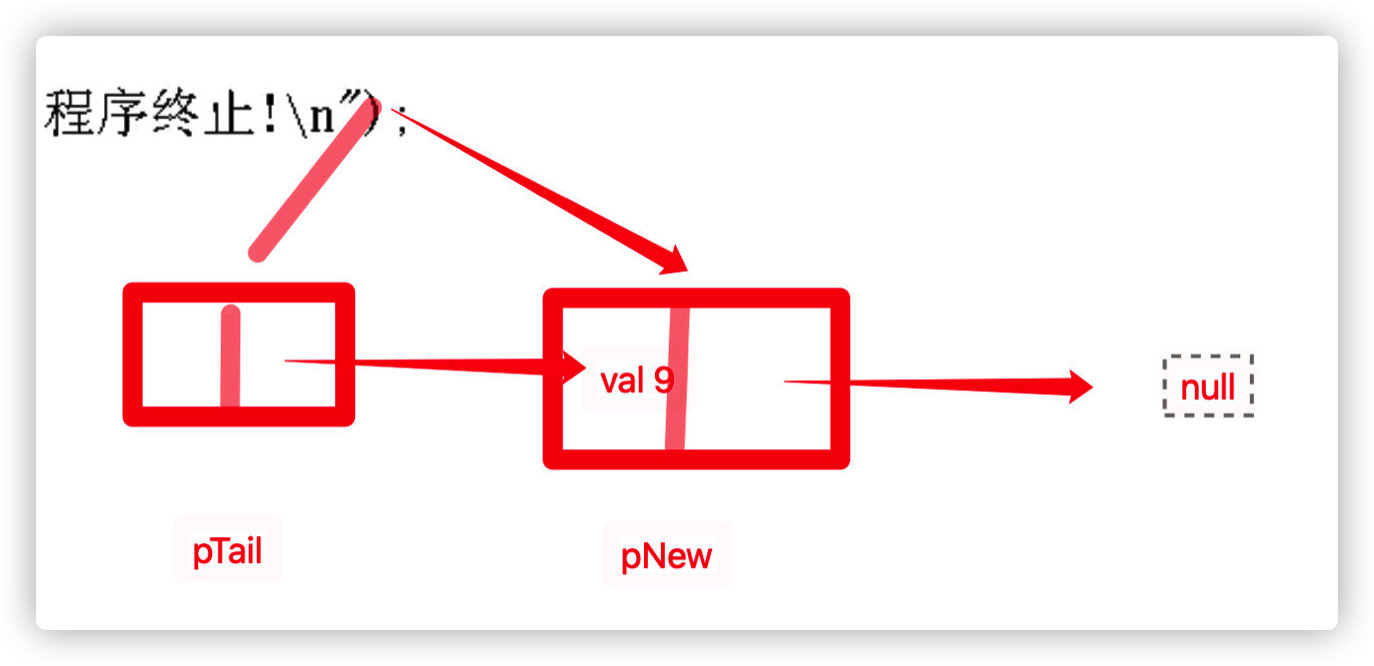
PNODE create_list(){
    // A header node that does not store valid data is allocated
    PNODE pHead =  (PNODE)malloc(sizeof(NODE));//  
    if(NULL == pHead){
        printf("Allocation failed, program terminated!");
        exit(-1);
    }

    PNODE pTail = pHead;
    pTail->pNext = NULL;


    int len;
    int i; // Used to store the number of valid user input nodes
    int val; // It is used to temporarily store the value of the node entered by the user
    printf("Please enter the number of nodes you need to generate the linked list:len=");
    scanf("%d",&len);
    for(i=0; i<len; i++){
        printf("Please enter page%d Values for nodes:",i+1);
        scanf("%d",&val);
        PNODE pNew = (PNODE)malloc(sizeof(NODE));
        if(NULL == pHead){
            printf("Allocation failed, program terminated!");
            exit(-1);
       }
       pNew->data=val;
    //    How to hang the generated node to the pahead header pointer? The method is as follows
        pTail->pNext = pNew;
        pNew->pNext = NULL;
        pTail = pNew;//  pTail points to the address of the structure object where pNew will be located
    }
    return pHead;
}

void traverse_list(PNODE pHead){
    // Traversal output
    PNODE p = pHead->pNext;
    while (p!= NULL)
    {

        printf("%d ",p->data);
        p = p->pNext;
    }
    printf("\n");
    return;
}

bool is_empty(PNODE pHead){
    if (pHead->pNext==NULL)
    {
        return true;
    }else{
        return false;
    }
    
}


int getLenght(PNODE pHead){
    int len = 0;
    // Traversal output
    PNODE p = pHead->pNext;
    while (p!= NULL)
    {

        len++;
        p = p->pNext;
    }
    return len;  
}

// bool insert_list(PNODE pHead,int pos,int val);

 //Bubble sorting
 /*
 
 */
void softList(PNODE pHead){
    int i,j;
    int temp;
    int len =getLenght(pHead);
    PNODE p,q;
    for (i=0,p=pHead->pNext; i<len-1; i++,p=p->pNext) // Outer loop, 6 numbers, only need to compare 5 times
    {
        for(j=i+1,q=p->pNext; j<len; j++,q=q->pNext){
            if(p->data>q->data){ //Class uses a [i] > a [J] in the array
                temp = p->data;
                p->data =q->data;
                q->data = temp;
            }
        }
    }
    return;
}

// Insert a new node before the pos node of the linked list pointed to by pHead. The value of this node is val, and the value of pos starts from 1
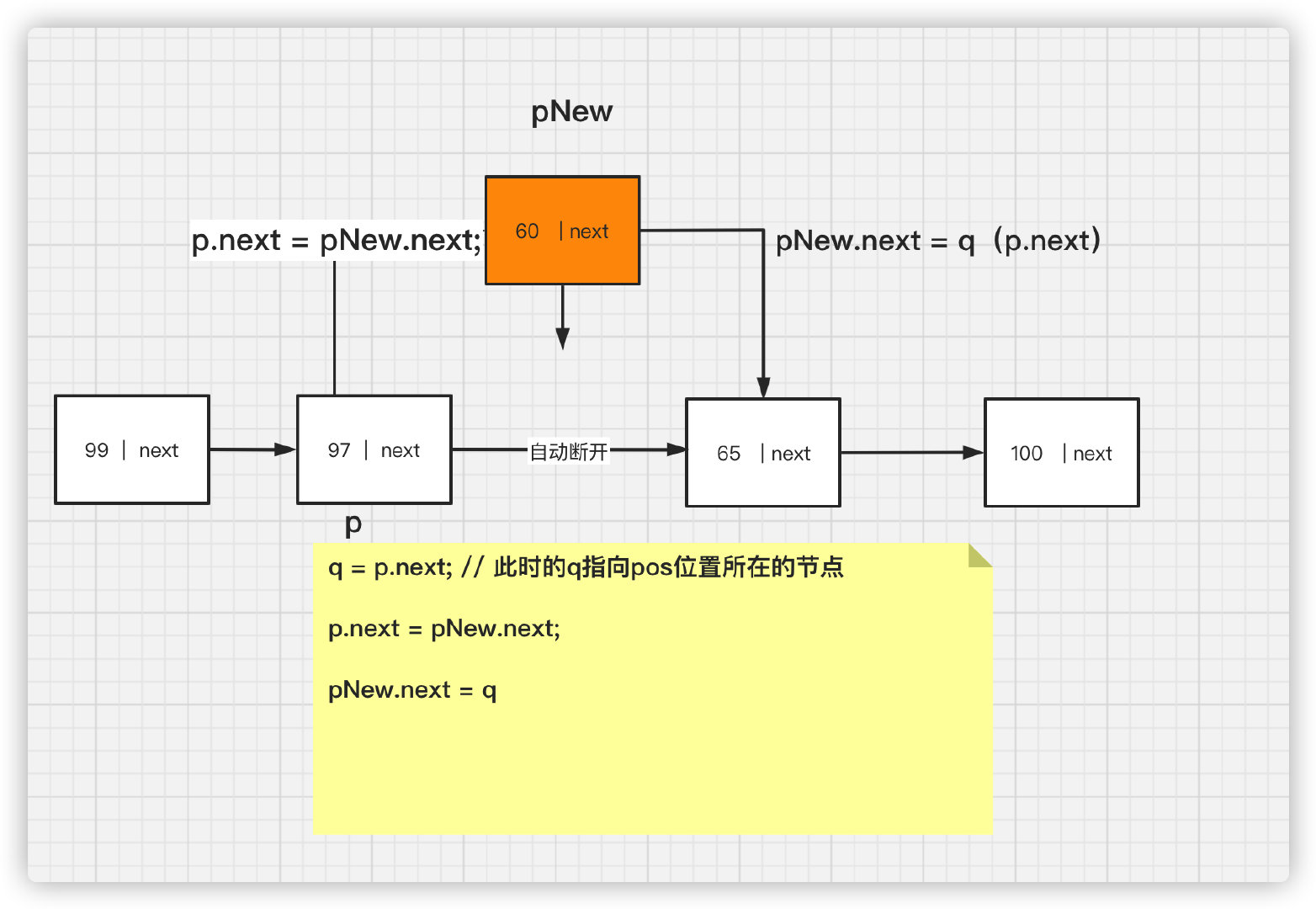
bool insertList(PNODE pHead,int pos,int val){
    //Is the scope of pos legal
    int i = 0;
    PNODE p = pHead;

    while (p!=NULL && i <pos-1) //The purpose of this loop is to make p point to the previous node of pos
    {
        p = p->pNext; // Eventually p will point to
        i++;
    }
    if (p==NULL || i >pos-1)
    {
       return false;
    }

    PNODE pNew =  (PNODE)malloc(sizeof(NODE));
    if(NULL == pNew){
        printf("Allocation failed, program terminated!");
        exit(-1);
    }
    pNew->data=val; //Value storage
    //Start insertion
    PNODE q = p->pNext; //q is an intermediate variable
    p->pNext = pNew;
    pNew->pNext=q;
    return true;
    /*
    The core code of these three behaviors - detailed analysis can be seen in the flow chart below
    PNODE q = p->pNext; //q Is an intermediate variable
    p->pNext = pNew;
    pNew->pNext=q;
    */
}


bool deleteList(PNODE pHead,int pos,int *pVal){
   
    //Is the scope of pos legal
    int i = 0;
    PNODE p = pHead;

    while (p->pNext!=NULL && i <pos-1) //The purpose of this loop is to make p point to the previous node of pos
    {
        p = p->pNext; // Eventually p will point to
        i++;
    }
    if (NULL==p->pNext || i >pos-1)
    {
       return false;
    }
    //Accept the value stored by the deleted node
    *pVal = p->pNext->data;
    //Start deletion
    PNODE q = p->pNext; // Save the element to be deleted first to free up space later
    p->pNext = p->pNext->pNext; // The so-called deletion is to point p to the next element to be deleted, and then release the space of p
    free(p);

}

Insert 3 lines of code analysis:

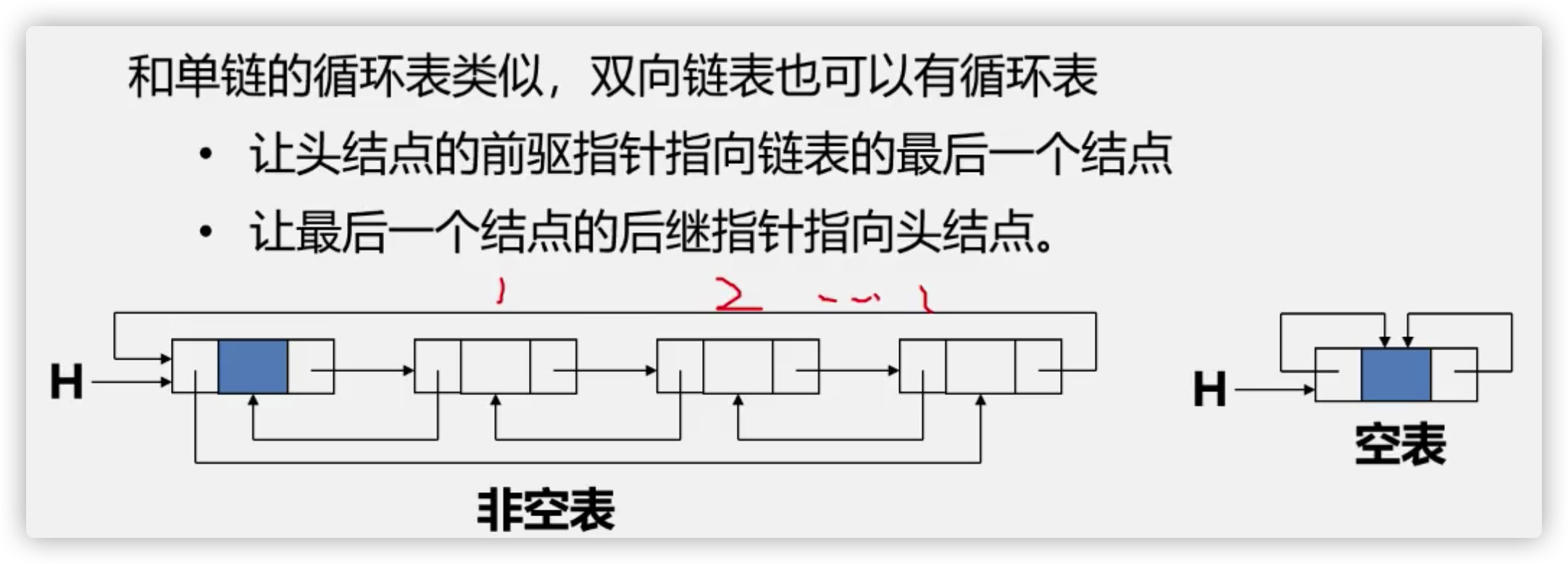
(4) Circular linked list

Definition: a linked list with head and tail (that is, the pointer field of the last node in the list points to the head node, and the whole linked list forms a ring)

==Advantages: = = starting from any node in the table, you can find other nodes in the table.

How to merge two circular linked lists with tail pointers?

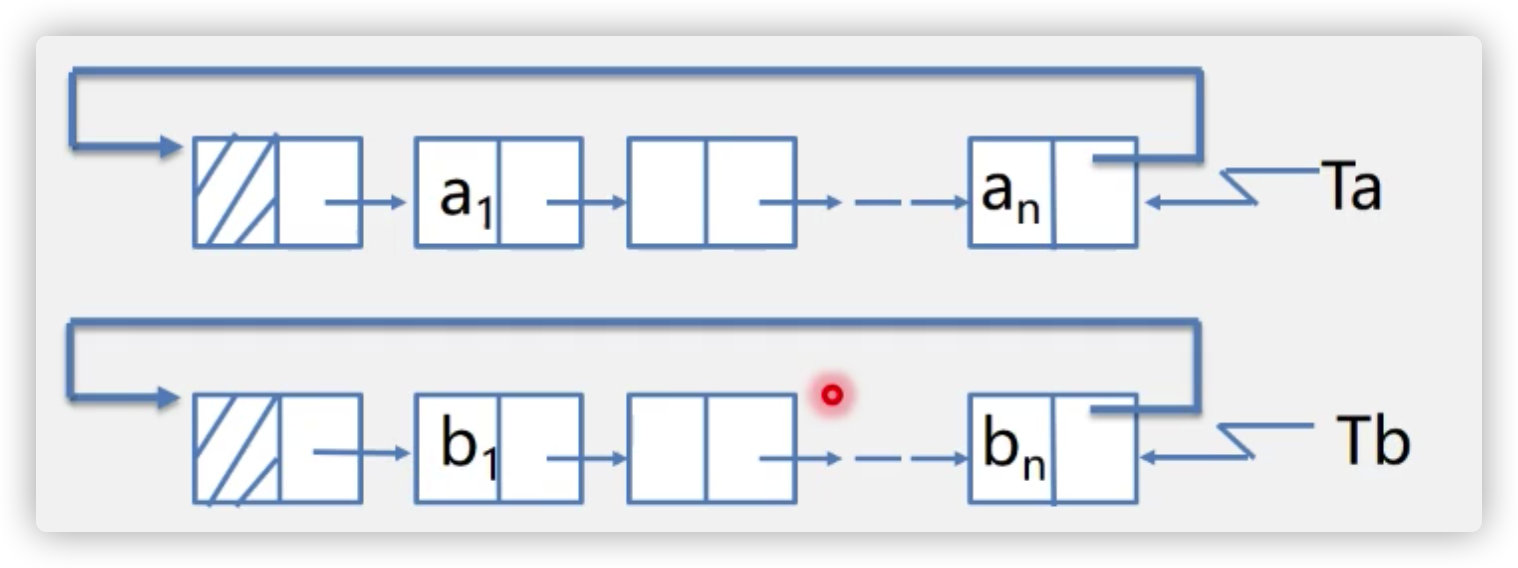
What are the operations?

(1) . keep the head node of Ta first: P = Ta - > next

(2) . connect the footer of Ta table to the first valid node of Tb table: Ta - > next = Tb - > next - > next;

(3) . release the header node of TB table: free (TB - > next); delete Tb->next;

(4) The tail node of Tb table points to the head node of Ta table: Tb - > next = P

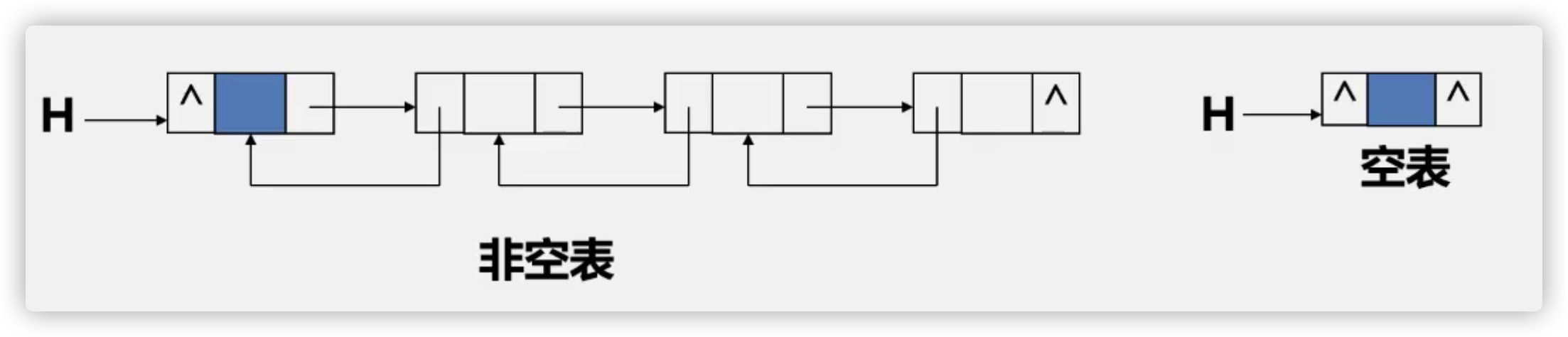
(5) Bidirectional linked list

1. Definition: add a pointer field prior to its direct precursor in each node of the single linked list. In this way, a chain with two different directions is formed in the linked list, so it is called a two-way linked list.

2. Structure:

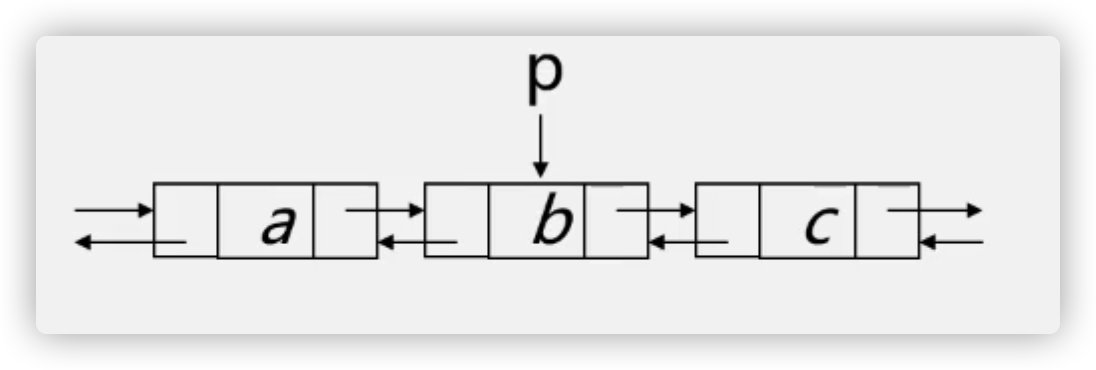
Insertion of bidirectional linked list

(6) Bidirectional circular linked list

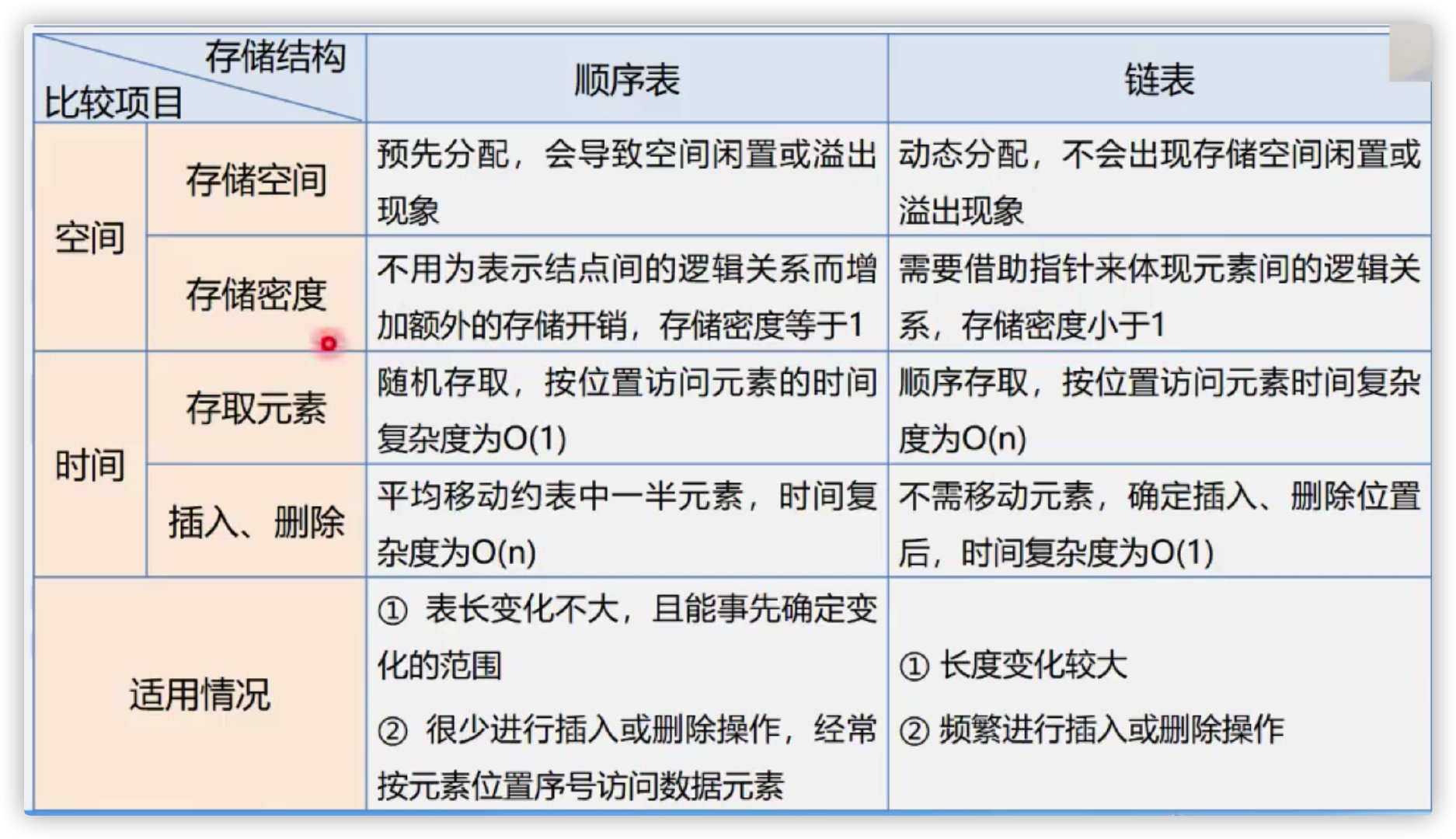
(7) Comparison between sequential list and linked list

1, Advantages and disadvantages of linked list:

advantage:

1. Node space can be dynamically applied for and released

2. Delete and insert operations only need to modify the pointer without moving the element

Disadvantages:

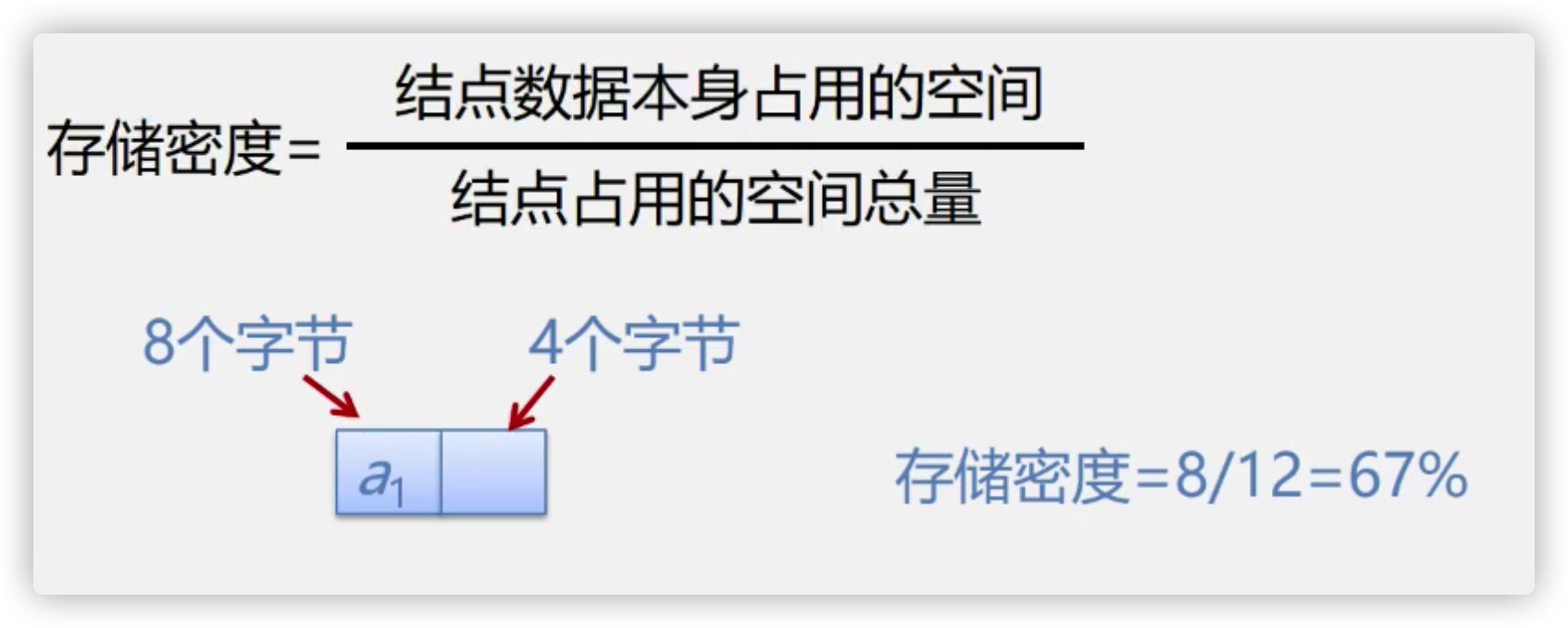
3. The storage density is low because each node needs to store the addresses of its subsequent nodes and precursor nodes while storing the data itself, which takes up a large space

4. Non random access structure, the time complexity is improved

What is random access?

That is, any element can be obtained through the following table

(8) Application of linear table

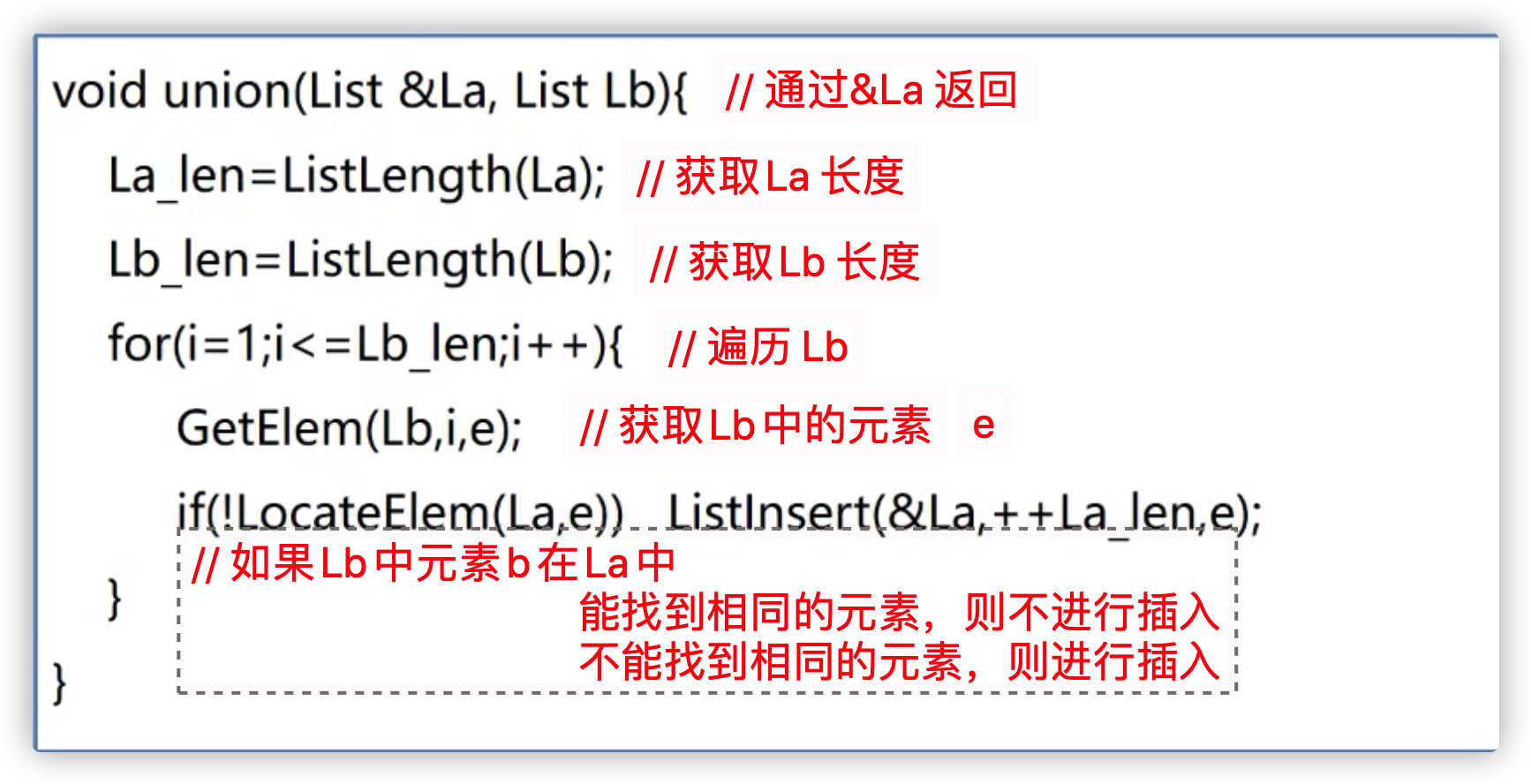
1. Merging of linear tables

Implementation method:

2. Merge of ordered linear tables

Why non decreasing ordering?

Because there may be duplicate elements

Sequential tables are used to merge sequential tables:

Linked list to achieve ordered table merging

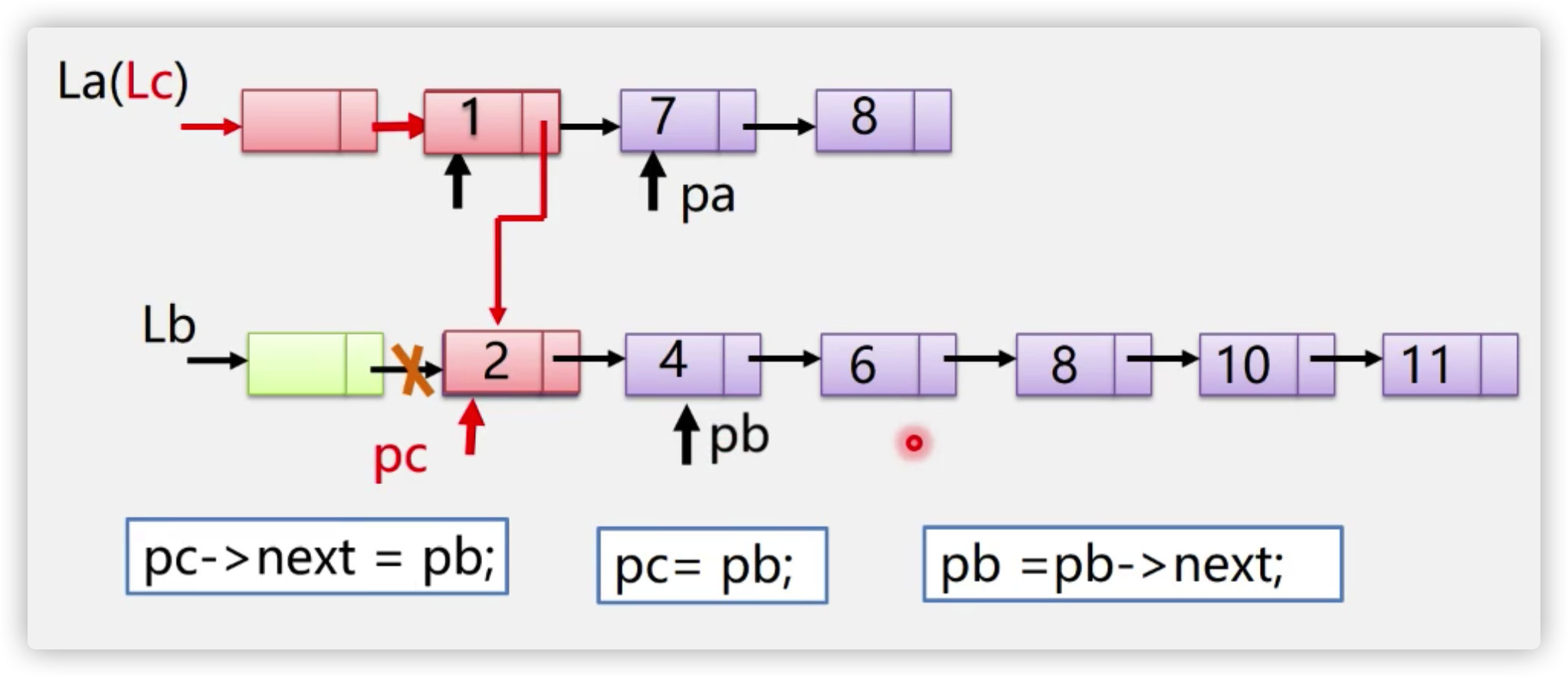
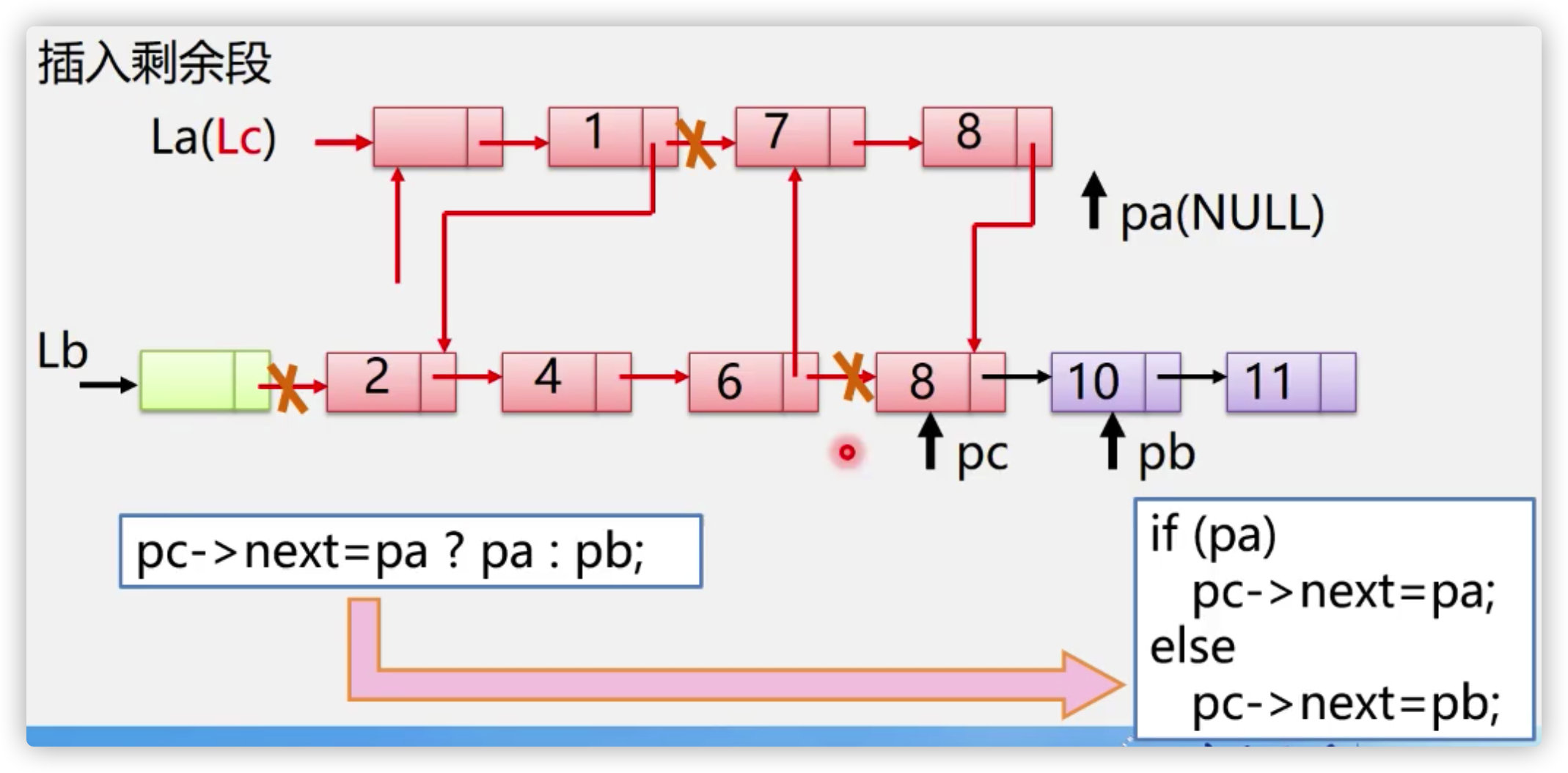
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-ntndse7k-1636095678603) (/ users / ouyangyansong / library / Application Support / typora user images / image-20211031151933666. PNG)]

Note: in the worst case, La is as long as Lb, and all must be executed. The maximum time complexity is 👆🏻

(9) Case 1: operation of univariate polynomial

(10) Case 2: operation of sparse polynomials

1. Sequential storage implementation

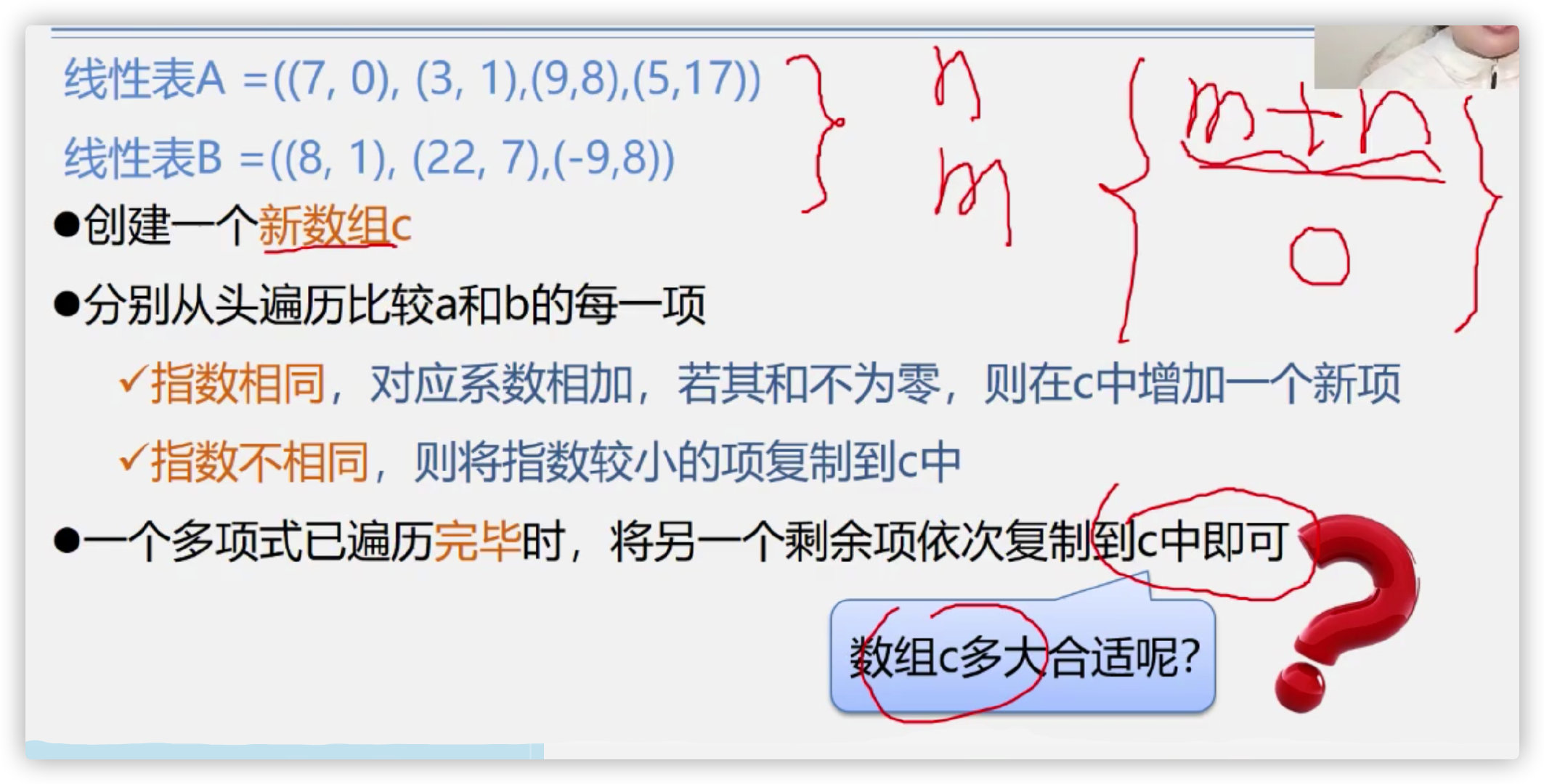
Problems with using sequential tables for storage:**==

1. It is not easy to determine how much space is allocated for storage, and the storage space allocation is not flexible

2. It is necessary to create a new array with high space complexity

How to solve the above problems?

Answer: use linked list for storage

2. Chain storage implementation

Create polynomial code

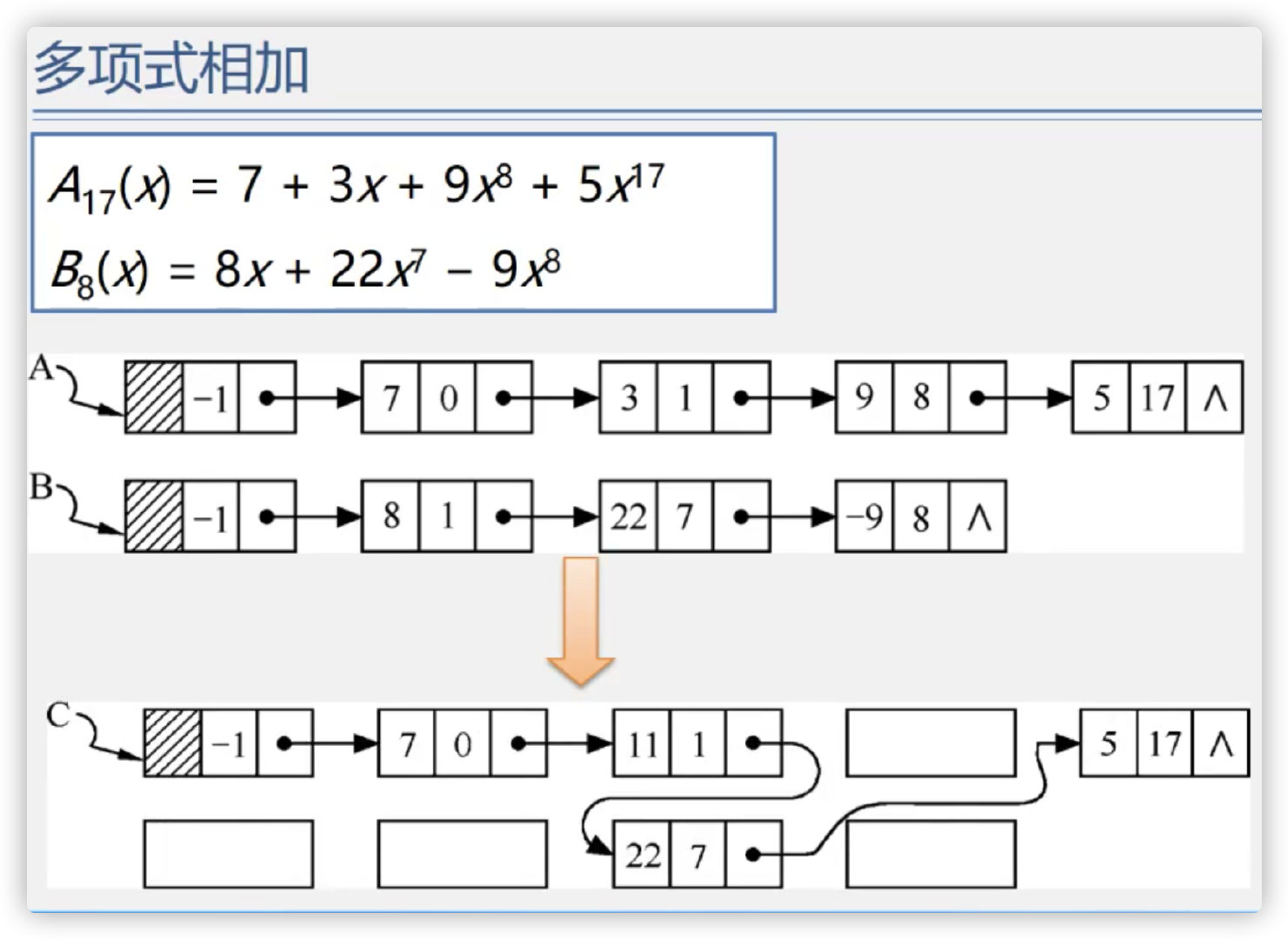
Polynomial addition algorithm

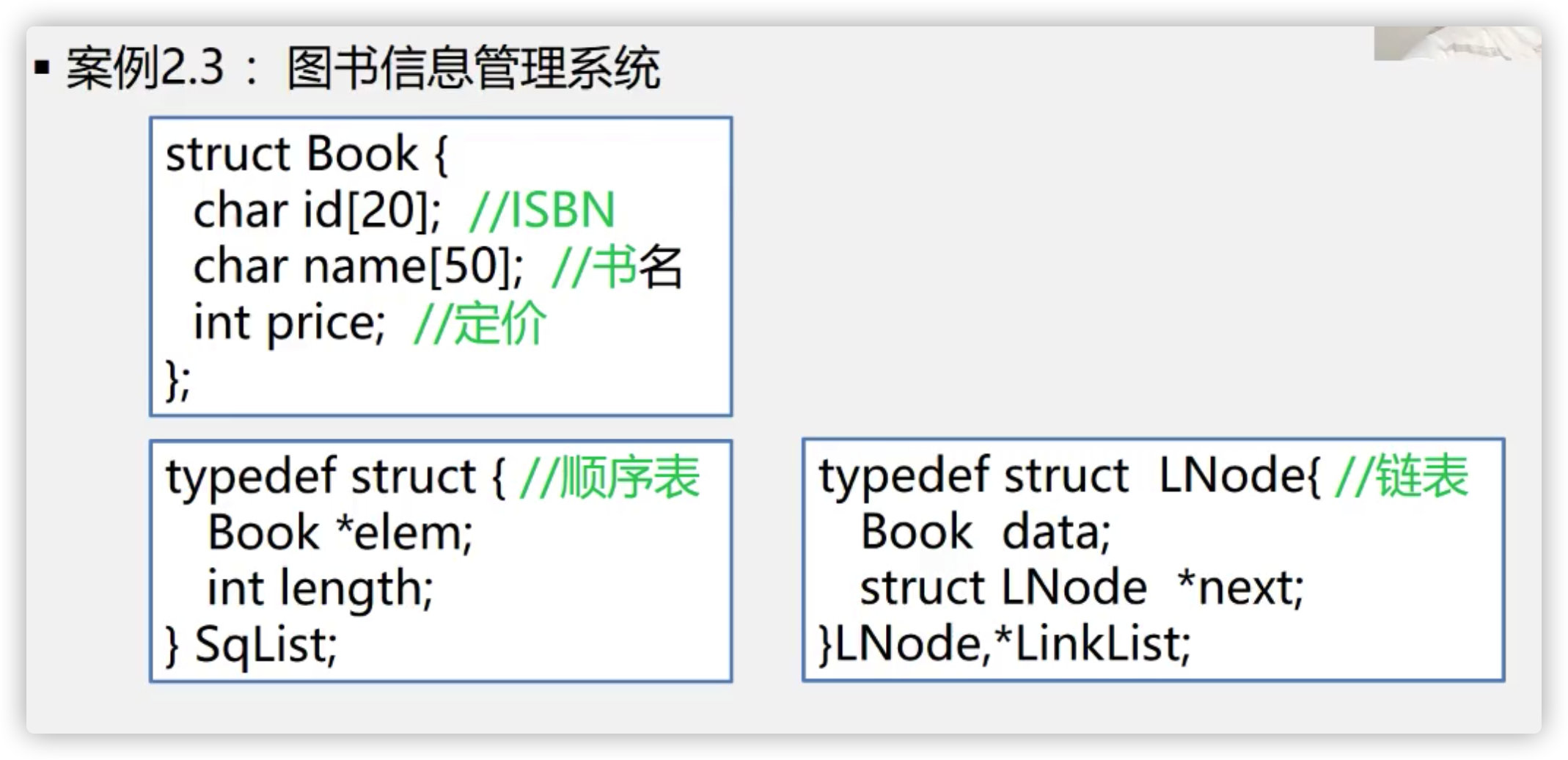
(11) Case 3: implementation of library management system

3. Stack

(1) Definition

A storage structure that can implement "first in first out" or "last in first out"

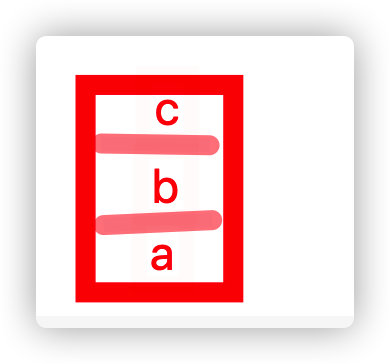
A: there can be no cab, because if c is on the stack, a and b must also be on the stack

Only possible: c-b-a

(2) Code implementation related algorithms

1. Implementation of sequential stack

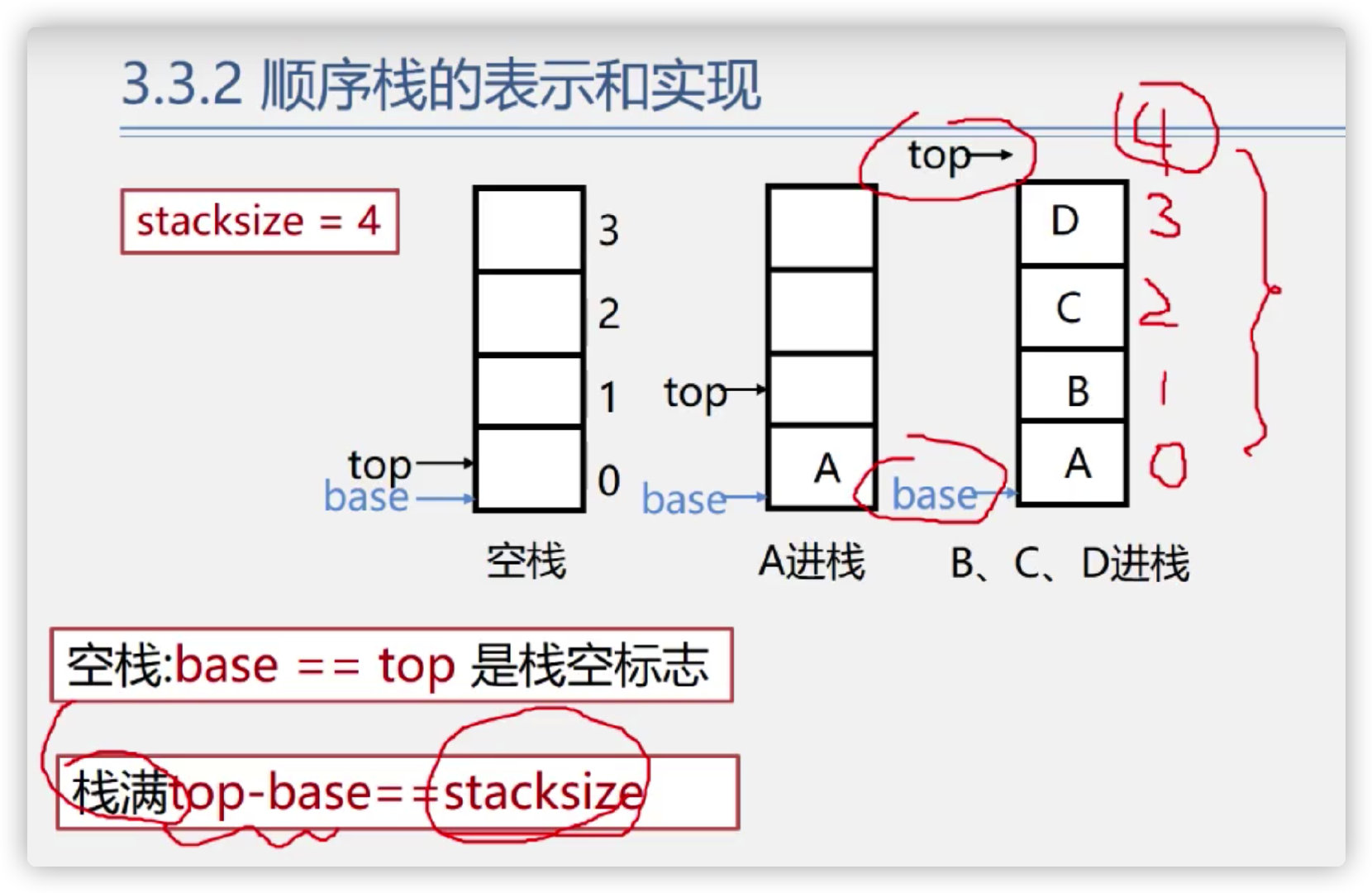
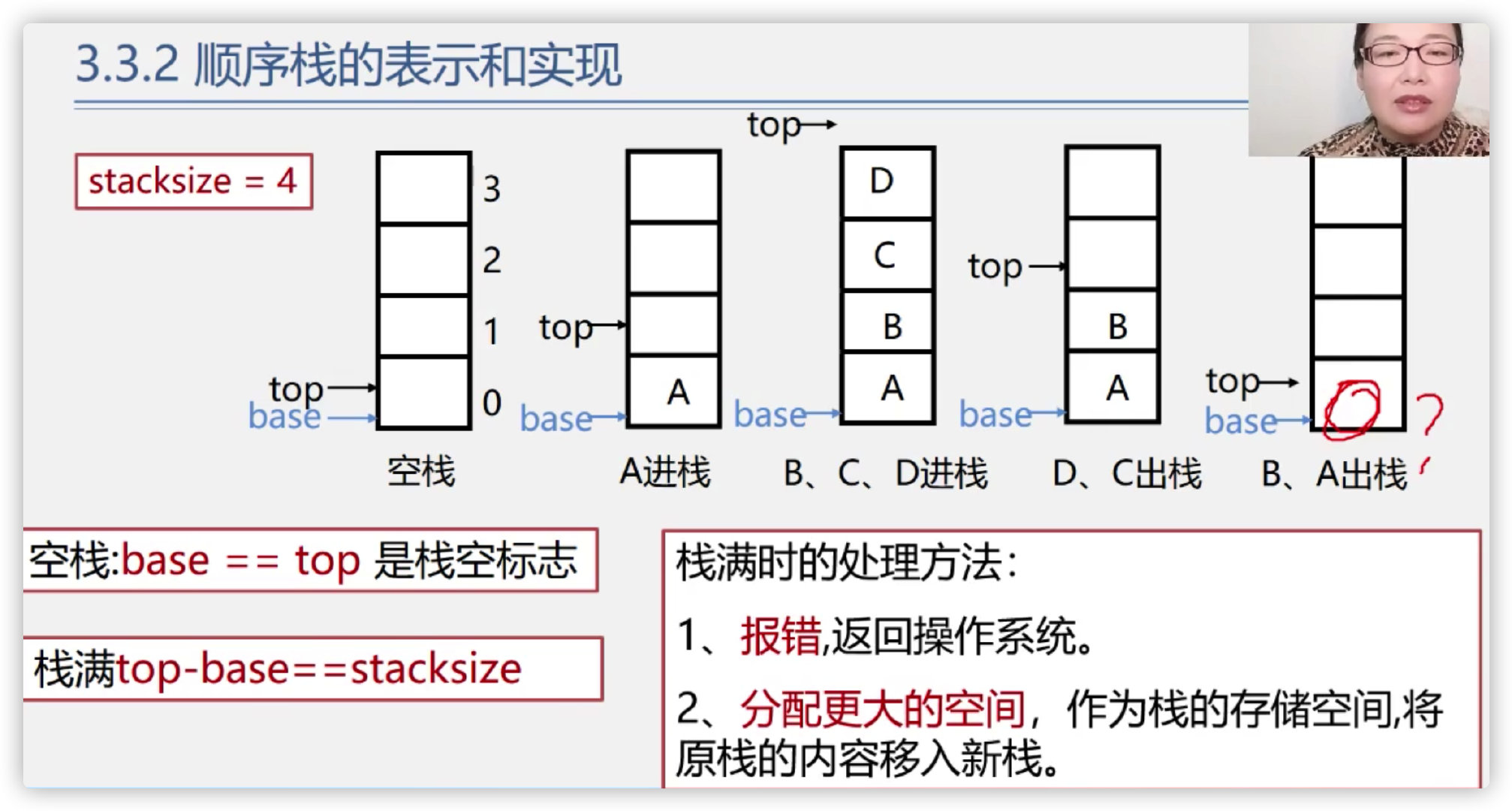
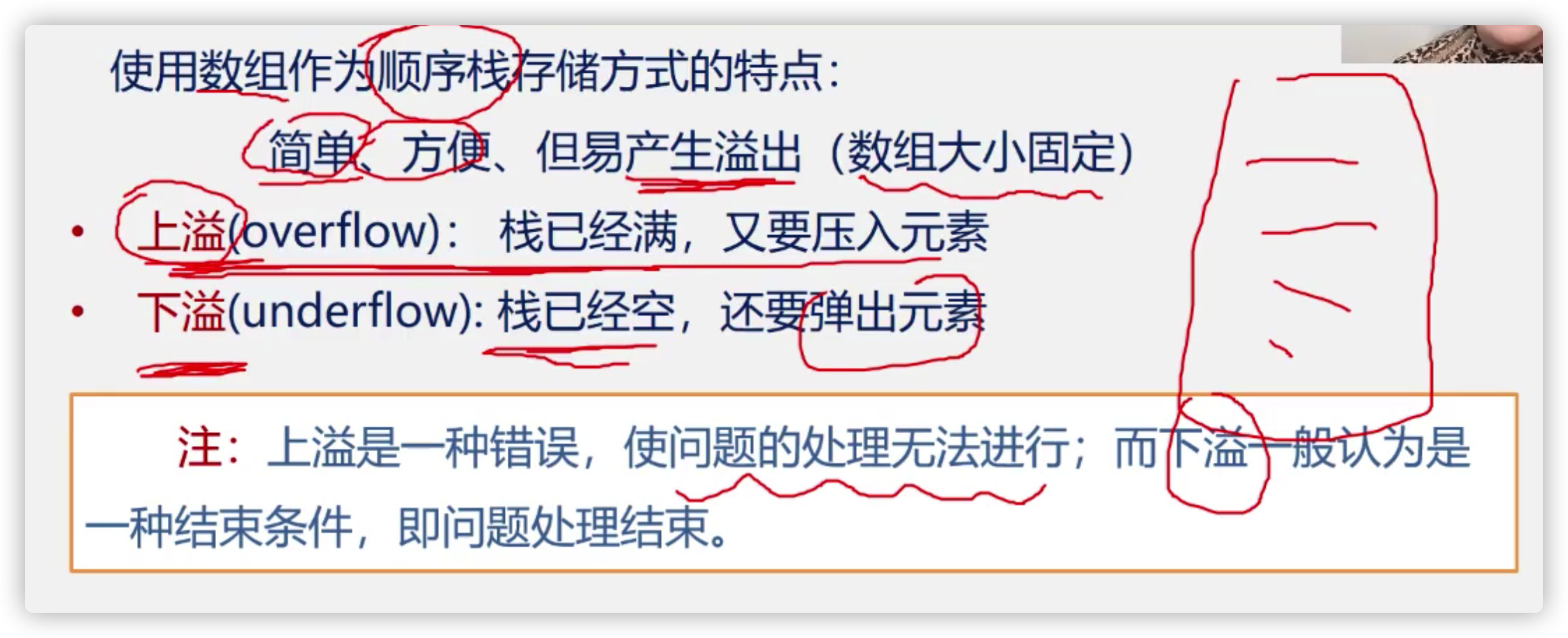
Code implementation of sequential stack

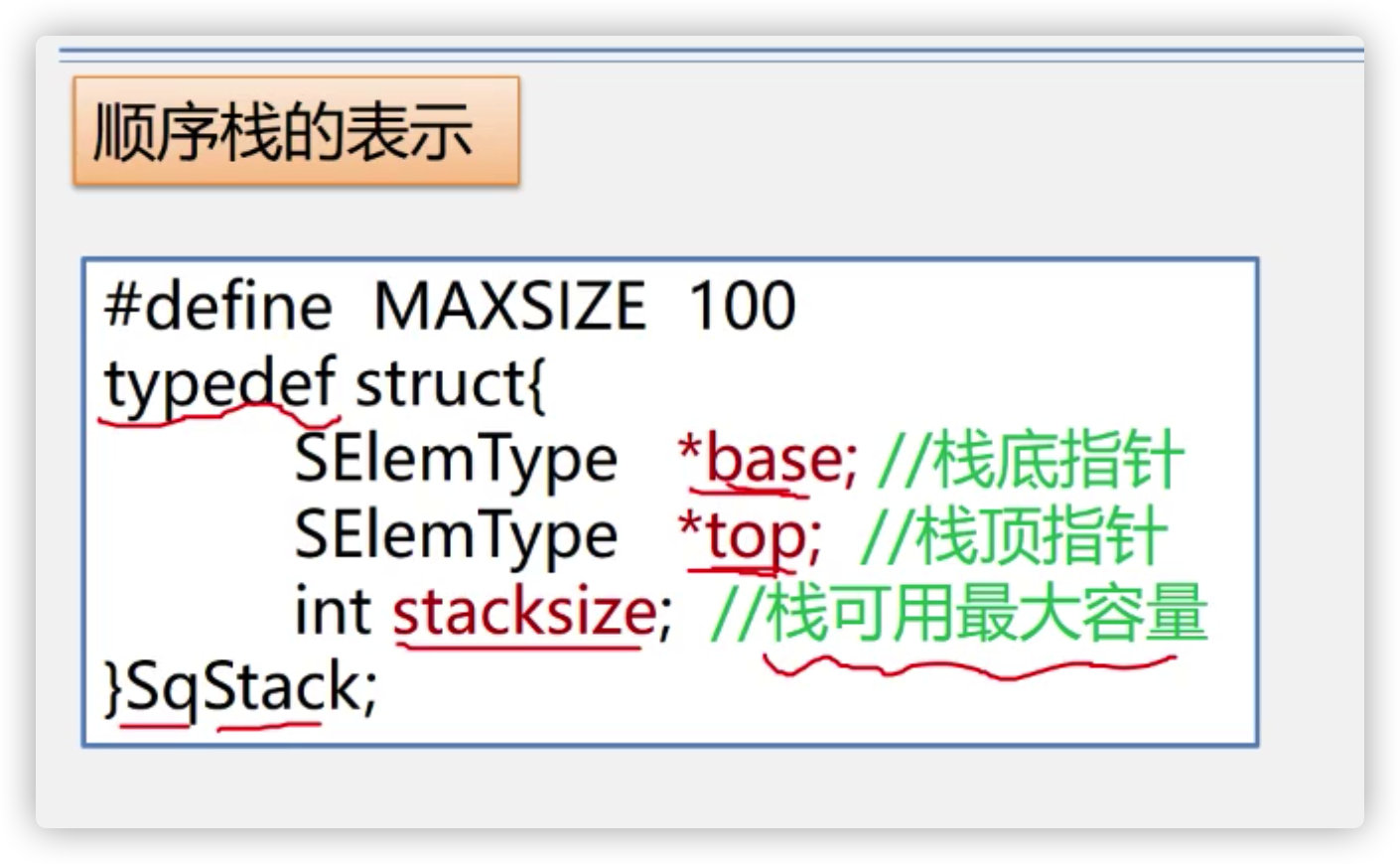
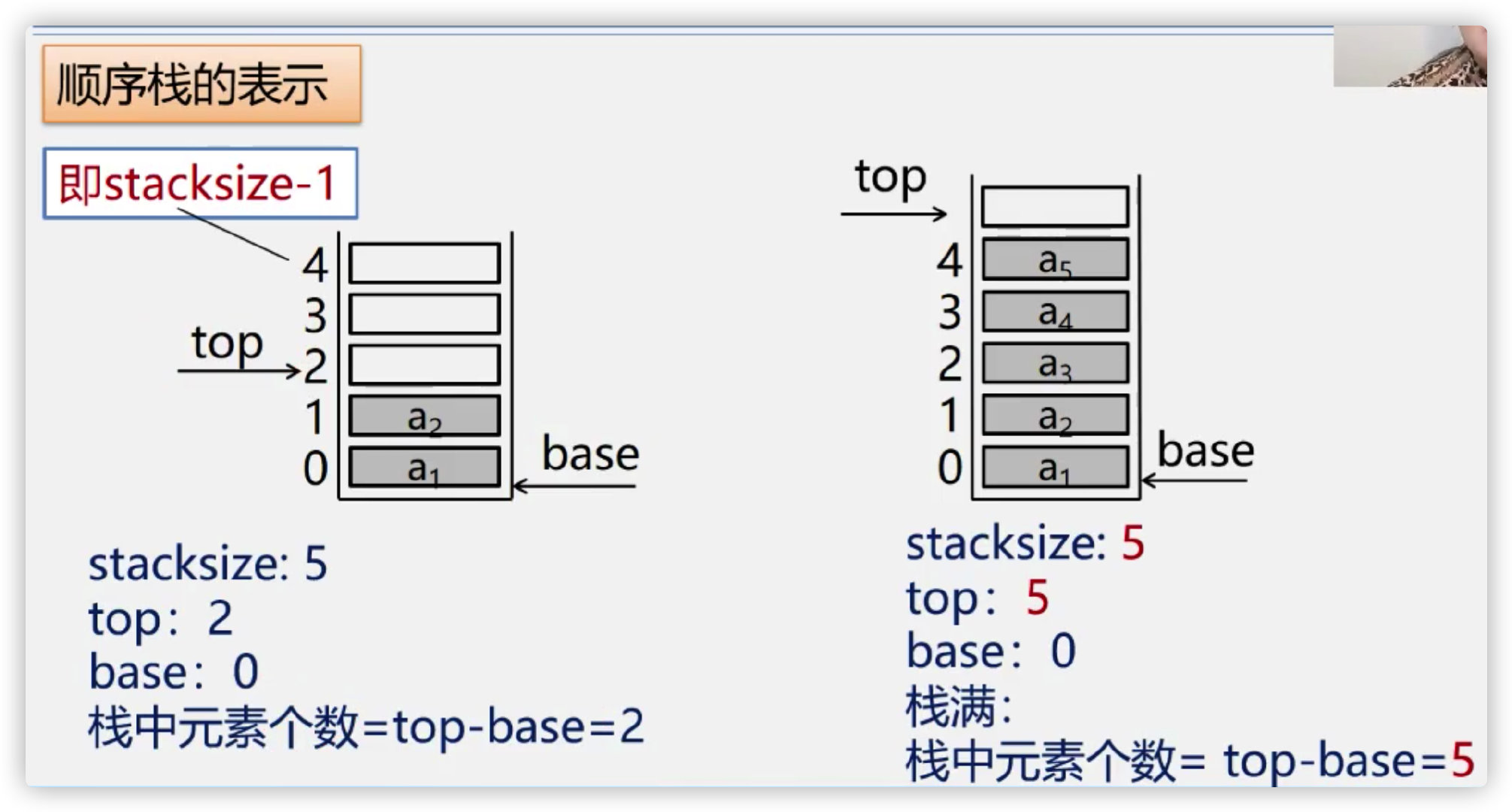
Initialization of sequential stack

Judge whether the sequence stack is empty

Find the length of sequential stack

Empty sequence stack

Note: the premise if(S.base) is to judge whether the stack is empty in advance. If it is already empty, it is not necessary to continue the following operations

Destruction of sequential stack

Sequential stacking / pressing

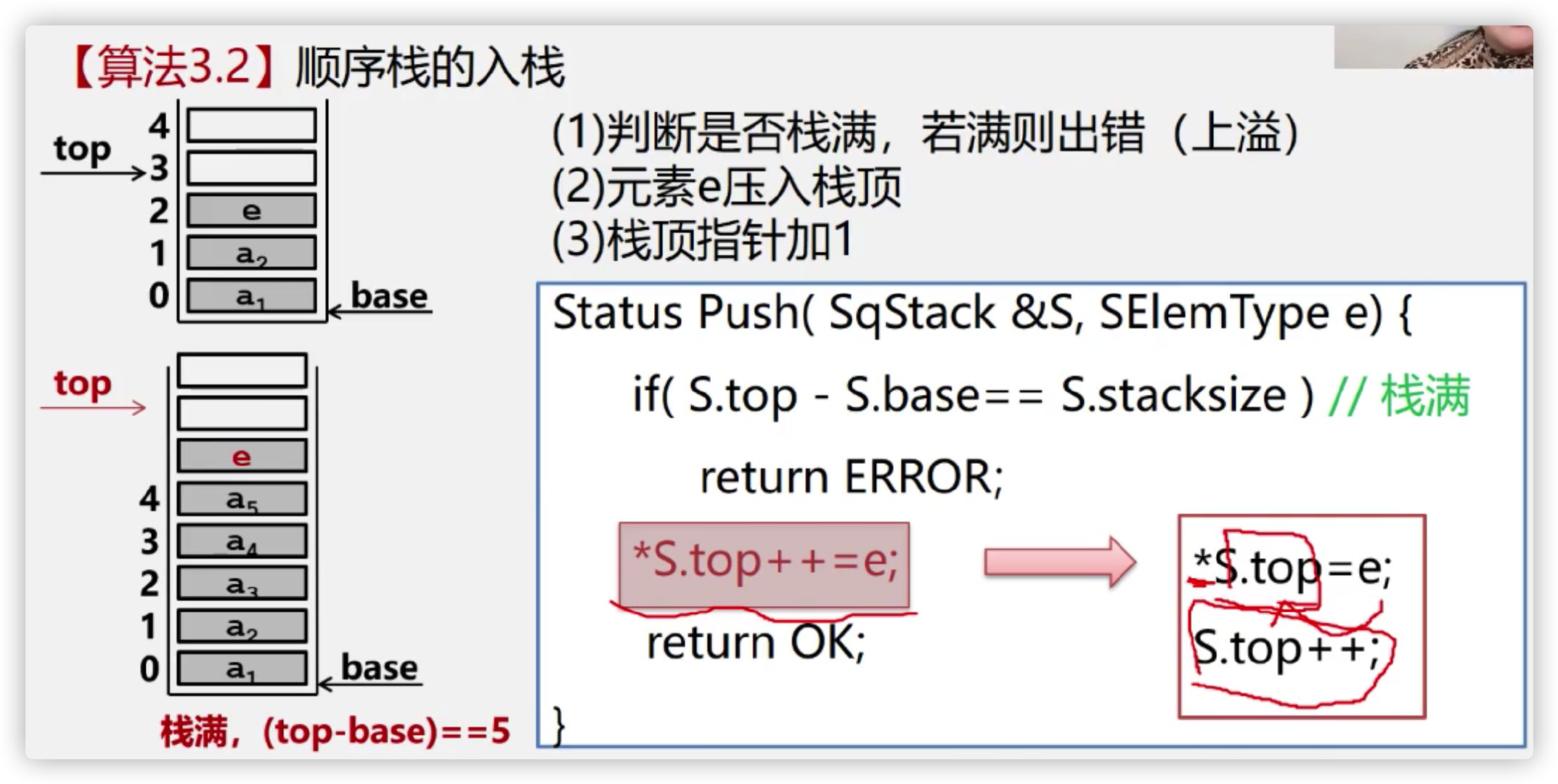
Sequential stack

2. Implementation of chain stack

Initialization stack

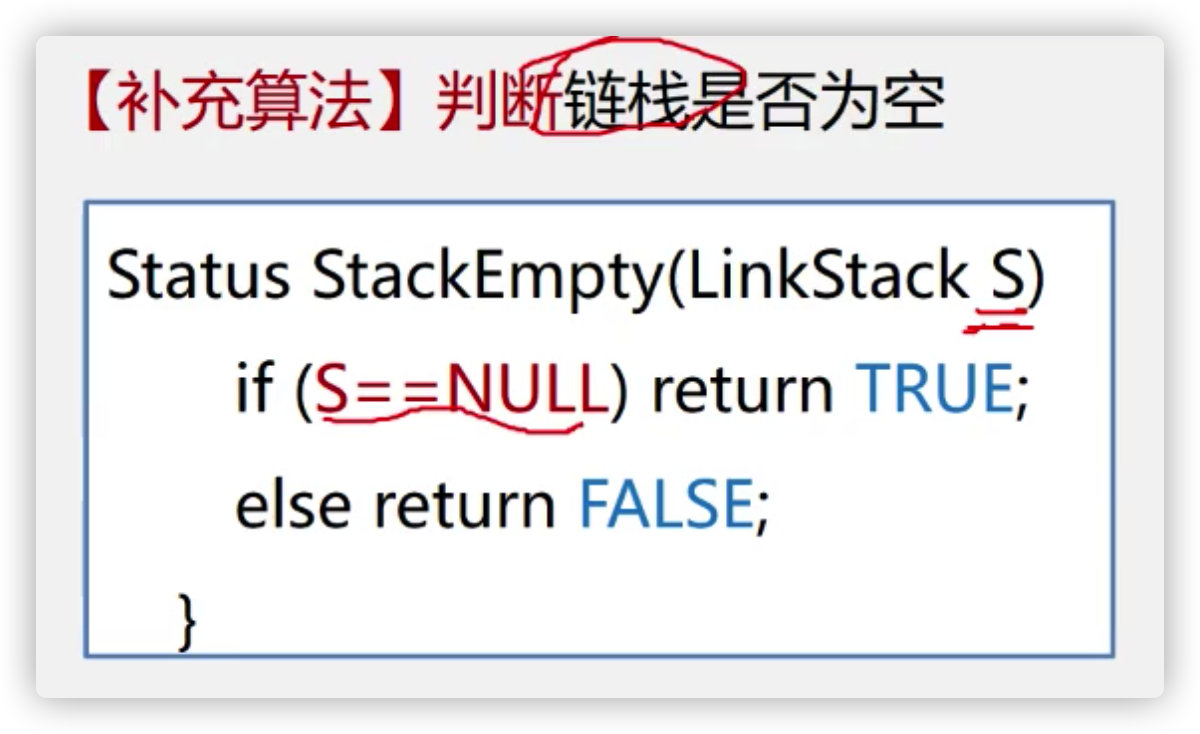
Judge whether the chain stack is empty

Insertion of chain stack

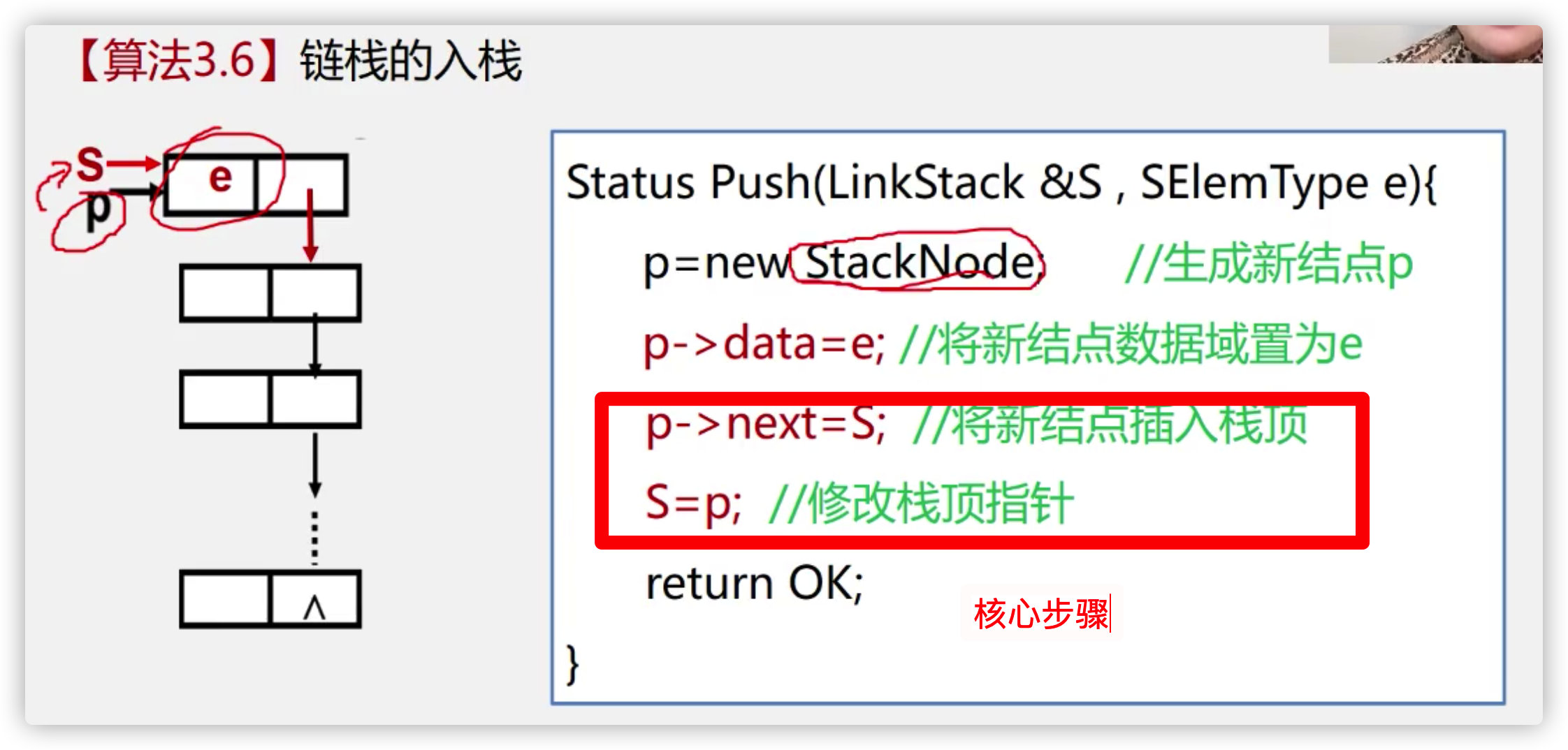
1,initStack(); Initialize stack: make pTop and pBottom point to a useless header node, which creates an empty stack

void initStack(PSTACK pS){
   pS->pTop = (PNODE)malloc(sizeof(NODE)); //Create a null node (PNODE)malloc(sizeof(NODE))
     if (NULL == pS->pTop)
   {
      printf("Dynamic memory allocation failed");
      exit(-1);
   }else{
      pS->pBottom = pS->pTop; // Make both pTop and pBottom point to it
      pS->pTop->pNext = NULL; // pS->pBottom->pNext = NULL;  And set its value to null
   }
}

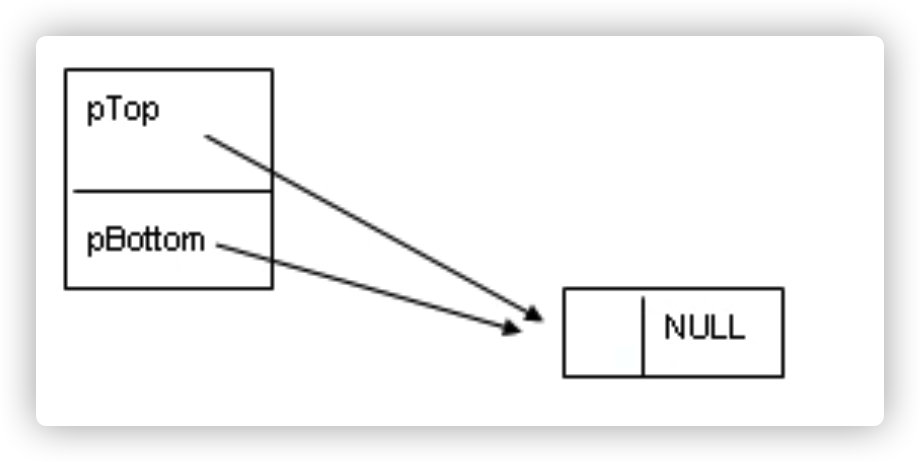
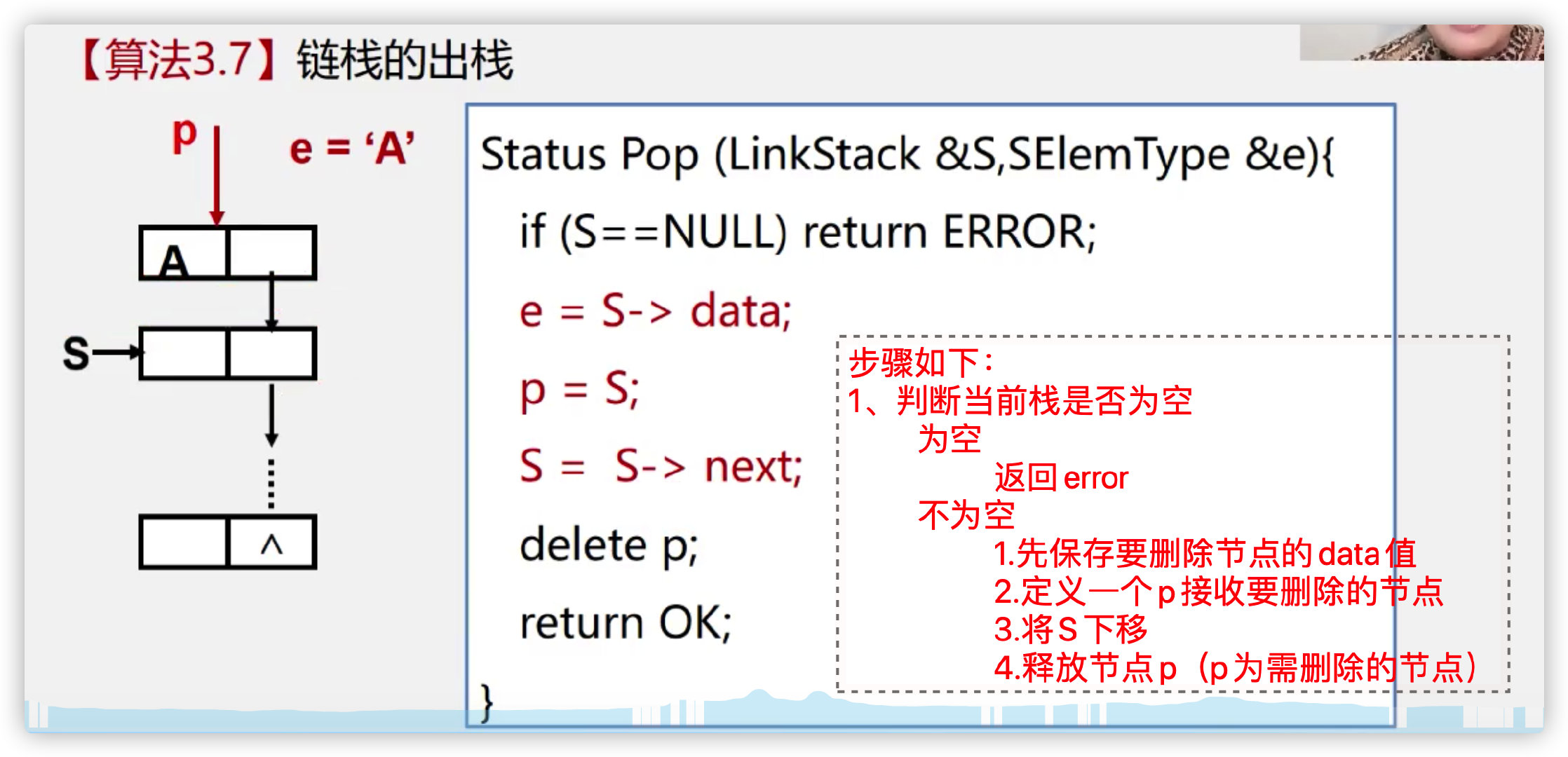
2. Out of stack

// Take the stack pointed to by pS out of the stack once, and store the out of stack element in the variable pointed to by the formal parameter pVal. If the out of the stack fails, return false, otherwise return true;
bool popStack(PSTACK pS,int *pVal){
   if (empt(pS))
   {
      return false;
   }else{
      // Stack out = = = (delete and save the value of the deleted node to the variable pointed to by the formal parameter pVal)
      PNODE r = pS->pTop;
      *pVal = r->data;
      pS->pTop = r->pNext;
      free(r);
      r = NULL;
      return true;
   }
} 

3. Stack pressing

pushStack() implementation

void pushStack(PSTACK pS,int val){
   PNODE pNew = (PNODE)malloc(sizeof(NODE));
   pNew->data = val; 
   pNew->pNext = pS->pTop; //PS - > top cannot be changed to PS - > bottom
   pS->pTop = pNew;
   return;
}

4. traverse traversal

void traverse(PSTACK pS){
   PNODE p = pS->pTop;
   while (p!=pS->pBottom)
   {
      printf("%d ",p->data);
      p = p->pNext;
   }
   printf("\n");
   return;
}

5. Clear

//Empty stack
void clear(PSTACK pS){

   if (empt(pS))
   {
      return ;
   }else{
      PNODE p = pS->pTop;
      PNODE q = NULL;
      while (p != pS->pBottom)
      {
         q = p->pNext;
         free(p);
         p = q;
      }
      pS->pTop = pS->pBottom; // Results after emptying
   }
}

Complete code and implementation of custom stack

#include<stdio.h>
#include<mm_malloc.h>

/**
 Stack implementation
 */

typedef struct Node{
   int data;
   struct Node *pNext;
}NODE,*PNODE; 


typedef struct Stack{
   PNODE pTop; //Top
   PNODE pBottom; // Top
}STACK,*PSTACK;


void initStack(PSTACK); // Initialization stack
void pushStack(PSTACK,int); // Stack pressing
void traverse(PSTACK); // Traversal output
bool popStack(PSTACK,int *);// Out of stack
bool empt(PSTACK); // Is it empty
void clear(PSTACK); //empty

int main(){

   STACK S; // Equivalent to struct Stack S;
   initStack(&S); // Initialization stack: creates an empty stack
   pushStack(&S,1); // Stack pressing
   pushStack(&S,2);
   pushStack(&S,3); // Stack pressing
   pushStack(&S,4);
   pushStack(&S,5); // Stack pressing
   pushStack(&S,6);   
   traverse(&S); // Traversal output
   /*
   printf("\n---------------------\n");
   int val;
   if (popStack(&S,&val))
   {
      printf("Successfully stack. The stack elements are:% d\n",val);
   }else
   {
       printf("Stack out failed! \ n "");
   }

   */
   //Test empty function
   clear(&S);
   traverse(&S); // Traversal output

   return 0; 
}

void initStack(PSTACK pS){
   pS->pTop = (PNODE)malloc(sizeof(NODE));
   if (NULL == pS->pTop)
   {
      printf("Dynamic memory allocation failed");
      exit(-1);
   }else{
      pS->pBottom = pS->pTop;
      pS->pTop->pNext = NULL; // pS->pBottom->pNext = NULL;
   }
   
}

void pushStack(PSTACK pS,int val){
   PNODE pNew = (PNODE)malloc(sizeof(NODE));
   pNew->data = val; 
   pNew->pNext = pS->pTop; //PS - > top cannot be changed to PS - > bottom
   pS->pTop = pNew;
   return;
}

void traverse(PSTACK pS){
   PNODE p = pS->pTop;
   while (p!=pS->pBottom)
   {
      printf("%d ",p->data);
      p = p->pNext;
   }
   printf("\n");
   return;
}

bool empt(PSTACK pS){
   if (pS->pBottom == pS->pTop)
   {
      return true;
   }else{
      return false;
   }
   
}
// Take the stack pointed to by pS out of the stack once, and store the out of stack element in the variable pointed to by the formal parameter pVal. If the out of the stack fails, return false, otherwise return true;
bool popStack(PSTACK pS,int *pVal){
   if (empt(pS))
   {
      return false;
   }else{
      // Stack out = = = (delete and save the value of the deleted node to the variable pointed to by the formal parameter pVal)
      PNODE r = pS->pTop;
      *pVal = r->data;
      pS->pTop = r->pNext;
      free(r);
      r = NULL;
      return true;
   }
} 

//Empty stack
void clear(PSTACK pS){

   if (empt(pS))
   {
      return ;
   }else{
      PNODE p = pS->pTop;
      PNODE q = NULL;
      while (p != pS->pBottom)
      {
         q = p->pNext;
         free(p);
         p = q;
      }
      pS->pTop = pS->pBottom; // Results after emptying
   }
}

(3) Application binary conversion

thinking

(4) Application - Verification of expression bracket matching

Stack rule: the parentheses that are put on the stack first and then matched, and the parentheses that are put on the stack later are matched first

(5) Application - expression evaluation

4. Queue

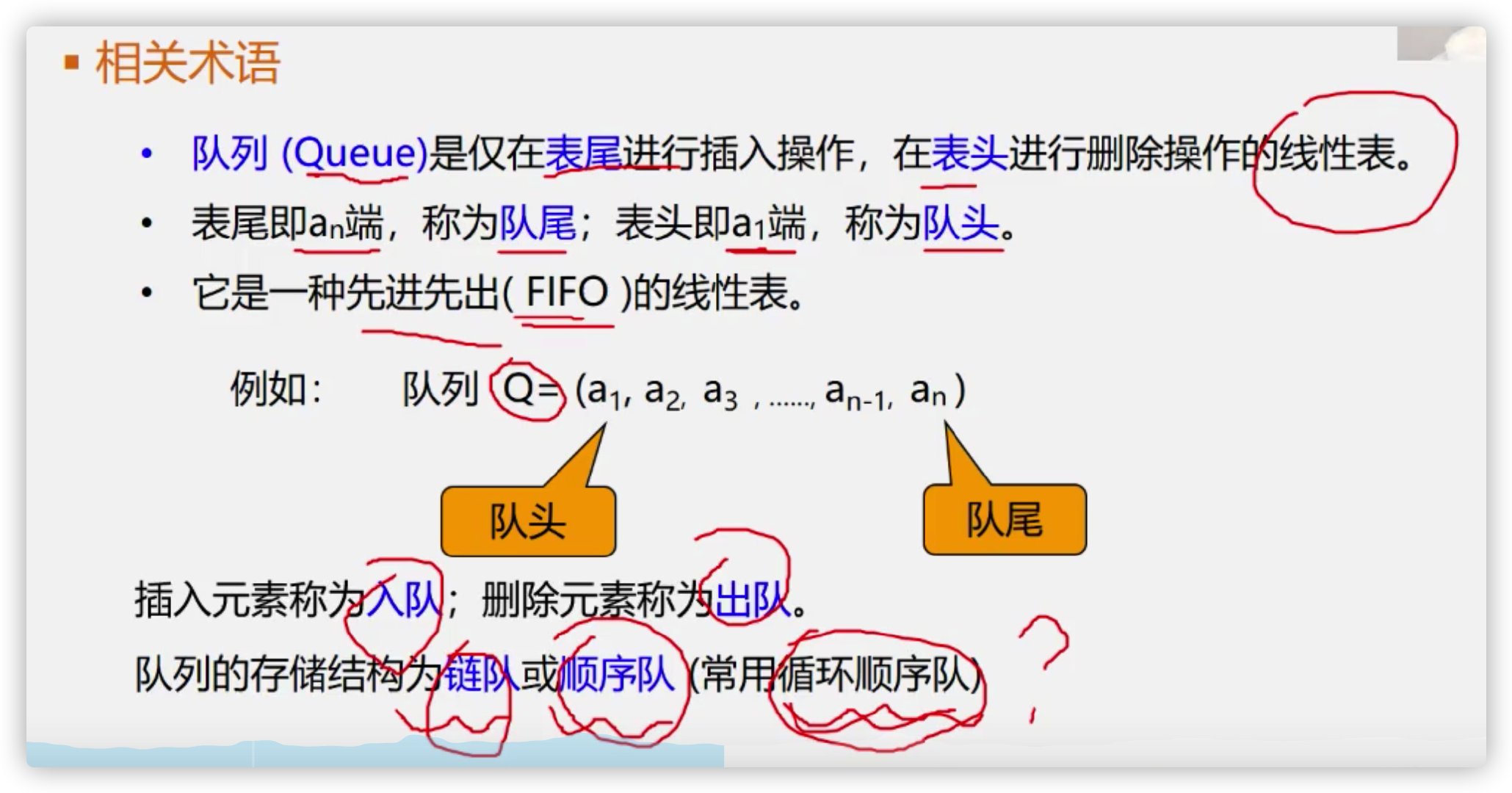
(1) Definition:

It is a storage structure that can realize "first in, first out"! Similar to: queue up to buy tickets

(2) Related terms

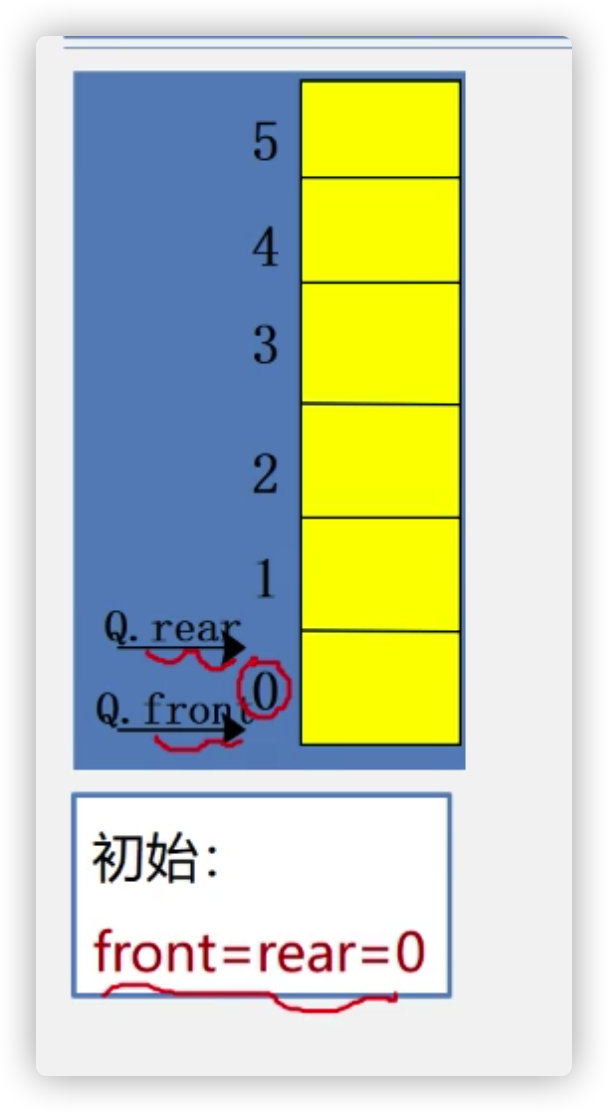
(3) Implementation of sequential queue

During initialization:

There are elements in the team:

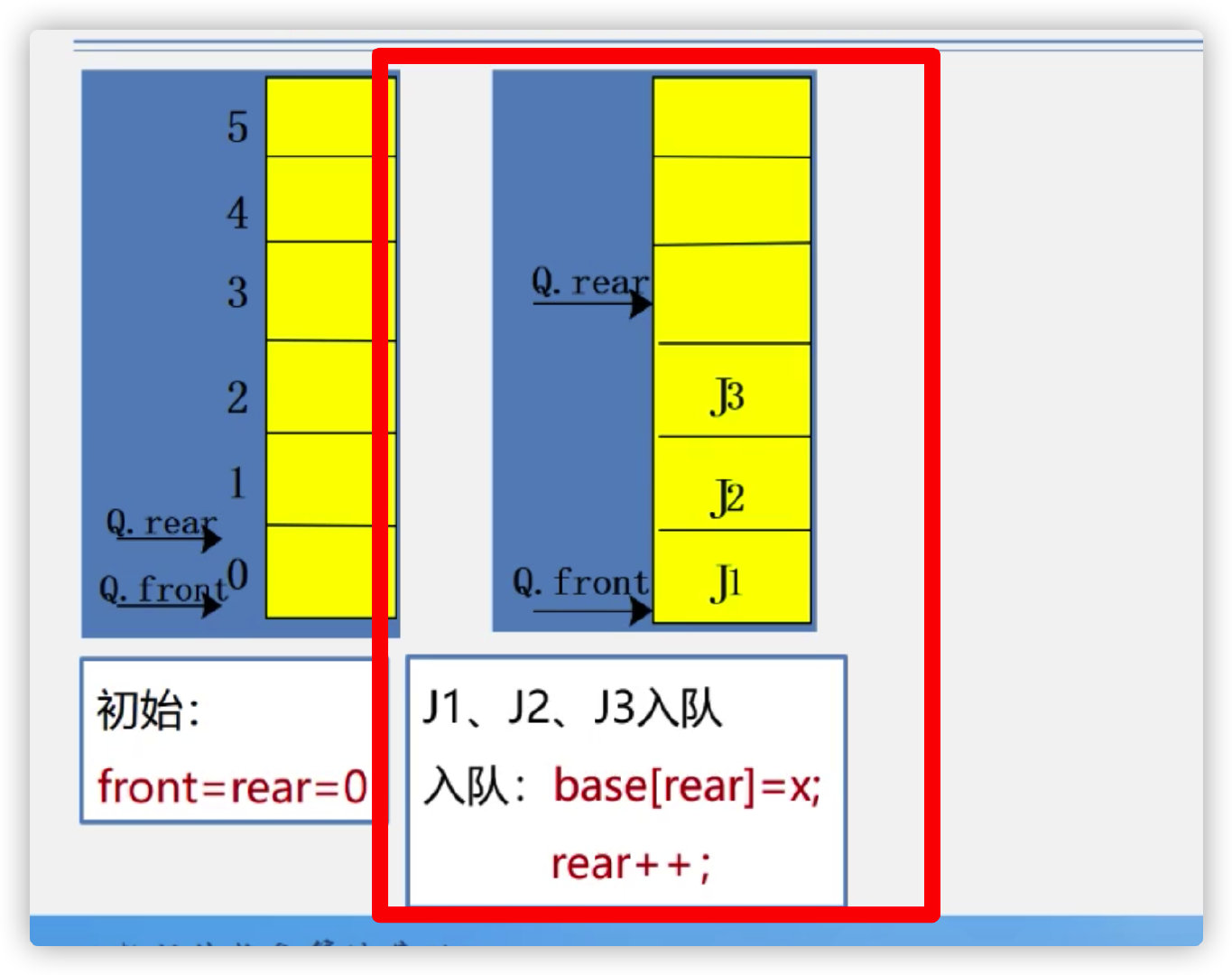
Some elements are out of the team:

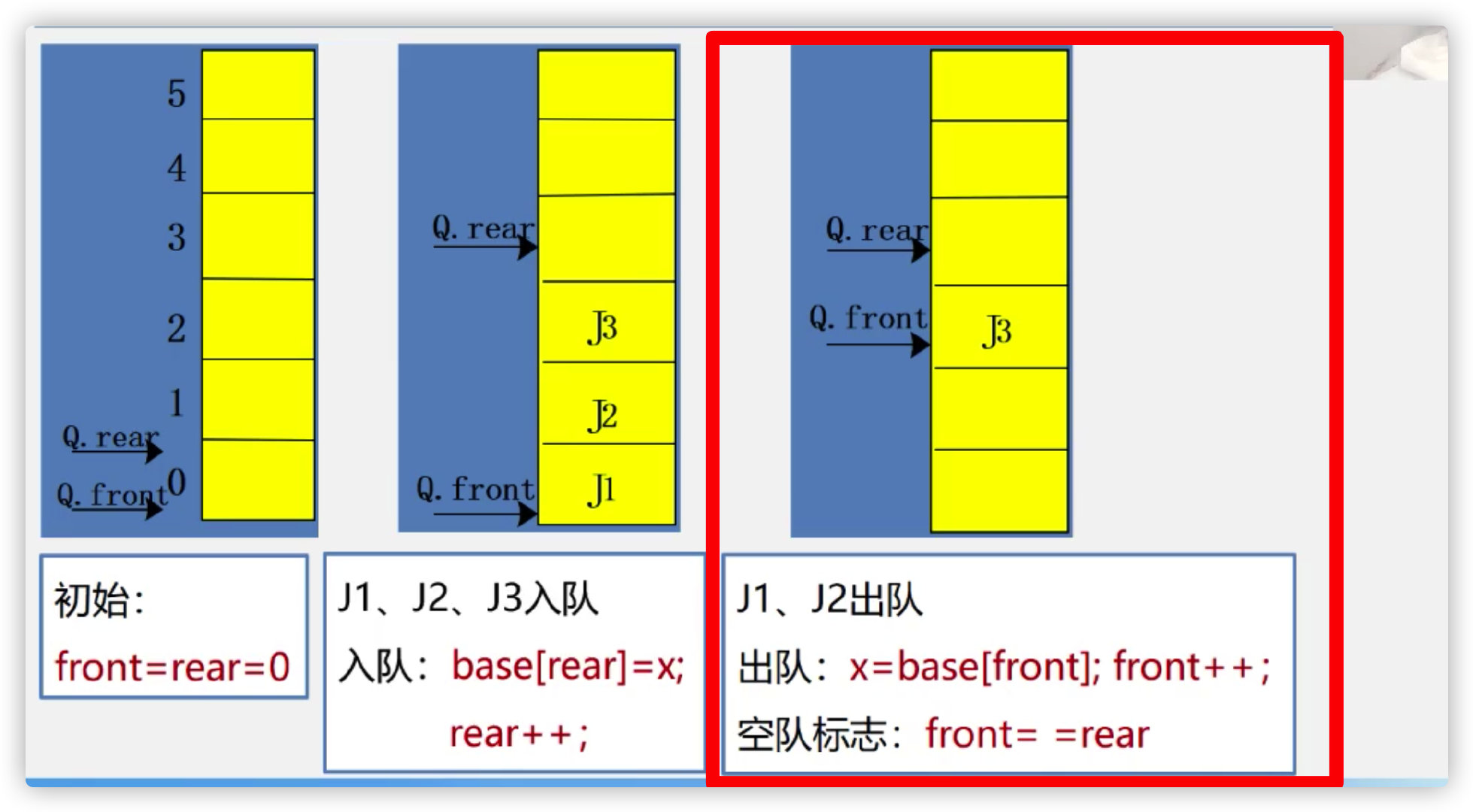
Introduce circular queue

Solve the problem of false overflow during insertion

Solve the problem of false overflow during deletion

Similar to the effect of implementing circular queues

How to judge whether the team is empty or full

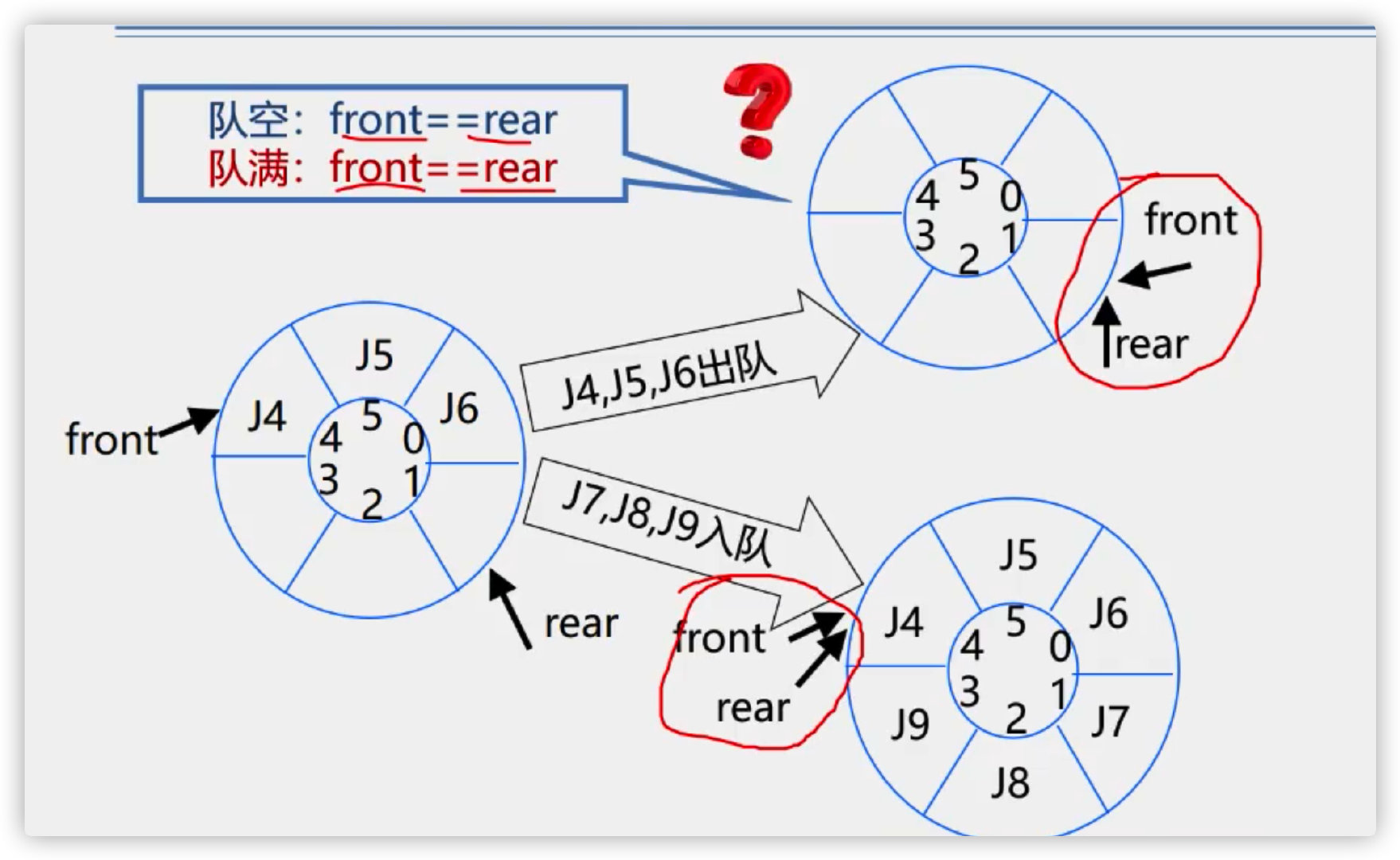
Method 1: set another flag to judge whether the team is empty or full

Method 2: set another count to count the number

Method 3: use less one element space

The third method is as follows:

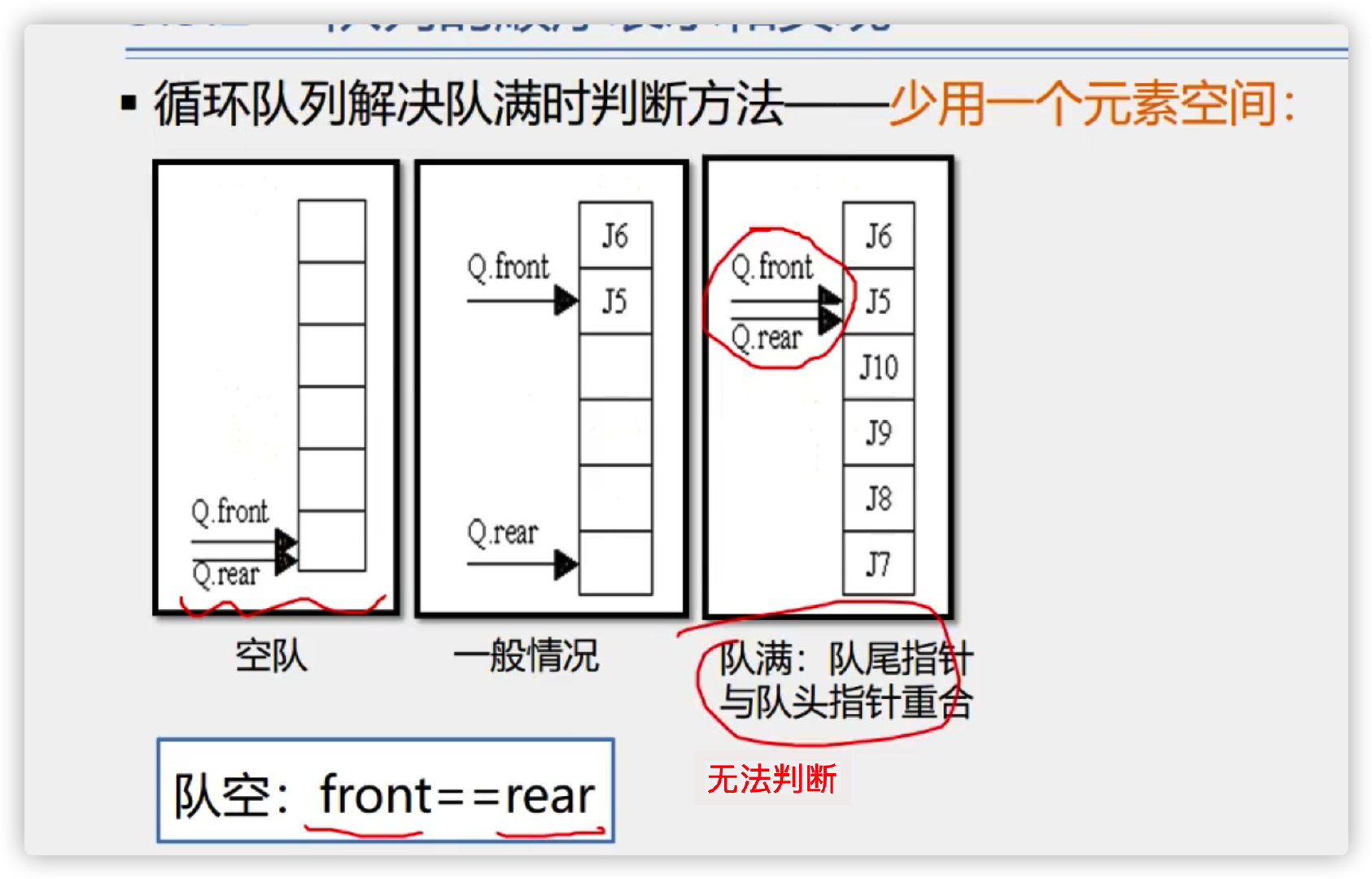
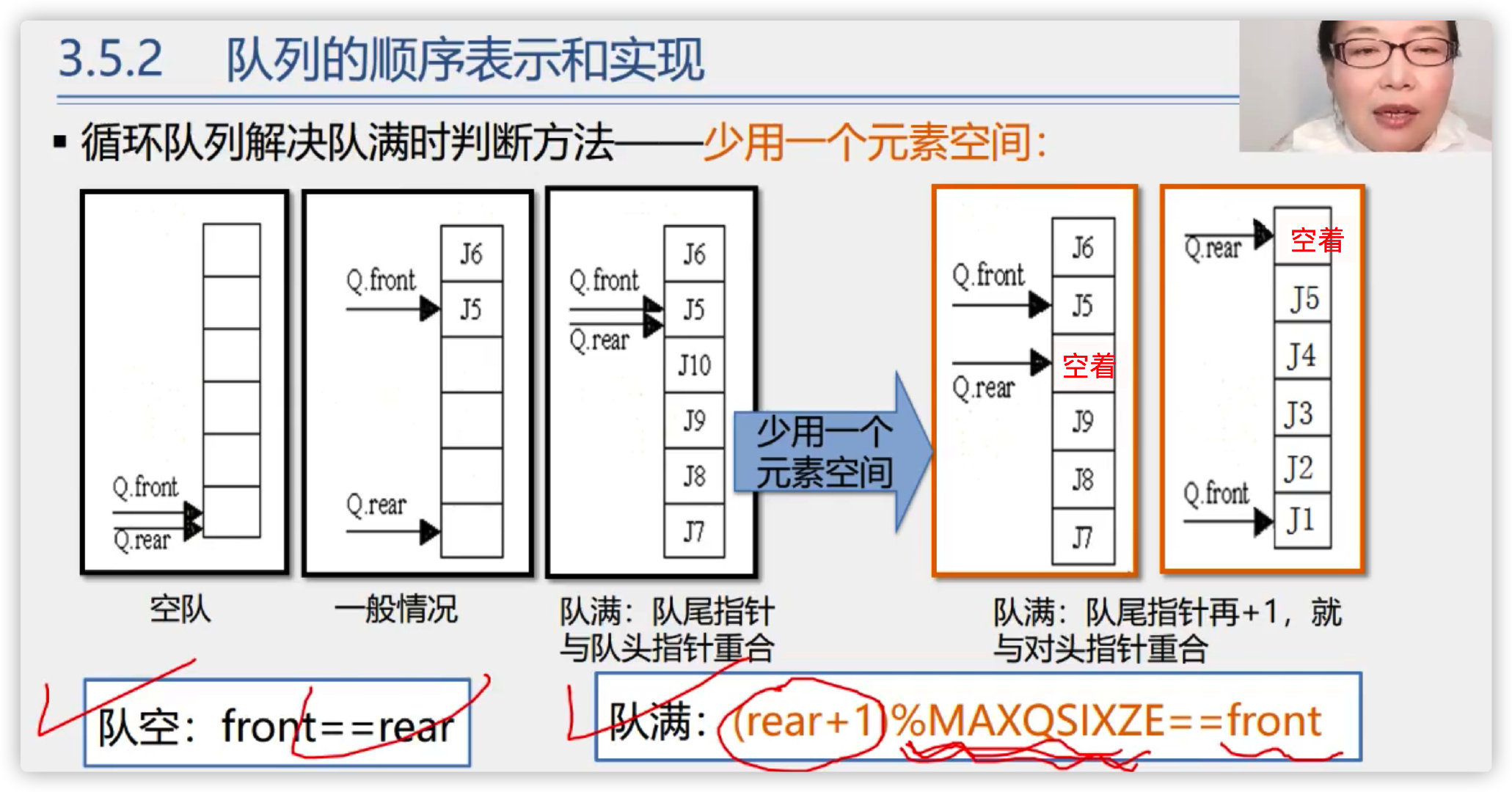
Code implementation:

0. Structure

1. Initialization operation

2. Find the length of the queue

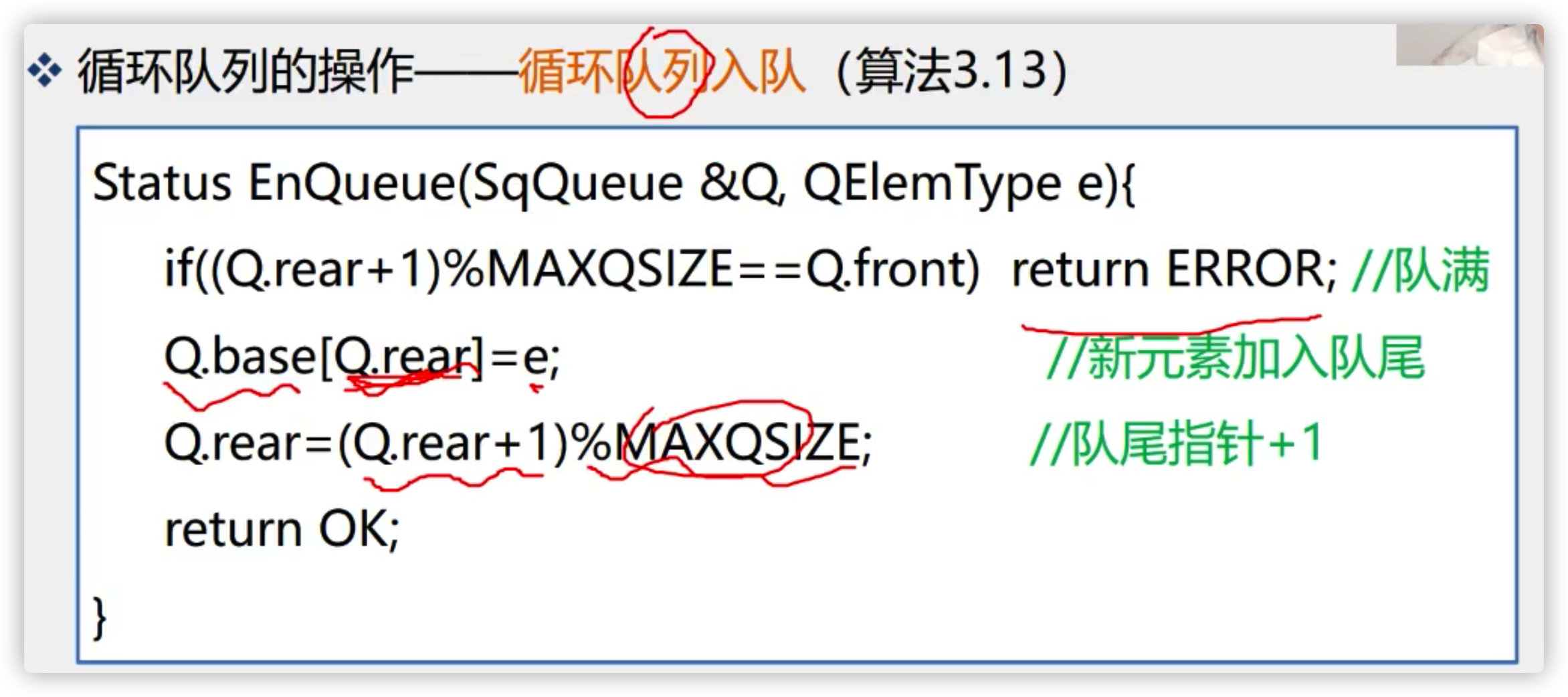
3. Queue entry algorithm for circular queue

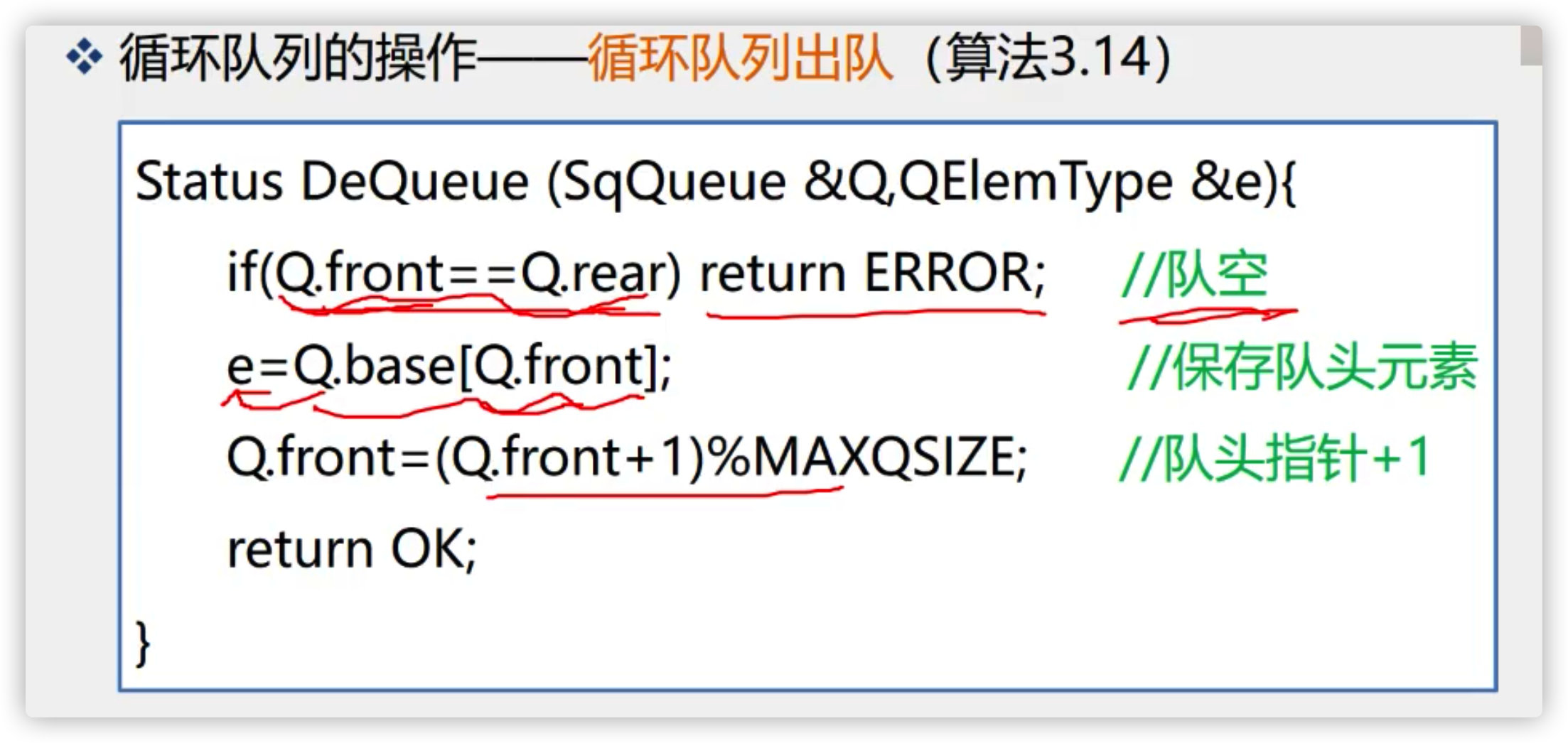
4. Out of queue algorithm for cyclic queue

a,First judge whether it is empty. If it is empty, you cannot exit the queue

b,Keep deleted elements

c,Header pointer+1

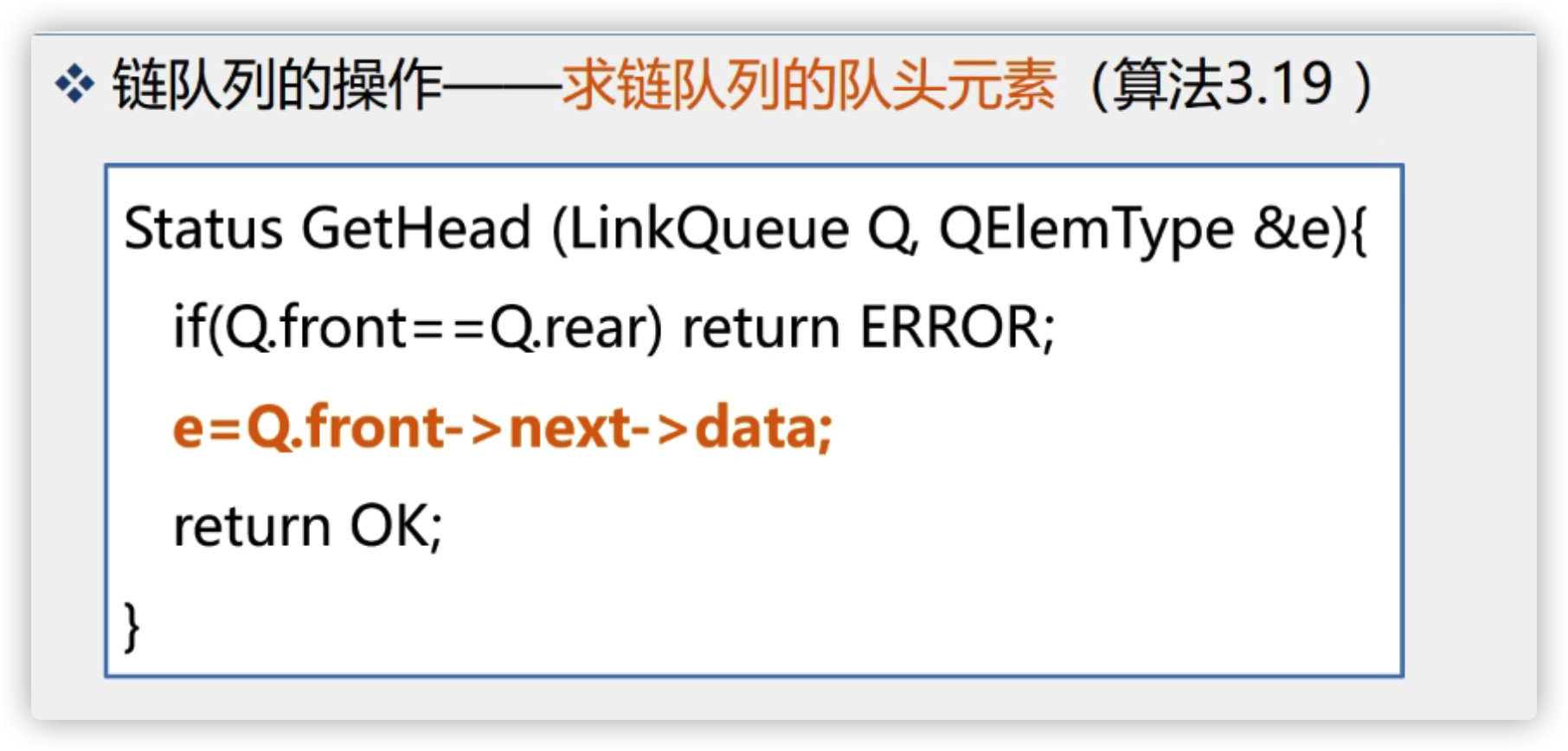
5. Take out the header element

a,Premise: the queue cannot be empty
b,Direct extraction front Value of location

(4) Implementation of chain queue

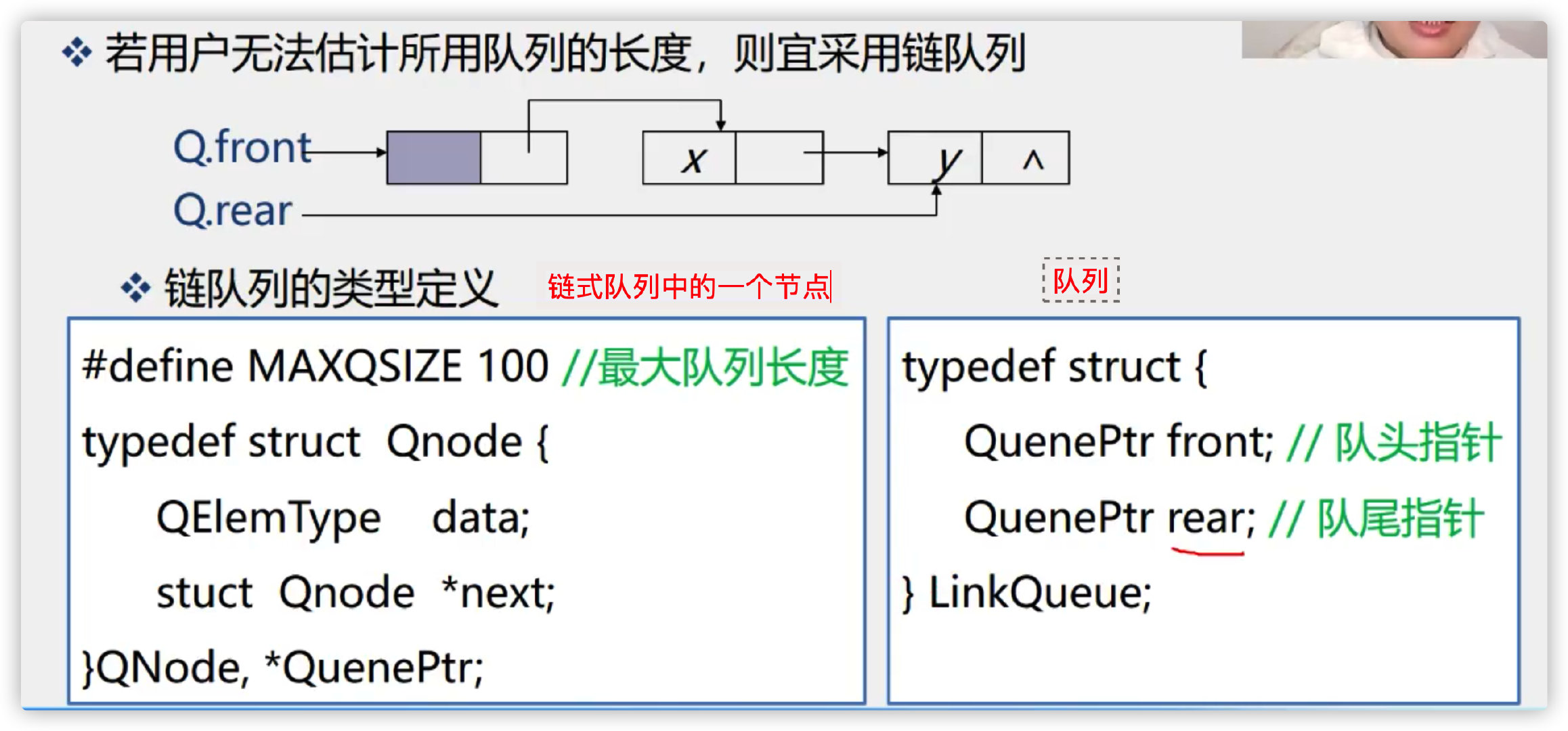
1. Initialization of chained queues

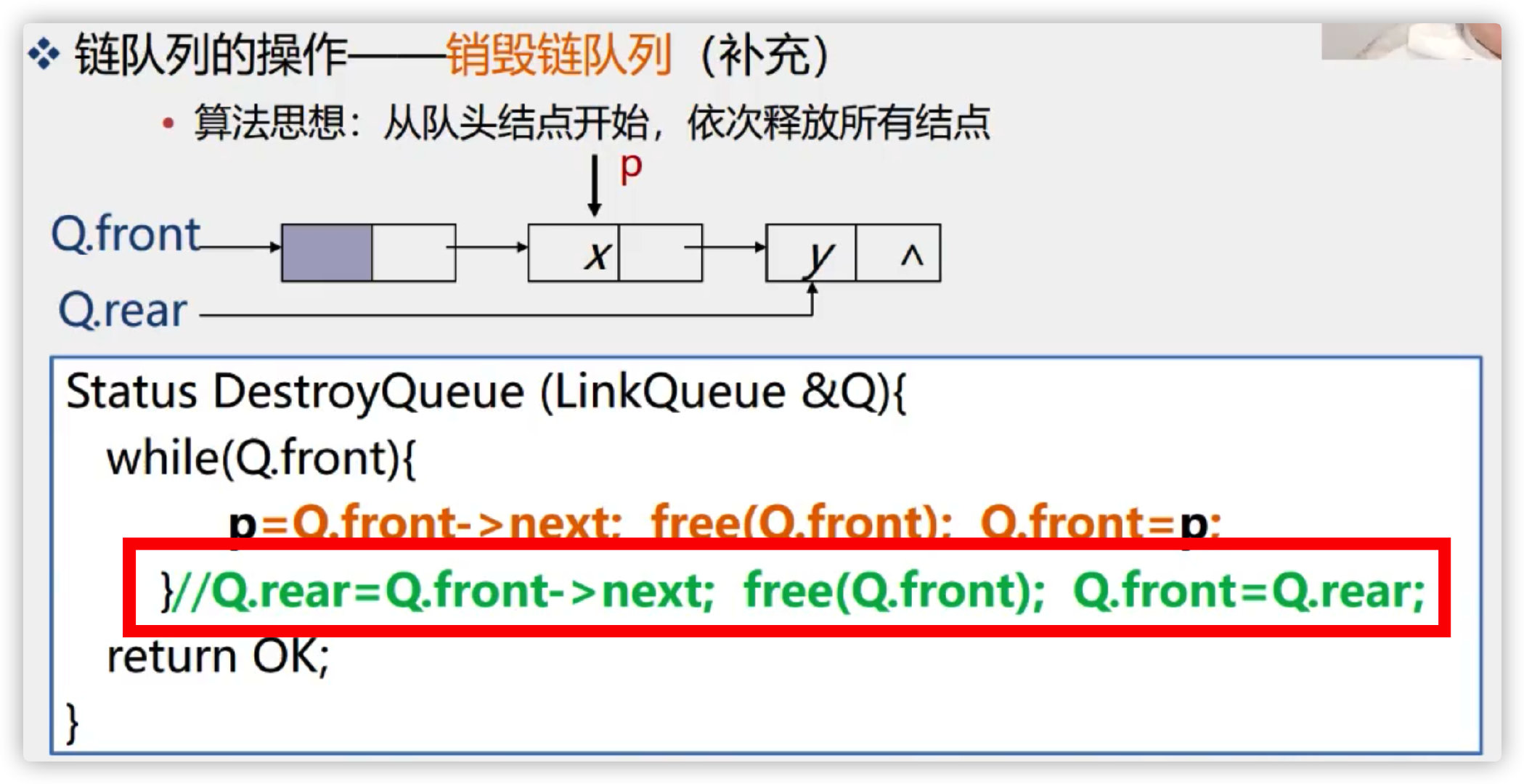
2. Destruction of chained queues

Method 1: define another pointer variable p for receiving

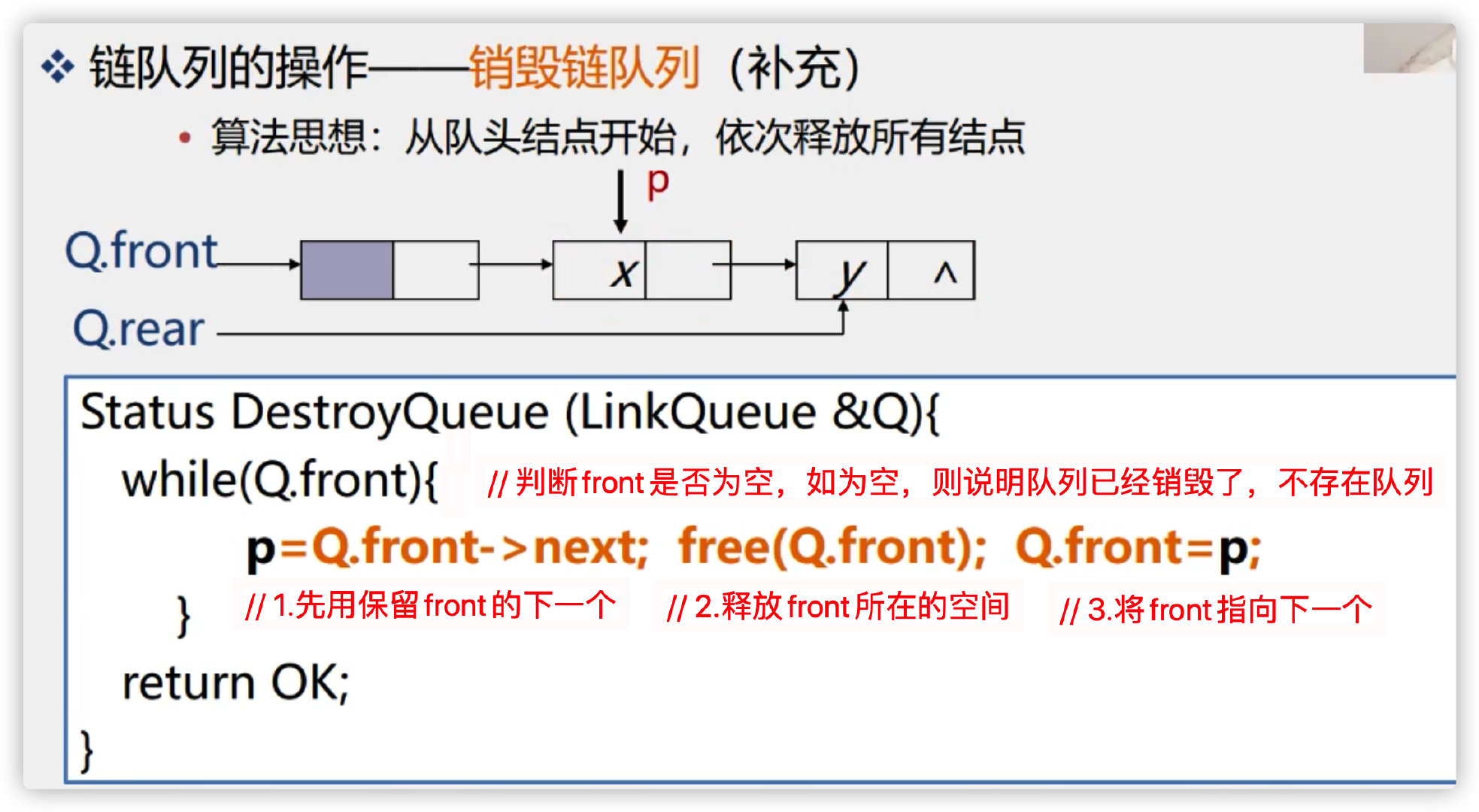
Mode 2: directly receive with Q.rear to save space

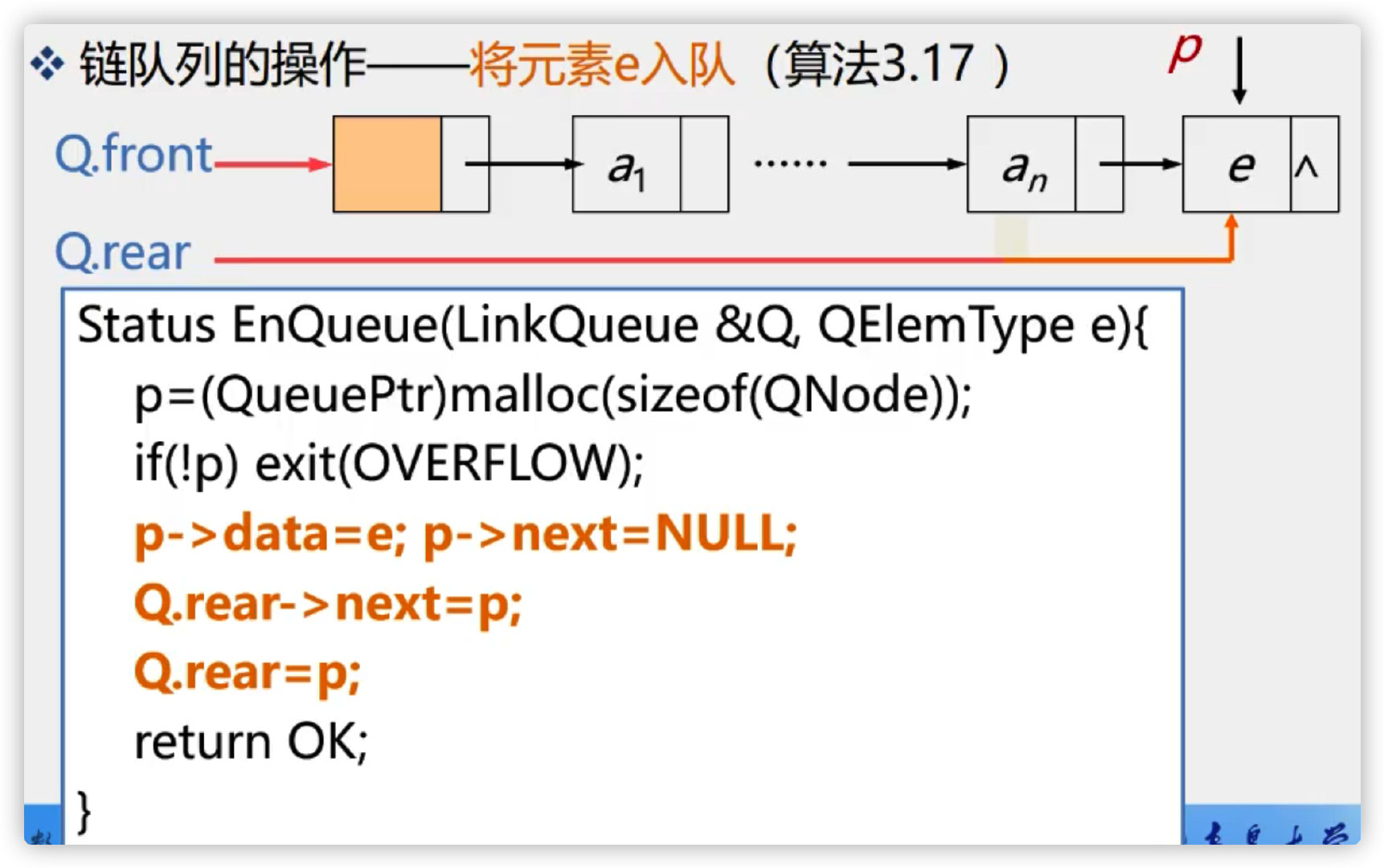
3. Queue up of chain queue

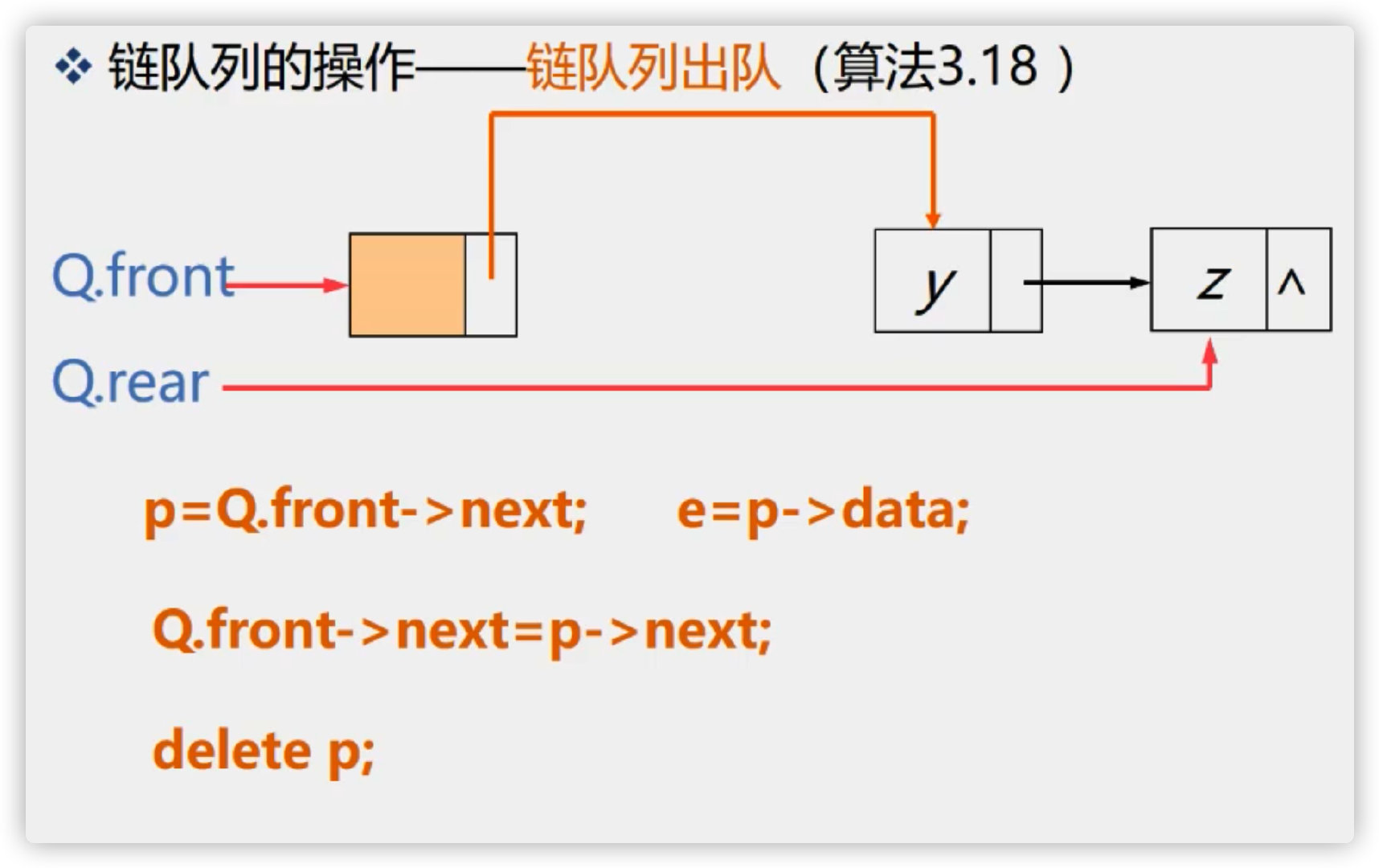
4. Outgoing of chain queue

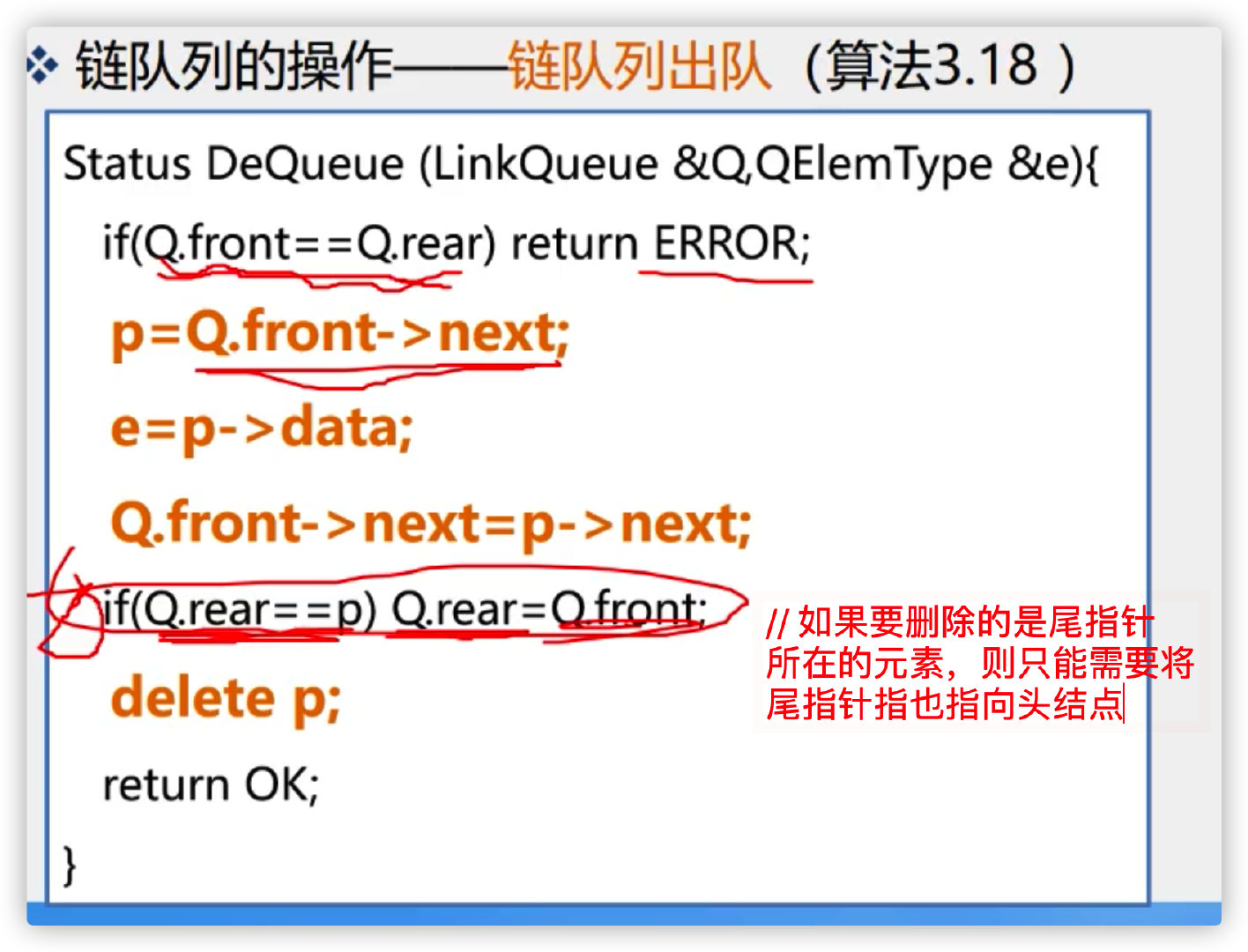
5. Gets the queue element of the chain queue

Static queues must be circular queues

analysis:

1. Why must a static queue be a circular queue?

Because static queues are implemented based on arrays, if circular queues are not used, the space used by deleted elements will not continue to be used, resulting in a waste of space

2. The circular queue requires several parameters to determine

A: two parameters are needed to determine. These two parameters have different meanings on different occasions (remember them first, and then experience them slowly)

front

rear

3. Meaning of parameters of circular queue

These two parameters have different meanings on different occasions (remember them first, and then experience them slowly)

a. initialization: the values of front and rear are both zero

b. the queue is not empty: front represents the first element of the queue, and rear represents the next element of the last valid element of the queue

c. empty queue: the values of front and rear are equal but not necessarily zero

4. Explanation of pseudo algorithm of circular queue inclusion

Two steps:

(1) Store the value in the position represented by r

(2) . wrong writing: rear=rear+1

Correct writing: rear=(rear + 1)% length of array

5. Explanation of pseudo algorithm for out of queue of circular queue

(1) . save the outgoing value first

(2) , front = (front+1)% array length

6. How to determine whether the circular queue is empty

If (front == rear), the queue must be empty

7. How to determine whether the circular queue is full

There are two ways

(1) . add one more flag parameter, len- used to record the length

(2) . use one less element. If front and rear are next to each other, the queue is full

if(front ==(rear+1)%Array length){
  already expired
}else{
  Not full
}

Implementation of queue

#include<stdio.h>
#include<mm_malloc.h>
/*
    queue
*/
typedef struct Queue{
    int * pBase;
    int front;
    int rear;
}QUEUE;

// statement
void init(QUEUE *pQ); // initialization
bool en_queue(QUEUE *pQ,int val);  //Join the team
bool out_queue(QUEUE *pQ,int *pVal);  //Dequeued * pVal is used to save the dequeued value 
void traverse_queue(QUEUE *pQ); // ergodic
bool full_queue(QUEUE *pQ); //Judge whether it is full


int main(){
    QUEUE Q; //  Structure variable
    init(&Q);
    en_queue(&Q,1);
    en_queue(&Q,2);
    en_queue(&Q,3);
    en_queue(&Q,4);
    en_queue(&Q,5);
    en_queue(&Q,6);
    en_queue(&Q,7);
    en_queue(&Q,8);
    traverse_queue(&Q);

    return 0;
}



void init(QUEUE *pQ){
    pQ->pBase = (int *)malloc(sizeof(int)*4); // Represents an array
    pQ->front = 0;
    pQ->pBase = 0;
}


bool full_queue(QUEUE *pQ){
    if ((pQ->rear+1) % 6 == pQ->front)
    {
        return true;
    }else
    {
        return false;
    }
}

bool en_queue(QUEUE *pQ,int val){
    if(full_queue(pQ)){
        return false;
    }else
    {
        pQ->pBase[pQ->rear] = val;  // Put val in the rear position
        pQ->rear = (pQ->rear+1) % 6; // Move the rear one position back
        return true;
    }
}

void traverse_queue(QUEUE *pQ){
    // Traverse from the head. As long as you don't point to r, traverse back
    int i = pQ->front;
    printf("1111");
    while (i!= pQ->rear)
    {
        printf("2222");
        printf("%d ",pQ->pBase[i]);
        i = (i+1)%6 ;
    }
    return; 
}

(6) Application - partner problem

5. Recursion

1, Recursive principle analysis

(1) Definition of recursion

(2) Divide and conquer

(3) Function call procedure

(4) Recursion and stack

Analyzing recursion and stack with hierarchical problem

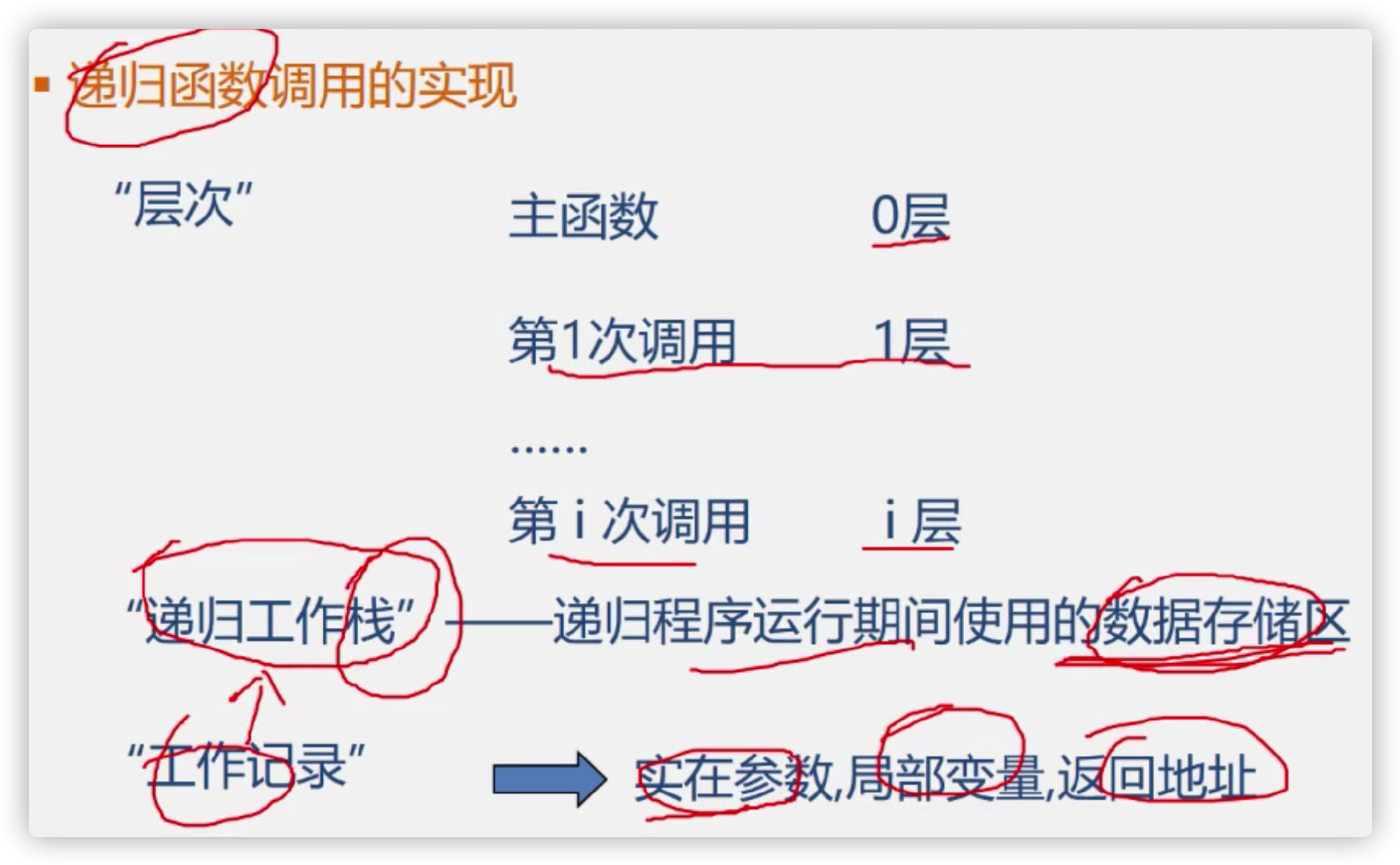
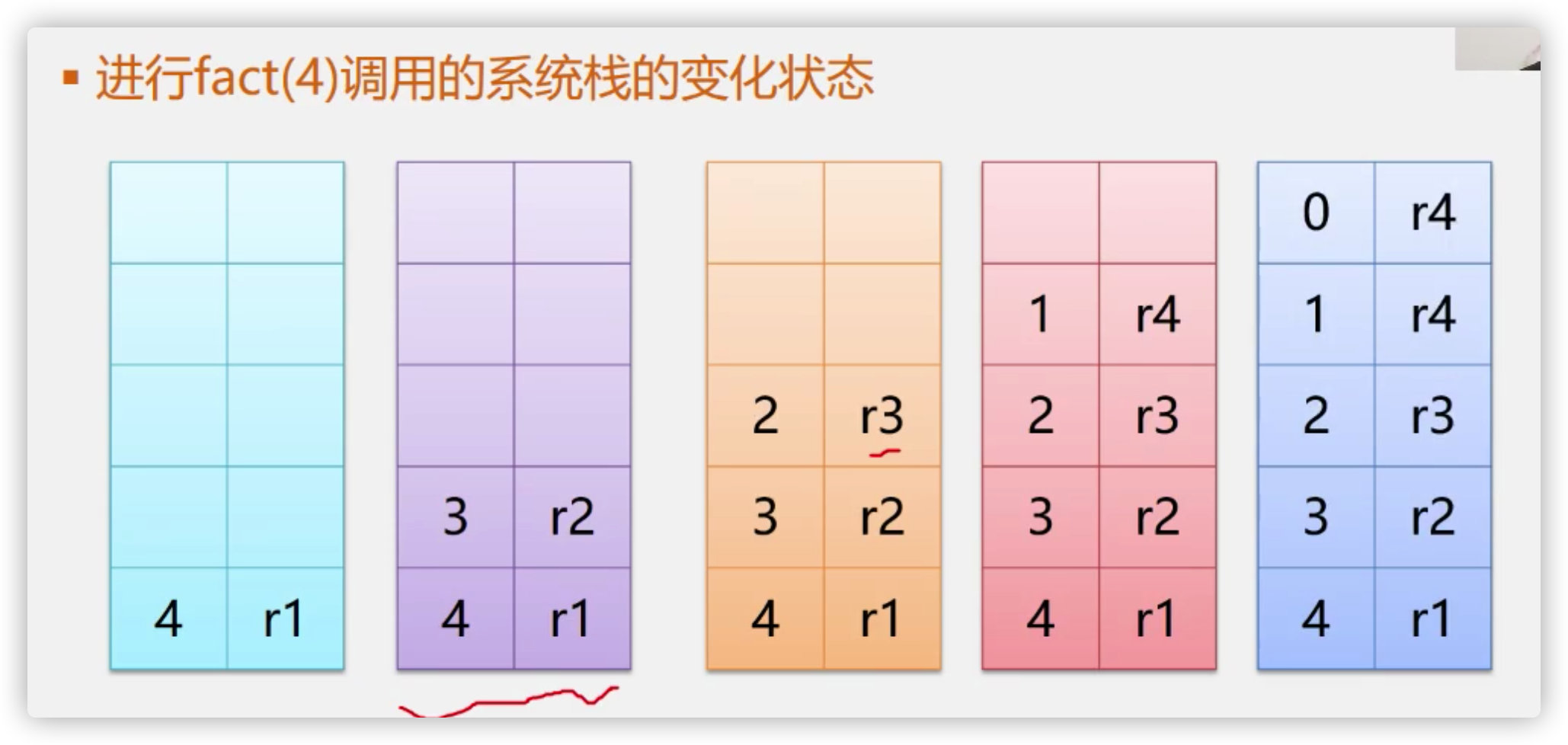
2, Related applications

(1) Seeking stratum

#include<stdio.h>
// Class seeking n
long getJC(long n){
    if(n==1){
        return 1;
    }else
    {
       return getJC(n-1) * n;
    }
    
    
}
int main(){
    printf("result=%ld",getJC(20));
    return 0;
}

(2) Sum of 1 + 2 + 3 +... + 100

#include<stdio.h>
// Find the sum of 1 to 100
long getSum(long n){
    if(n==1){
        return 1;
    }else
    {
       return getSum(n-1) + n;
    }
    
    
}
int main(){
    printf("sum=%ld",getSum(100));
    return 0;
}

(3) Maze

(4) Hanoi Tower

Function call

When another function is called during the operation of one function, the system needs to complete three things before running the backtone function:

1) Send all the actual parameters, return address and other information to the called function

2) Allocate memory space for local variables (including formal parameters) of the called function

3) Move the control switch to the entrance of the called function and allocate space

When returning the calling function from the called function, the system also needs to complete three things:

1) . save the return result of the called function

2) . release the storage space occupied by the called function

3) Transfer the control to the place of the calling function according to the return address saved by the called function

Application of recursion

Numbers and forests are defined recursively

Many algorithms of numbers and graphs are implemented by recursion

Many mathematical formulas are defined recursively

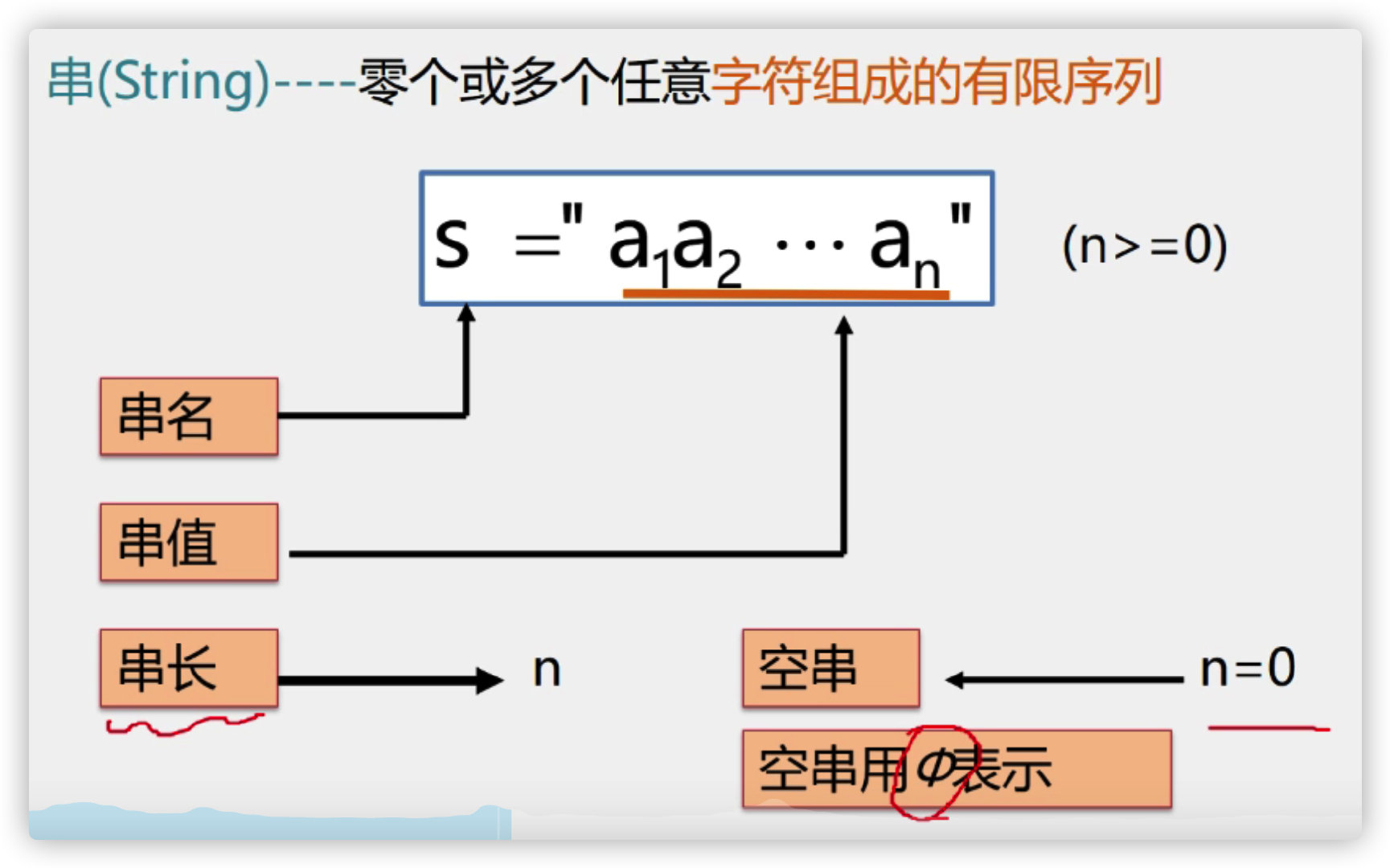
6. String

String - a finite sequence of zero or more arbitrary characters

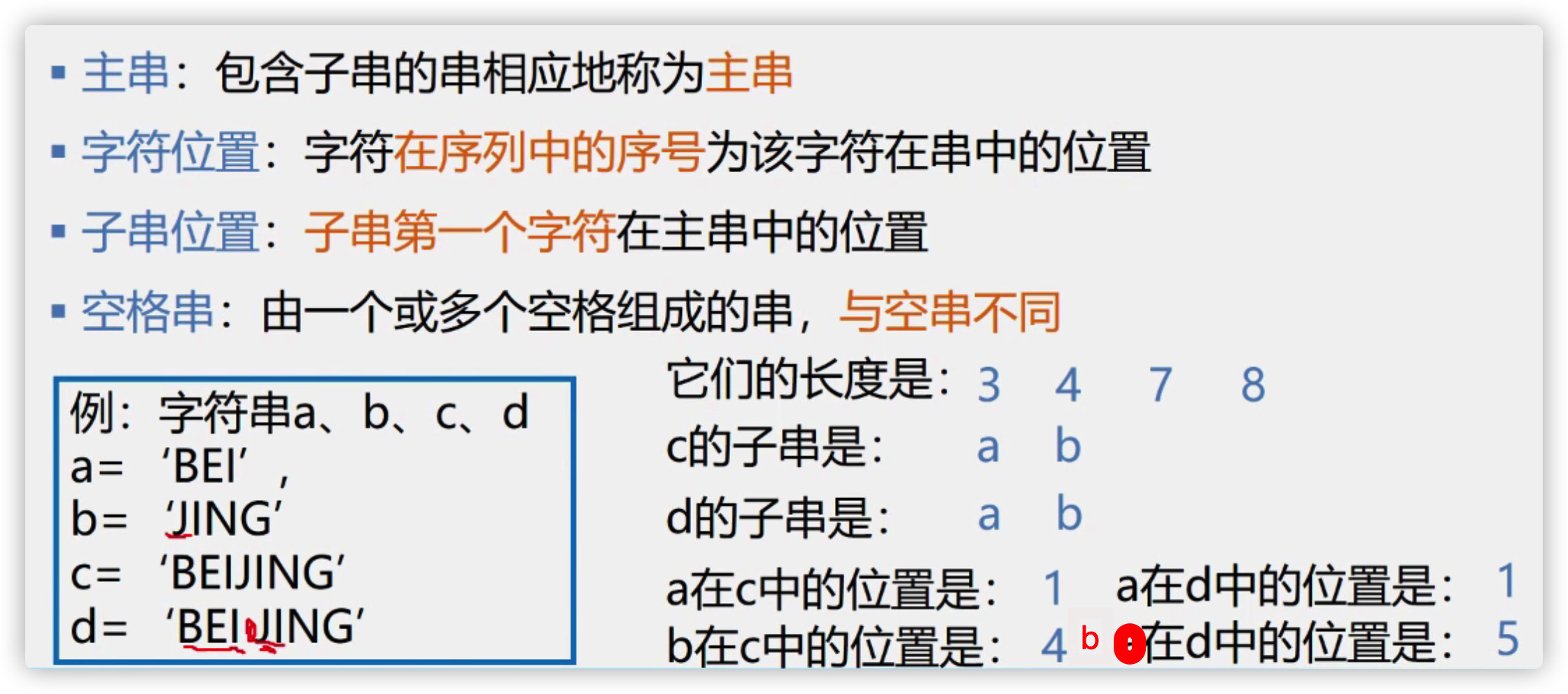
Terms about strings

Substring, true substring, main string, character position, substring position, space string, string equality

Case introduction

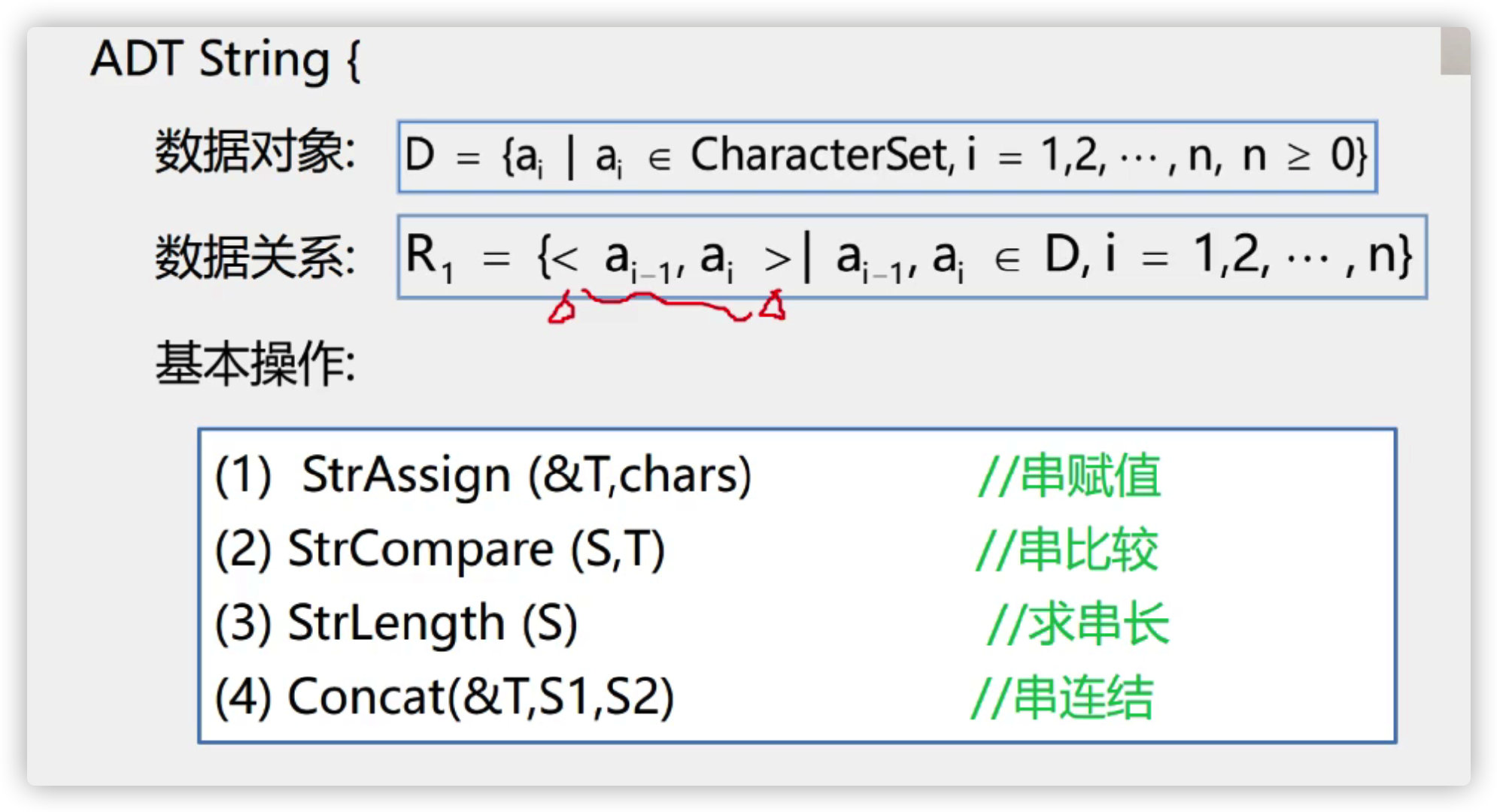
Definition, storage structure, algorithm and operation of string

structural analysis

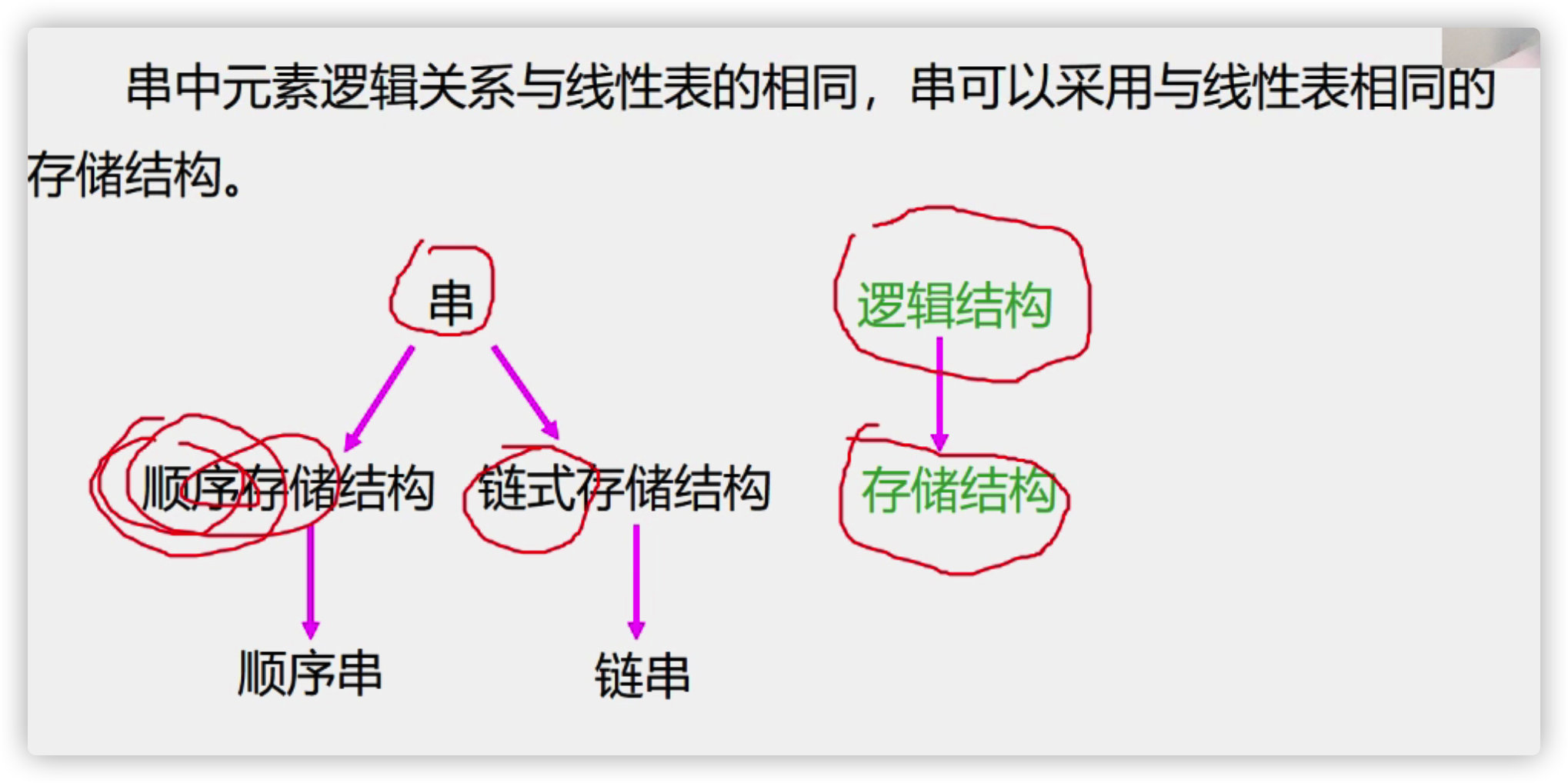
(1) Storage mode of string

1. Sequential storage structure of string

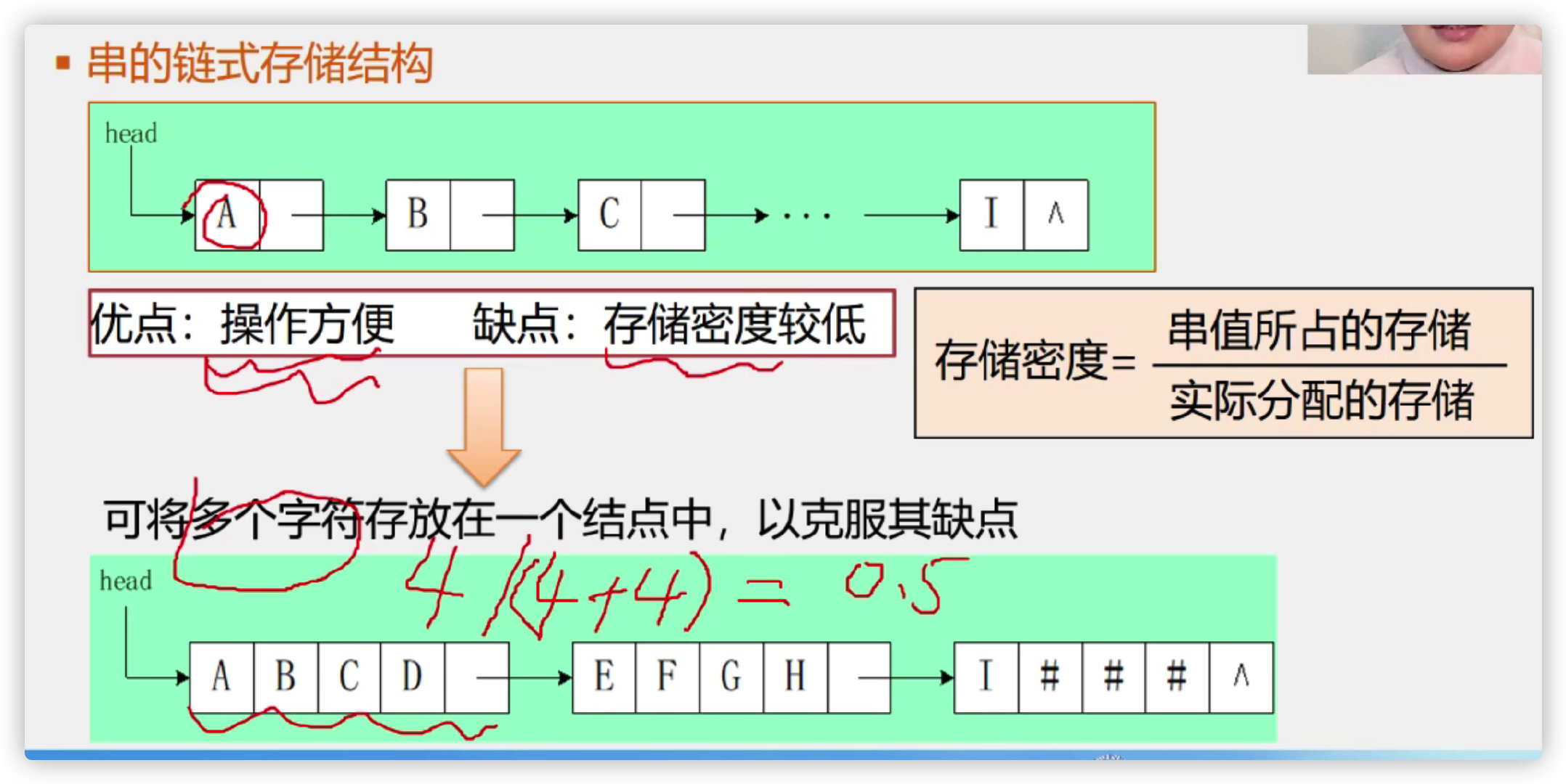
2. Chain storage structure of string

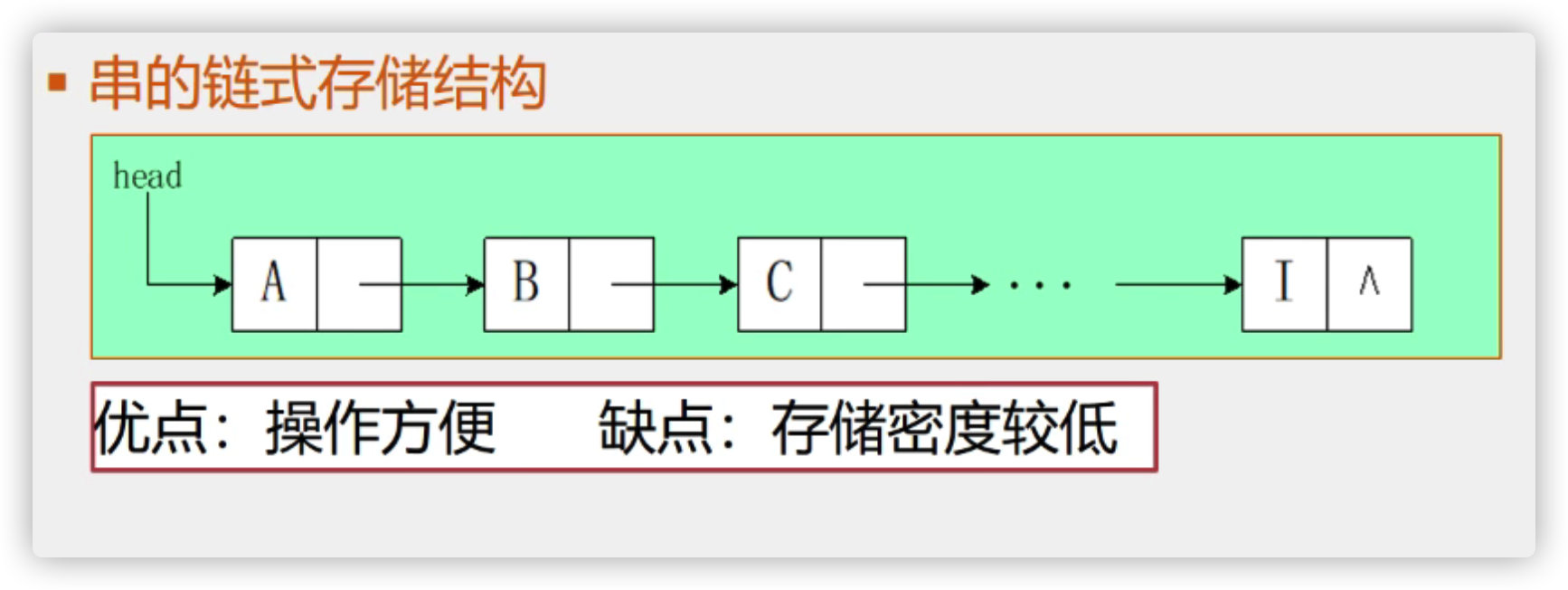
The improved method is to place multiple characters in one node. To overcome its shortcomings

(2) Pattern matching algorithm of string

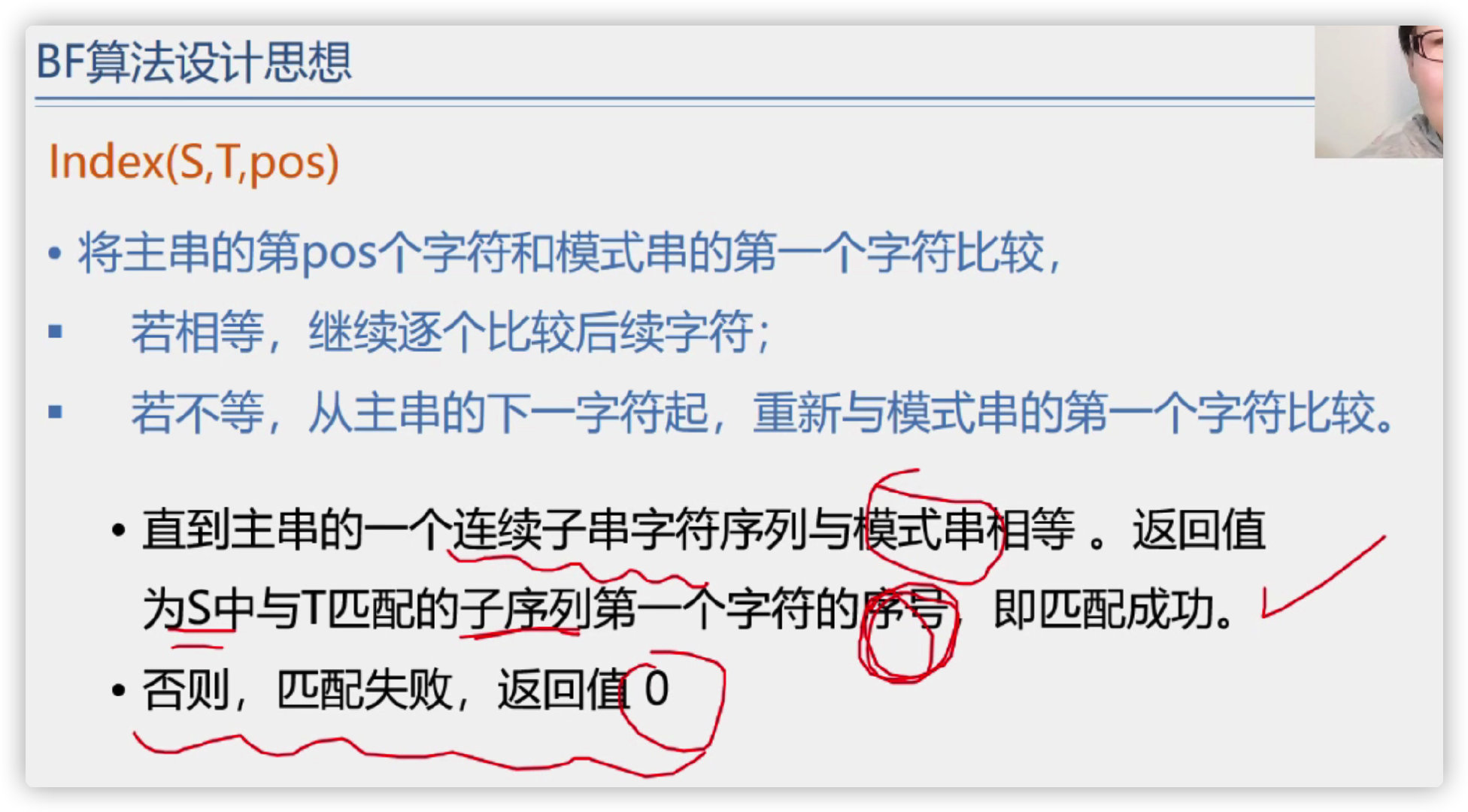
Algorithm purpose: determine the position (location) of * * substring (mode string) * * contained in the main string for the first time

**Algorithm application: * * search engine, spell check, language translation, data compression

Algorithm type:

• BF algorithm (brute force, also known as classical, classical, simple and exhaustive)
• KMP algorithm (feature: high speed)

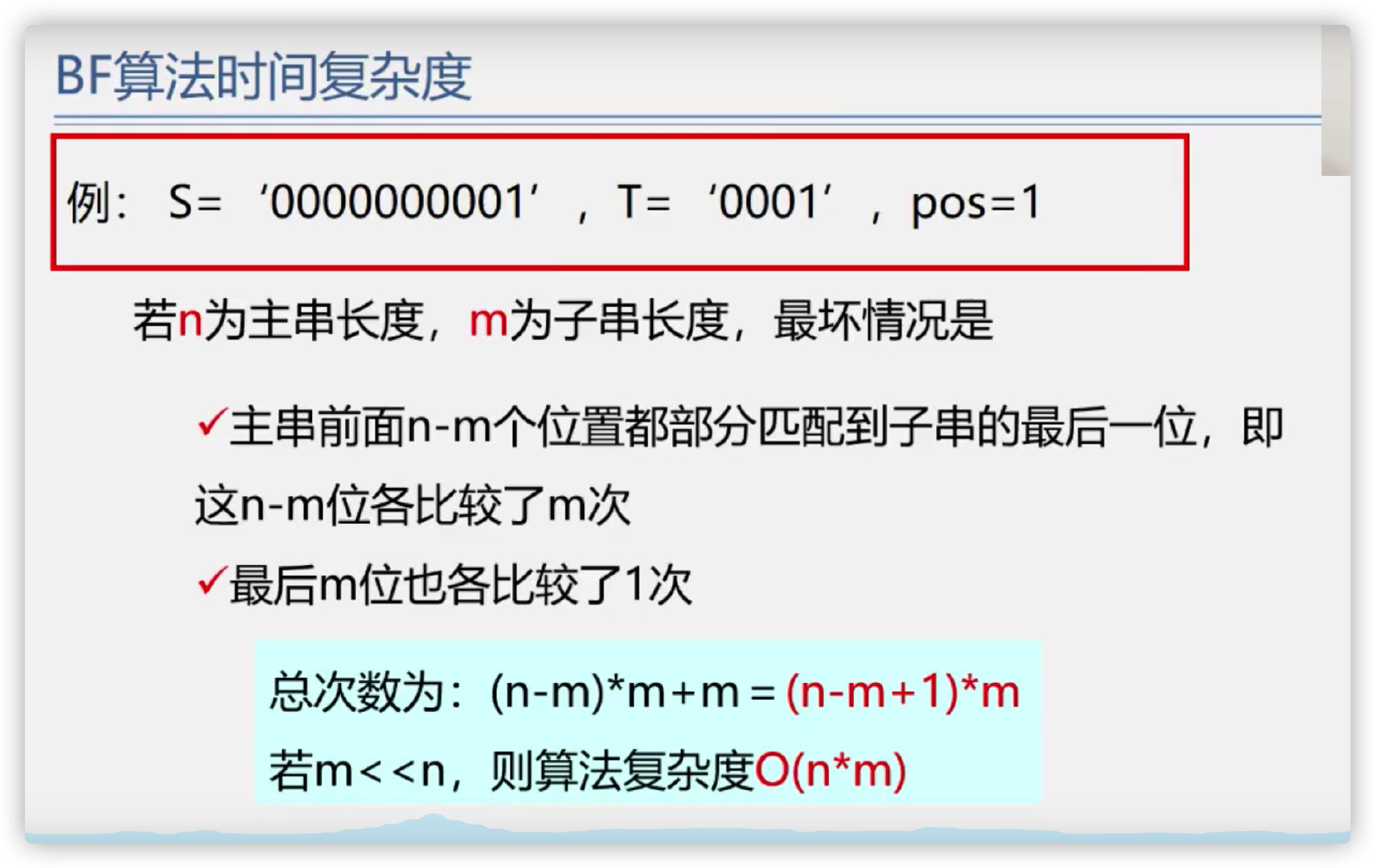
(3) BF algorithm

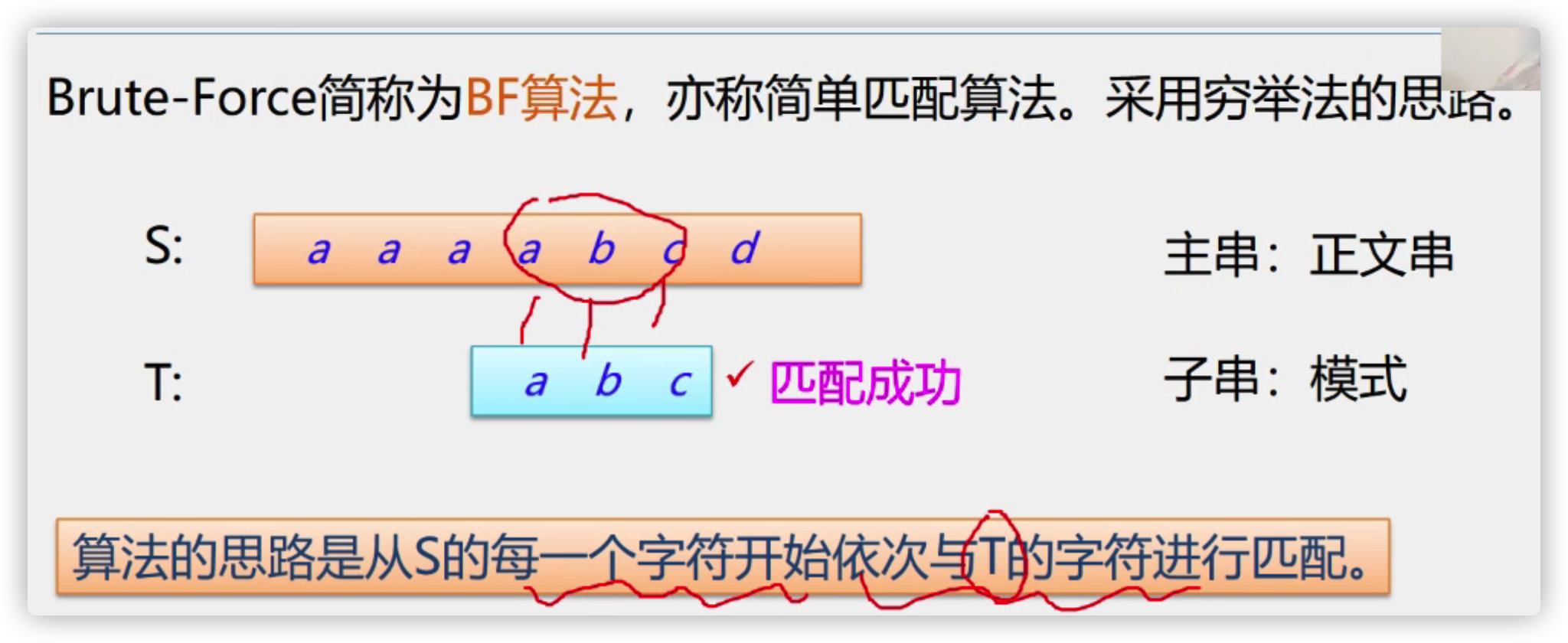
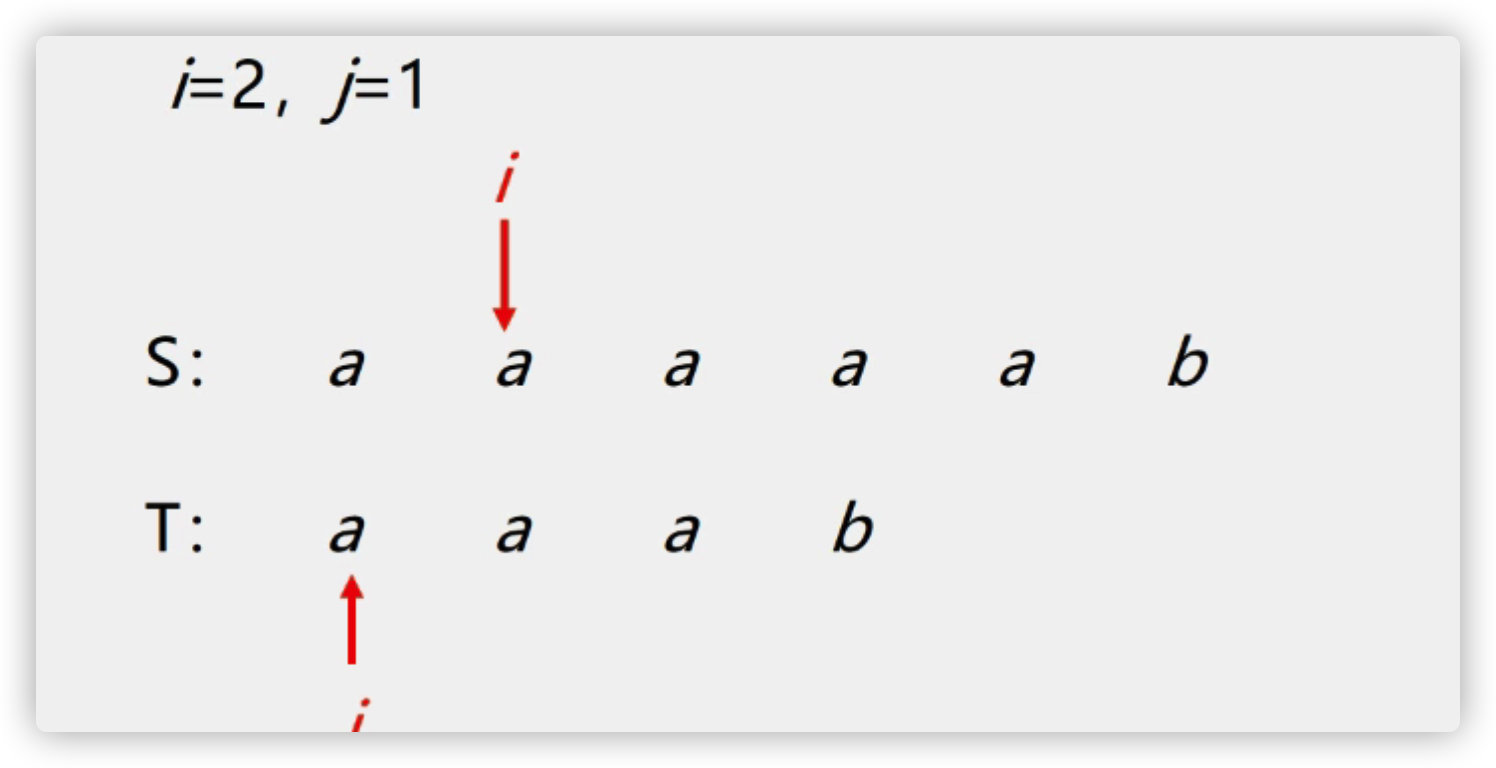
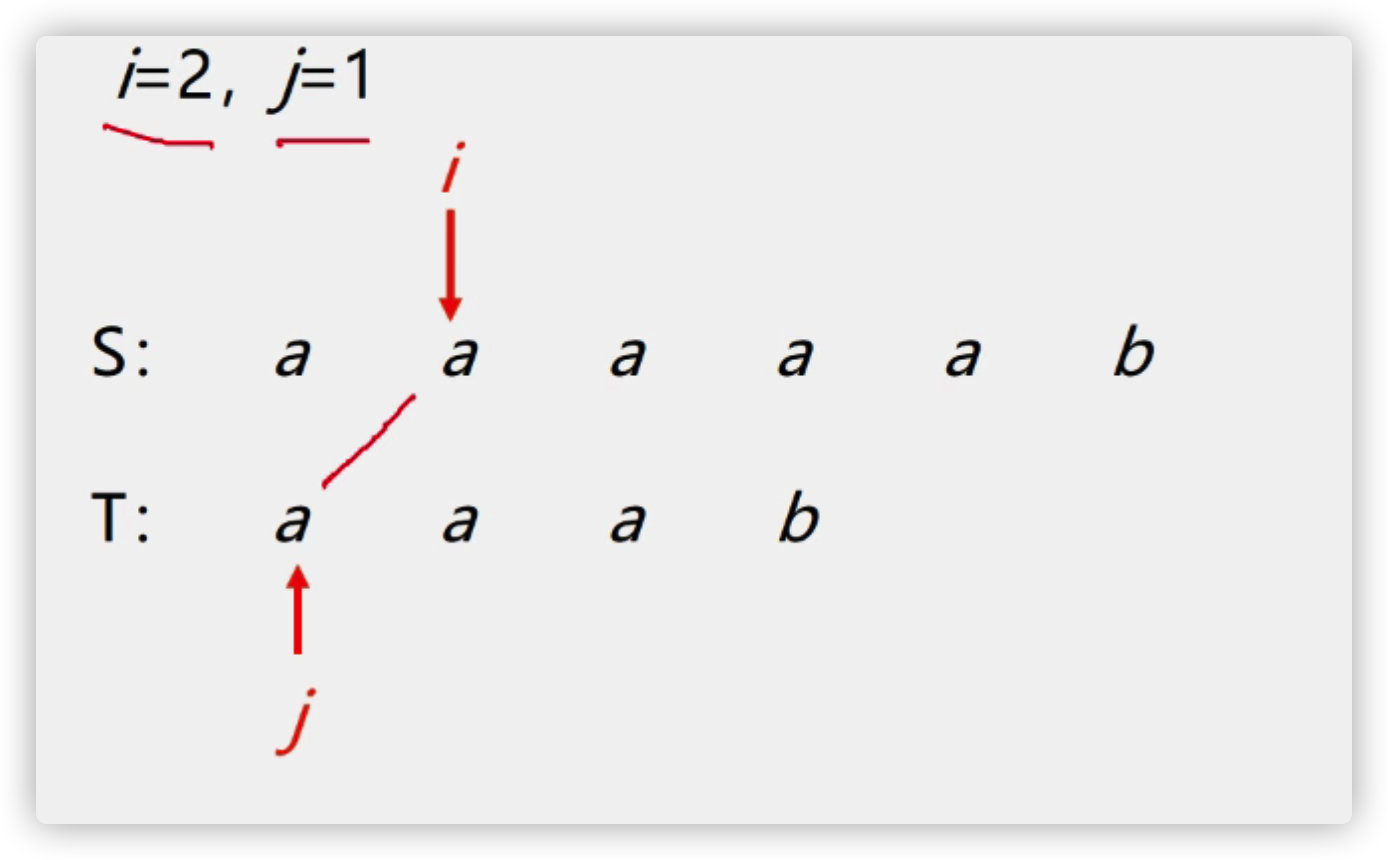
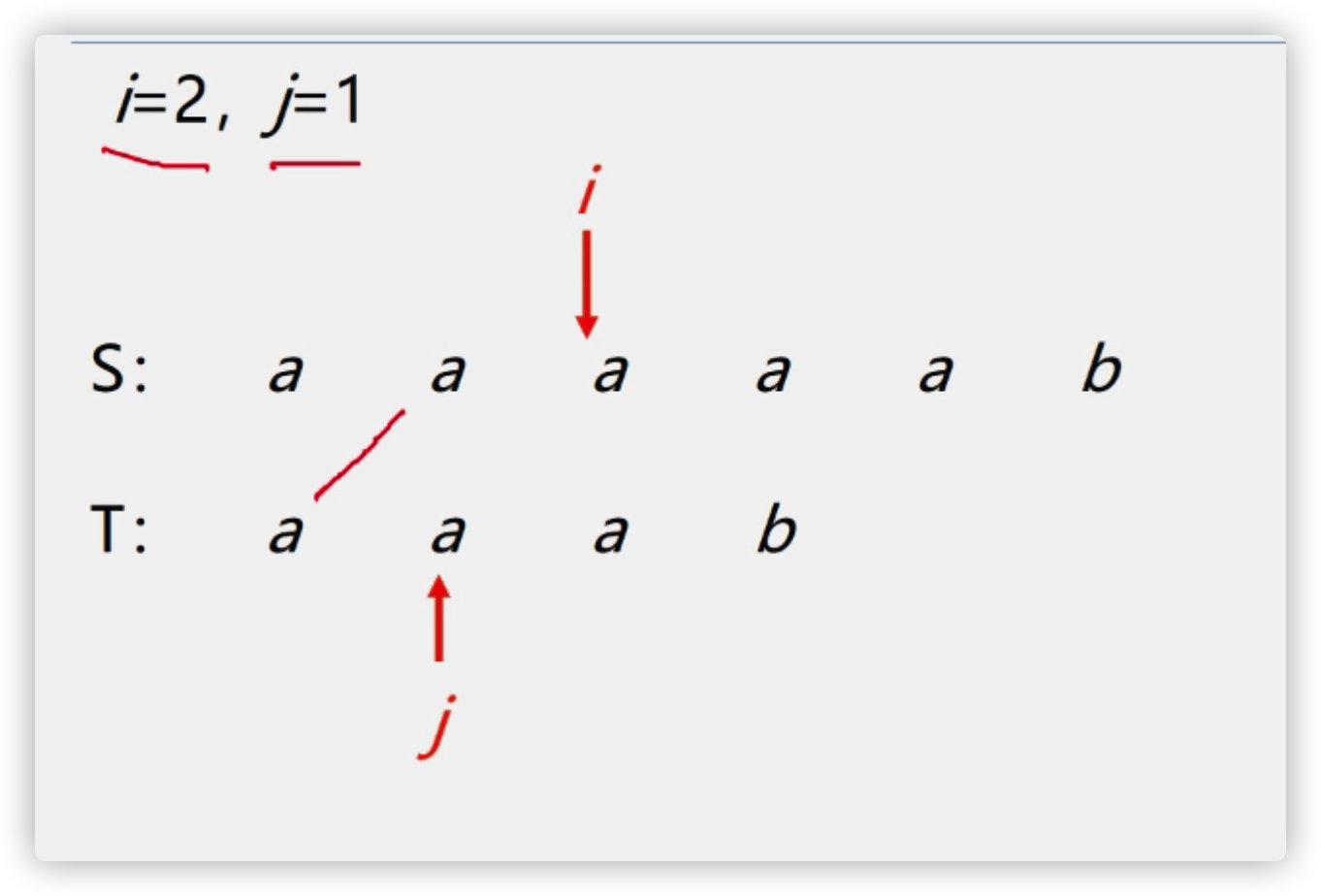
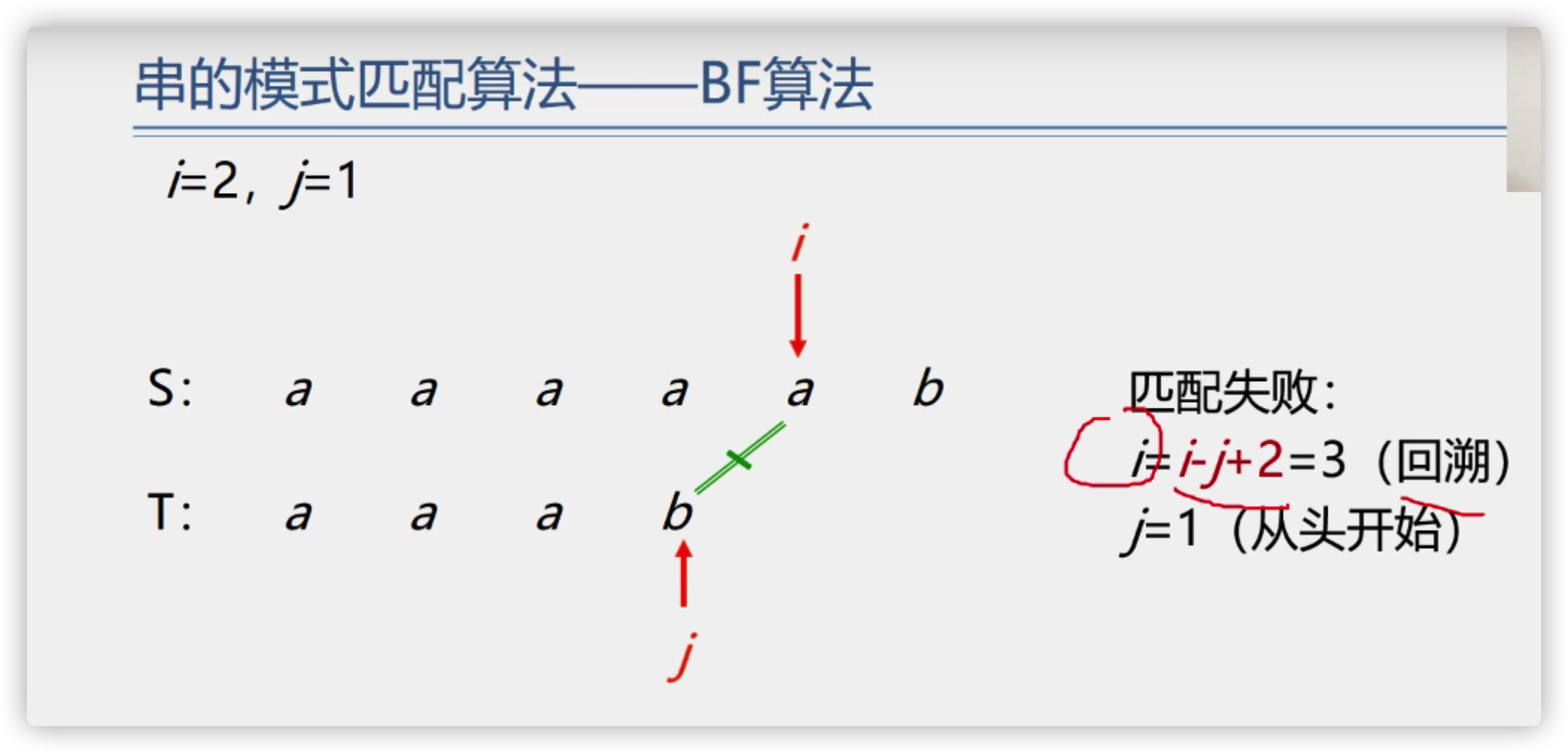
Find the code implementation from scratch

Find the code implementation from the specified location

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-r1gw9kup-1636095678706) (/ users / ouyangyansong / library / Application Support / typera user images / image-20211101195124408. PNG)]

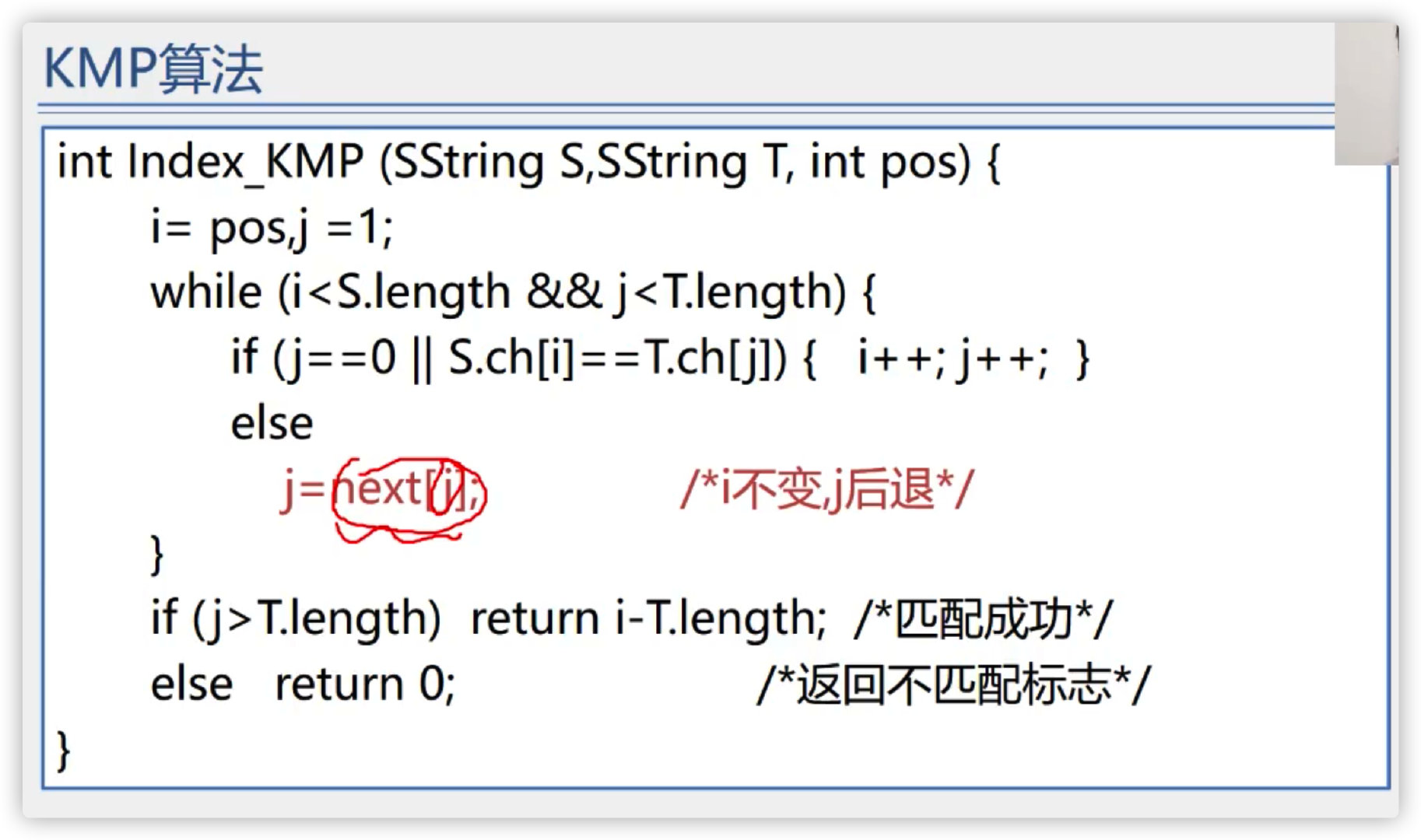
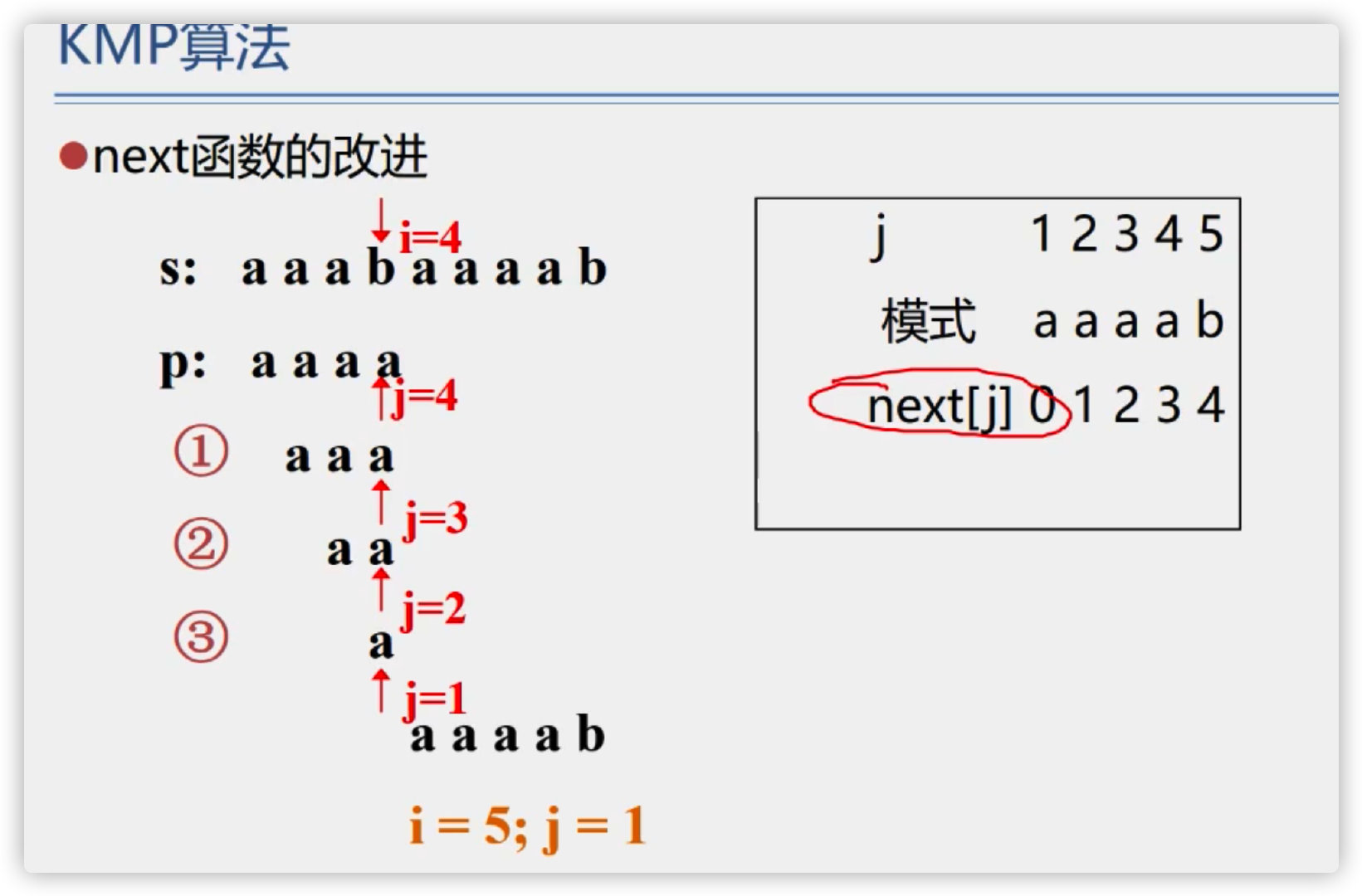
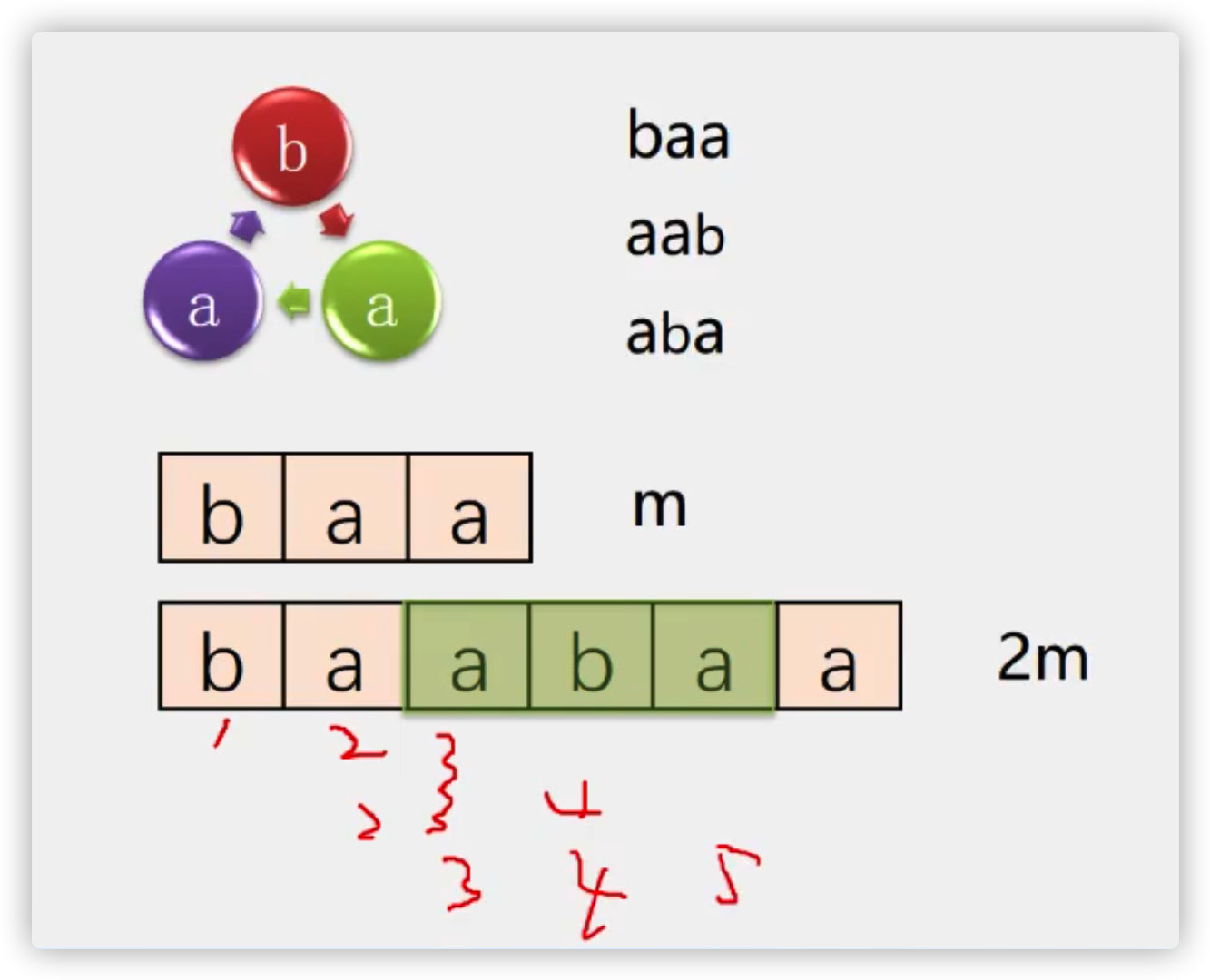
(4) KMP algorithm

I don't understand

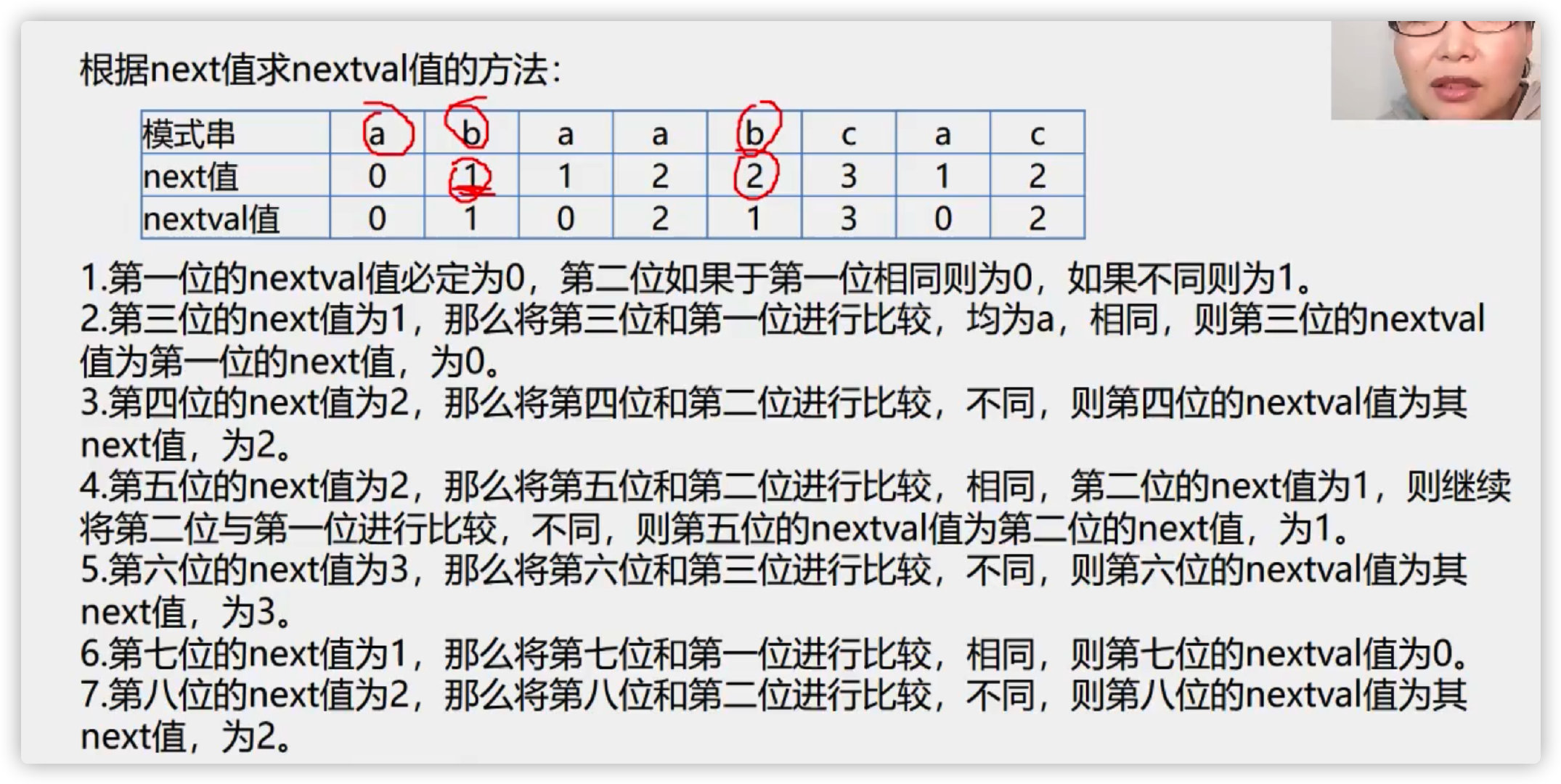
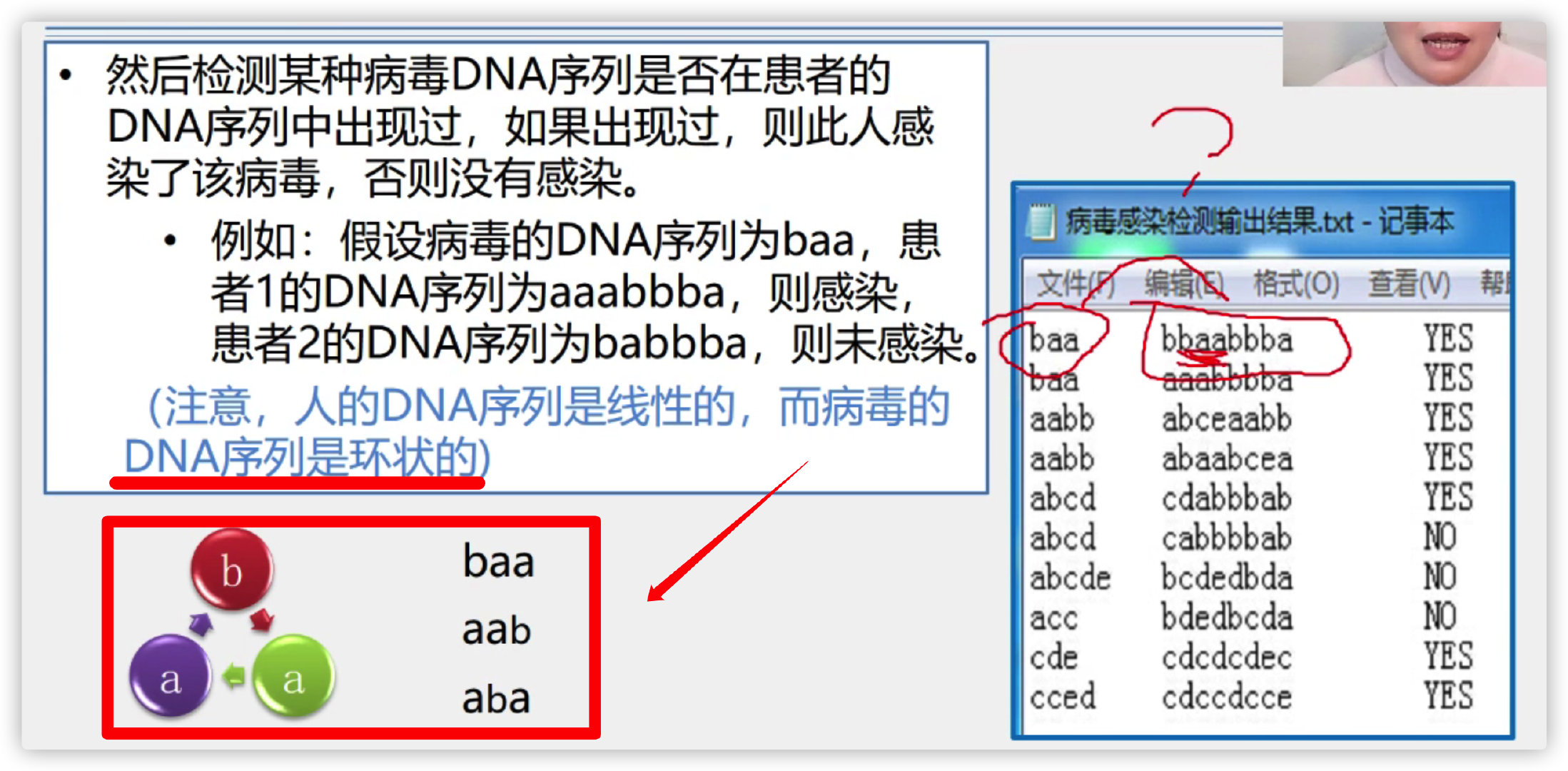
(5) Case - virus detection

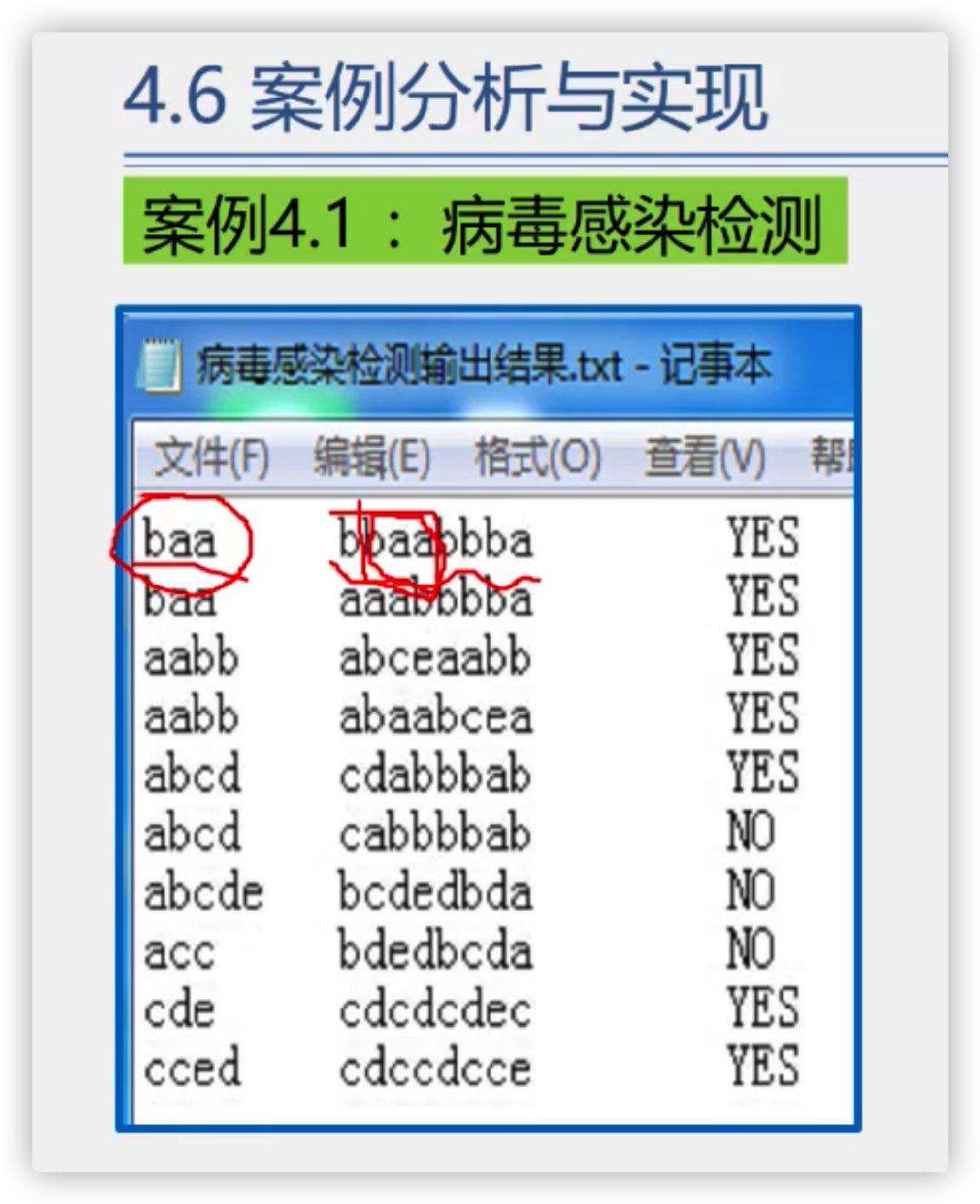
7. Array

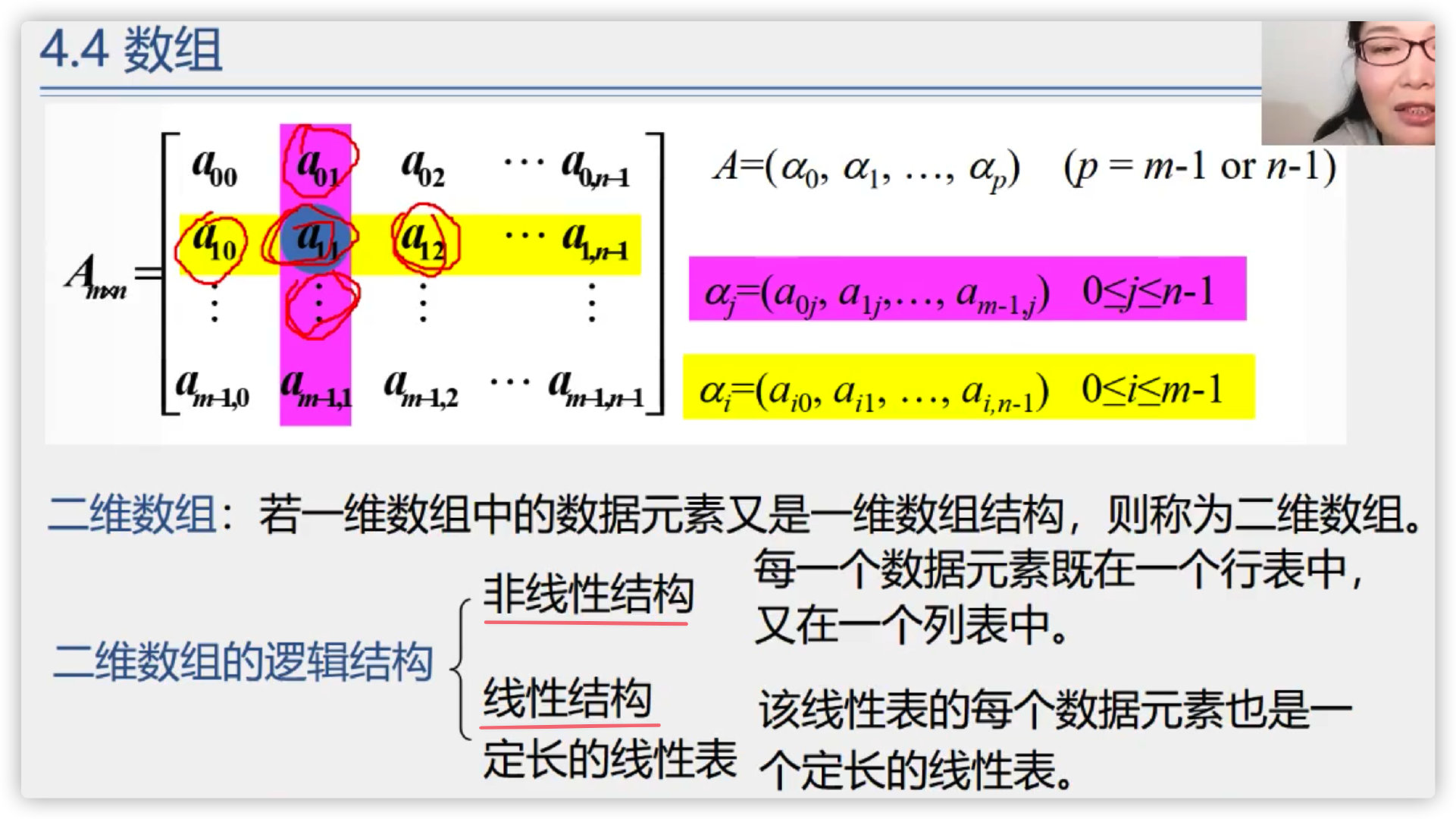
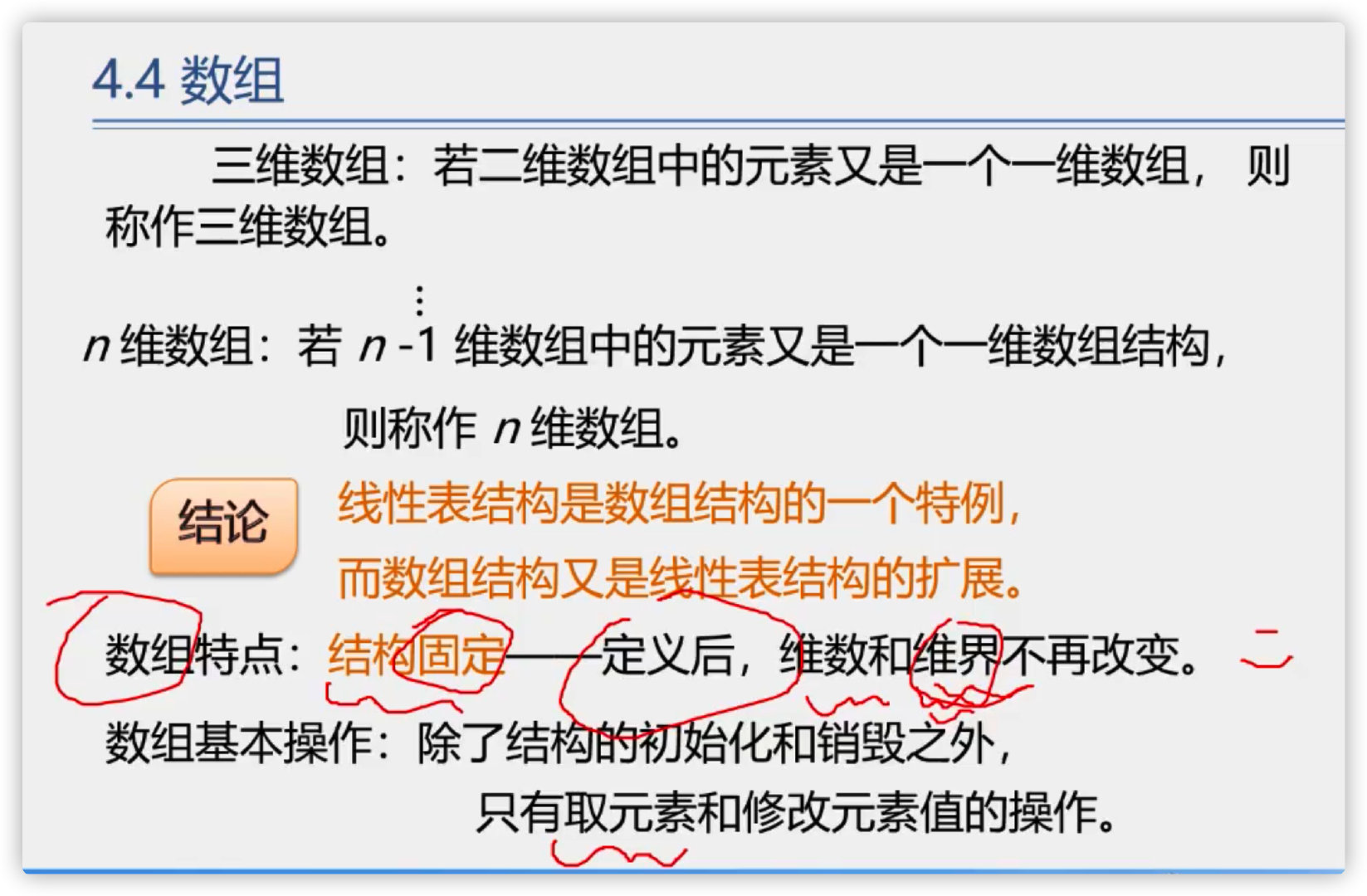
Definition: a collection of data elements of the same type arranged in a certain format

(1) One dimensional array

(2) Two dimensional array

Extremely special: it can be regarded as either linear structure or nonlinear structure

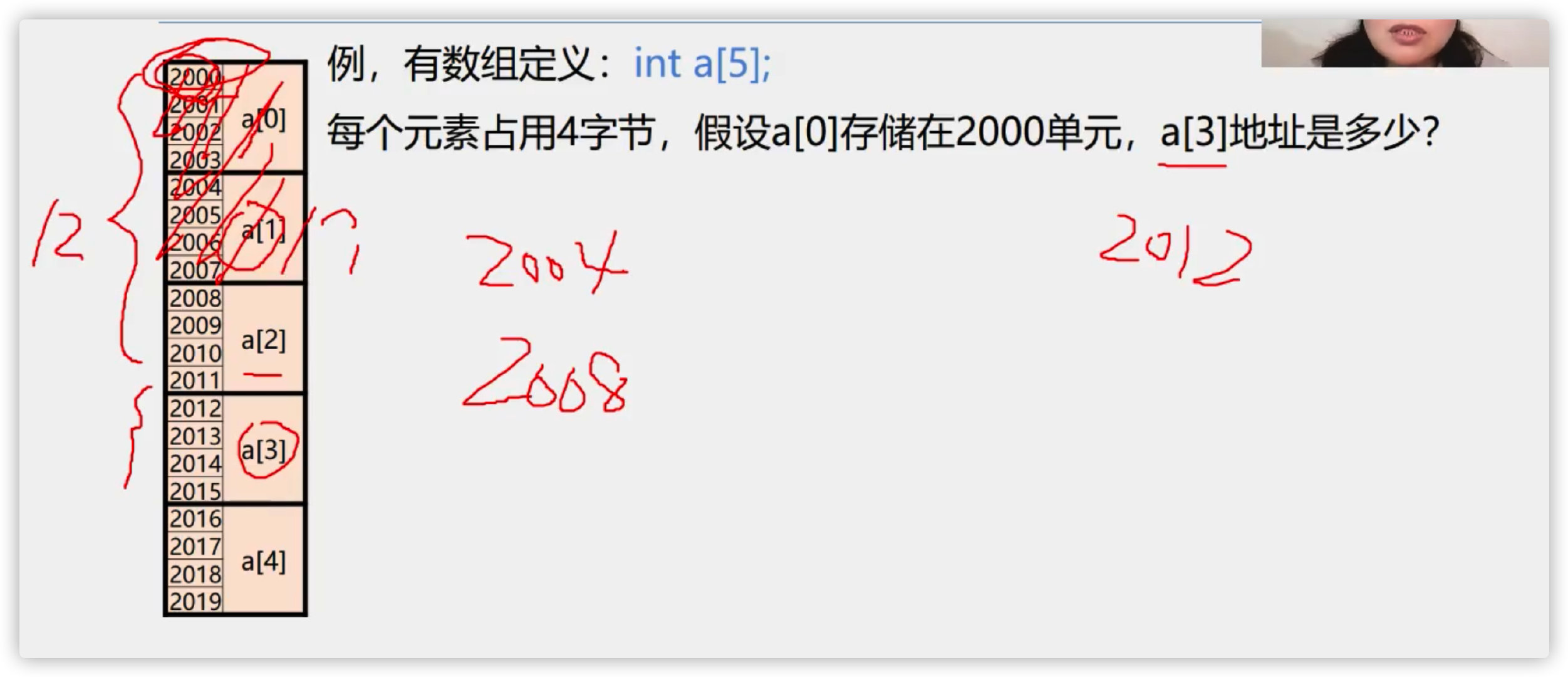
(3) Sequential storage of arrays

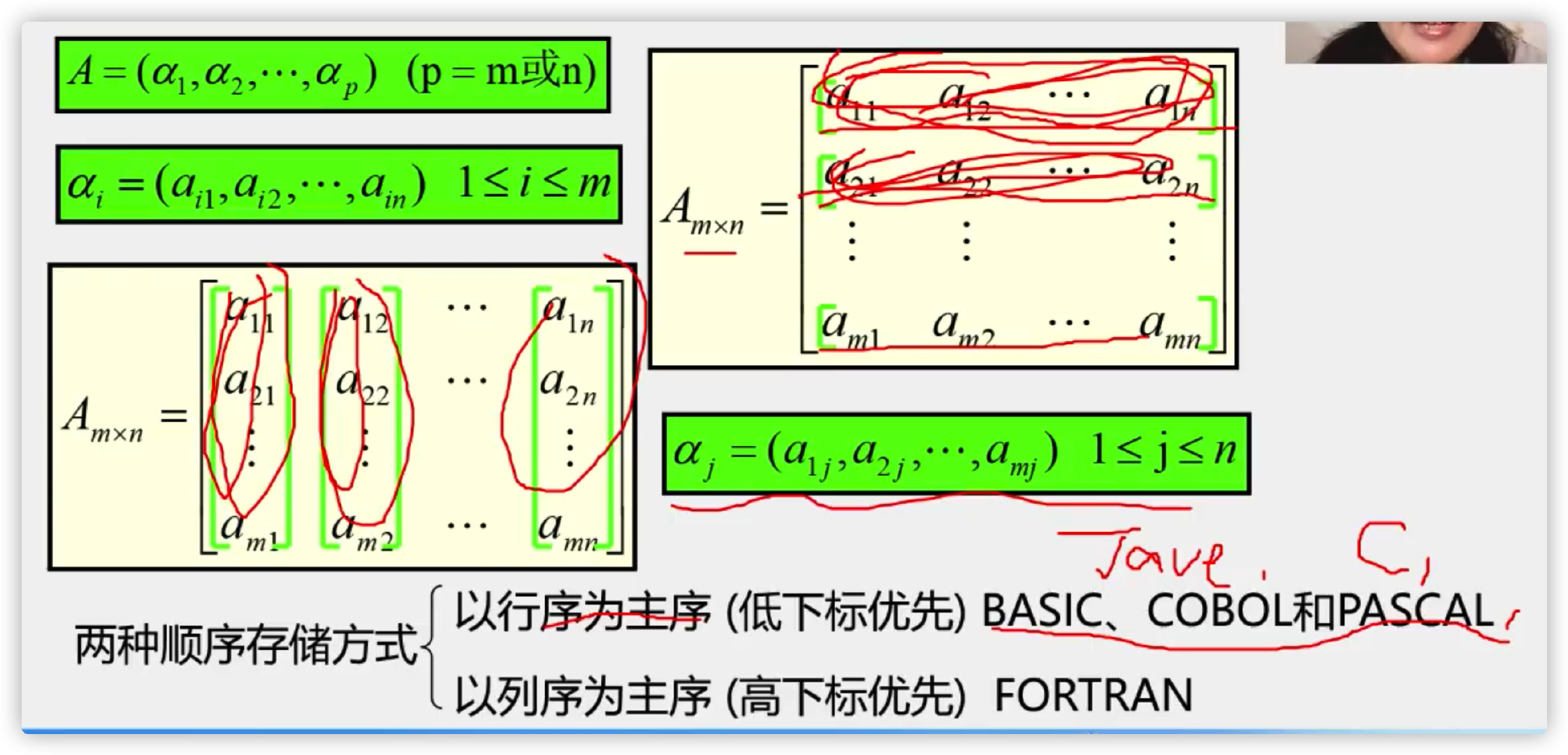
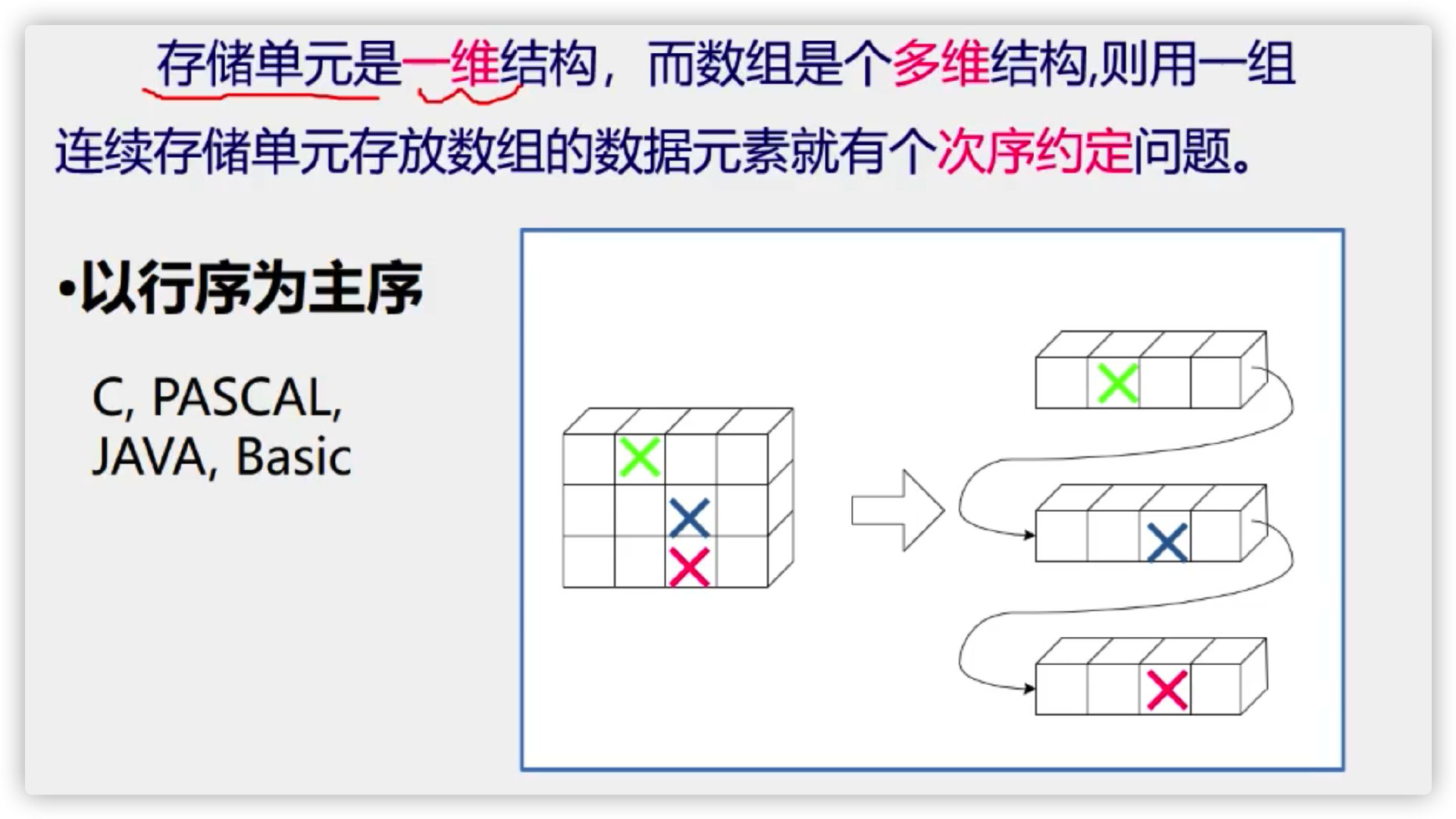
Row order is the main order

Column order is the main order

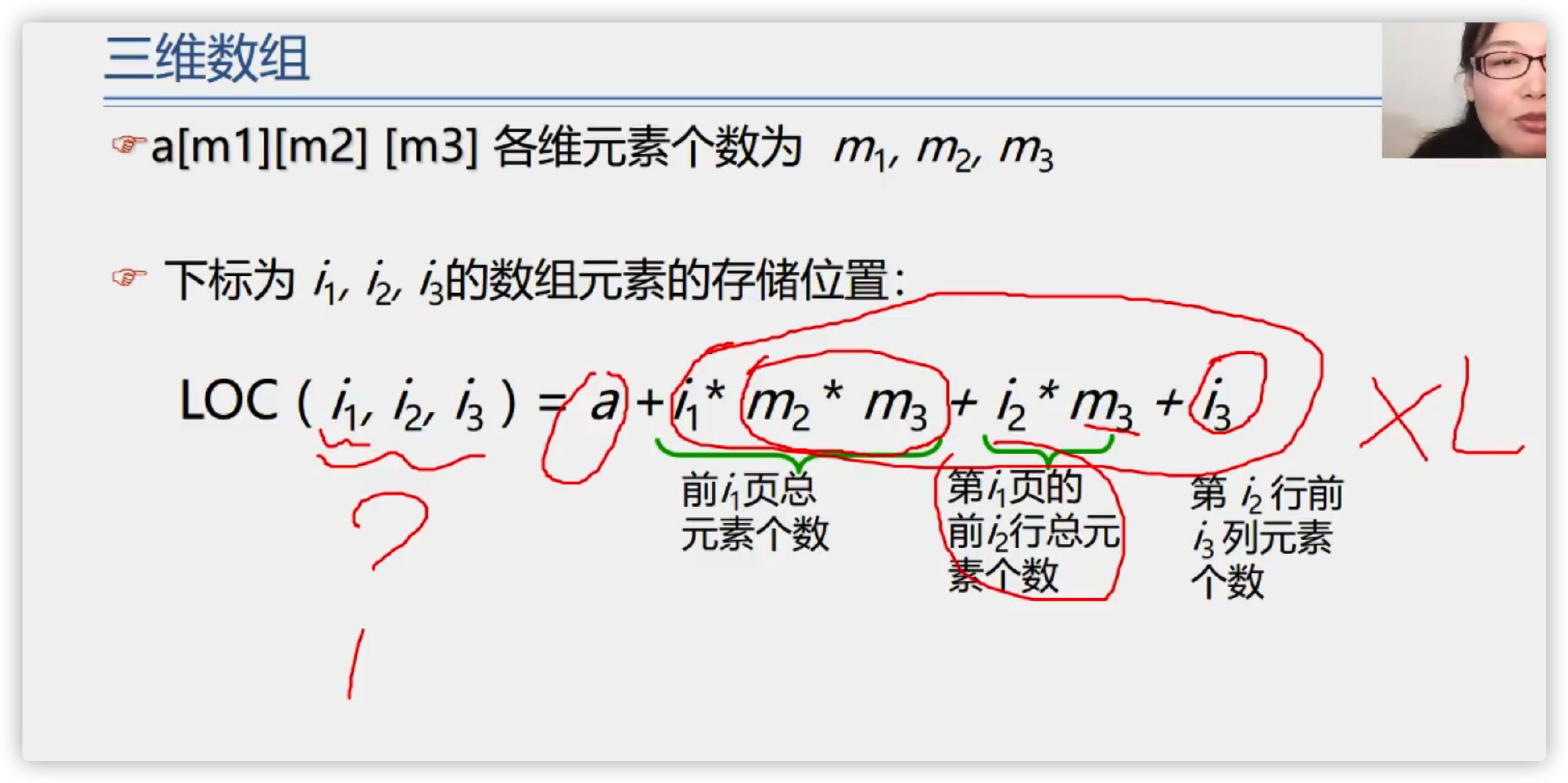
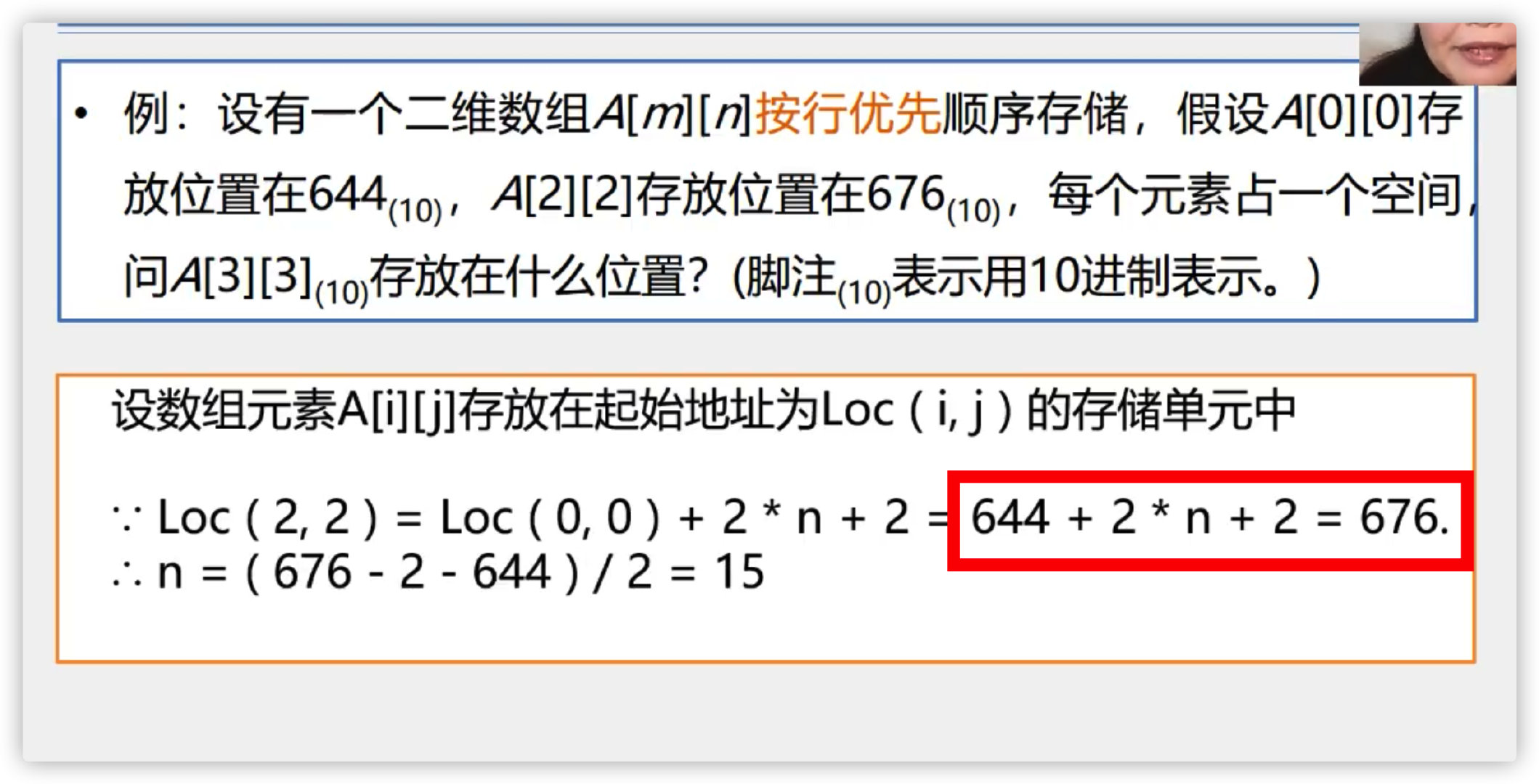
1. Compressed storage of special matrix

2. Symmetric matrix

3. Triangular matrix

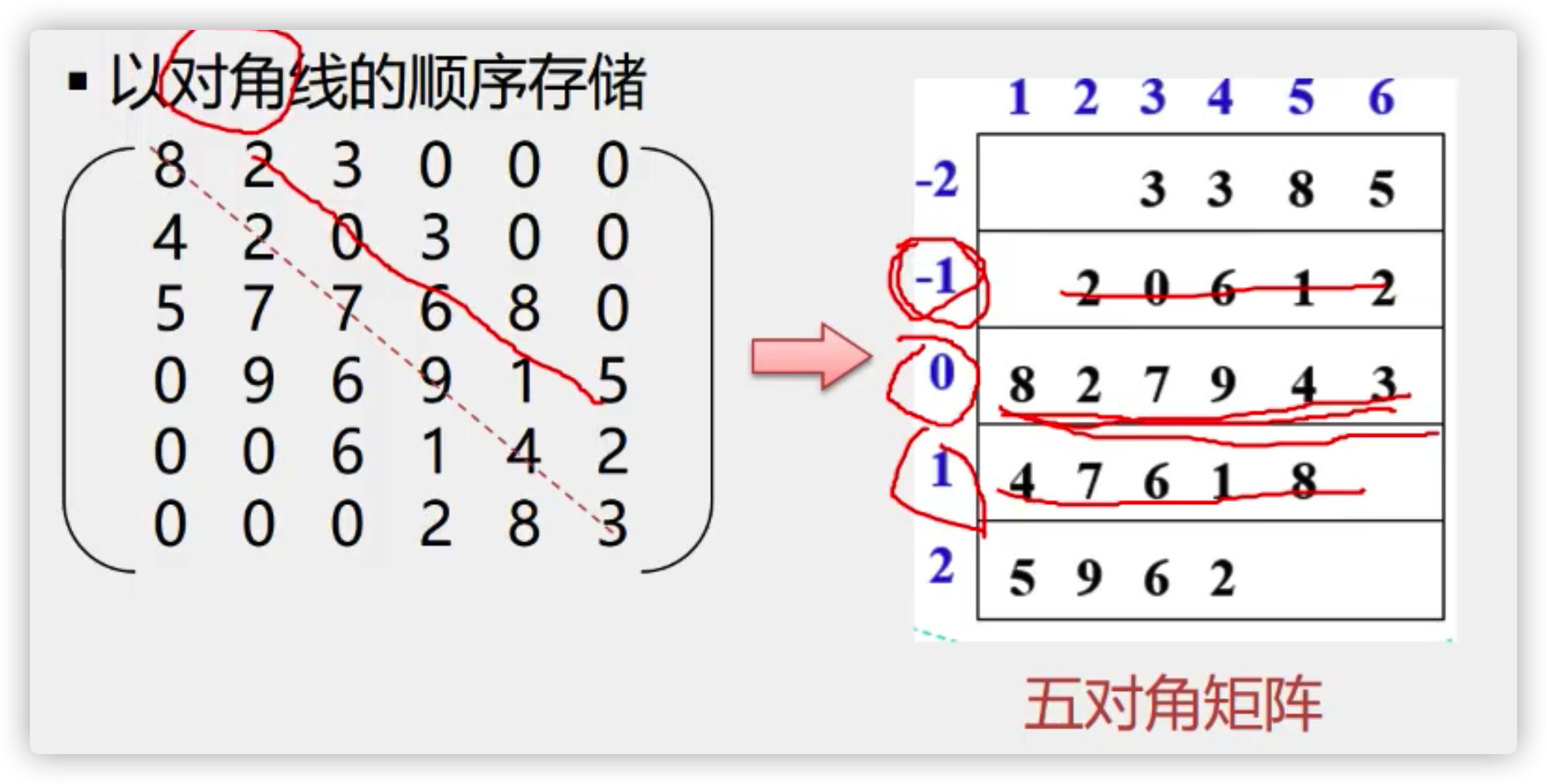
4. Sparse matrix

Triple sequence table

Linked storage structure - cross linked list

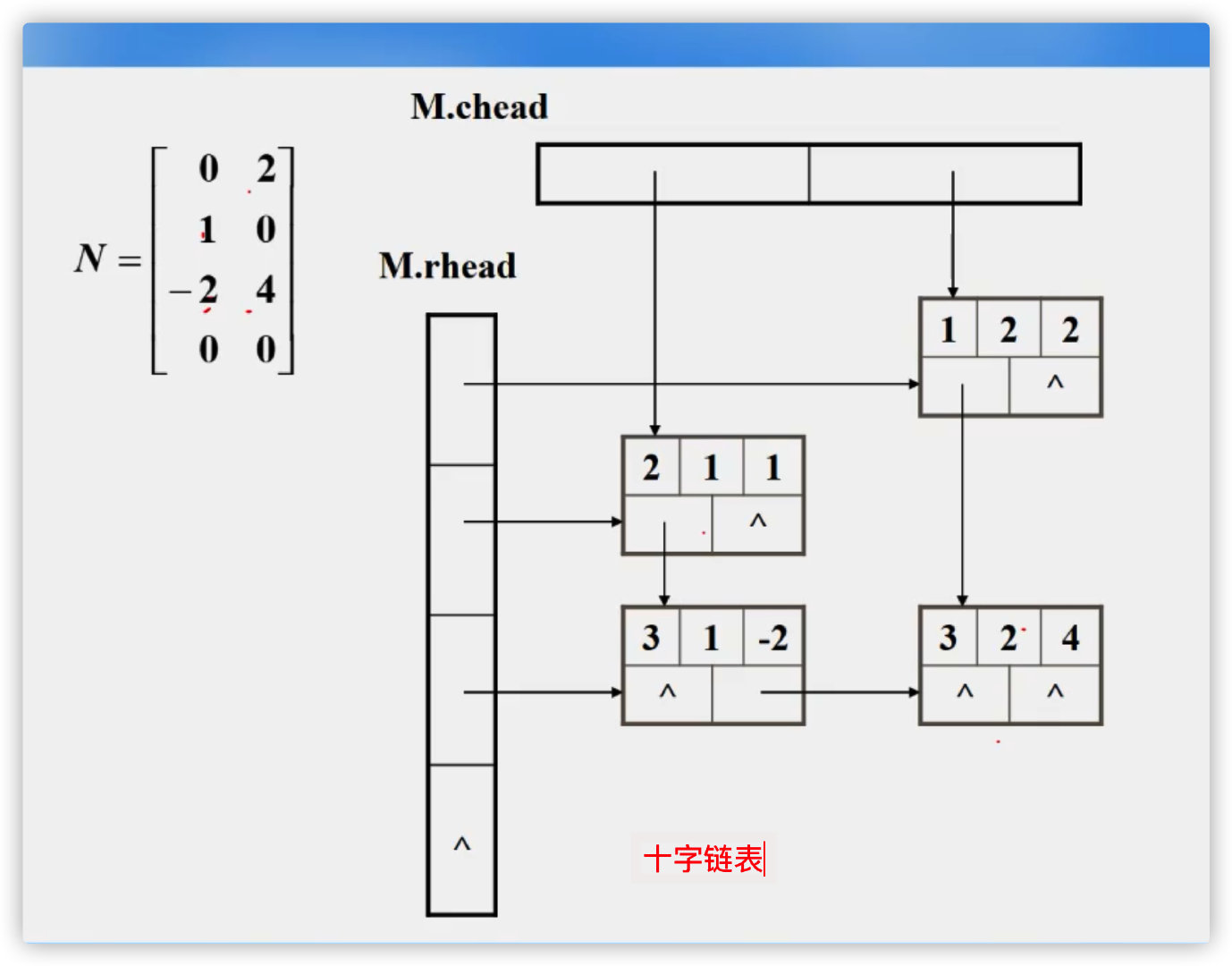
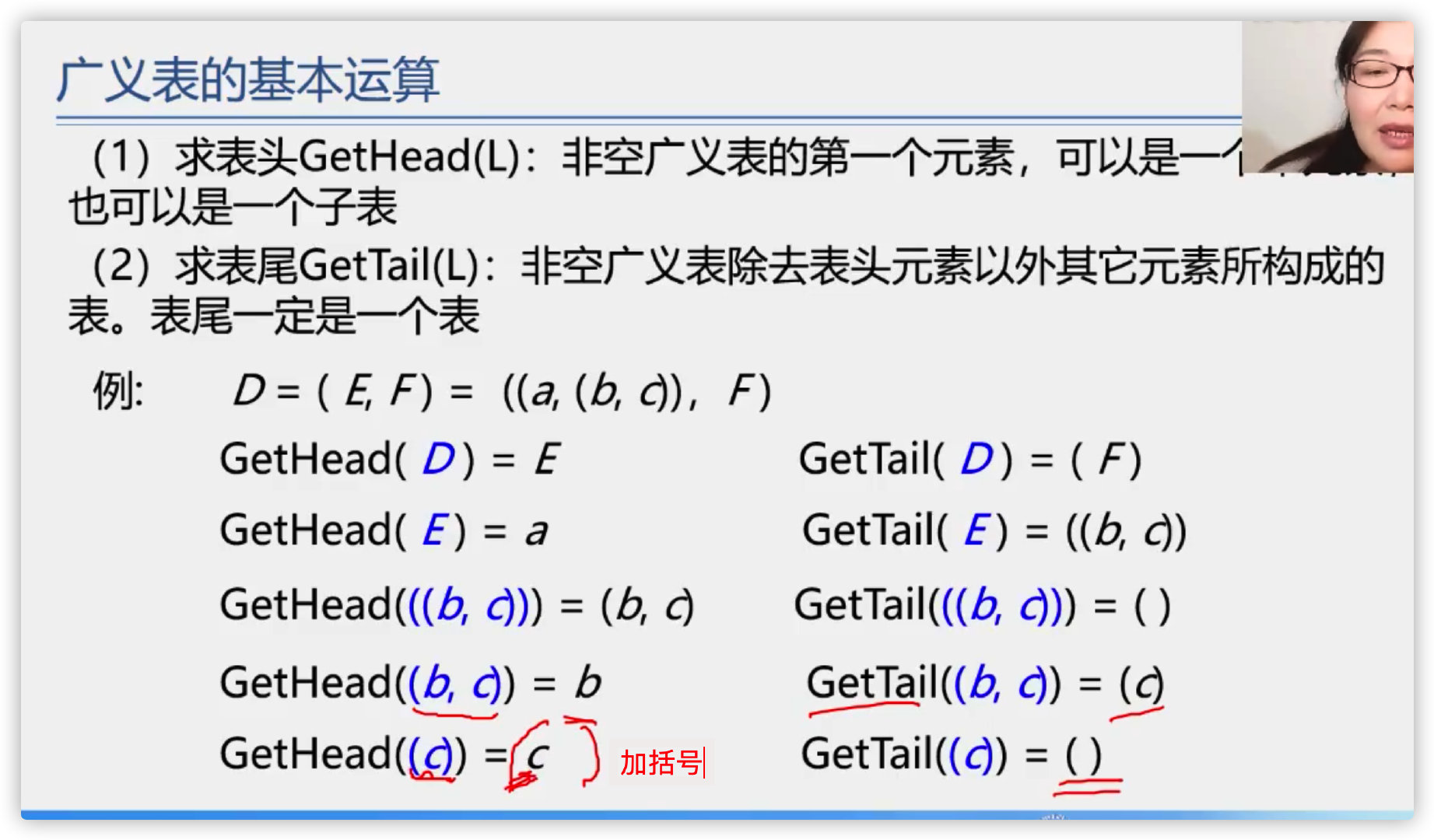
8. Generalized table

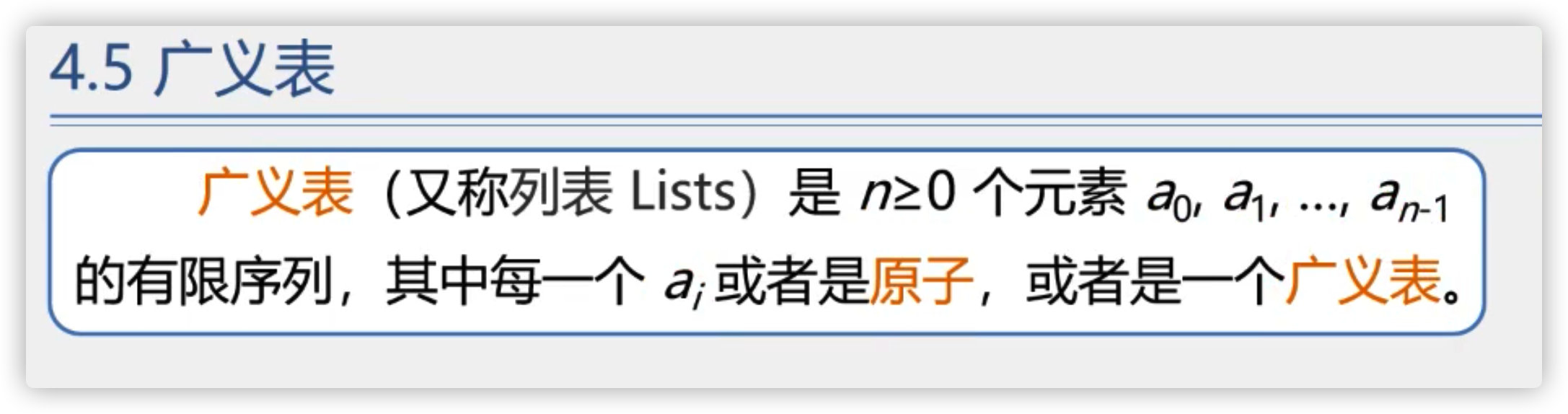
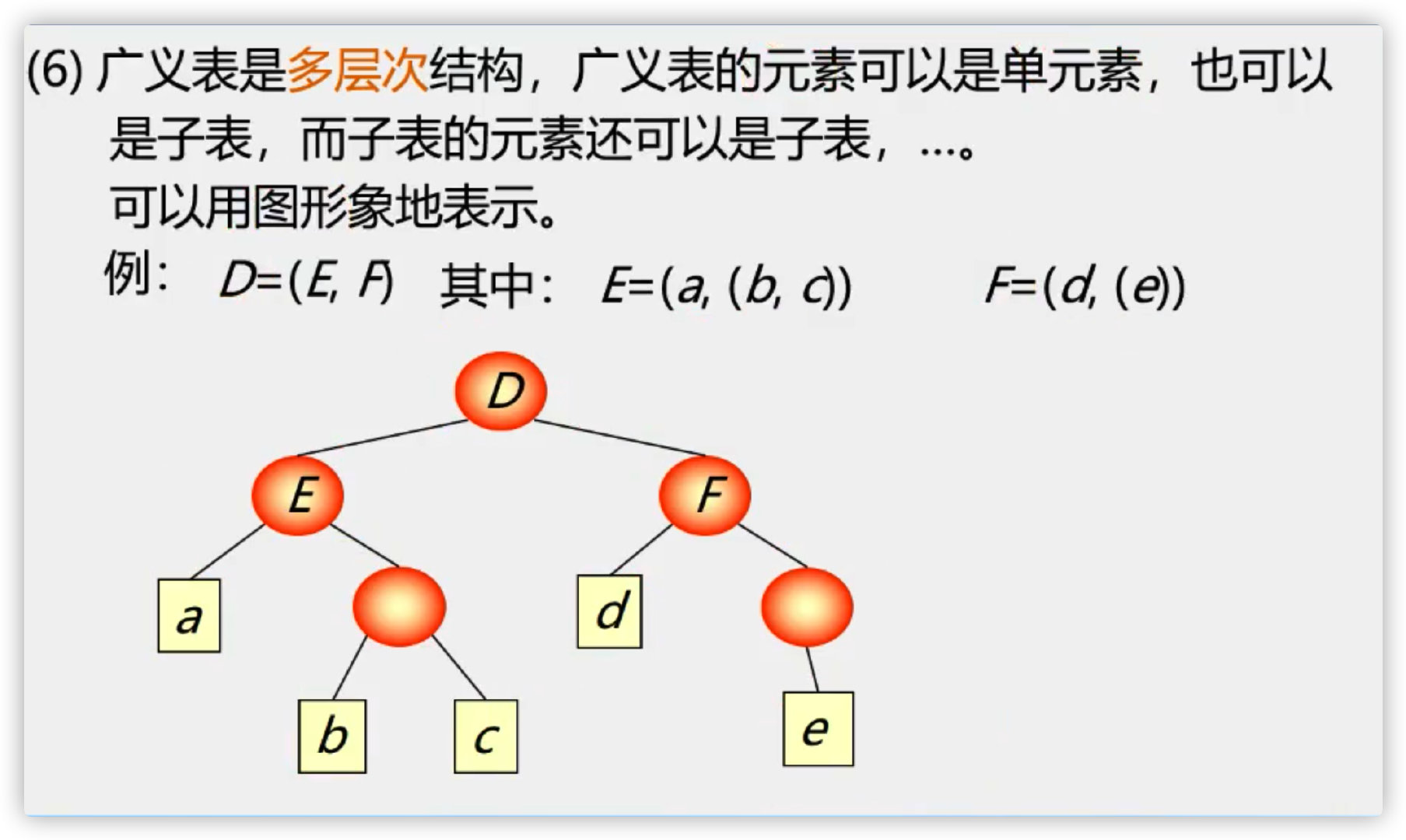
Basic operations of generalized tables

4, Nonlinear structure

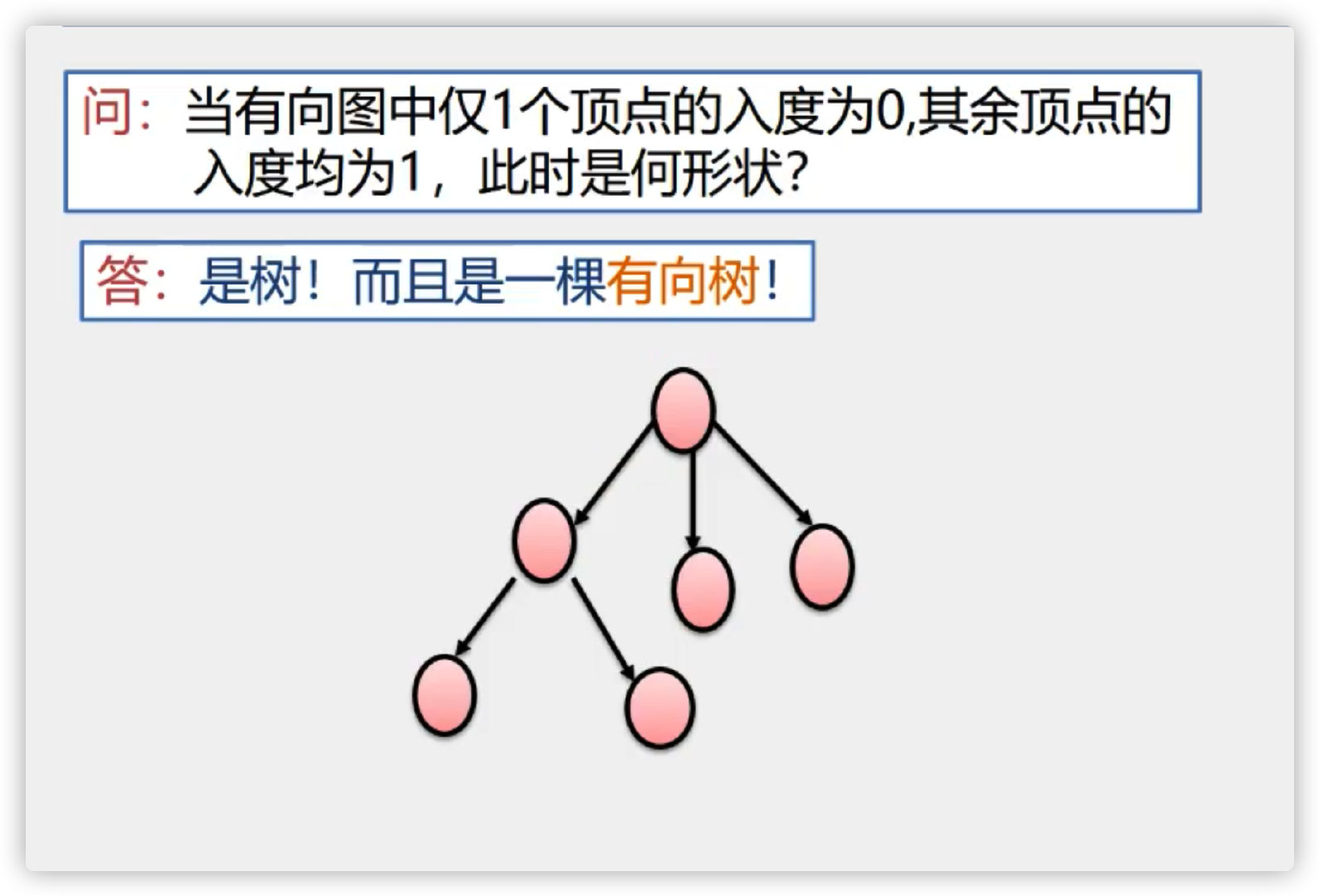
1. Tree

To learn:

B tree and B + tree

Stop B and take the course of the chapter on trees taught by Mr. Geng of Northwestern University

1) Definition of tree

Definition: 1. There is only one node called root

2. There are several disjoint subtrees, which are also a tree

Popular definitions: 1. A tree is composed of nodes and edges

2. Each node has only one parent node, but can have multiple child nodes

3. Except for one node, which has no parent node, this node is called the root node

Technical Term

• node

  • Parent node
  • Child node

• descendants

  • male cousins

• Depth: the number of floors from the root node to the bottom node is called depth - similar floors

• **Leaf node: * * node without child nodes

• Non terminal node: actually, it is a non leaf node

• Root node

• **Degree: * * the number of child nodes is called degree

2) Tree classification

1. General tree: the number of any child node is unlimited

2. Binary tree: the maximum number of child nodes of any node is 2, and the position of child nodes cannot be changed!

Classification of binary tree:
					1,General binary tree
					2,Full binary tree:On the premise of not increasing the number of layers of the tree, a binary tree that cannot add one more node is a full binary tree
					3,Complete binary tree: if the knowledge deletes several consecutive nodes at the bottom and right of the full binary tree, the binary tree formed in this way is a complete binary tree

3. Forest: a collection of n disjoint trees

3) Storage of and trees

Storage of trees: nonlinear – > linear

(1) Storage of binary tree:

1. Continuous storage (full binary tree)

2. Linked Storage

(2) Storage of general tree

1. Parental representation

It's easier to find parents than children

1. Child representation

2. Parent child representation

It is convenient to find both parent and child nodes

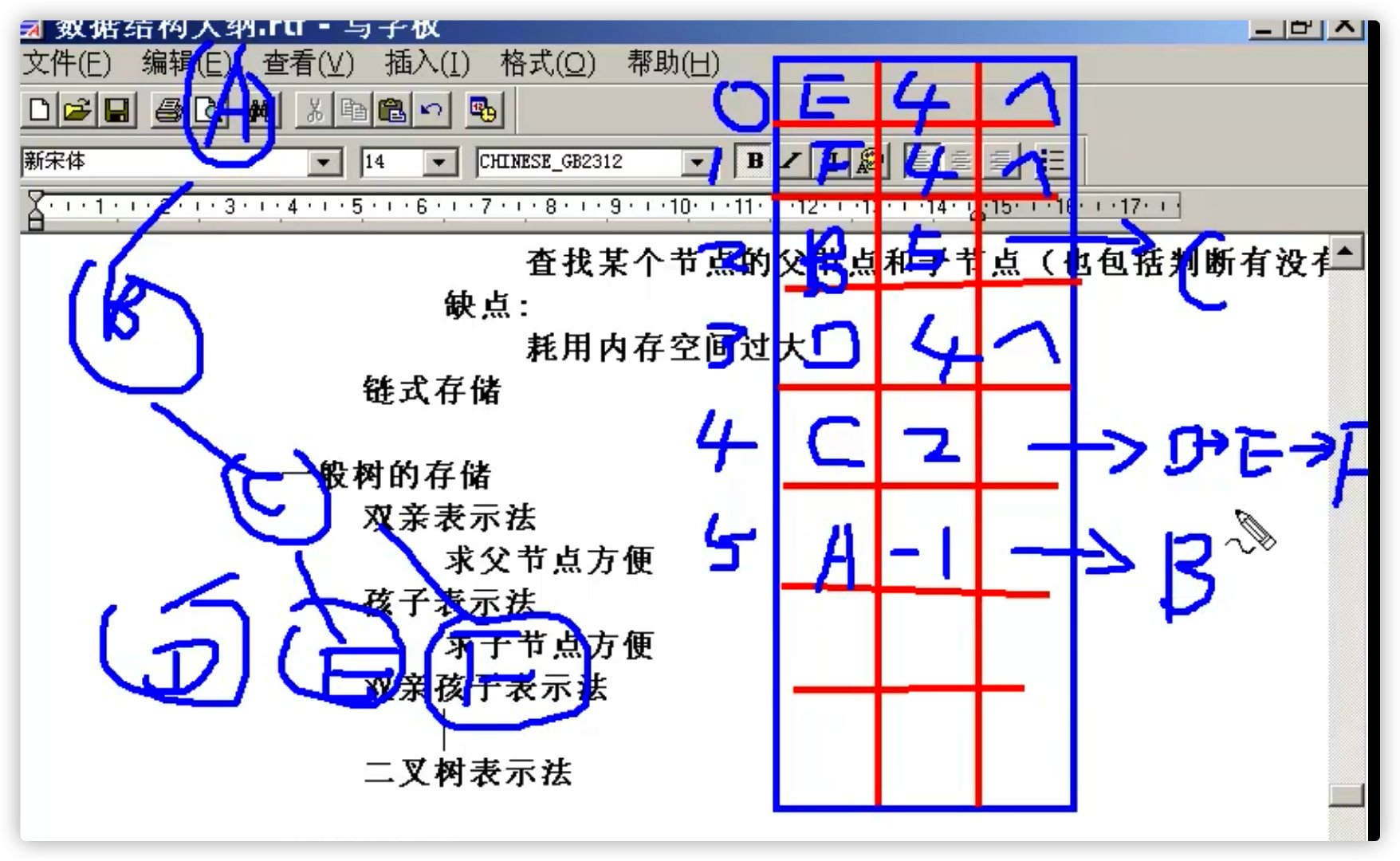
1. Binary tree representation

   Convert an ordinary tree into a binary tree pair for storage

Specific conversion method:

Try to ensure that the left pointer field of any node points to its first child and the right pointer field points to its brother. As long as this condition can be met, an ordinary number can be transformed into a binary tree

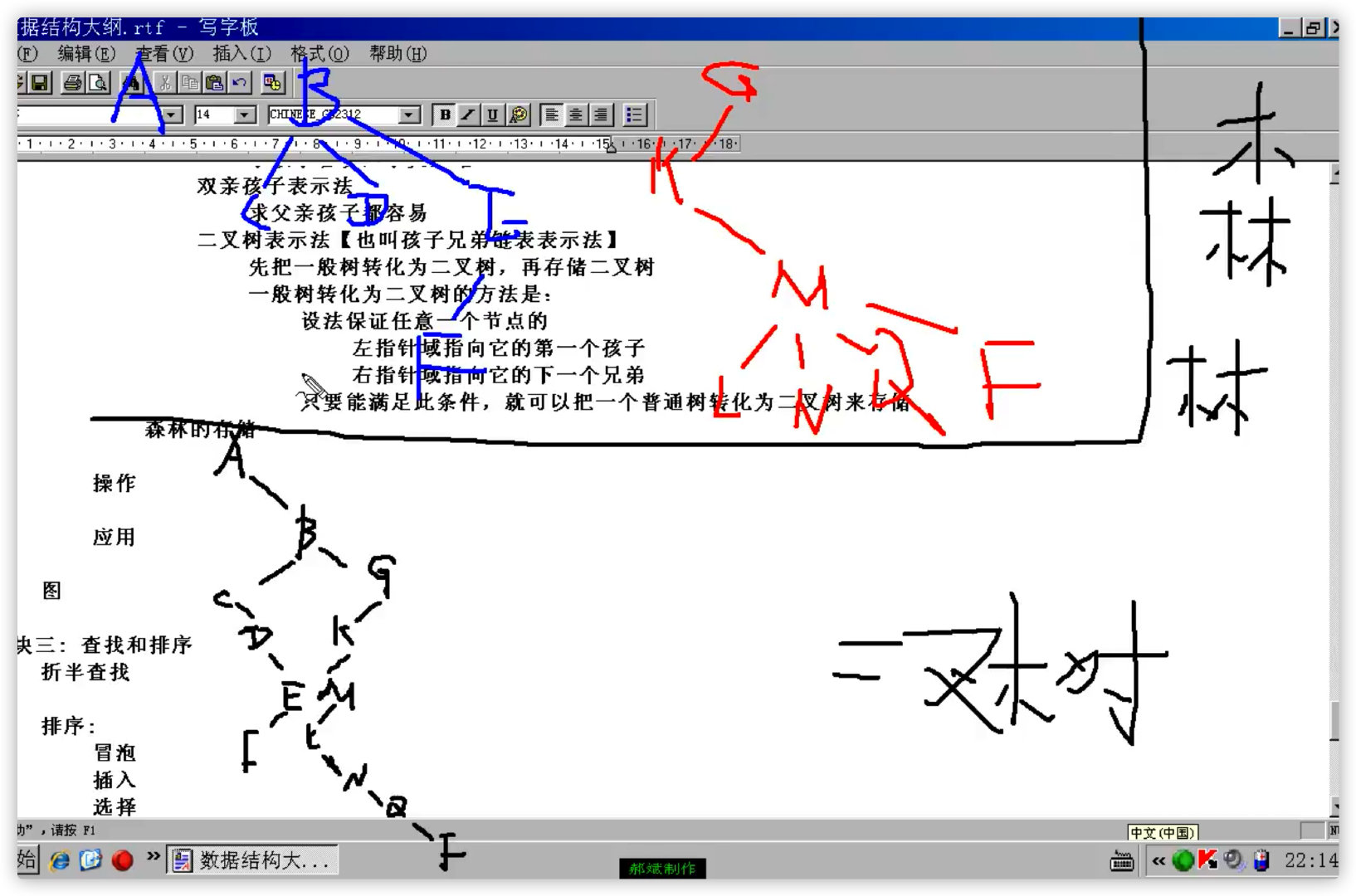
3) , forest

Convert tree to binary tree

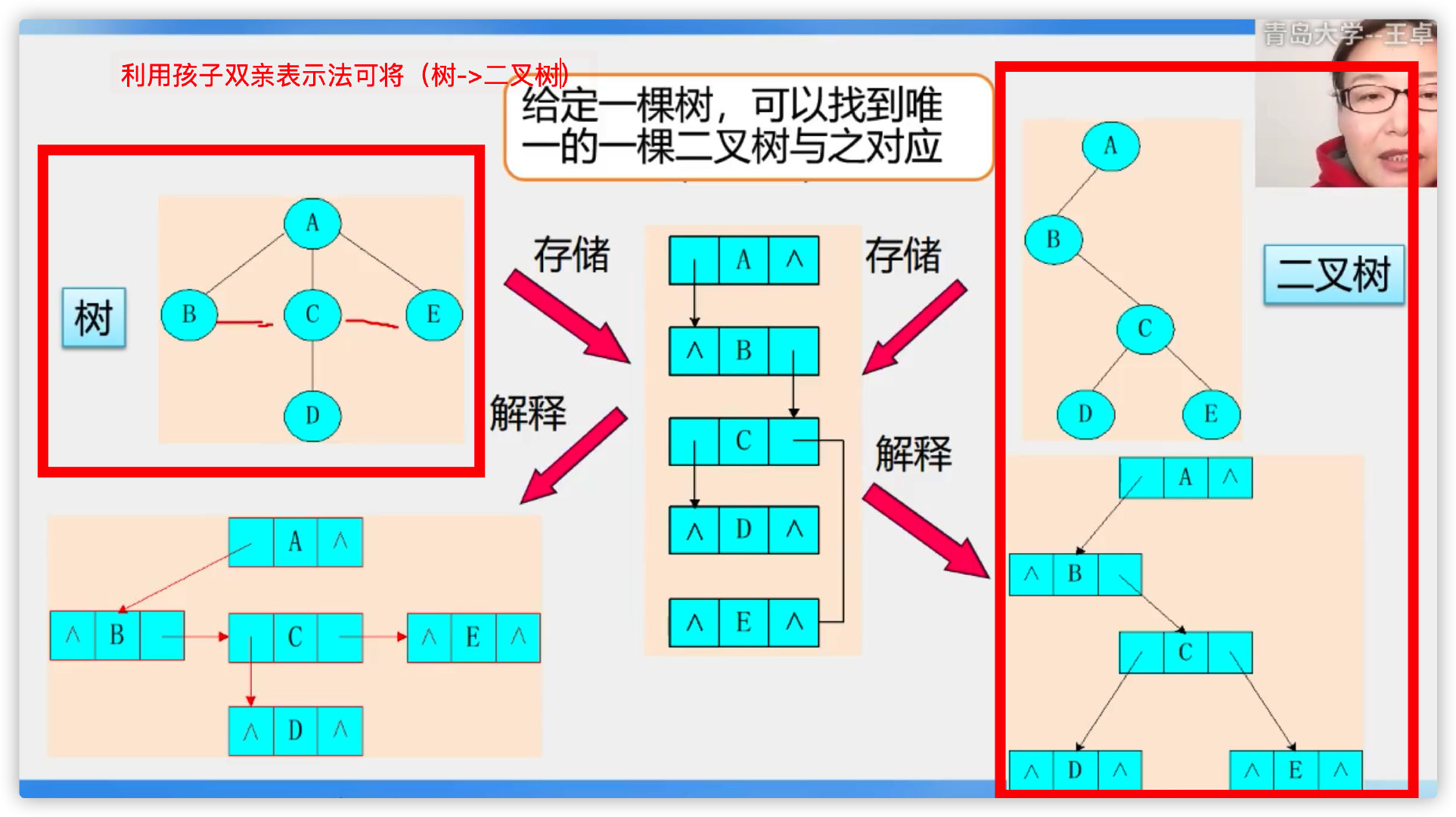
Pithy formula:

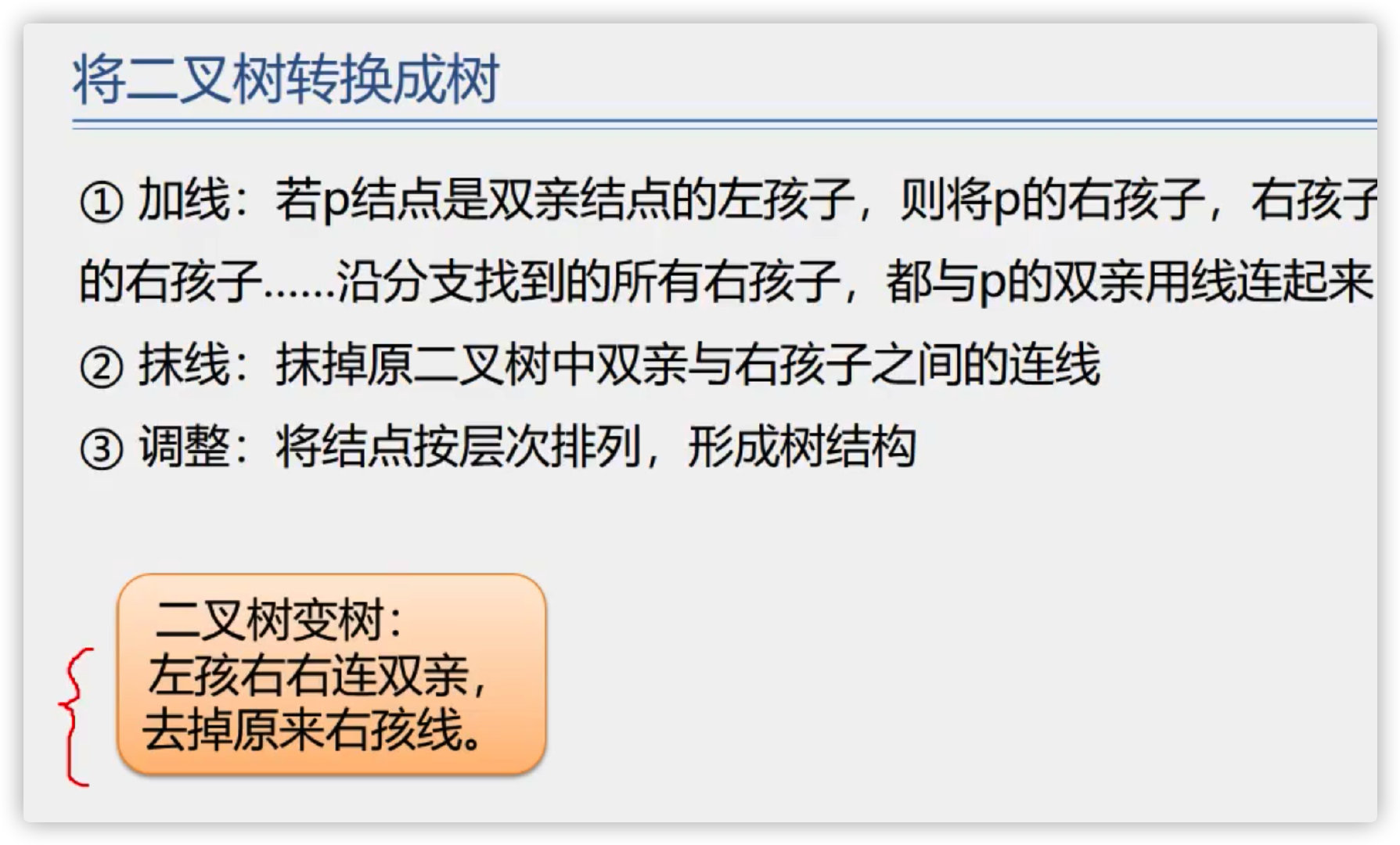
Binary tree into tree

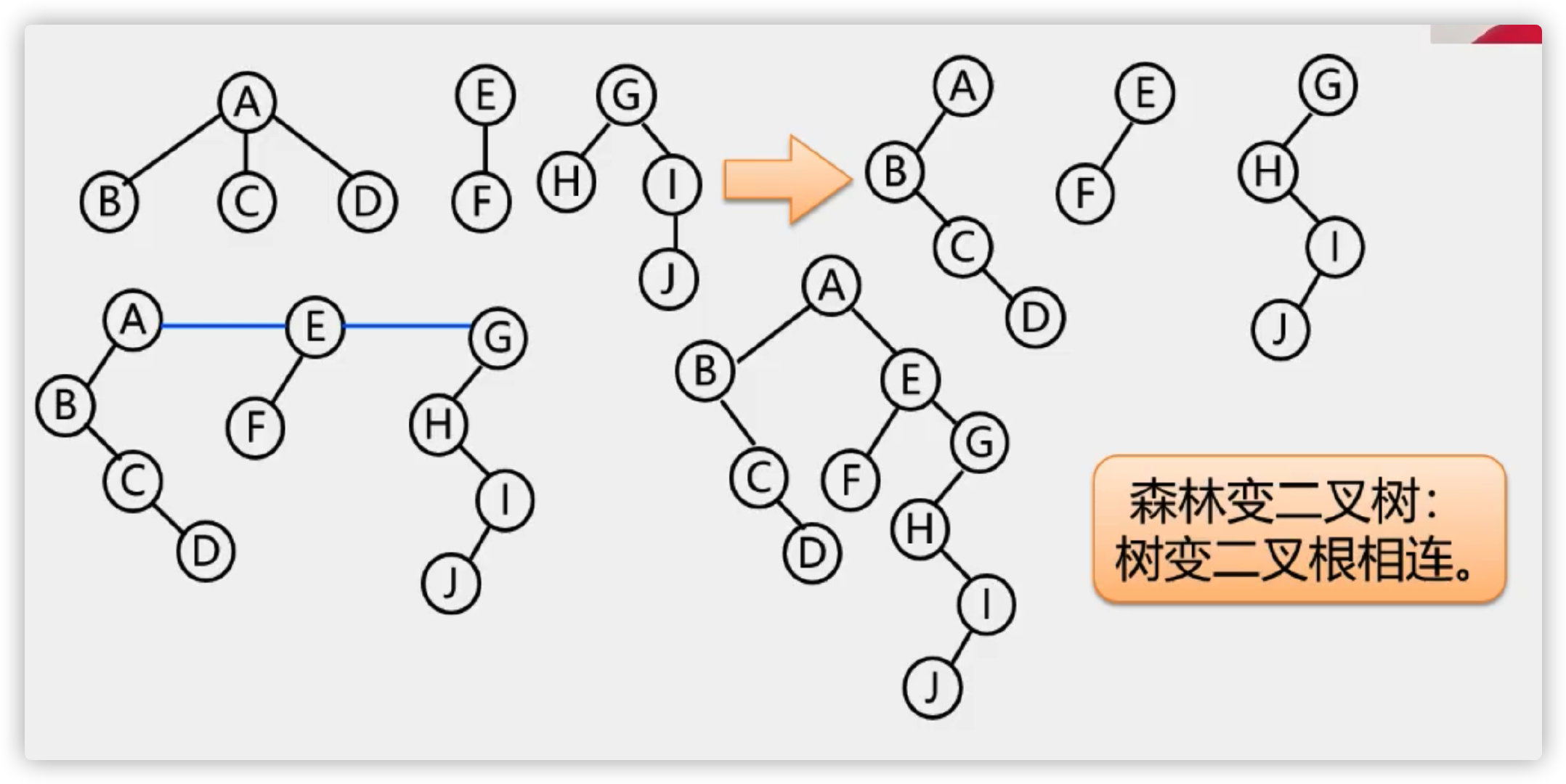
The forest turned into a binary tree

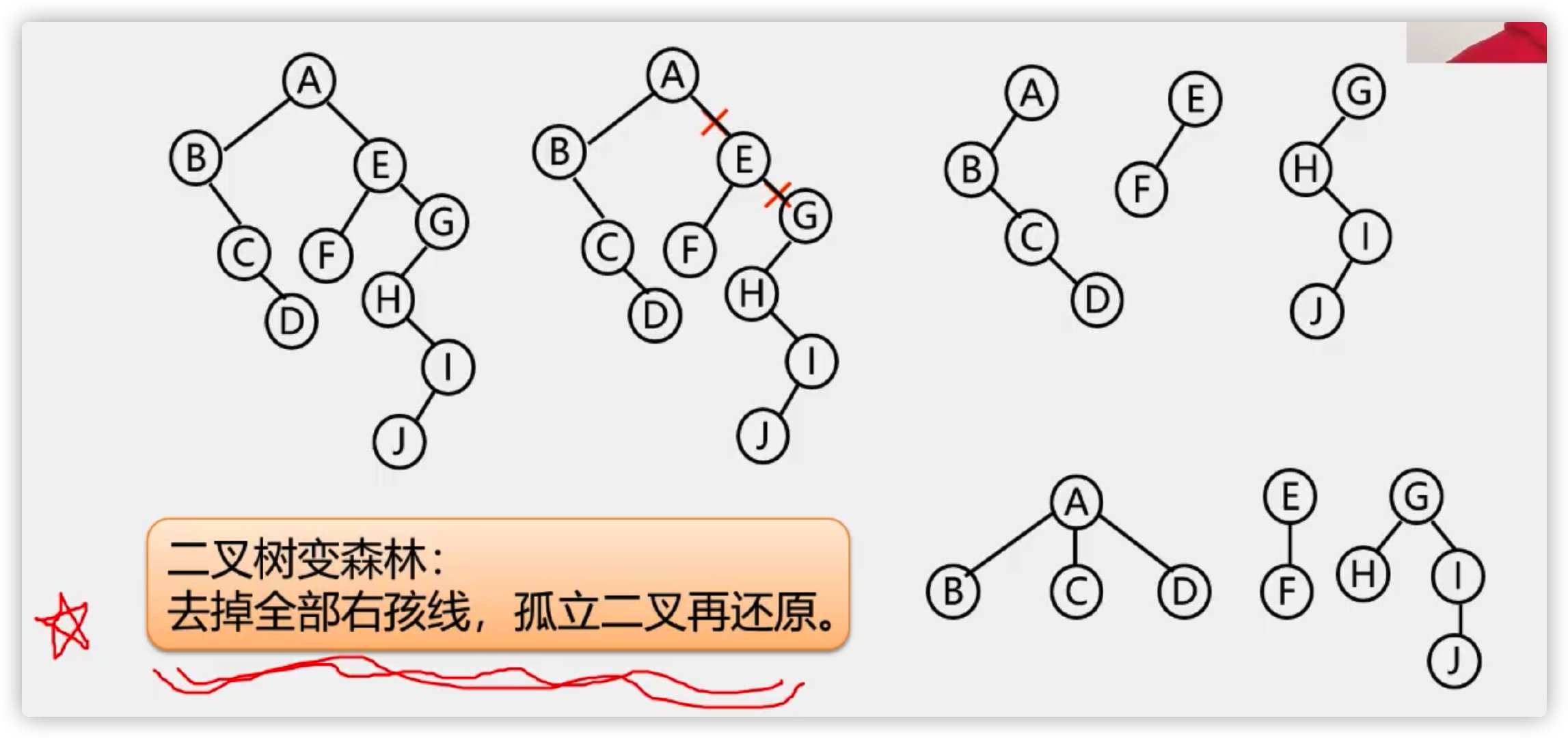
Binary tree into forest

Forest storage

First convert the forest into a binary tree, and then store the binary tree

4) Traversal of binary tree

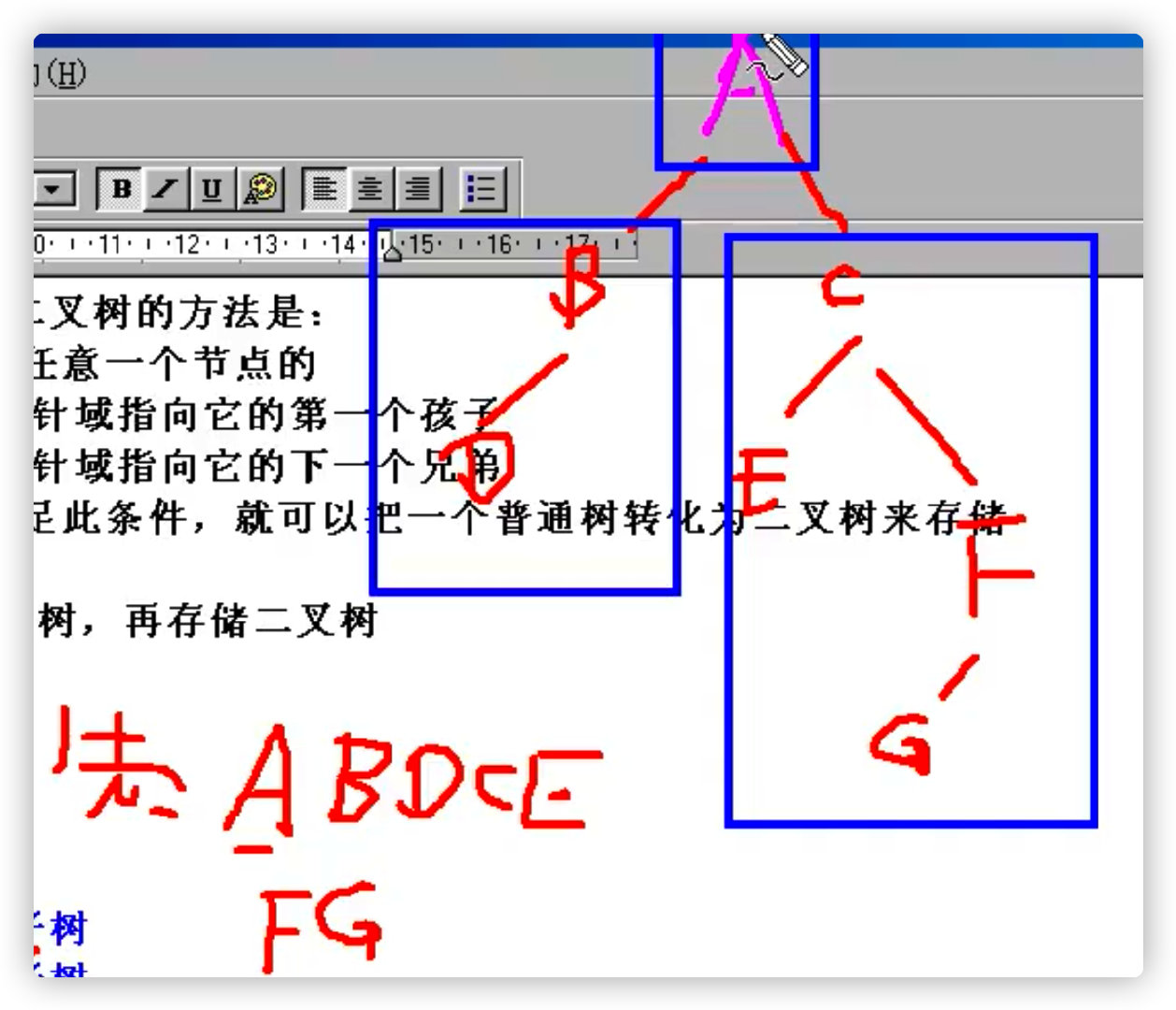
1. Preorder traversal

Access the root node first

Then access the left subtree first

Then access the right subtree first

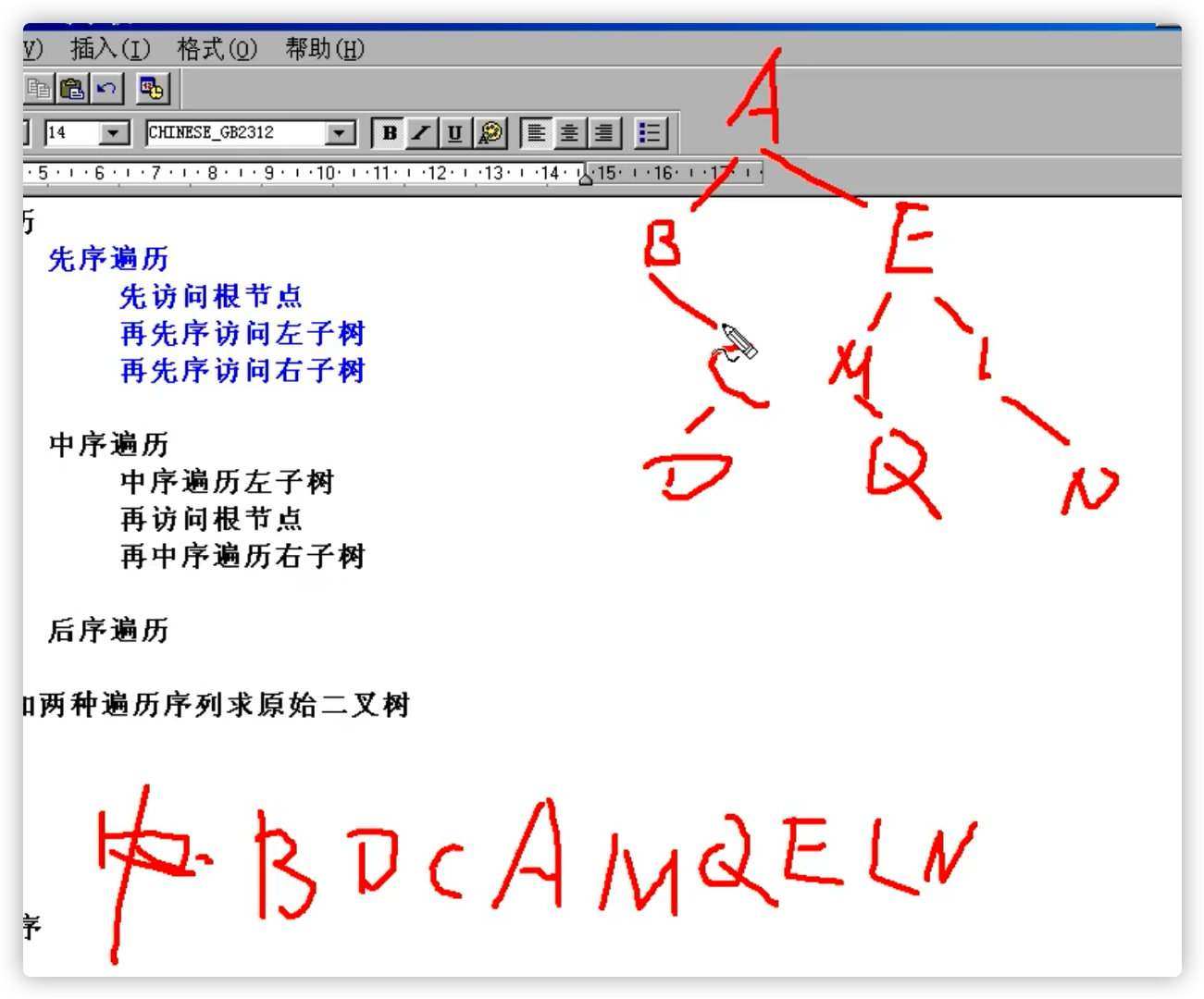
2. Medium order traversal

Middle order traversal of left subtree

Accessing the root node

Then traverse the right subtree in middle order

3. Postorder traversal

Middle order traversal of left subtree

Middle order traversal right subtree

Accessing the root node

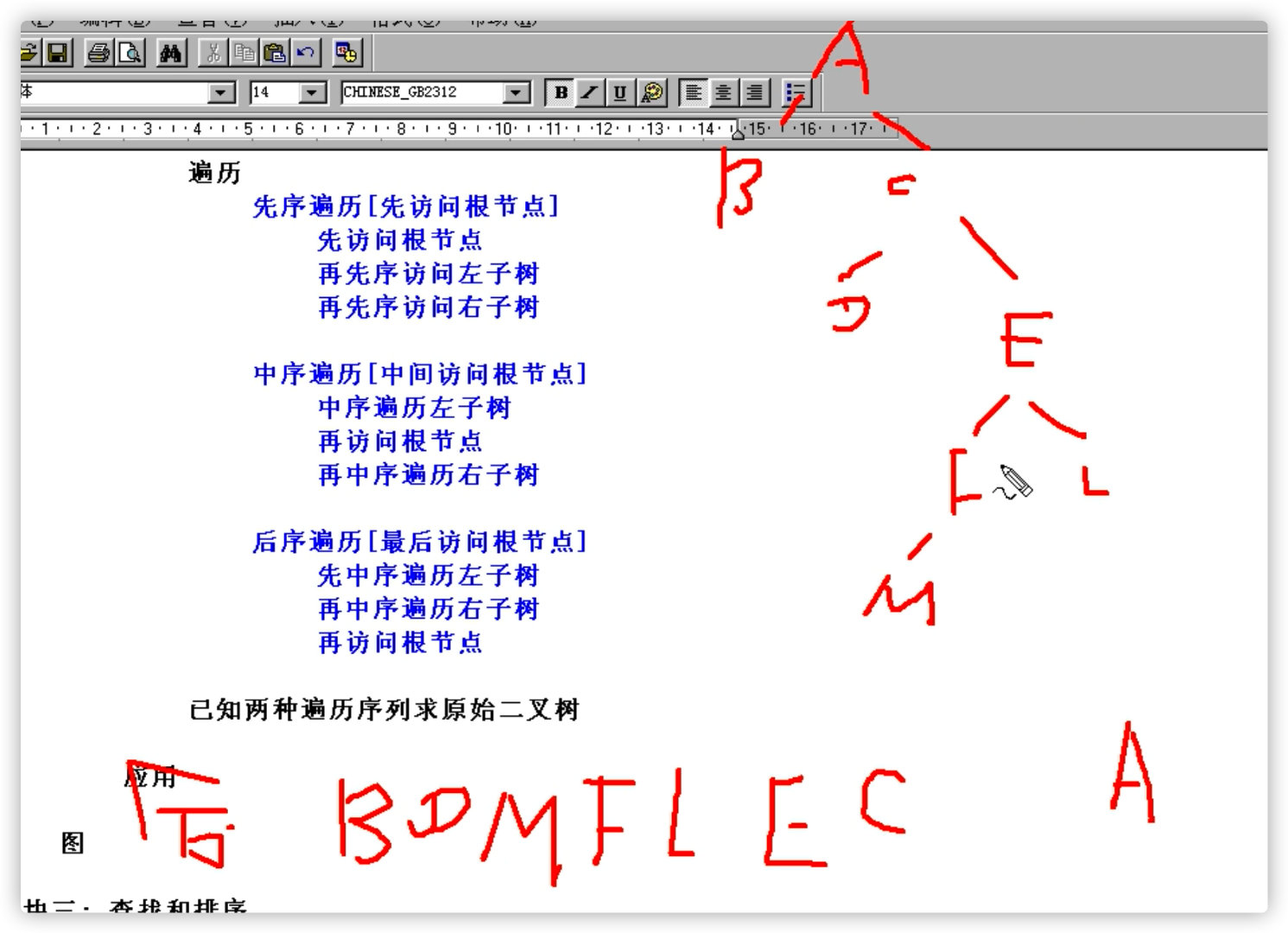
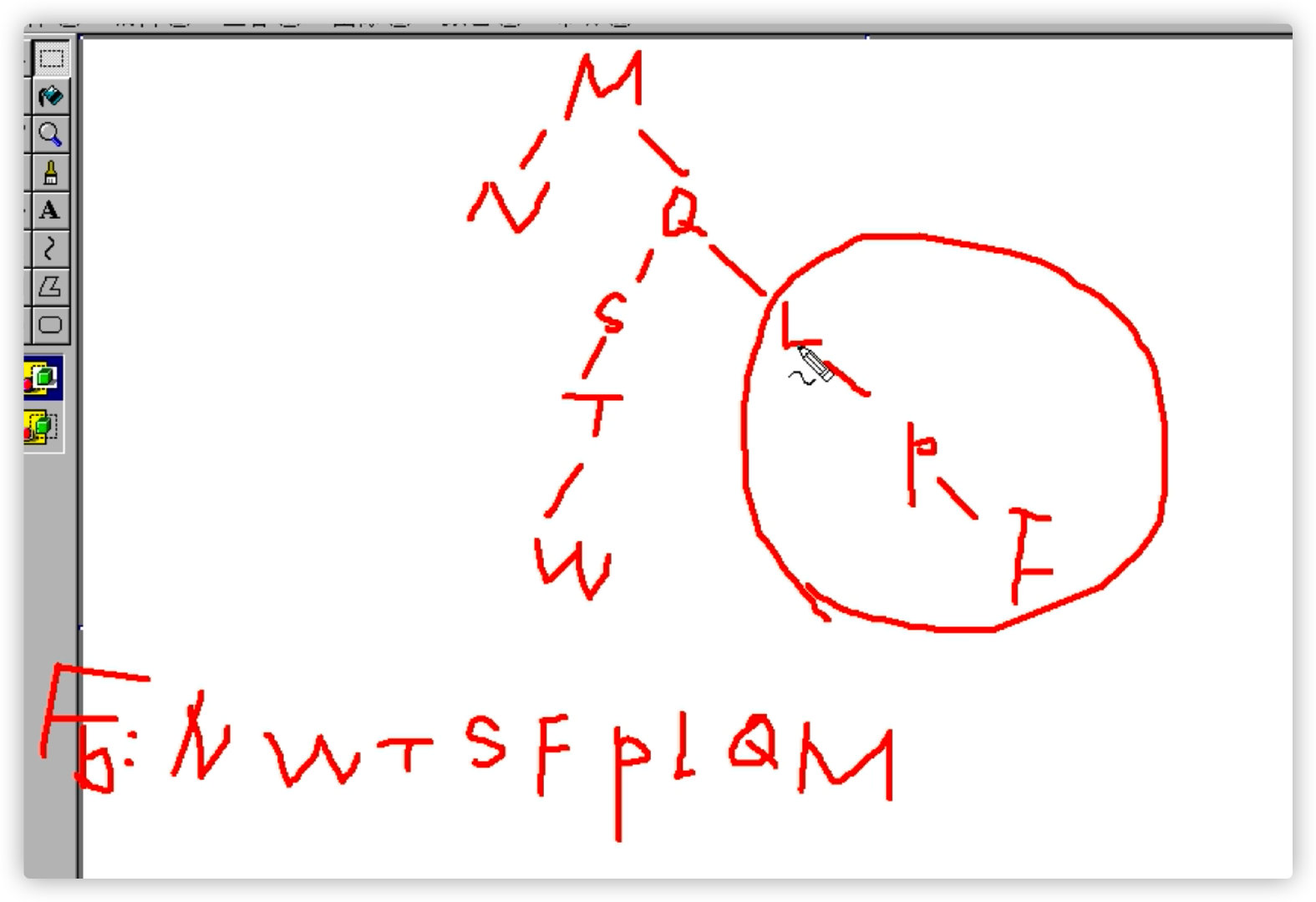
4. Two traversal sequences are known to solve the original binary tree

A binary tree can be uniquely restored by first order + middle order or middle order + subsequent

The binary tree cannot be restored through preorder + subsequent

5. Preorder + inorder -- > restore binary tree

Priority: ABCDEFGH

Middle order: BDCEAFHG

Follow up?

Example 1:

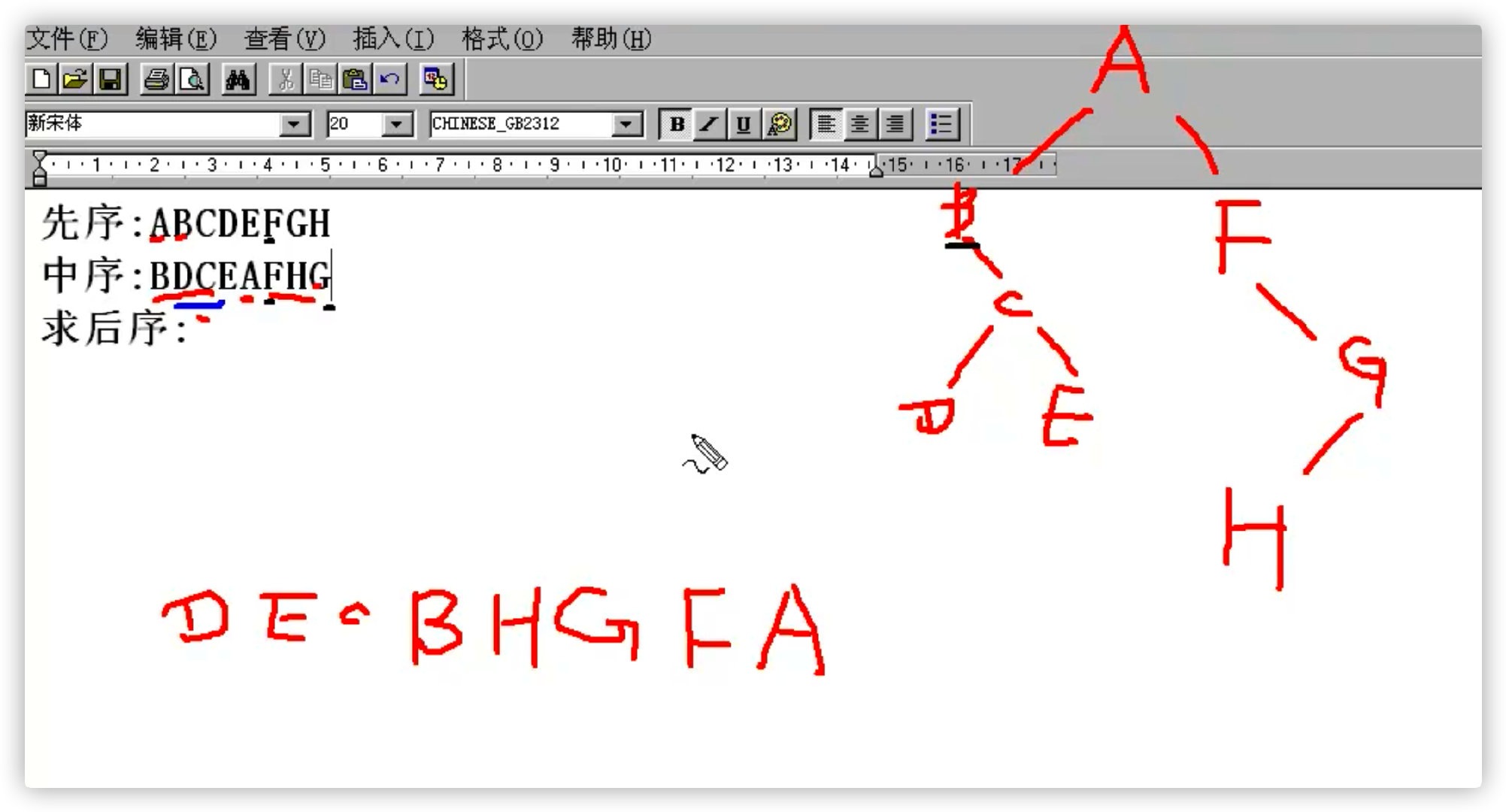
Example 2:

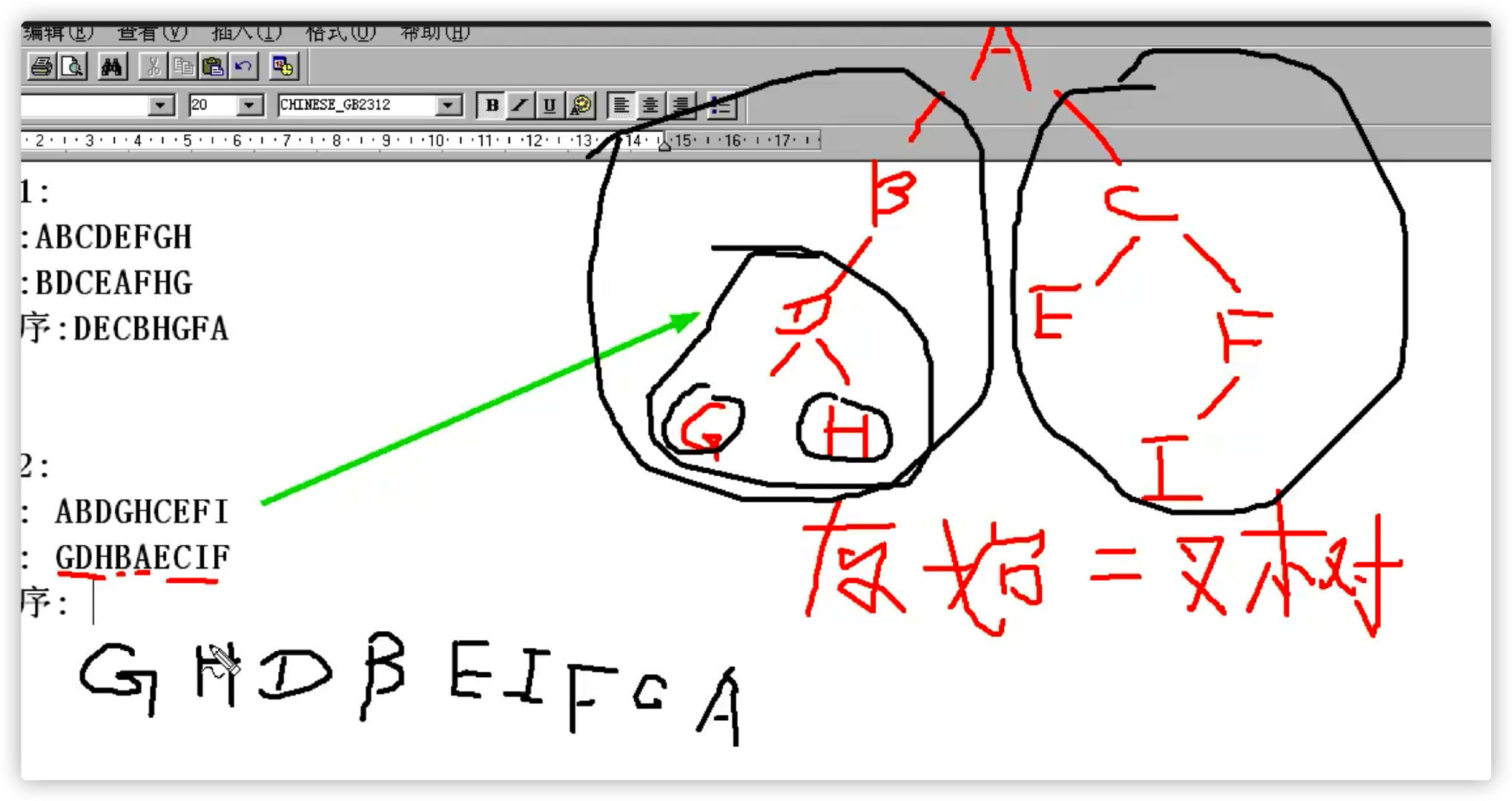
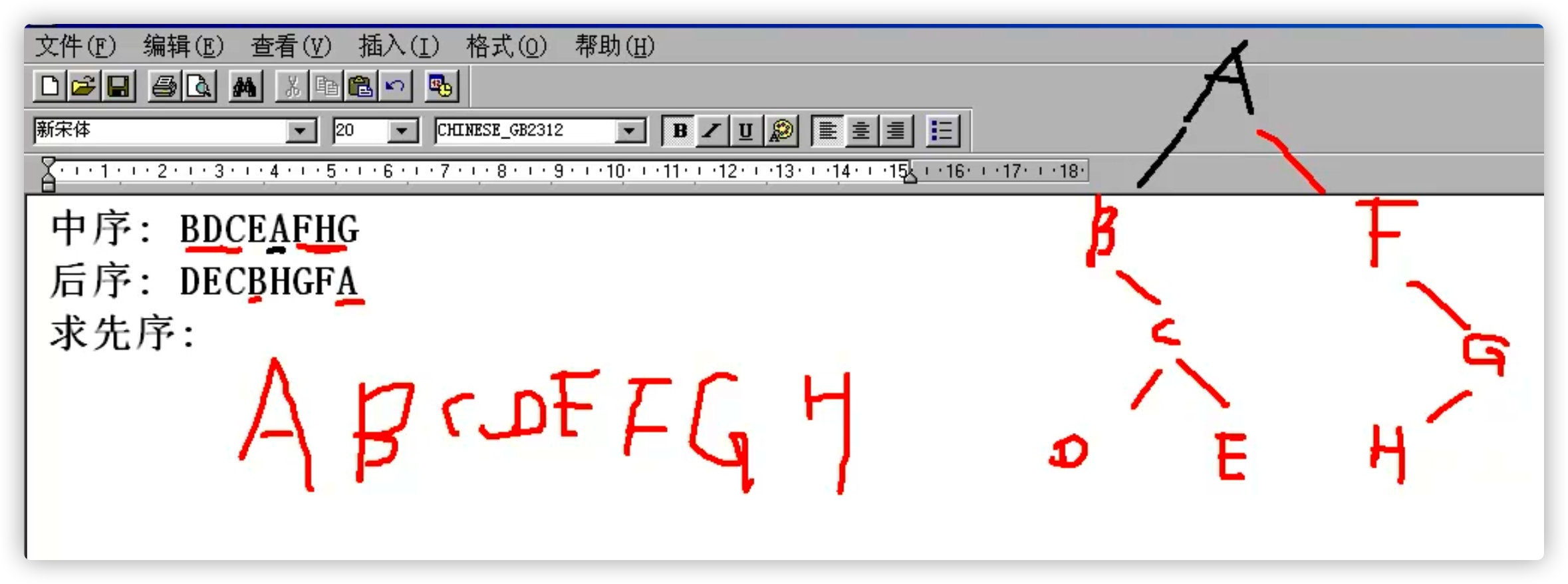
5. Middle order + post order -- > restore binary tree

Middle order: BDCEAFHG

Later: BECBHGFA

For continuation?

5) Application of and tree

1. Tree is an important form of data organization in database
2. The operating system child parent process relationship itself is a tree
3. The inheritance relationship of classes in object-oriented language is itself a tree
4. huffman tree

6) Code implementation of chain binary tree traversal

#include<stdio.h>
#include<mm_malloc.h>
struct BTNode
{
    int data;
    struct BTNode *pLchild; // p is the pointer L is the left child is the child
    struct BTNode *pRchild; // p is the pointer, R is the right child, and child is the child
};

struct BTNode * CreateBTree(){
    struct BTNode *pA = (struct BTNode *)malloc(sizeof(struct BTNode));
    struct BTNode *pB = (struct BTNode *)malloc(sizeof(struct BTNode));
    struct BTNode *pC = (struct BTNode *)malloc(sizeof(struct BTNode));
    struct BTNode *pD = (struct BTNode *)malloc(sizeof(struct BTNode));
    struct BTNode *pE = (struct BTNode *)malloc(sizeof(struct BTNode));
    pA->data = 'A';
    pB->data = 'B';
    pC->data = 'C';
    pD->data = 'D';
    pE->data = 'E';

    pA->pLchild = pB;
    pA->pRchild = pC;
    pB->pLchild = pB->pRchild =NULL;
    pC->pLchild =pD;
    pC->pRchild =NULL;
    pD->pLchild = NULL;
    pD->pRchild = pE;
    pE->pLchild = pE->pRchild = NULL;
    return pA;
}


void PreTraverseBTree(struct BTNode *pT){
    if (NULL != pT)
    {
         /*
        Pseudo algorithm
        1,First root node: pT
        2,Then start with the left subtree: Pt - > plchild represents a left subtree
        3,Right subtree first
         */
        // 1. First root node: pT
        printf("%c\n",pT->data);
        // 2. Then start with the left subtree
        if (NULL != pT->pLchild)
        {
            PreTraverseBTree(pT->pLchild);
        }
        
        // 3. Right subtree first
        if (NULL != pT->pRchild)
        {
            PreTraverseBTree(pT->pRchild);
        }
    }
    
    

}

void InTraverseBTree(struct BTNode *pT){
    if (NULL != pT)
    {
        //1. First order traversal of left subtree
        if (NULL != pT->pLchild)
        {
            InTraverseBTree(pT->pLchild);
        }
        
        //2. Access root node
        printf("%c\n",pT->data);

        //3. Middle order traversal right subtree
        if (NULL != pT->pRchild)
        {
            InTraverseBTree(pT->pRchild);
        }
    }
    
}

void PostTraverseBTree(struct BTNode *pT){
  if (NULL != pT)
    {
        //1. First order traversal of left subtree
        if (NULL != pT->pLchild)
        {
            PostTraverseBTree(pT->pLchild);
        }
        //2. Middle order traversal right subtree
        if (NULL != pT->pRchild)
        {
            PostTraverseBTree(pT->pRchild);
        }
        //3. Access root node
        printf("%c\n",pT->data);
    }
}

int main(){

    struct BTNode *pT = CreateBTree(); // Create binary tree
    // The non-linear call can only be output when it is converted to linear, and it can be output in sequential mode
    // PreTraverseBTree(pT); 
    // InTraverseBTree(pT); 
    PostTraverseBTree(pT); 

    return 0;
}

7) Application of binary tree traversal algorithm

Duplicate binary tree

Depth of computer binary tree

Calculate the total number of nodes in the binary tree

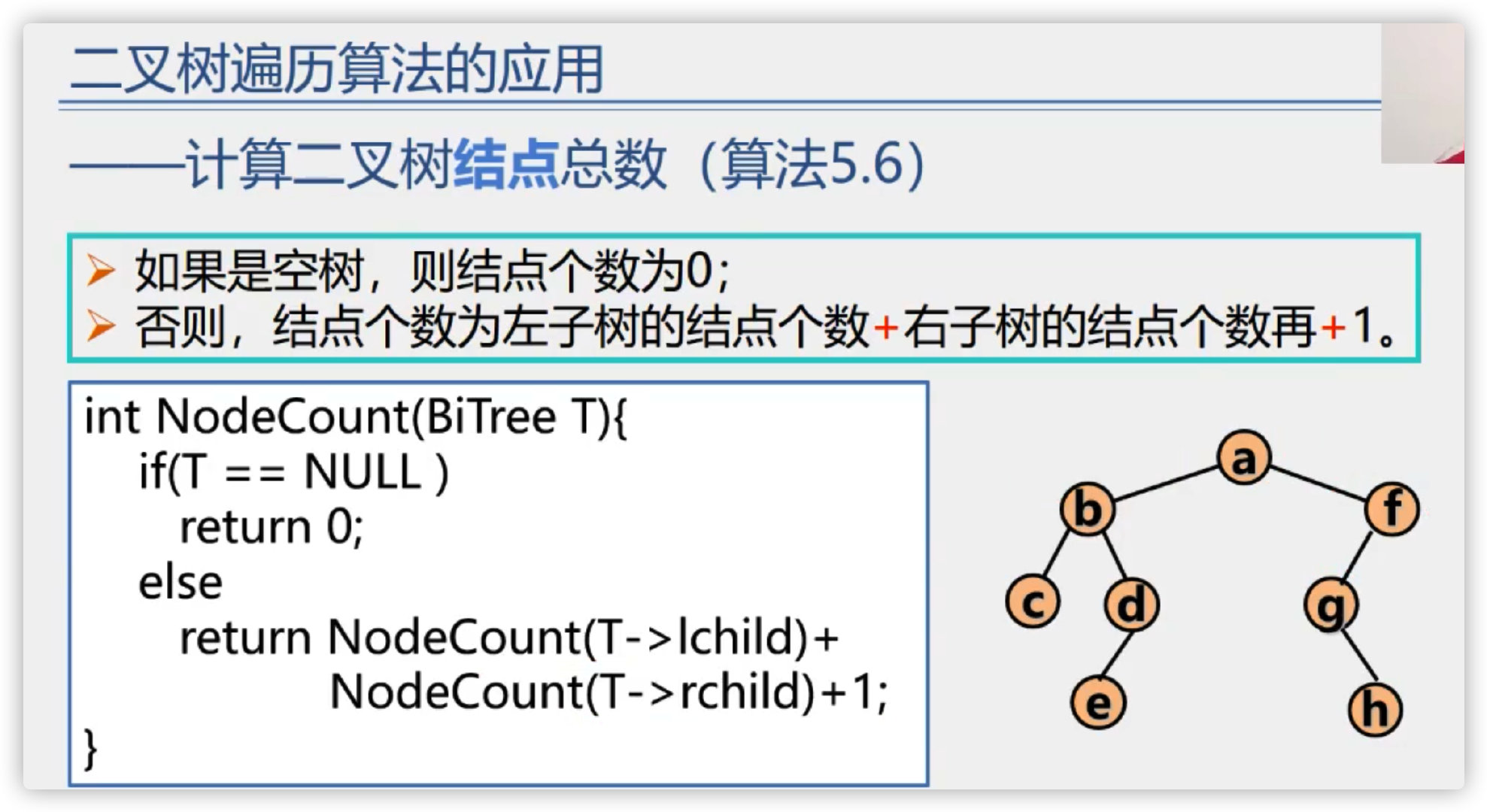
Calculate the total number of leaf nodes of binary tree

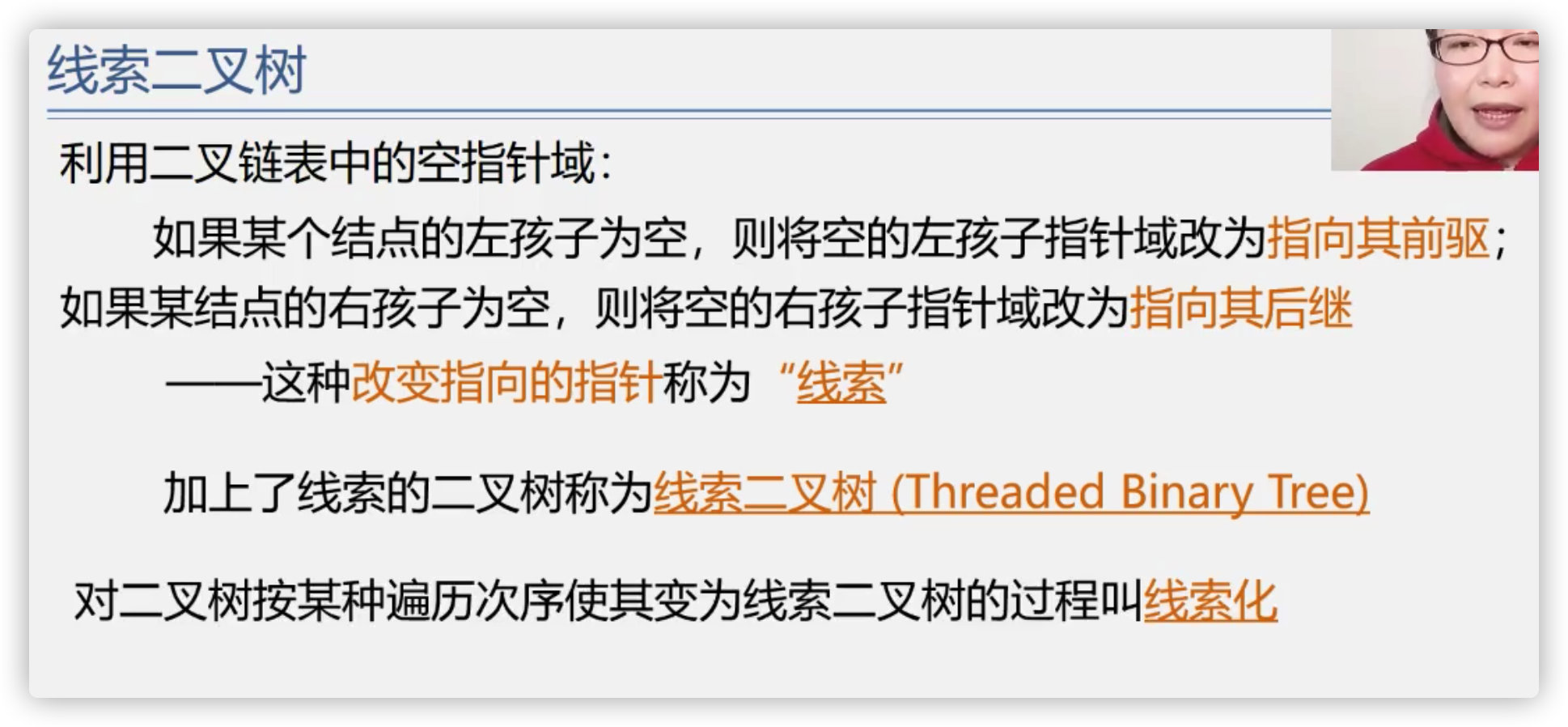
8) Clue binary tree

(1) . definition

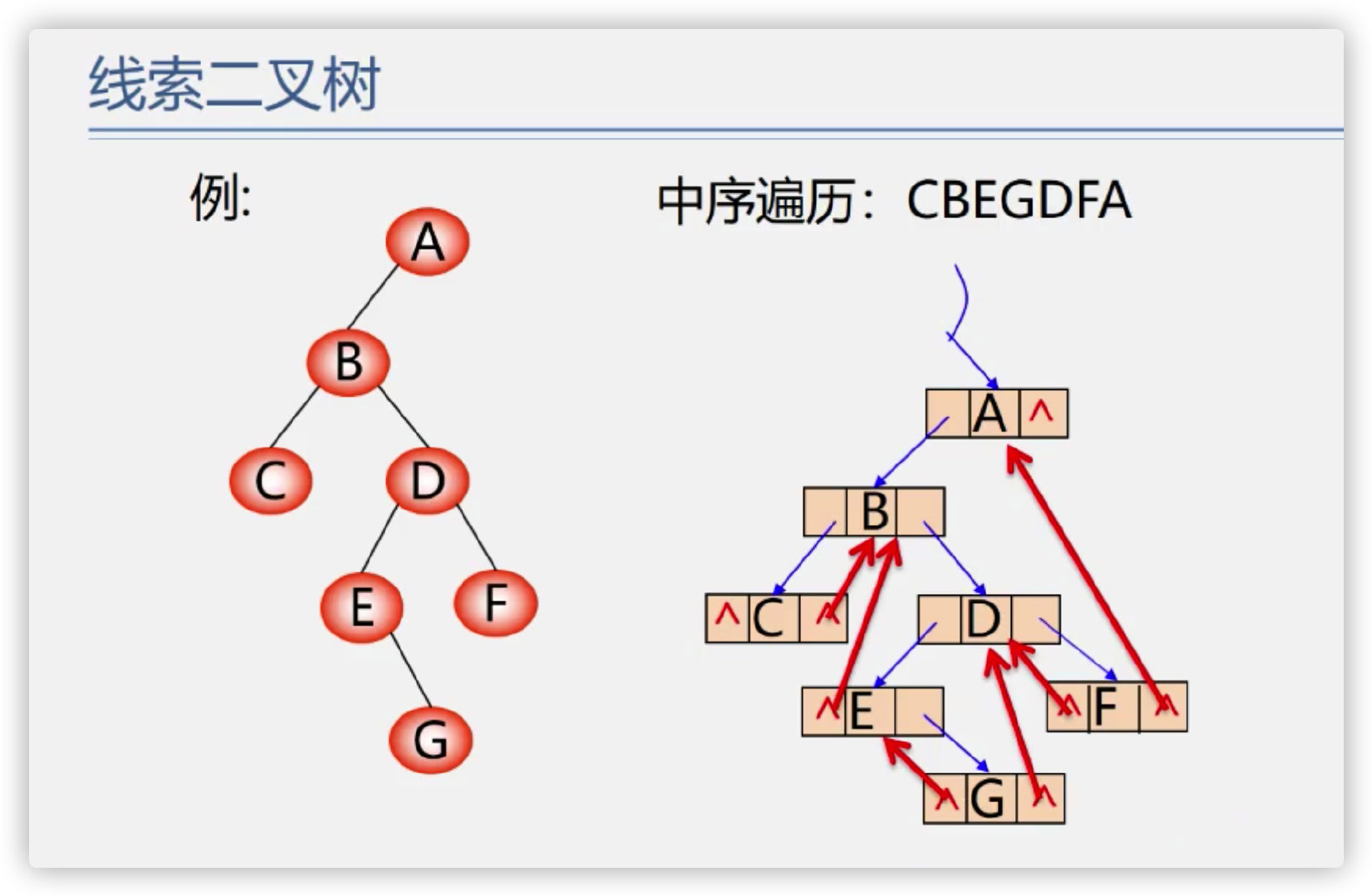
(2) . case demonstration

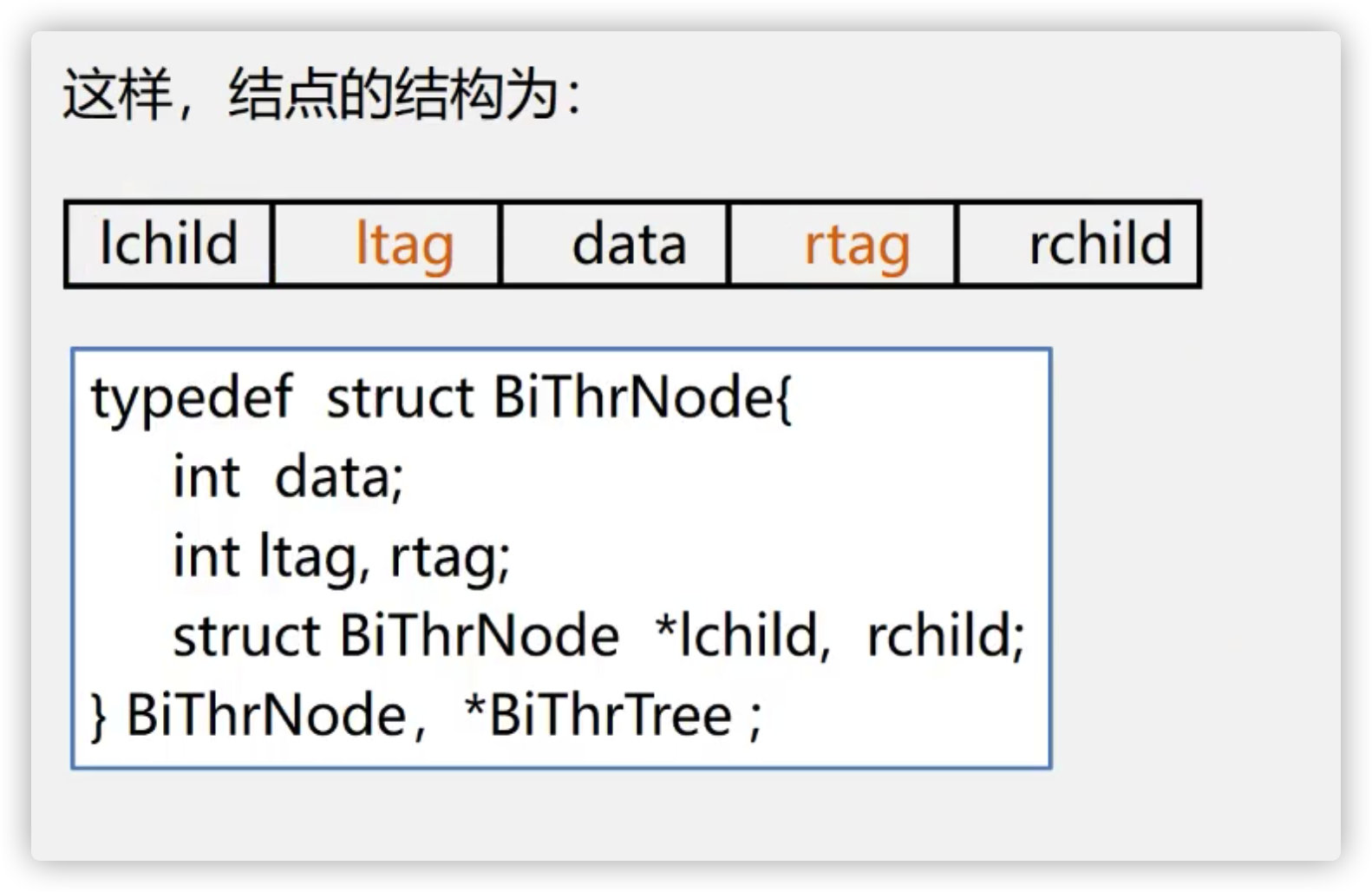
(3) . flag field

Exercises

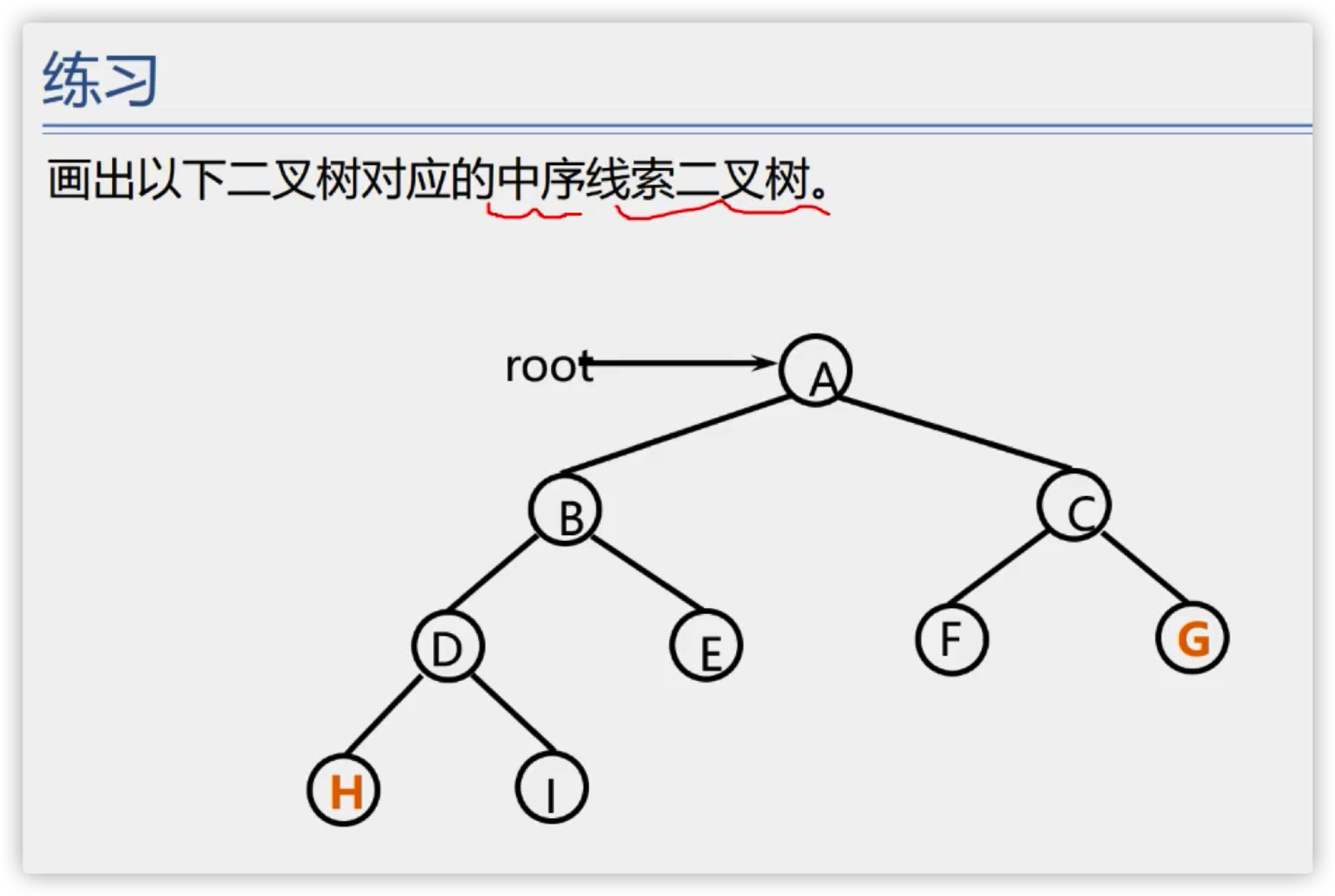
To solve the problem of pointing to null, a header node is added

9) , Huffman tree

Introduction

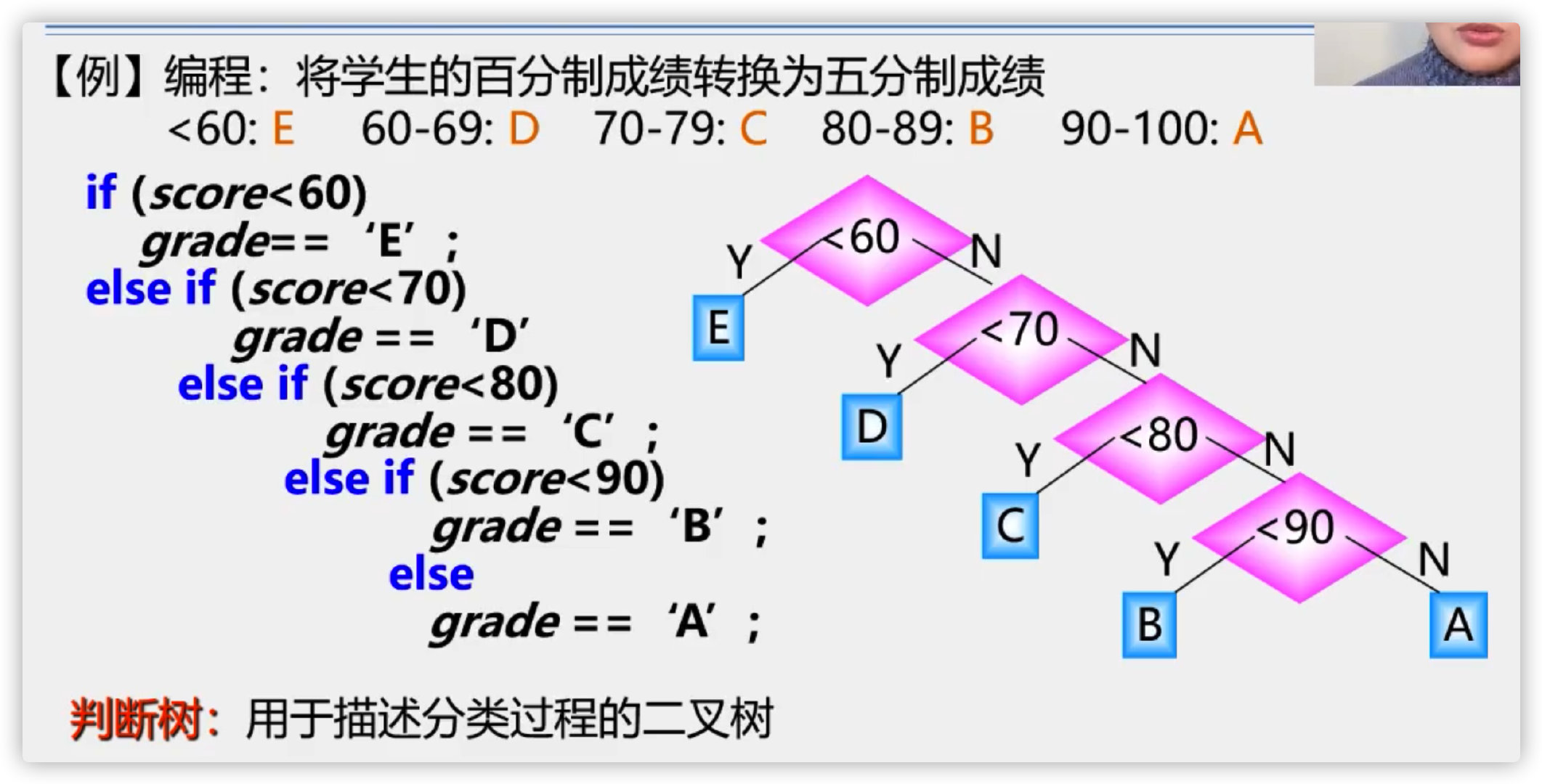
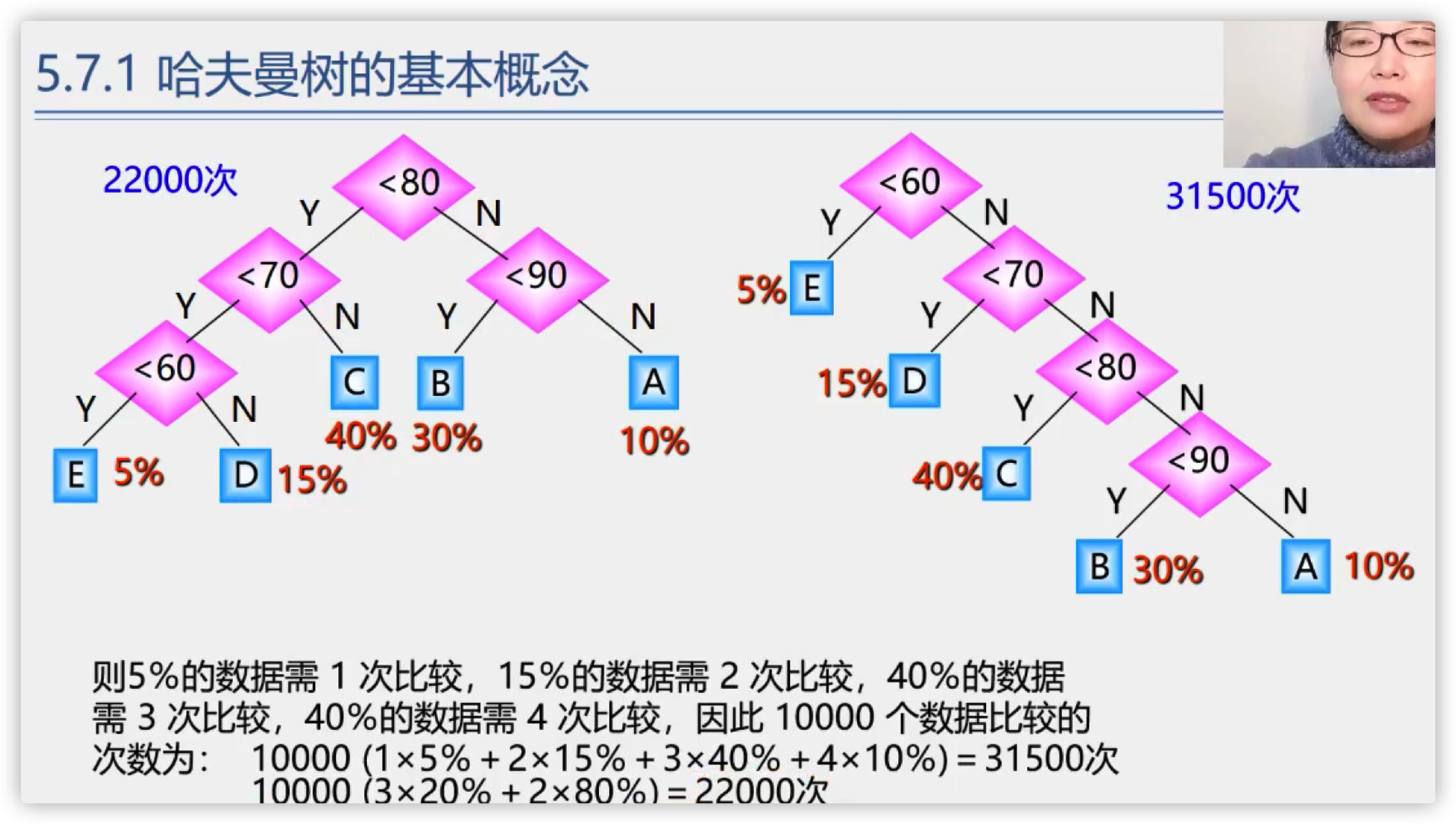
(1) Basic concepts

route

Path length of node

[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (img-w5cpy8cy-1636095678842) (/ users / ouyangyansong / library / Application Support / typera user images / image-20211104205500558. PNG)]

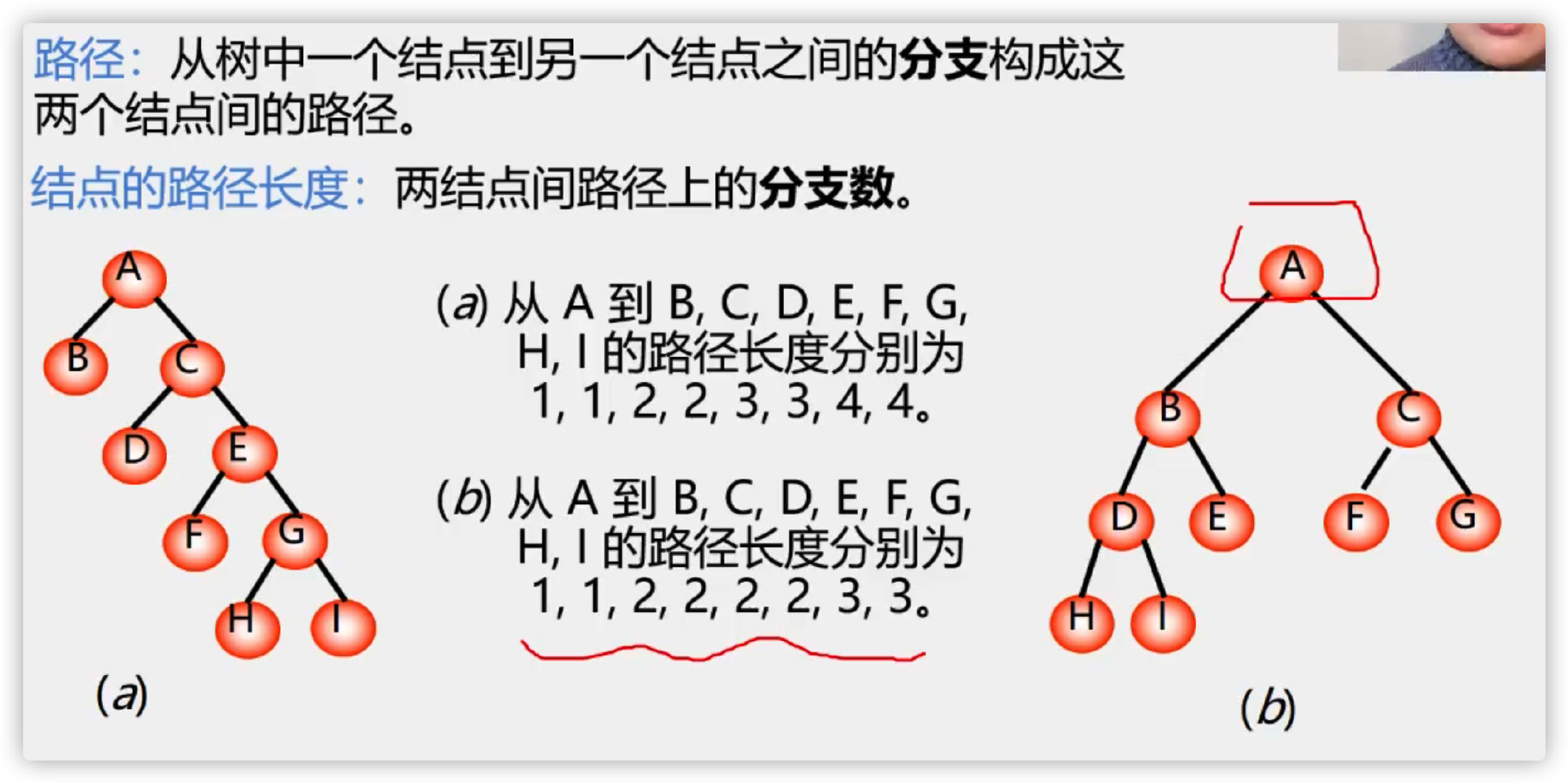
Path length of tree

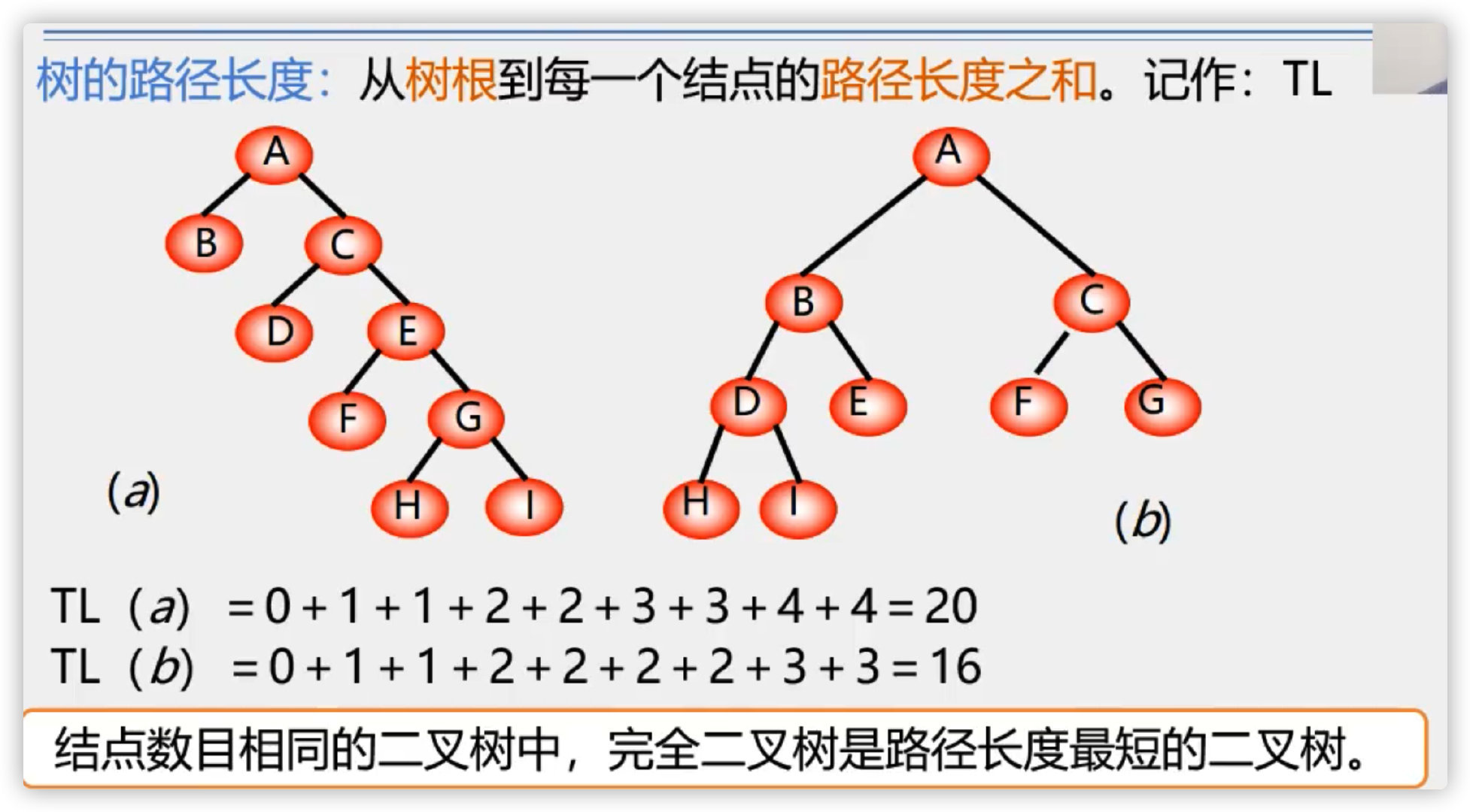
Note: complete binary tree is not necessarily the shortest path, and incomplete binary tree can also be the shortest path

Weight

Weighted path length of node

Weighted path length of tree

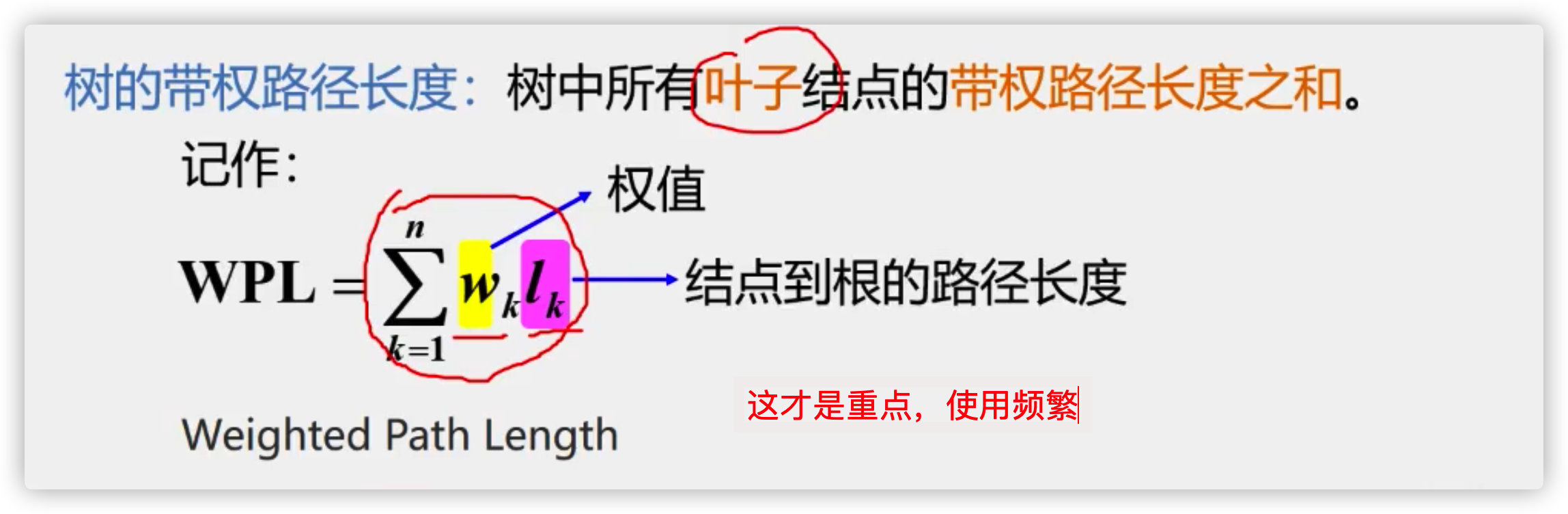
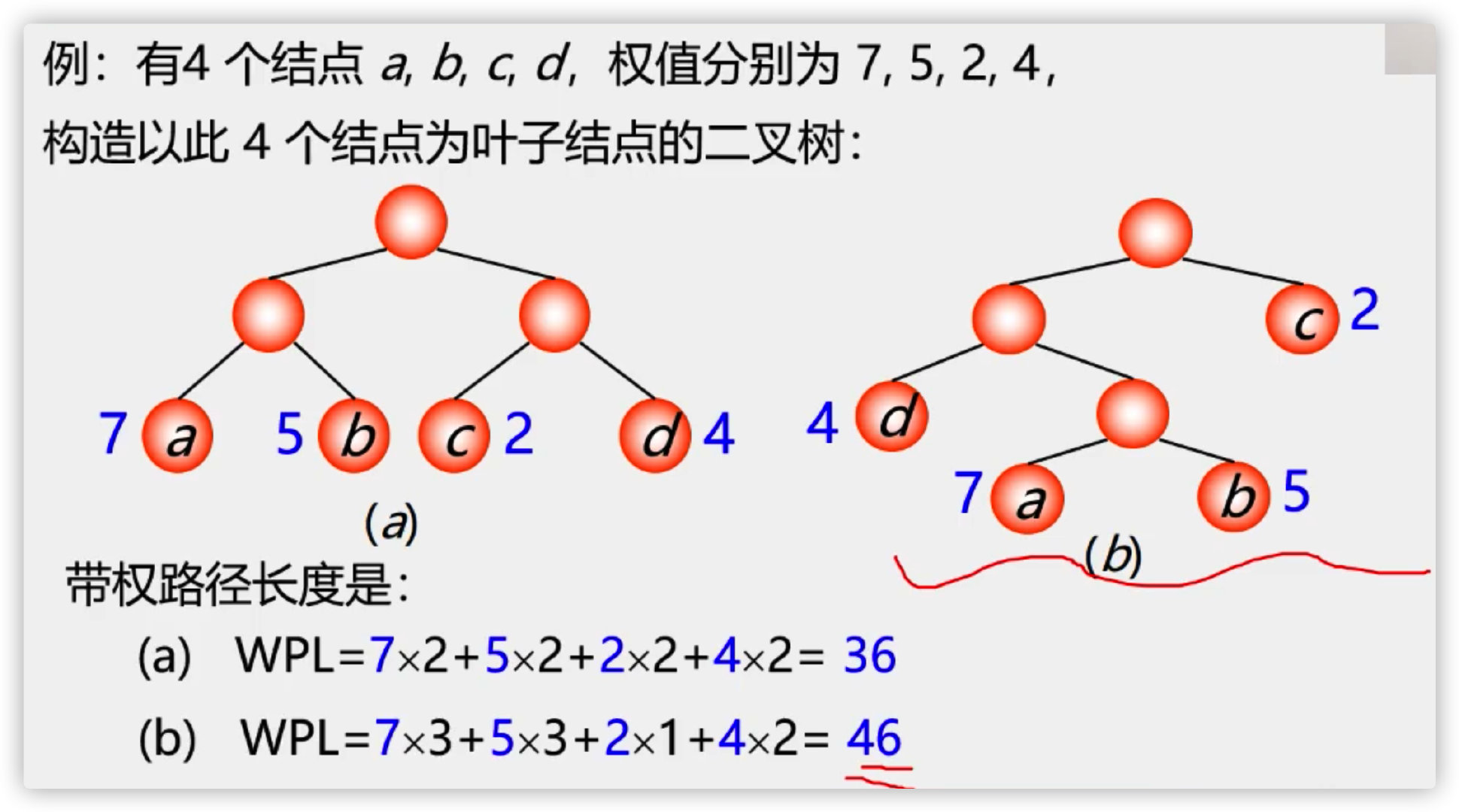
Calculation of weighted binary tree

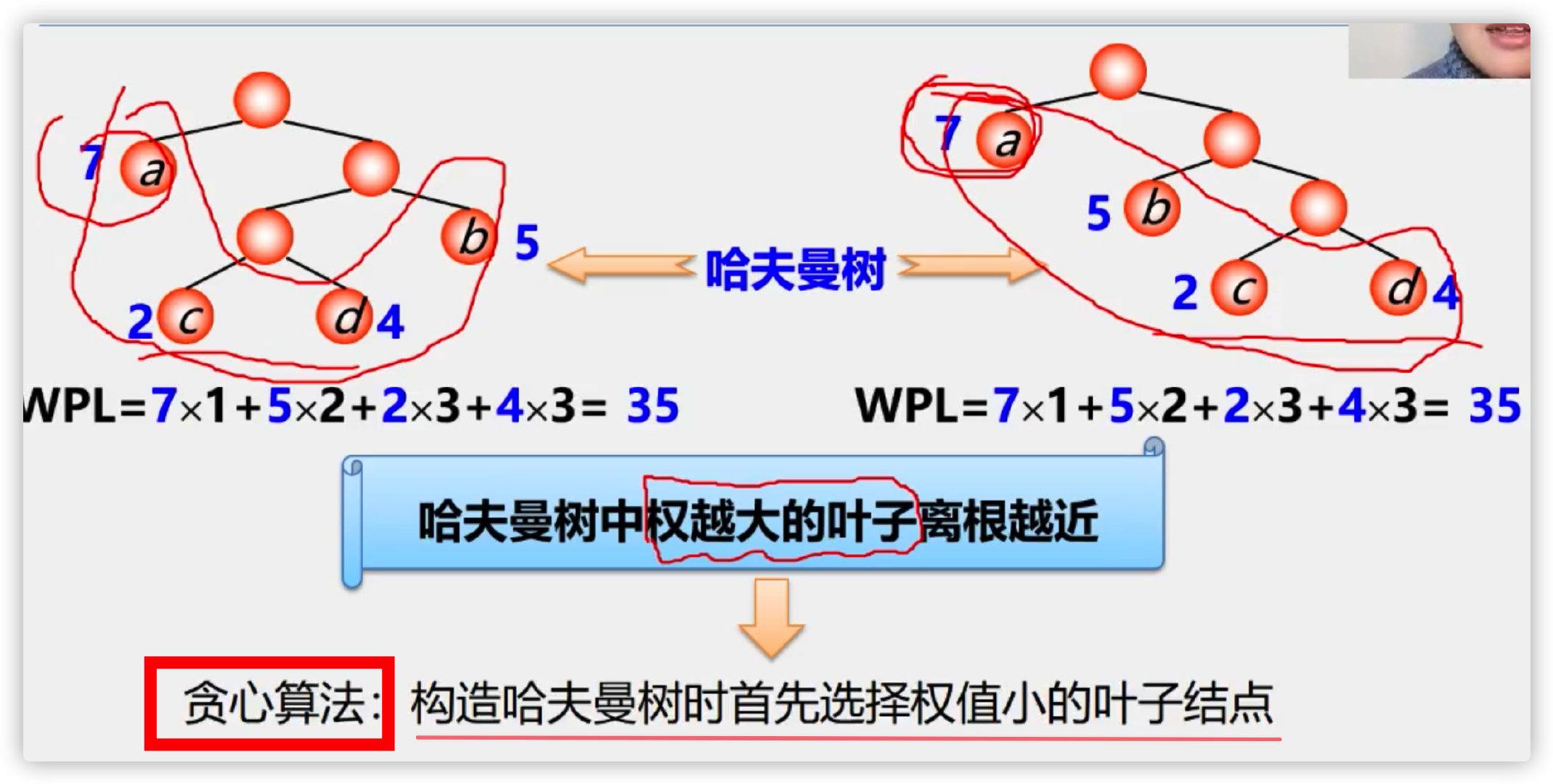
(2) Definition

Conclusion:

1. A full binary tree is not necessarily a Huffman tree

2. Huffman trees with the same weighted nodes are not unique

(3) Constructing Huffman tree

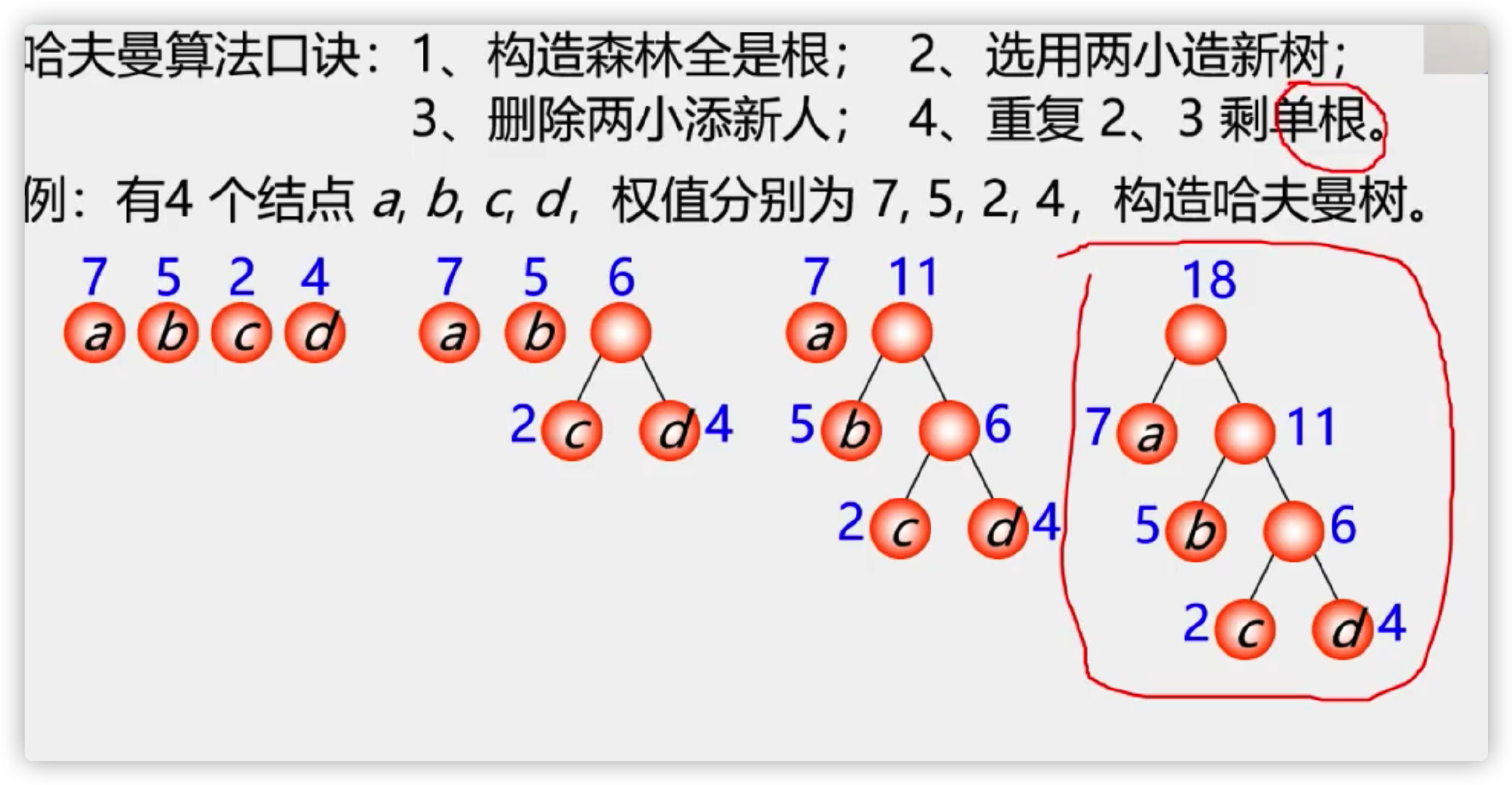
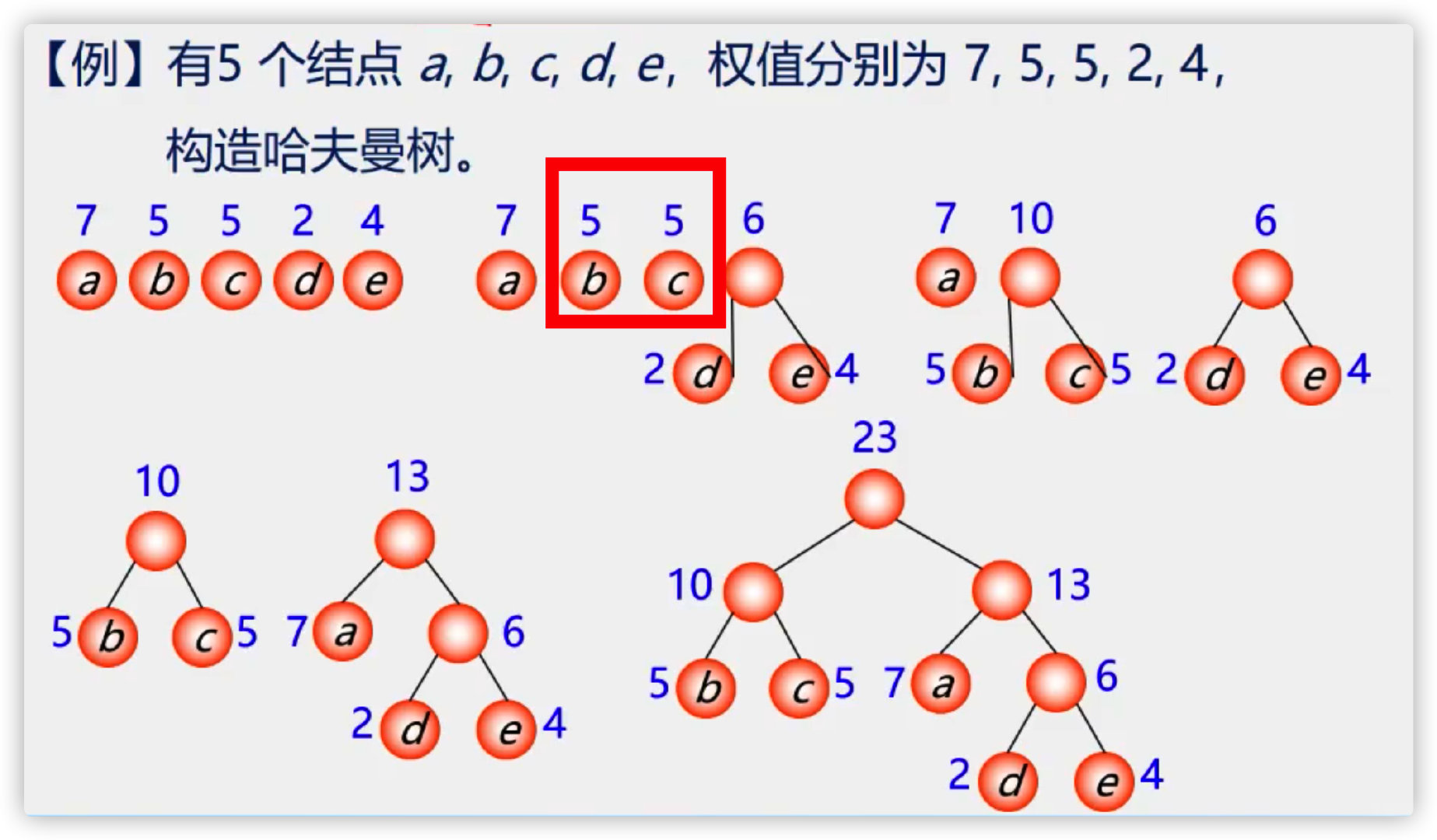
(4) Implementation of Huffman tree algorithm

Using sequential storage structure - one-dimensional structure array

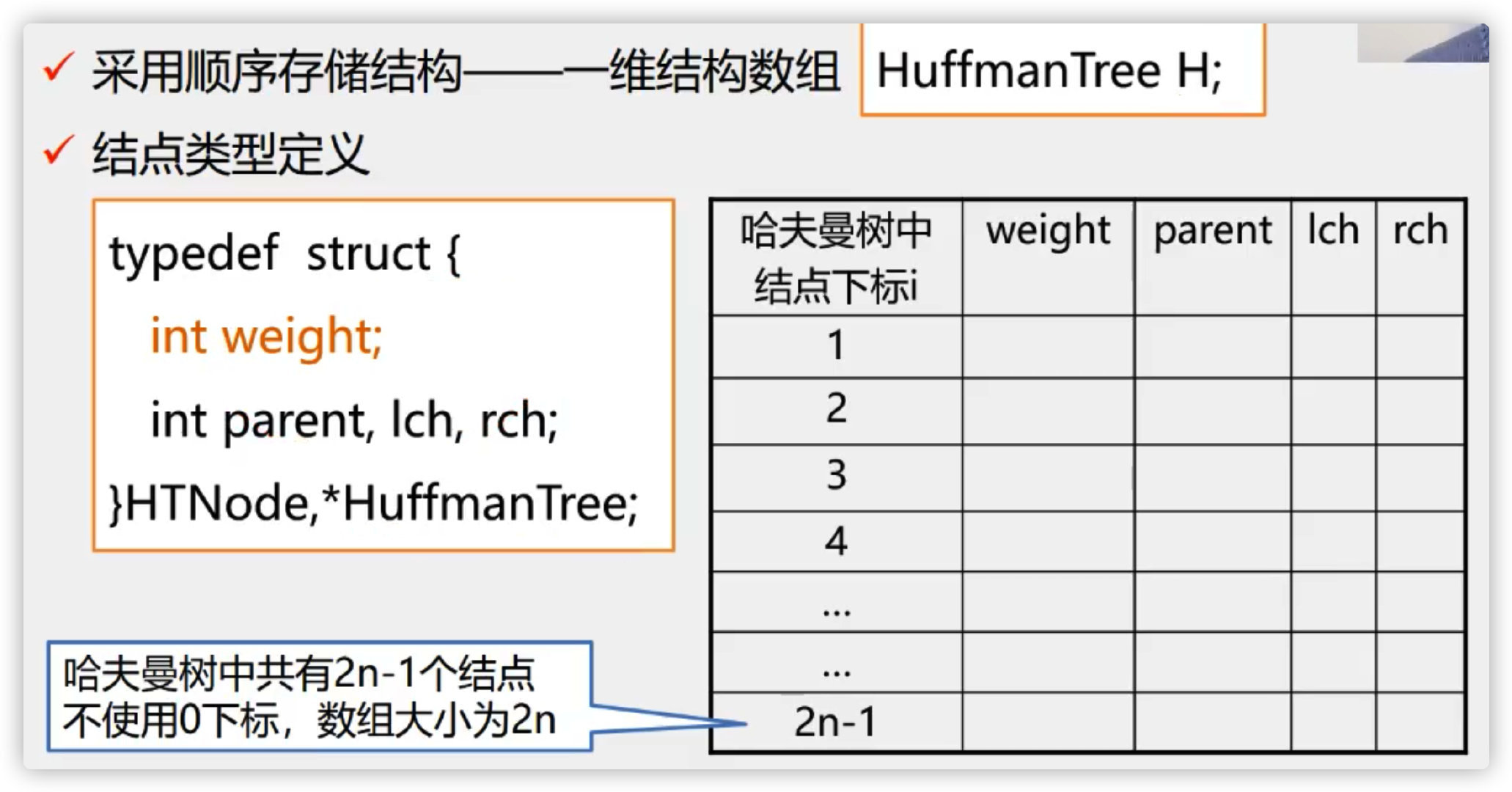
initialization

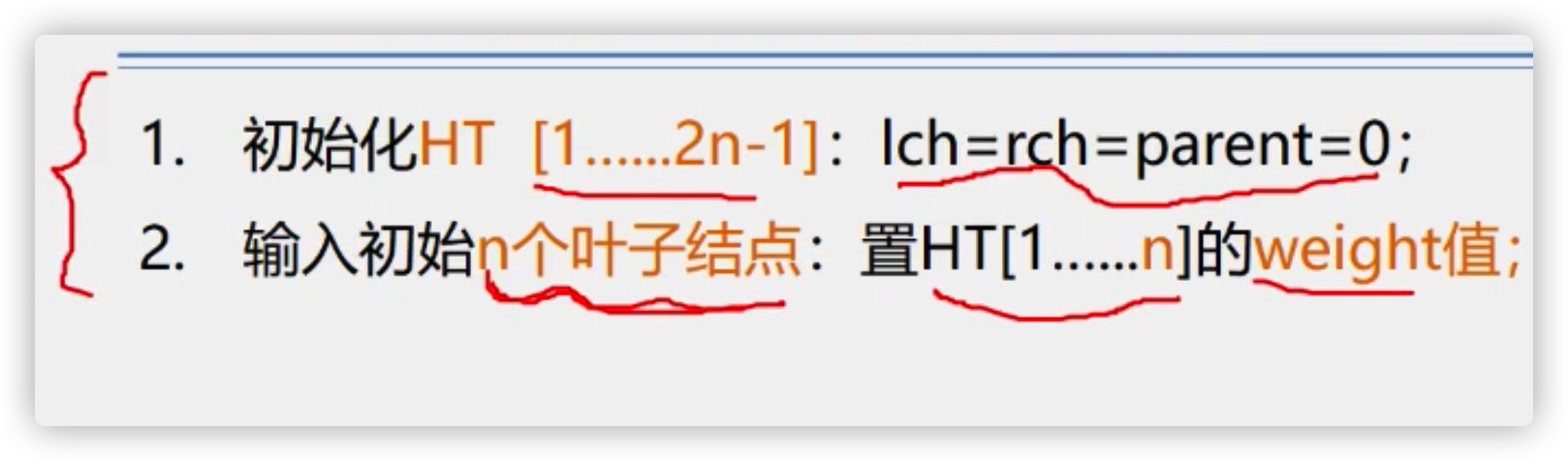
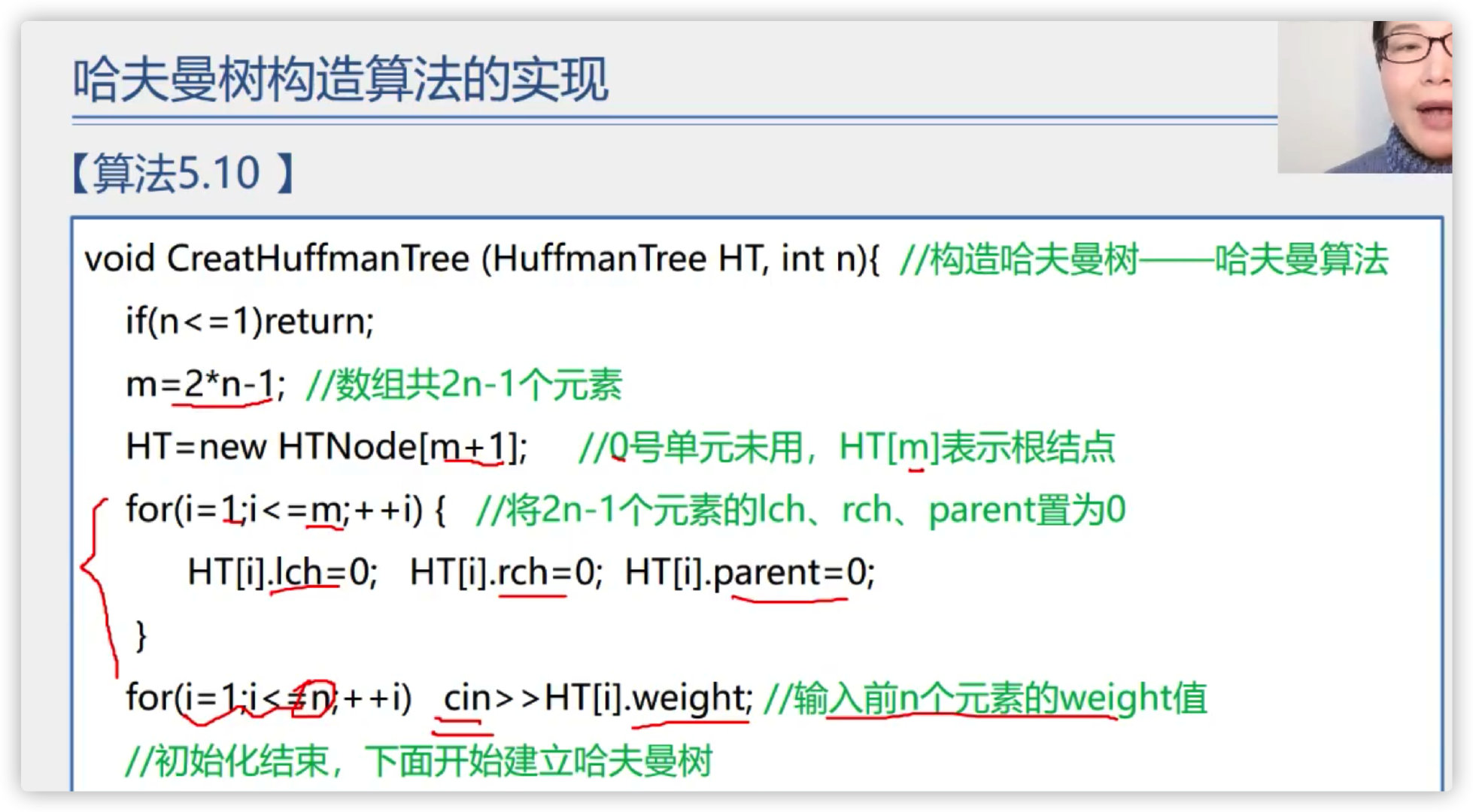
Merge to generate a new node

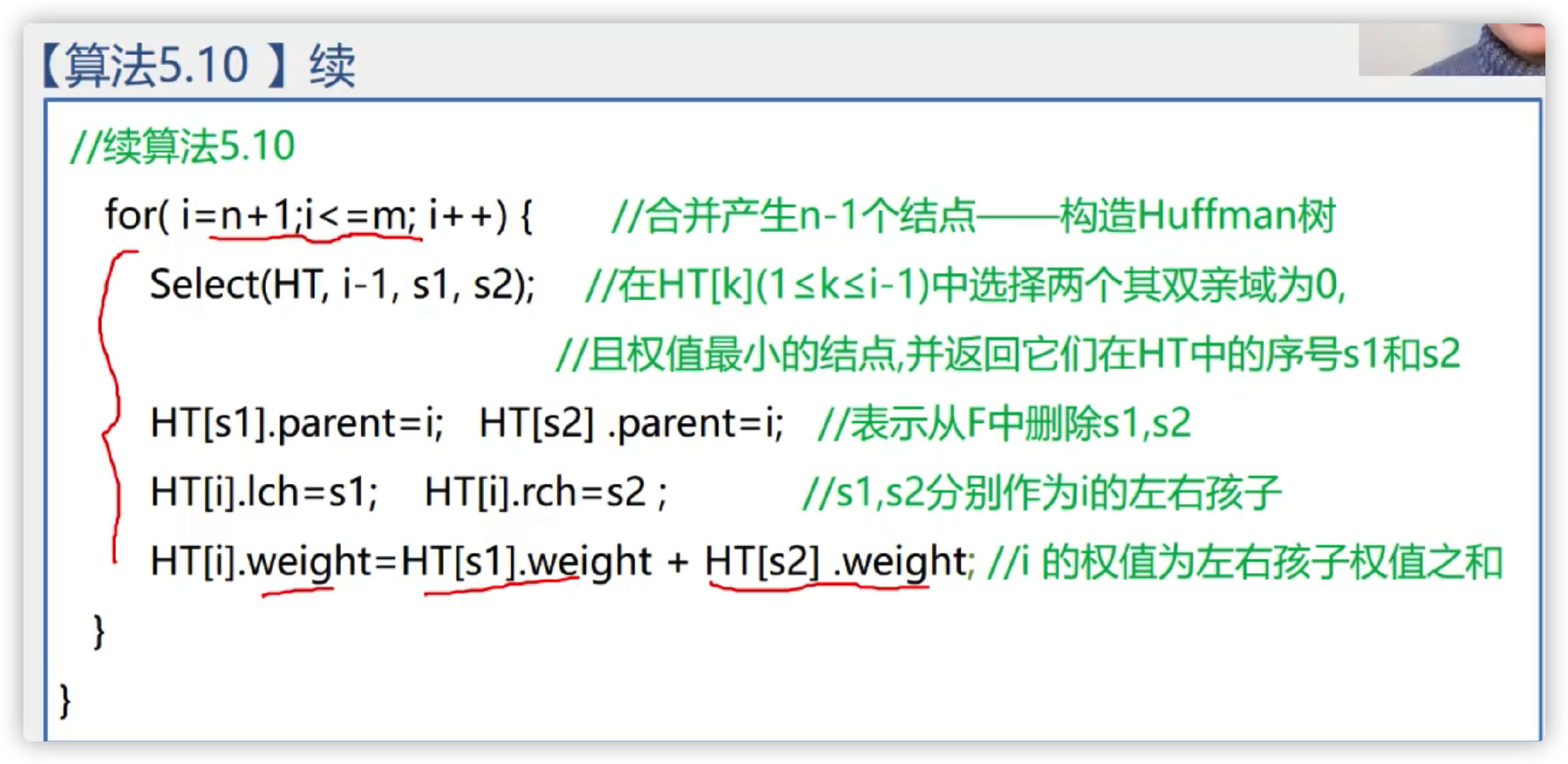
example

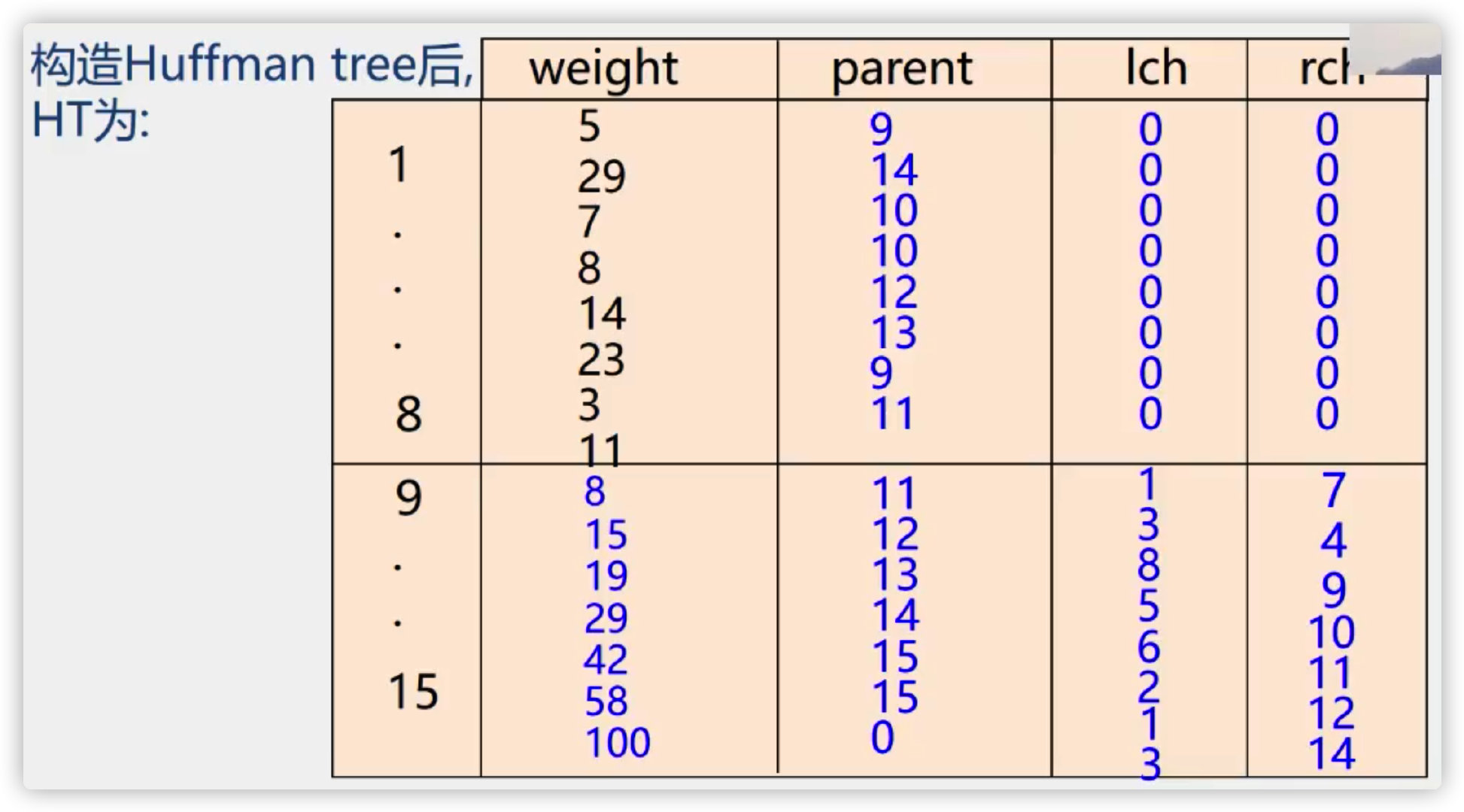
(5) Huffman coding

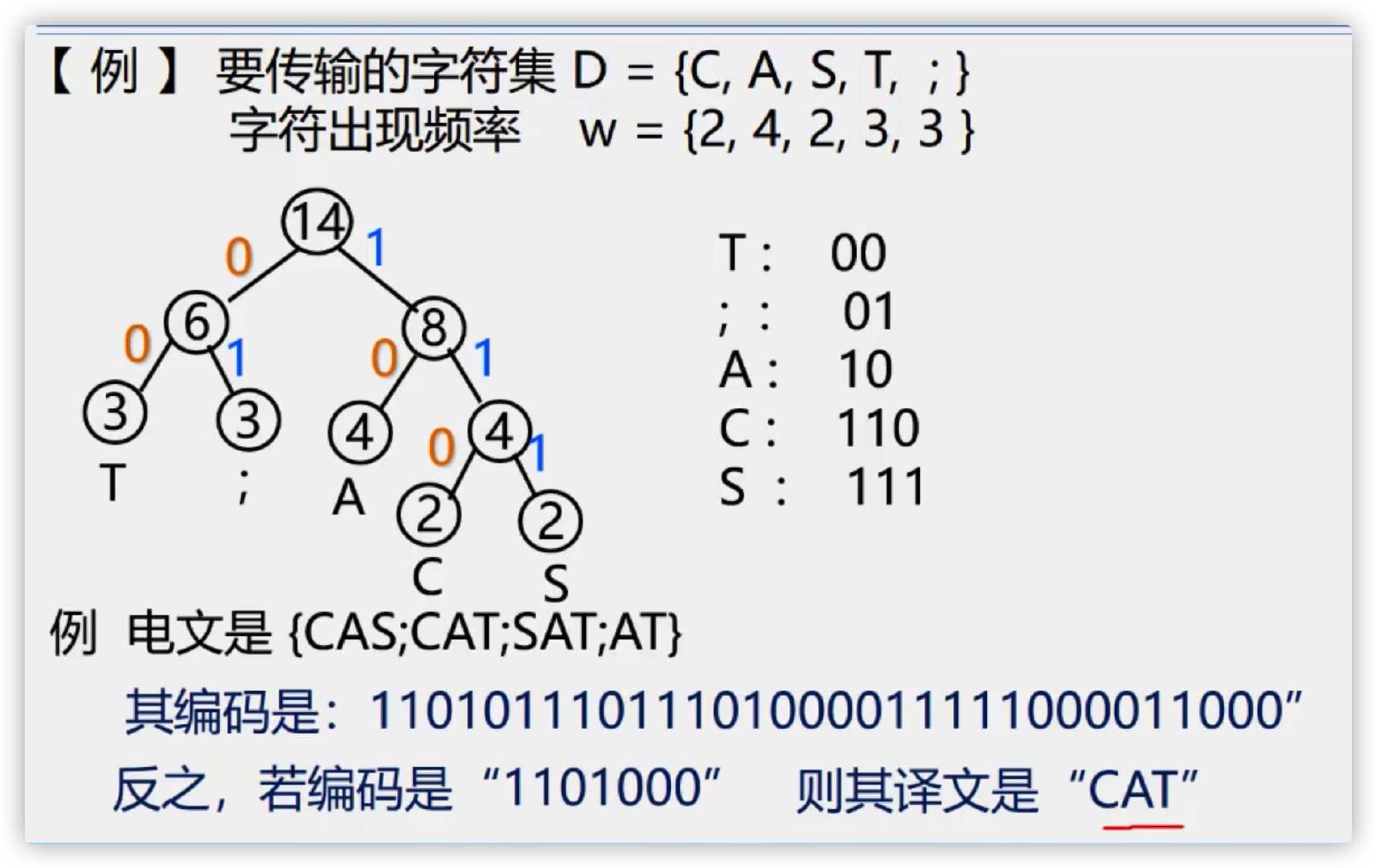
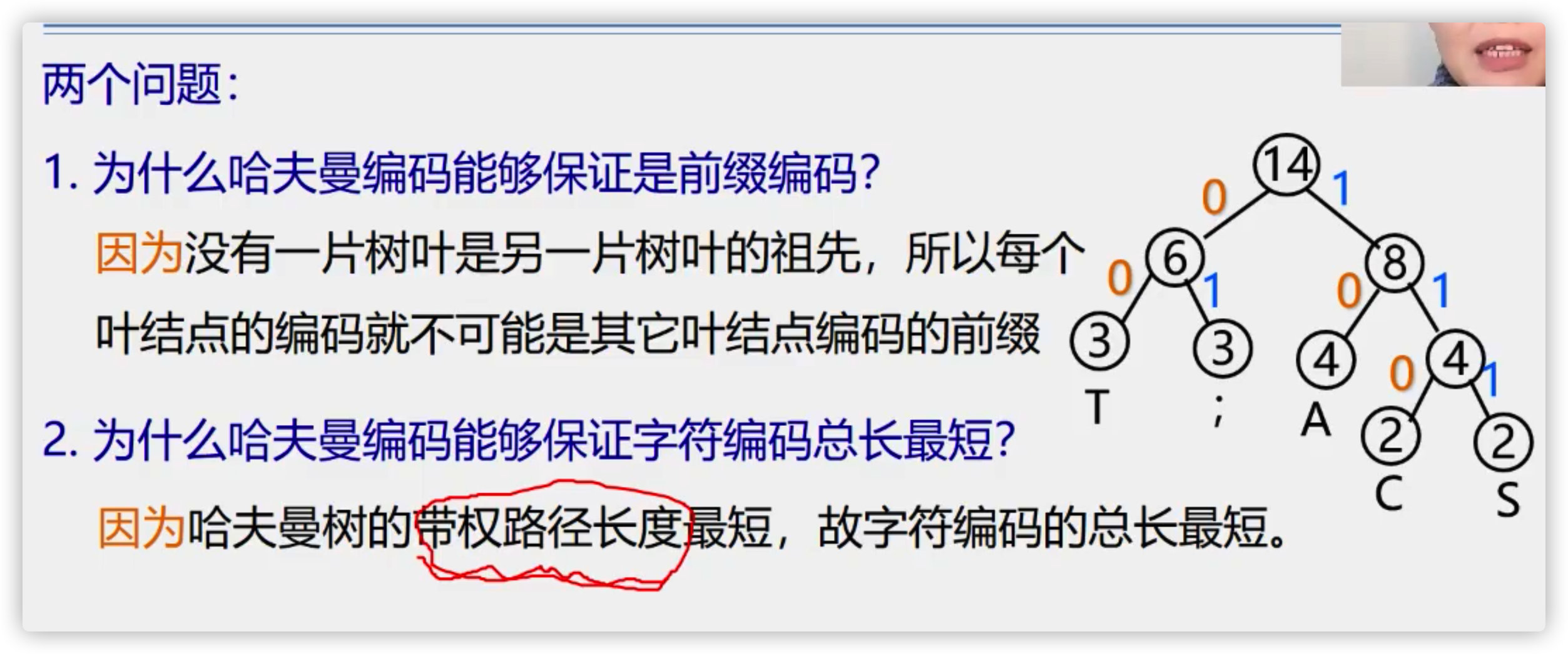
Examples

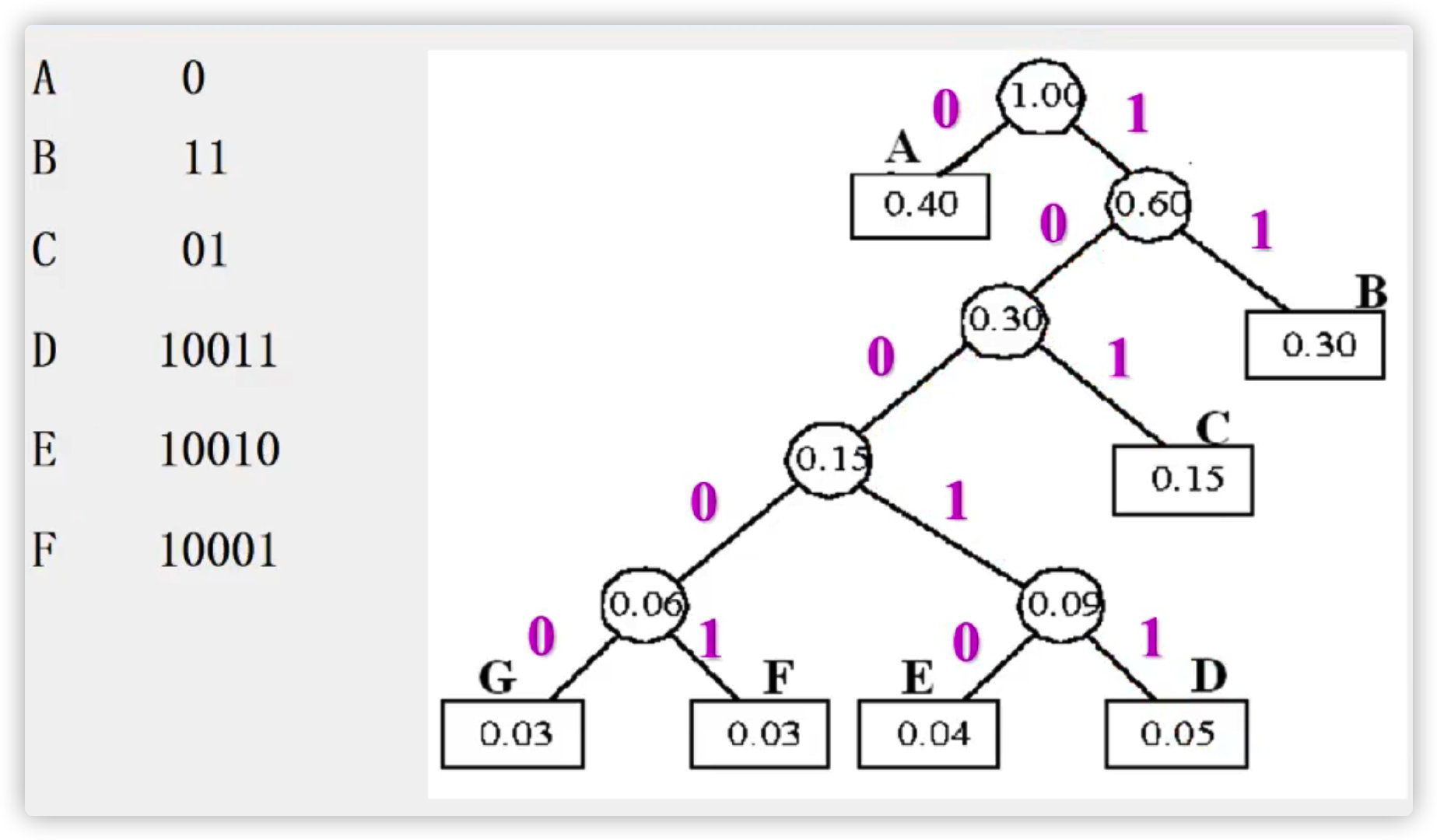
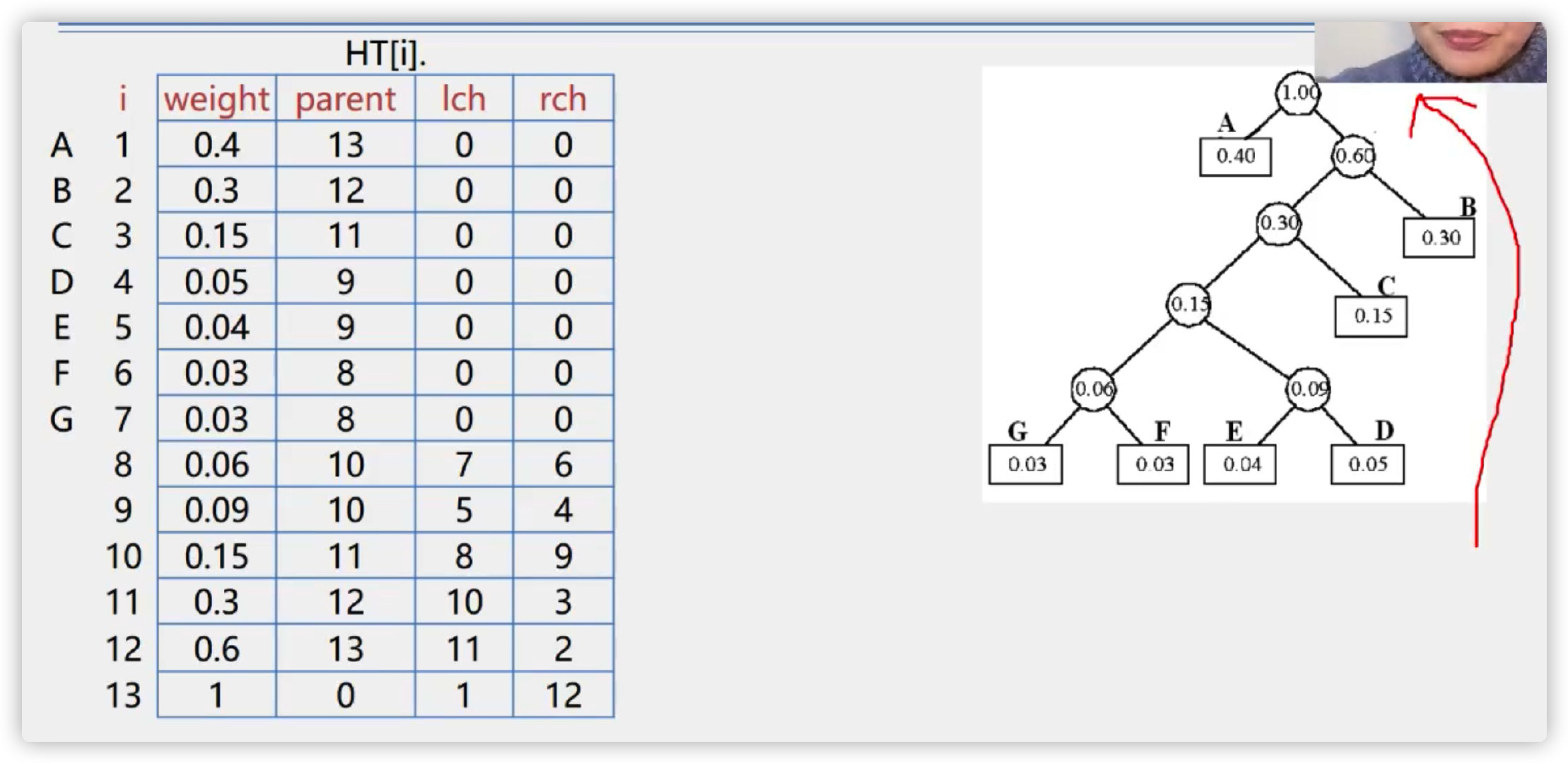
Implementation of Huffman coding algorithm

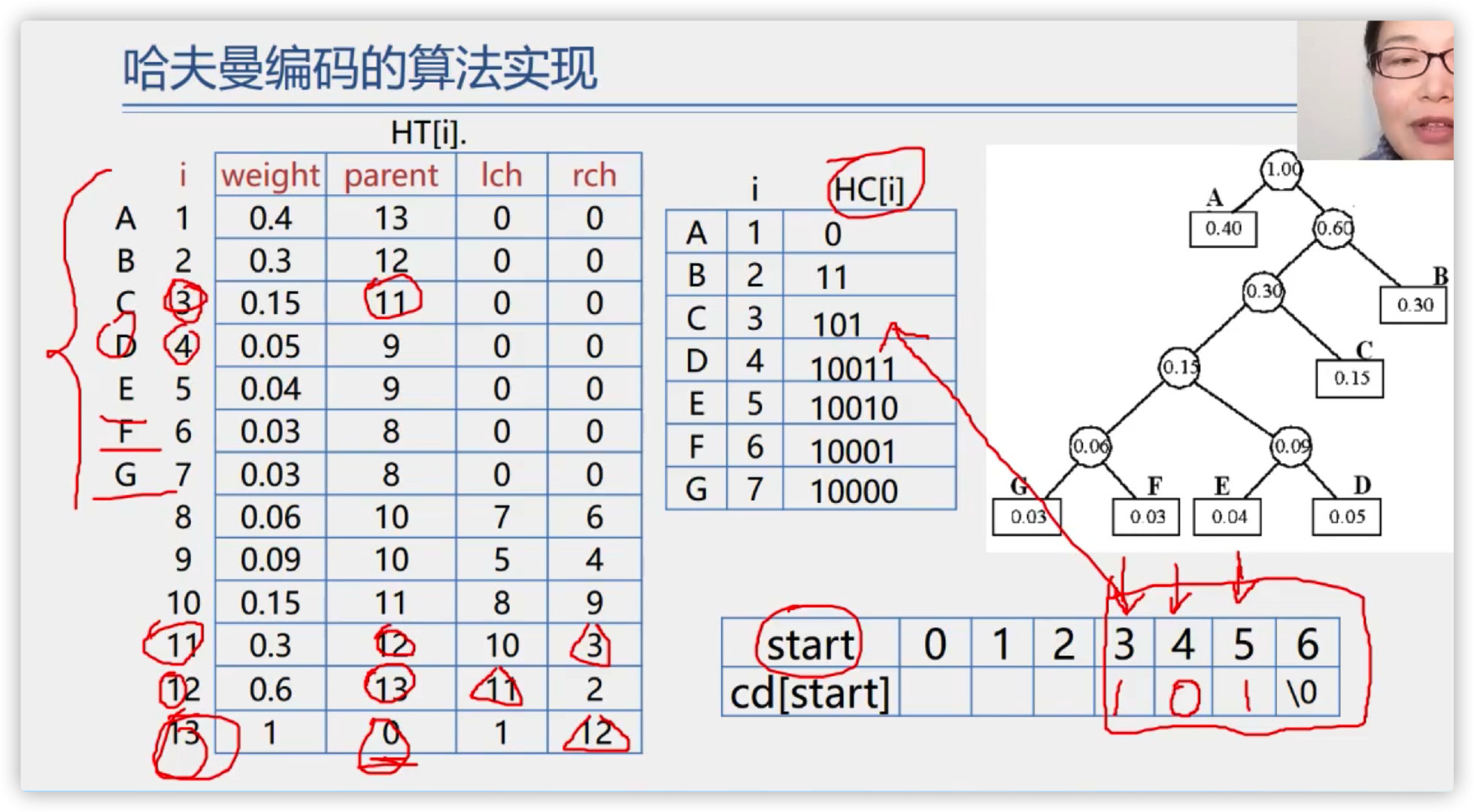
(6) Encoding and decoding of files

code

decode

example

2. Figure

(1) Concept

chart

Undirected graph

Directed graph

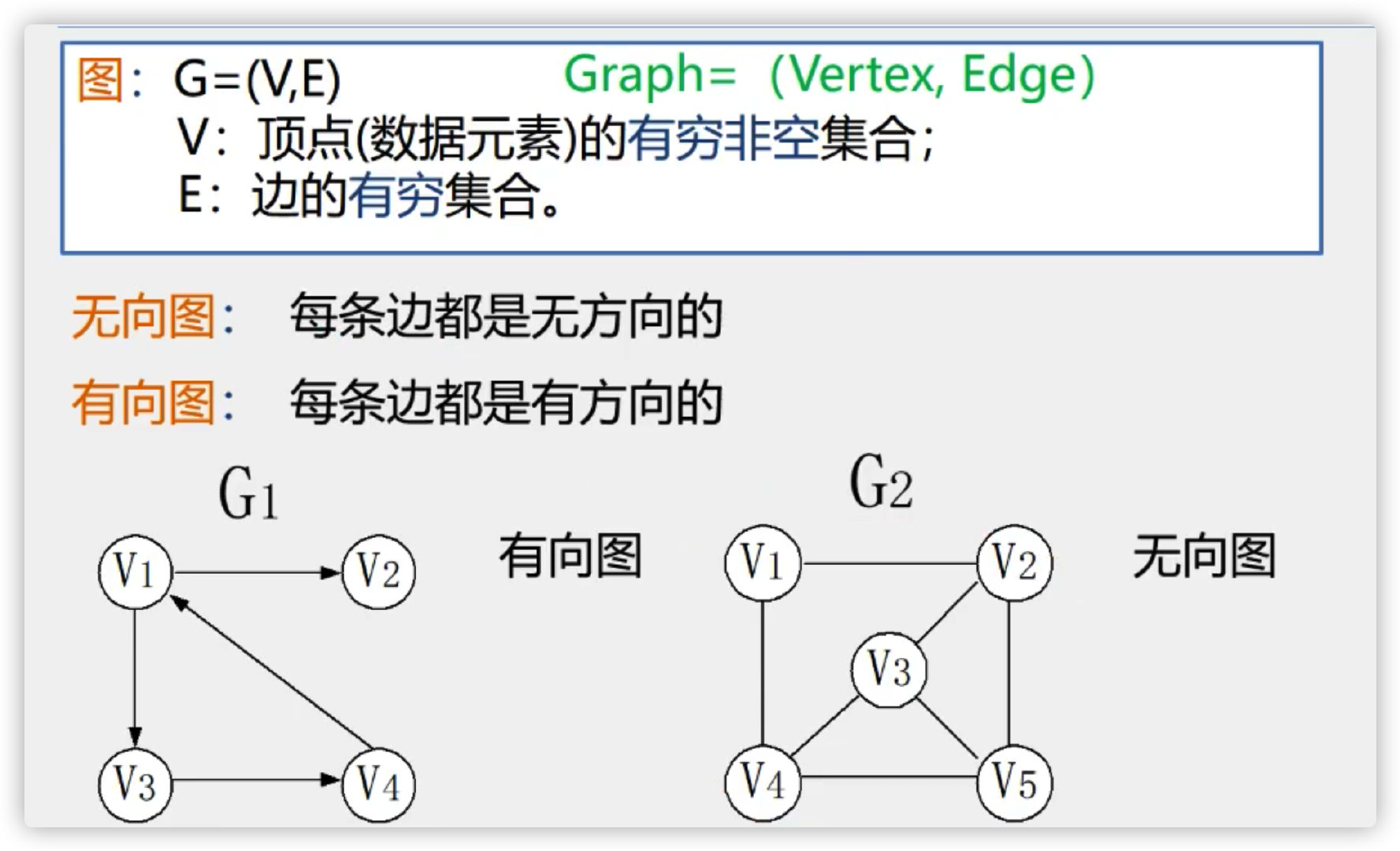
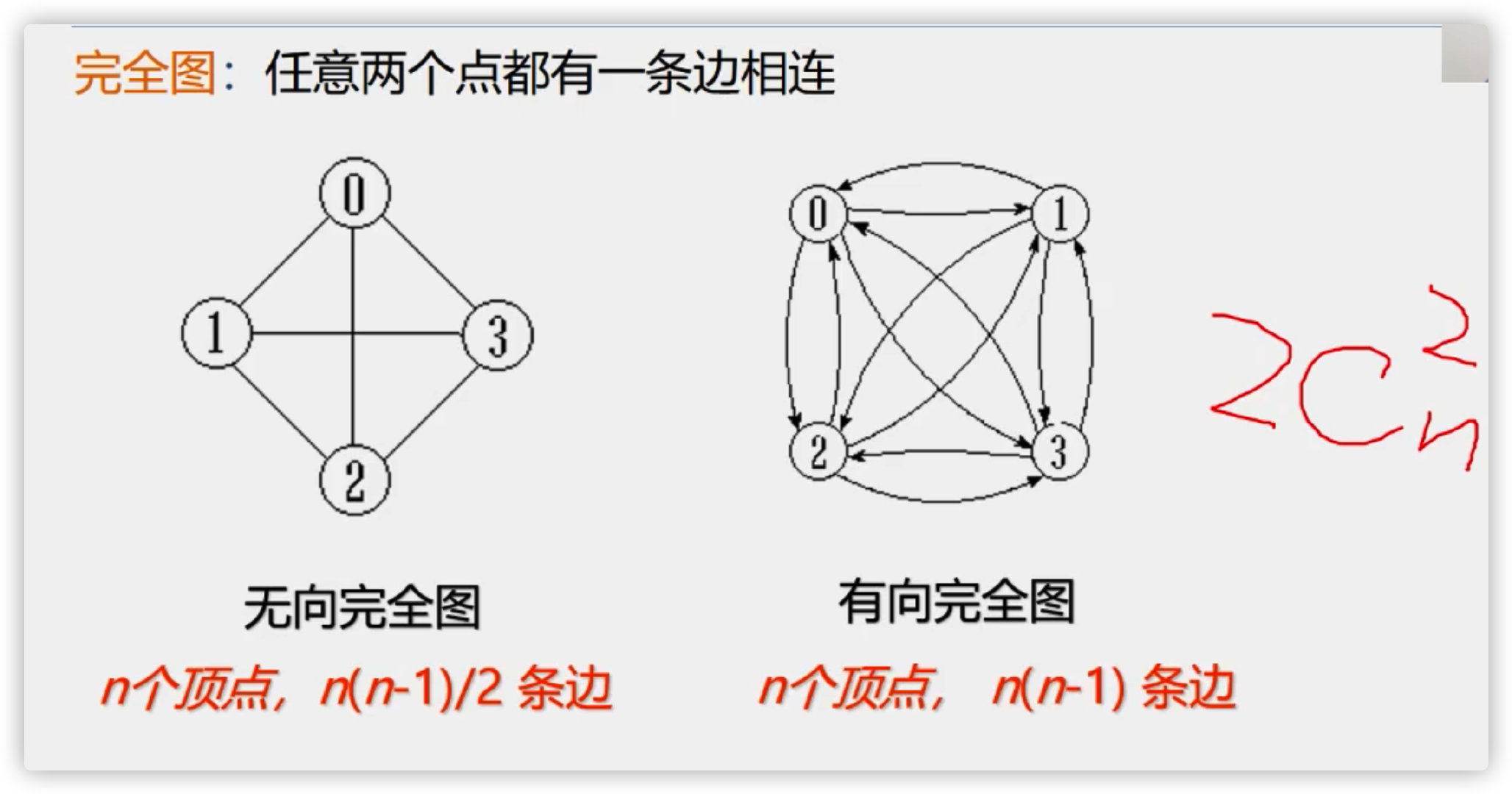
Complete graph

Sparse graph

Dense graph

network

Adjacency

Association (attachment)

Degree of fixed point

route

path length

route

path length

loop

Simple path

Simple return path (simple loop)

Connected graph (strongly connected graph)

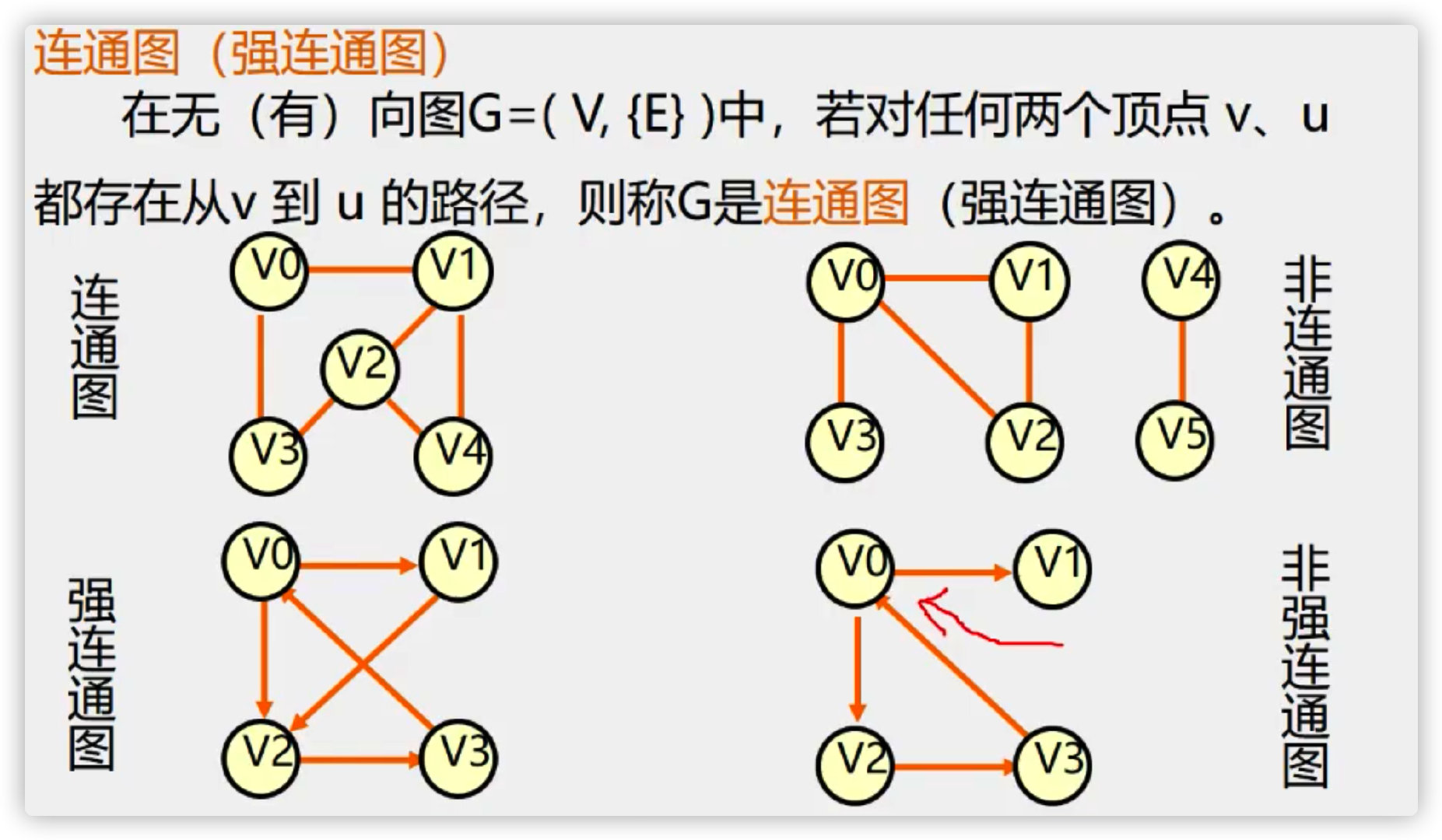
Power and network

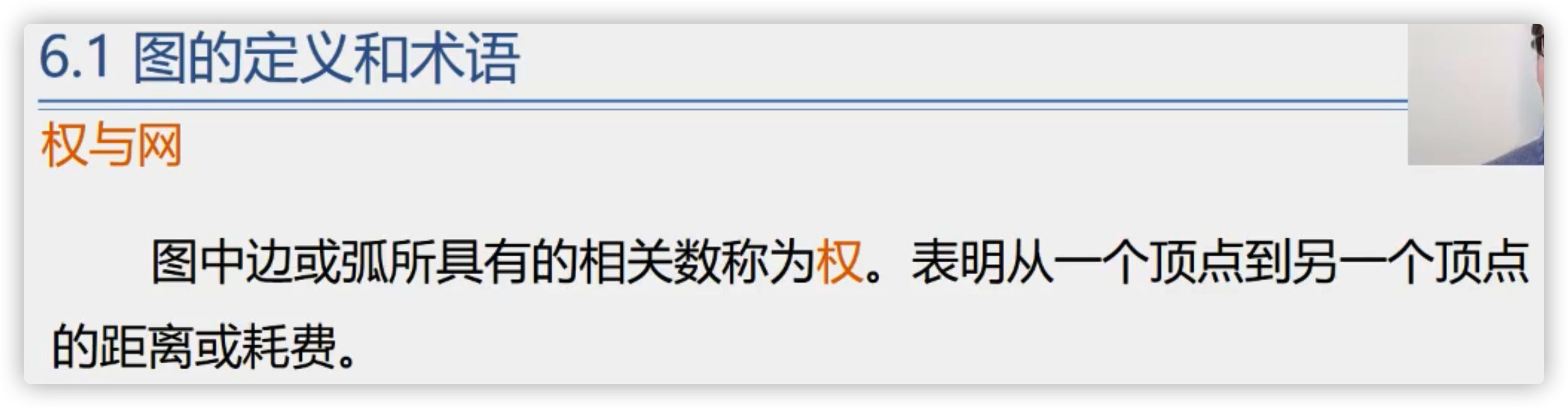
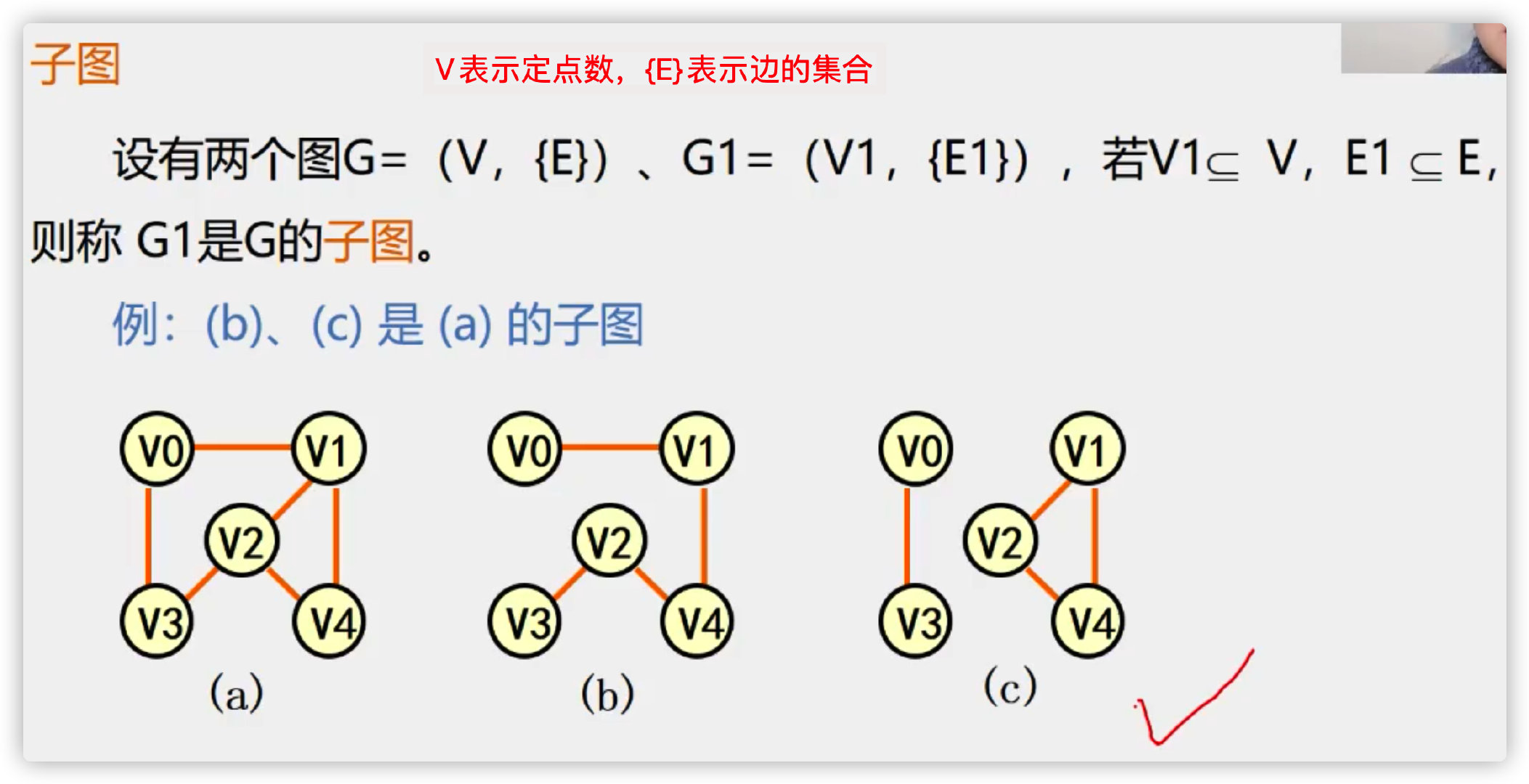
Subgraph

Connected component

Strongly connected component

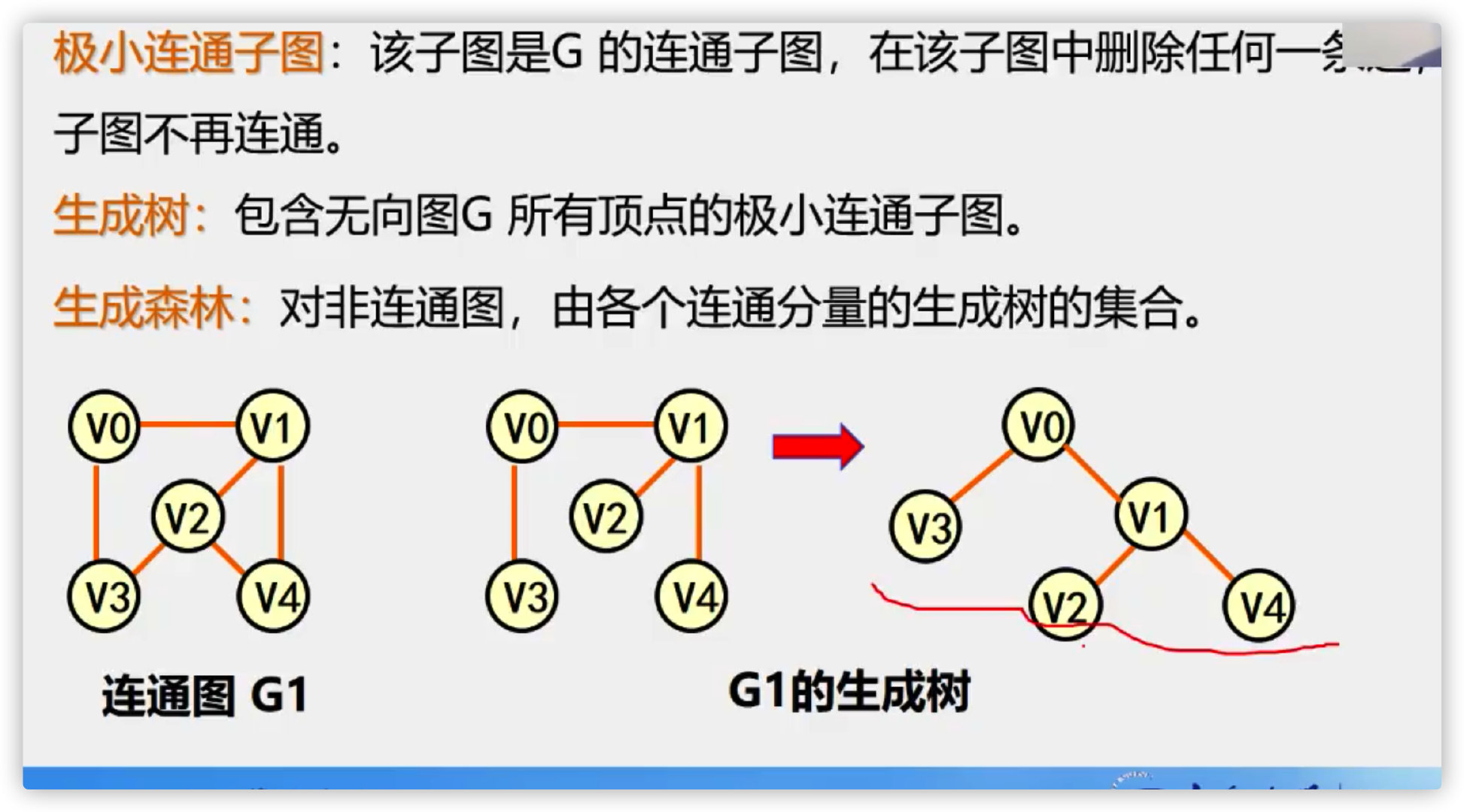
Minimal connected subgraph

Spanning tree

Generative forest

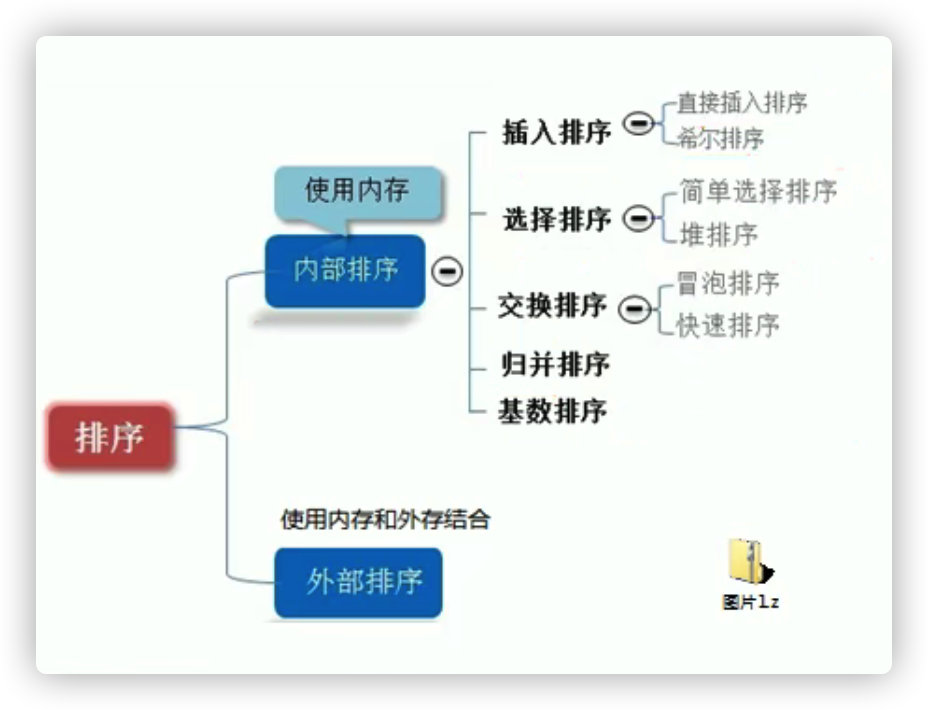
5, Sorting and finding

(1) . classification

Quick sort

#include <stdio.h>
/*
Quick sort
*/


//Function declaration
void sort(int *a, int low, int high);
int FindPos(int *a, int low, int high);
int main()
{
    int a[6] = {2, 1, 0, 5, 4, 3};
    sort(a, 0, 5); // 0 represents the subscript of the first element and 5 represents the subscript of the last element
    // Output results
    for (int i = 0; i < 6; i++)
    {
        printf("%d ", a[i]);
    }
}
void sort(int *a, int low, int high)
{
    int pos;

    if (low<high)
    {
        FindPos(a,low,high);
        sort(a,low,pos-1);
        sort(a,pos+1,high);
    }
    
}

int FindPos(int *a, int low, int high){
    int val = a[low];
    while(low<high){
        while(low<high && a[high]>=val){
            high--;
        }
        // assignment
        a[low] = a[high];

        while(low<high && a[low]<=val){
            low++;
        }
        // assignment
        a[high] = a[low];
    }
    a[low] = val;

    return low; // Low and high are OK. After termination, low and high must be equal
}