Destruction plan
Title Link: ybtoj high efficiency advanced 21169
General idea of the topic
Give you a tree, and then you need to find two paths without intersecting edges, so that after deleting the points of the two paths and their adjacent edges, the tree is divided into as many connected blocks as possible.
thinking
This is the classification of the underworld.
(more than ten pages of the caption are true * *)
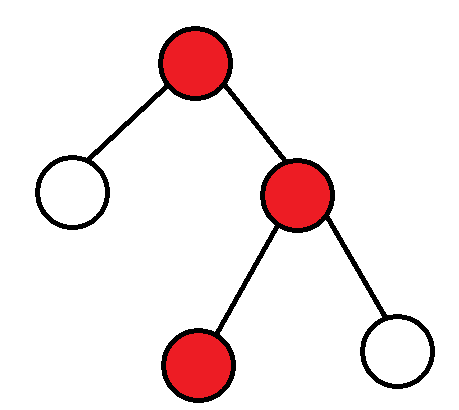
The first is to set f i , j f_{i,j} fi,j # yes i i In the subtree of i, the current form is j j The maximum number of connected blocks of j.
Then introduce the form:
0
0
0: an endpoint is at the current root
i
i
i. The other is in the subtree.
1
1
1: Not through
i
i
i. In
i
i
i is a chain in the subtree.

2
2
2: In
i
i
i a chain in the subtree, passing through
i
i
i point.

3
3
3: This is to select two chains, one is type
0
0
One of the 0 is a type
1
1
1.

Then we consider two questions:
How to count the answers? How to transfer
f
f
f array.
Continue the classification discussion and first consider solving the statistical answer.
There are six statistical answers.
(back) − [ u = = 1 ] -[u==1] − [u==1] because if there is something on the top of the root, there is a connected block; if there is nothing on the top, there is no connected block, so there is one missing)
First:
f
u
,
0
+
f
v
,
3
−
[
u
=
=
1
]
f_{u,0}+f_{v,3}-[u==1]
fu,0+fv,3−[u==1]

Second:
f
u
,
0
+
f
v
,
3
−
[
u
=
=
1
]
f_{u,0}+f_{v,3}-[u==1]
fu,0+fv,3−[u==1]

Third:
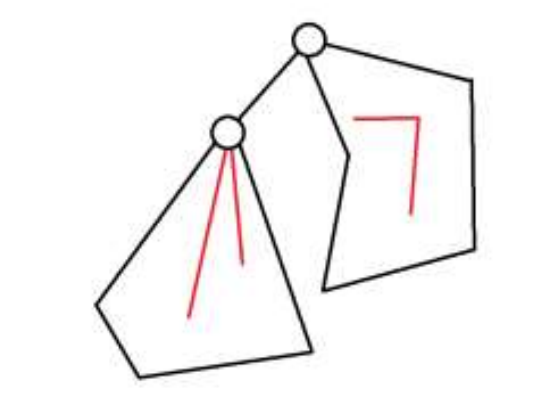
f
u
,
1
+
f
v
,
2
f_{u,1}+f_{v,2}
fu,1+fv,2
Fourth:
f
u
,
1
+
f
v
,
1
−
1
f_{u,1}+f_{v,1}-1
fu,1 + fv,1 − 1 (this minus one is one less than the above)

Fifth:
f
u
,
2
+
f
v
,
1
−
[
u
=
=
1
]
f_{u,2}+f_{v,1}-[u==1]
fu,2+fv,1−[u==1]
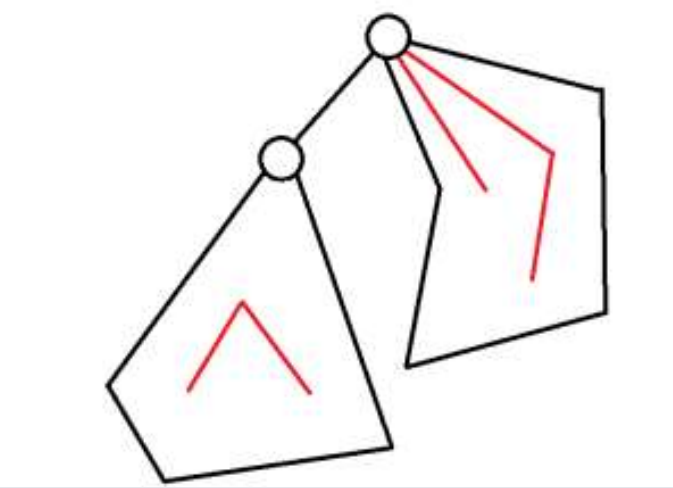
Sixth:
f
u
,
2
+
f
v
,
2
−
[
u
=
=
1
]
f_{u,2}+f_{v,2}-[u==1]
fu,2+fv,2−[u==1]

Then consider the transfer. (set here) d e g i deg_i degi is i i i (number of sons)
0
0
0:
There is only one way to extend more on the son's path
i
i
i this son.
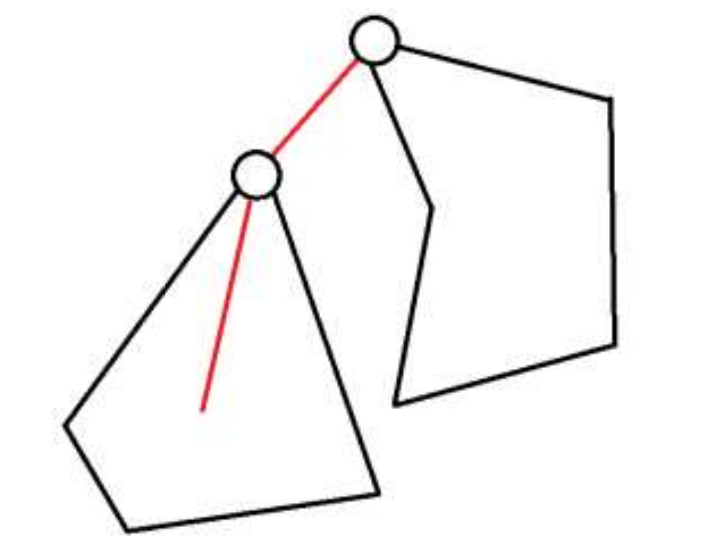
f
v
,
0
+
d
e
g
p
−
1
f_{v,0}+deg_p-1
fv,0+degp−1
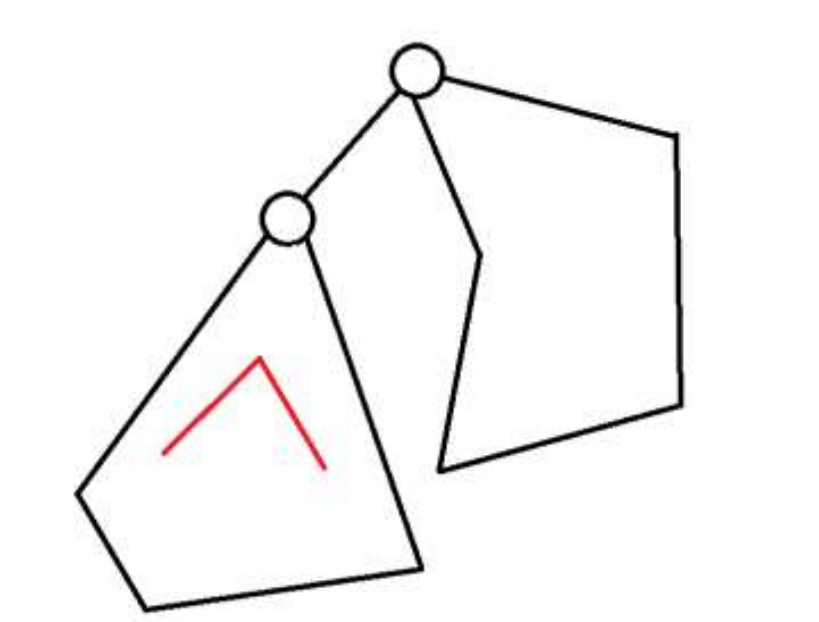
1
1
1:
Method 1:
f
v
,
1
f_{v,1}
fv,1
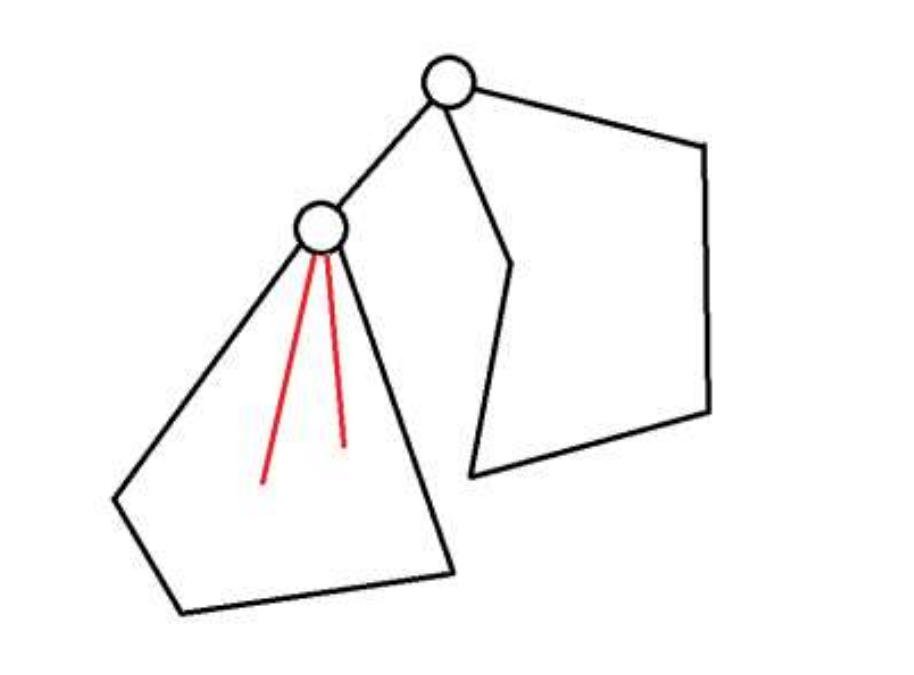
Method 2:
f
v
,
2
+
1
f_{v,2}+1
fv,2+1
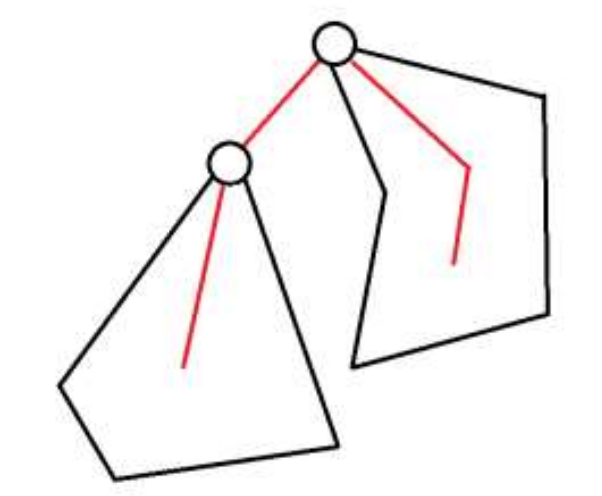
2
2
2:
One way,
f
u
,
0
+
f
v
,
0
−
1
f_{u,0}+f_{v,0}-1
fu,0+fv,0−1
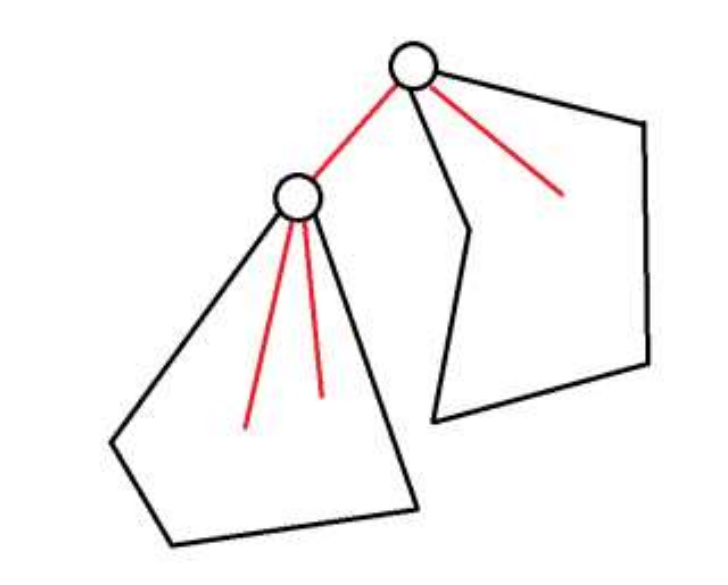
3
3
3:
Method 1:
f
u
,
0
+
f
v
,
2
−
1
f_{u,0}+f_{v,2}-1
fu,0+fv,2−1
Method 2:
f
u
,
0
+
f
v
,
1
−
1
f_{u,0}+f_{v,1}-1
fu,0+fv,1−1
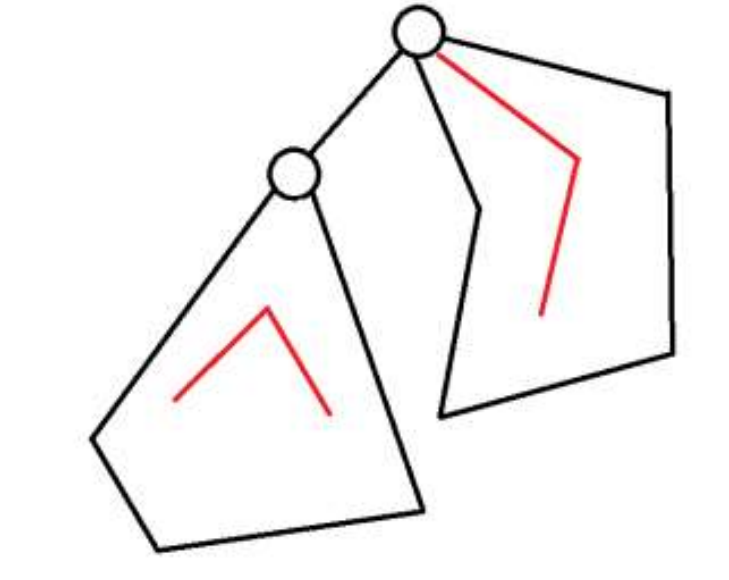
Method 3:
f
u
,
2
+
f
v
,
0
−
1
f_{u,2}+f_{v,0}-1
fu,2+fv,0−1
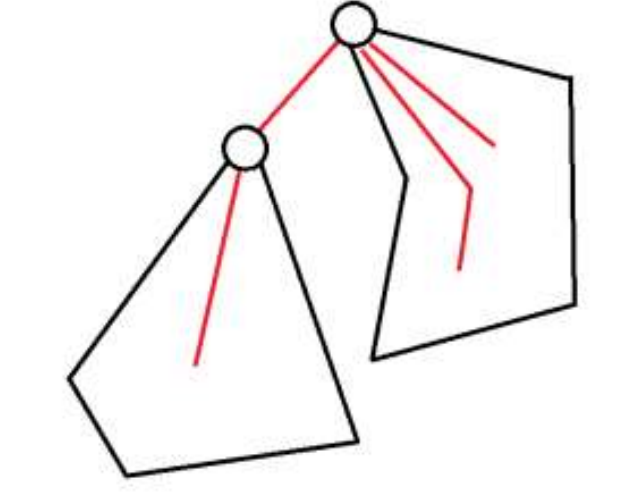
Method 4:
f
v
,
3
+
d
e
g
u
−
1
f_{v,3}+deg_u-1
fv,3+degu−1
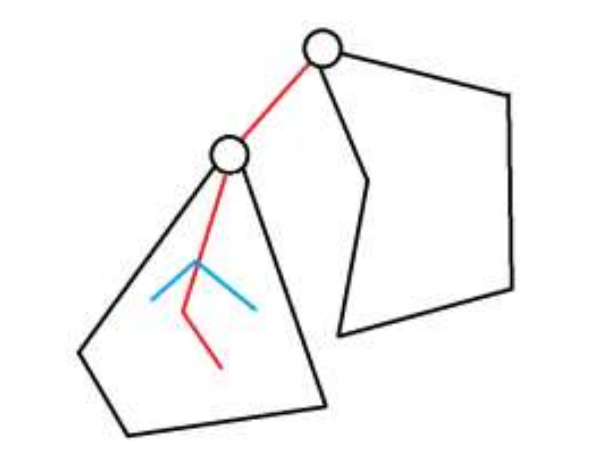
Method 5:
f
v
,
0
+
d
e
g
u
+
m
a
x
n
−
2
f_{v,0}+deg_u+maxn-2
fv,0+degu+maxn−2(
m
a
x
n
maxn
maxn is traversed before
v
v
Maximum in v
f
v
,
1
,
f
v
,
2
f_{v,1},f_{v,2}
fv,1,fv,2)
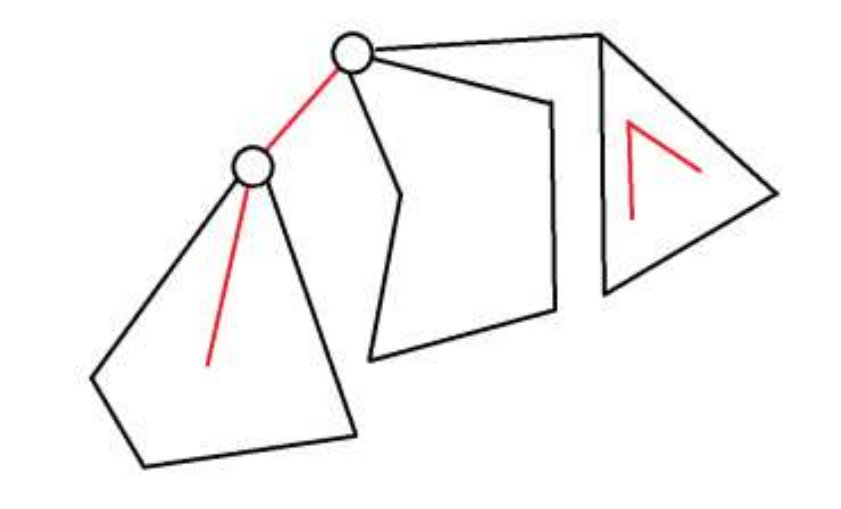
Then pay attention to the order of enumeration, and put the statistical answer first, and then
3
3
3 to be in
0
,
2
0,2
Before 0,2,
2
2
2 to be in
0
0
Between 0.
(because it is used, the modified one cannot be used, but the one before the modification)
code
#include<cstdio>
#include<iostream>
using namespace std;
struct node {
int to, nxt;
}e[1000005];
int T, X, n, x, y;
int le[500005], KK;
int deg[500005], ans;
int f[500005][5];
void csh() {
KK = 0; ans = 0;
for (int i = 1; i <= n; i++) le[i] = 0, deg[i] = 0;
}
void add(int x, int y) {
e[++KK] = (node){y, le[x]}; le[x] = KK;
e[++KK] = (node){x, le[y]}; le[y] = KK;
}
void DP(int now, int father) {
f[now][0] = f[now][2] = f[now][3] = deg[now];
f[now][1] = 1;
int maxn = 0;
for (int i = le[now]; i; i = e[i].nxt)
if (e[i].to != father) {
DP(e[i].to, now);
ans = max(ans, f[now][3] + f[e[i].to][0] - (now == 1));
ans = max(ans, f[now][0] + f[e[i].to][3] - (now == 1));
ans = max(ans, f[now][1] + f[e[i].to][2]);
ans = max(ans, f[now][1] + f[e[i].to][1] - 1);
ans = max(ans, f[now][2] + f[e[i].to][1] - (now == 1));
ans = max(ans, f[now][2] + f[e[i].to][2] - (now == 1));
f[now][1] = max(f[now][1], f[e[i].to][1]);
f[now][1] = max(f[now][1], f[e[i].to][2] + 1);
f[now][3] = max(f[now][3], f[now][0] + f[e[i].to][2] - 1);
f[now][3] = max(f[now][3], f[now][0] + f[e[i].to][1] - 1);
f[now][3] = max(f[now][3], f[now][2] + f[e[i].to][0] - 1);
f[now][3] = max(f[now][3], f[e[i].to][3] + deg[now] - 1);
f[now][3] = max(f[now][3], f[e[i].to][0] + deg[now] + maxn - 2);
f[now][2] = max(f[now][2], f[now][0] + f[e[i].to][0] - 1);
f[now][0] = max(f[now][0], f[e[i].to][0] + deg[now] - 1);
maxn = max(maxn, max(f[e[i].to][1], f[e[i].to][2]));
}
}
int main() {
// freopen("destroy.in", "r", stdin);
// freopen("destroy.out", "w",stdout);
scanf("%d %d", &T, &X);
while (T--) {
scanf("%d", &n);
if (X >= 1) scanf("%d %d", &x, &y);
if (X >= 2) scanf("%d %d", &x, &y);
for (int i = 1; i < n; i++) {
scanf("%d %d", &x, &y);
add(x, y);
deg[x]++; deg[y]++;
}
for (int i = 2; i <= n; i++) deg[i]--;
DP(1, 0);
printf("%d\n", ans);
csh();
}
return 0;
}