# -*- coding: utf-8 -*- from collections import Counter from linear_algebra import sum_of_squares, dot import math import matplotlib.pyplot as plt from pylab import mpl mpl.rcParams['font.sans-serif'] = ['SimHei'] num_friends = [100,49,41,40,25,21,21,19,19,18,18,16,15,15,15,15,14,14,13,13,13,13,12,12,11,10,10,10,10,10,10,10,10,10,10,10,10,10,10,10,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,9,8,8,8,8,8,8,8,8,8,8,8,8,8,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1] def make_friend_counts_histogram(plt): friend_counts = Counter(num_friends) xs = range(101) ys = [friend_counts[x] for x in xs] plt.bar(xs, ys) plt.axis([0,101,0,25]) plt.title("Histogram of friends") plt.xlabel("Number of friends") plt.ylabel("Number") plt.show() num_points = len(num_friends) # 204 largest_value = max(num_friends) # 100 smallest_value = min(num_friends) # 1 sorted_values = sorted(num_friends) smallest_value = sorted_values[0] # 1 second_smallest_value = sorted_values[1] # 1 second_largest_value = sorted_values[-2] # 49 # this isn't right if you don't from __future__ import division def mean(x): return sum(x) / len(x) # Do not sort the method of calculating the median: https://en.wikipedia.org/wiki/Quickselect def median(v): """Median finding""" n = len(v) sorted_v = sorted(v) midpoint = n // 2 if n % 2 == 1: # If it is an odd number, return the middle value return sorted_v[midpoint] else: # If it is an even number, return the mean value of the middle two values lo = midpoint - 1 hi = midpoint return (sorted_v[lo] + sorted_v[hi]) / 2 def quantile(x, p): """returns the pth-percentile value in x""" p_index = int(p * len(x)) return sorted(x)[p_index] def mode(x): """returns a list, might be more than one mode""" counts = Counter(x) max_count = max(counts.values()) return [x_i for x_i, count in counts.items() if count == max_count] # Discreteness is a measure of the degree of data discreteness. In general, if it counts values close to zero, it indicates data aggregation # Together, the degree of dispersion is small, and if the value is large (whatever that means), it means that the data is very discrete. def data_range(x): return max(x) - min(x) def de_mean(x): """translate x by subtracting its mean (so the result has mean 0)""" x_bar = mean(x) return [x_i - x_bar for x_i in x] def variance(x): """assumes x has at least two elements""" n = len(x) deviations = de_mean(x) return sum_of_squares(deviations) / (n - 1) def standard_deviation(x): return math.sqrt(variance(x)) def interquartile_range(x): return quantile(x, 0.75) - quantile(x, 0.25) #### # # CORRELATION # ##### daily_minutes = [1,68.77,51.25,52.08,38.36,44.54,57.13,51.4,41.42,31.22,34.76,54.01,38.79,47.59,49.1,27.66,41.03,36.73,48.65,28.12,46.62,35.57,32.98,35,26.07,23.77,39.73,40.57,31.65,31.21,36.32,20.45,21.93,26.02,27.34,23.49,46.94,30.5,33.8,24.23,21.4,27.94,32.24,40.57,25.07,19.42,22.39,18.42,46.96,23.72,26.41,26.97,36.76,40.32,35.02,29.47,30.2,31,38.11,38.18,36.31,21.03,30.86,36.07,28.66,29.08,37.28,15.28,24.17,22.31,30.17,25.53,19.85,35.37,44.6,17.23,13.47,26.33,35.02,32.09,24.81,19.33,28.77,24.26,31.98,25.73,24.86,16.28,34.51,15.23,39.72,40.8,26.06,35.76,34.76,16.13,44.04,18.03,19.65,32.62,35.59,39.43,14.18,35.24,40.13,41.82,35.45,36.07,43.67,24.61,20.9,21.9,18.79,27.61,27.21,26.61,29.77,20.59,27.53,13.82,33.2,25,33.1,36.65,18.63,14.87,22.2,36.81,25.53,24.62,26.25,18.21,28.08,19.42,29.79,32.8,35.99,28.32,27.79,35.88,29.06,36.28,14.1,36.63,37.49,26.9,18.58,38.48,24.48,18.95,33.55,14.24,29.04,32.51,25.63,22.22,19,32.73,15.16,13.9,27.2,32.01,29.27,33,13.74,20.42,27.32,18.23,35.35,28.48,9.08,24.62,20.12,35.26,19.92,31.02,16.49,12.16,30.7,31.22,34.65,13.13,27.51,33.2,31.57,14.1,33.42,17.44,10.12,24.42,9.82,23.39,30.93,15.03,21.67,31.09,33.29,22.61,26.89,23.48,8.38,27.81,32.35,23.84] def covariance(x, y): n = len(x) return dot(de_mean(x), de_mean(y)) / (n - 1) def correlation(x, y): stdev_x = standard_deviation(x) stdev_y = standard_deviation(y) if stdev_x > 0 and stdev_y > 0: return covariance(x, y) / stdev_x / stdev_y else: return 0 # if no variation, correlation is zero outlier = num_friends.index(100) # index of outlier num_friends_good = [x for i, x in enumerate(num_friends) if i != outlier] daily_minutes_good = [x for i, x in enumerate(daily_minutes) if i != outlier] if __name__ == "__main__": make_friend_counts_histogram(plt) print("num_points", len(num_friends)) print("largest value", max(num_friends)) print("smallest value", min(num_friends)) print("second_smallest_value", sorted_values[1]) print("second_largest_value", sorted_values[-2] ) print("mean(num_friends)", mean(num_friends)) print("median(num_friends)", median(num_friends)) print("quantile(num_friends, 0.10)", quantile(num_friends, 0.10)) print("quantile(num_friends, 0.25)", quantile(num_friends, 0.25)) print("quantile(num_friends, 0.75)", quantile(num_friends, 0.75)) print("quantile(num_friends, 0.90)", quantile(num_friends, 0.90)) print("mode(num_friends)", mode(num_friends)) print("data_range(num_friends)", data_range(num_friends)) print("variance(num_friends)", variance(num_friends)) print("standard_deviation(num_friends)", standard_deviation(num_friends)) print("interquartile_range(num_friends)", interquartile_range(num_friends)) print("covariance(num_friends, daily_minutes)", covariance(num_friends, daily_minutes)) print("correlation(num_friends, daily_minutes)", correlation(num_friends, daily_minutes)) print("correlation(num_friends_good, daily_minutes_good)", correlation(num_friends_good, daily_minutes_good))
results of enforcement
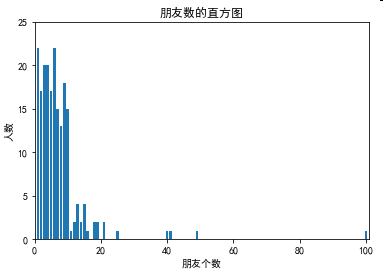
num_points 204 largest value 100 smallest value 1 second_smallest_value 1 second_largest_value 49 mean(num_friends) 7.333333333333333 median(num_friends) 6.0 quantile(num_friends, 0.10) 1 quantile(num_friends, 0.25) 3 quantile(num_friends, 0.75) 9 quantile(num_friends, 0.90) 13 mode(num_friends) [6, 1] data_range(num_friends) 99 variance(num_friends) 81.54351395730716 standard_deviation(num_friends) 9.03014473623248 interquartile_range(num_friends) 6 covariance(num_friends, daily_minutes) 22.425435139573064 correlation(num_friends, daily_minutes) 0.24736957366478218 correlation(num_friends_good, daily_minutes_good) 0.5736792115665573
In fact, NumPy has implemented the above functions. More python data analysis Libraries
Lovely python test development library Please like github, thank you!
Summary of python Chinese Library Documents
[Xuefeng magnetic needle stone blog] python3 standard library - Chinese version
[Xuefeng magnetite blog] python3 quick start tutorial
Interface automation performance test online training program
Automatic test data analysis of python test development
Please pay attention to more Xuefeng magnetic needle stone: a brief book
Technical support qq group: 144081101 (the group files will be recorded in the video later) 591302926567351477 nail free group: 21745728
Taoist technology - palmistry, hand examination, Chinese medicine and other nail groups 21734177 qq group: 391441566 184175668 338228106, hand examination, face examination, tongue examination, lottery, constitution identification. The service fee is 50 yuan per person. Please contact pin or wechat Python