Agisoft Photoscan / Mateshape is a high-quality three-dimensional modeling software using photos. It only needs a few photos to reconstruct the scene sparsely and densely. Photoscan reconstruction results can be derived in the form of point cloud (.ply) and camera parameters (.xml). The basic structure of camera parameters file is as follows:

<?xml version="1.0" encoding="UTF-8"?>
<document version="1.5.0">
  <chunk label="Chunk 2" enabled="1">
    <sensors next_id="2">
      <sensor id="0" label="unknown" type="frame">
        <resolution width="2256" height="1504"/>
        <property name="fixed" value="0"/>
        <property name="layer_index" value="0"/>
        <bands>
          <band label="Red"/>
          <band label="Green"/>
          <band label="Blue"/>
        </bands>
        <data_type>uint8</data_type>
        <calibration type="frame" class="adjusted">
          <resolution width="2256" height="1504"/>
          <f>1940.44326476953</f>
          <cx>13.1749075726049</cx>
          <cy>9.90781070951072</cy>
          <k1>-0.105652576294122</k1>
          <k2>0.181325297027899</k2>
          <k3>-0.0592964727618129</k3>
          <p1>0.00206081605079198</p1>
          <p2>0.000470042919918441</p2>
        </calibration>
        <covariance>
          <params>f cx cy k1 k2 k3 p1 p2</params>
          <coeffs>2.0733588750258165e+000 3.3929432732417547e-001 -3.1733835341771577e-001 -5.4658442369333565e-004 3.0370081230896582e-003 -3.1356947110278534e-003 5.2705435197758904e-005 -5.1942928435856751e-005 3.3929432732417547e-001 2.9030120242126229e+000 -4.4783334115597678e-001 -5.4006412558368184e-004 2.7492718459672764e-003 -3.8449923065214616e-003 4.2175020229014983e-004 -2.4276678093922544e-005 -3.1733835341771577e-001 -4.4783334115597678e-001 3.6157751348946210e+000 -7.6302558122755184e-004 2.6559814107009433e-003 -3.2660344589292524e-003 -6.2426016405221110e-005 1.9002231854318343e-004 -5.4658442369333565e-004 -5.4006412558368184e-004 -7.6302558122755184e-004 6.7239409985664287e-006 -2.9151947830055737e-005 3.8848928879691912e-005 -7.3700638646021470e-008 -6.9366476152724520e-008 3.0370081230896582e-003 2.7492718459672764e-003 2.6559814107009433e-003 -2.9151947830055737e-005 1.3648458206350376e-004 -1.8944698692176858e-004 3.5354142426803448e-007 1.5383589402715499e-007 -3.1356947110278534e-003 -3.8449923065214616e-003 -3.2660344589292524e-003 3.8848928879691912e-005 -1.8944698692176858e-004 2.7211205766284002e-004 -4.7559541398024204e-007 -1.7375904955674177e-007 5.2705435197758904e-005 4.2175020229014983e-004 -6.2426016405221110e-005 -7.3700638646021470e-008 3.5354142426803448e-007 -4.7559541398024204e-007 9.3242309621928652e-008 -1.5342544835203691e-009 -5.1942928435856751e-005 -2.4276678093922544e-005 1.9002231854318343e-004 -6.9366476152724520e-008 1.5383589402715499e-007 -1.7375904955674177e-007 -1.5342544835203691e-009 3.4030427227067055e-008</coeffs>
        </covariance>
 <cameras next_id="26" next_group_id="0">
      <camera id="0" sensor_id="0" label="00000000" enabled="1">
        <transform>9.7295244355931876e-001 -2.4137605644869383e-002 -2.2974098146757183e-001 2.3001938083983617e+000 -1.5022238929850992e-002 -9.9903205136995099e-001 4.1343592890339495e-002 -2.9793714733084692e-001 -2.3051653934042321e-001 -3.6774125812593164e-002 -9.7237327645366456e-001 -4.5274423068157277e-001 0.0000000000000000e+000 0.0000000000000000e+000 0.0000000000000000e+000 1.0000000000000000e+000</transform>

Here we make a simple agreement on the internal and external parameters of the camera. When using a simple pinhole camera model, the projection formula from three-dimensional point Pc = Xc, Yc, Zc to image point p= (mu, _) is as follows: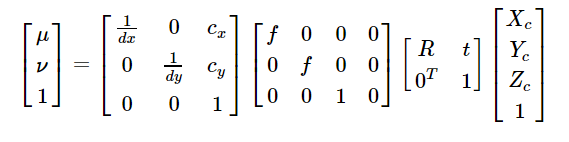

The internal parameters of the camera include: dx, dy is the width and height of the pixels, f is the focal length of the camera, cx, cy is the position of the center of light;
External parameters of the camera include: 3 x 3 rotation matrix R and 3 x 1 translation matrix T, which represent the transformation from world coordinate system to camera coordinate system.

When projecting directly according to the point cloud coordinates and the camera parameters given in the xml file, a large deviation will be found. After several weeks of groping, it is found that the correct way to use the camera parameters is as follows:

f = 1940.443

cx = 2256 / 2 + 13.175

cy = 1504 / 2 + 9.908

Rt = [9.729e-001, -2.414e-002, -2.297e-001, 2.300e+000,
-1.502e-002, -9.990e-001, 4.134e-002, -2.979e-001,
-2.305e-001, -3.677e-002, -9.724e-001 -4.527e-001,
0, 0, 0, 1] -1

That is to say, the actual optical center position is 0.5*width/0.5*height+cx/cy of the image.
The rotation translation matrix of the actual camera is inversed after the 16 elements in transform are composed of 4 *4 matrix.

Refs:
[1] https://www.agisoft.com/forum/index.php?topic=2351.0
[2] https://www.cnblogs.com/wangguchangqing/p/8126333.html