In the last article, I left some questions. Although I have added a setting "bomb", the location around the bomb is not passable, but the number of bombs is still too small, so it's a bit monotonous. If I want to enrich the game, I need to increase the number of bombs. There is a problem here. If the location of the bomb is random, the bomb may block the way and cause a dead end. The problem of how many bombs can be on the m × n canvas mentioned in the previous article is not very meaningful, such as the following figure:

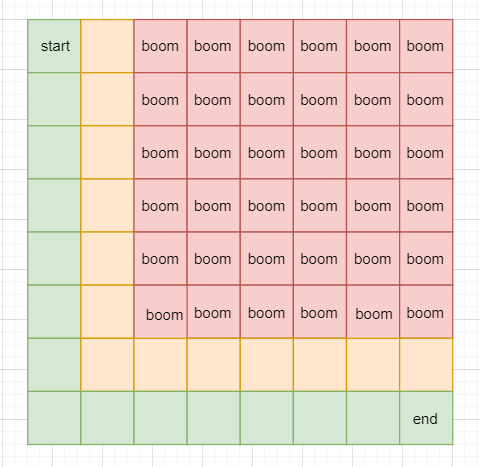
This arrangement is the case with the most bombs, but it's useless. Our question should be at least how many bombs can cause death. At least two bombs can cause a dead end, but we have dealt with this characteristic situation - there can be no bombs around the starting point and the ending point. In addition to this special situation, at least a few bombs can cause death. It is not hard to think of the following situations:

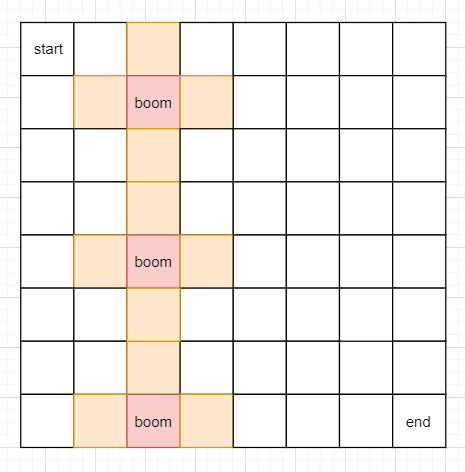
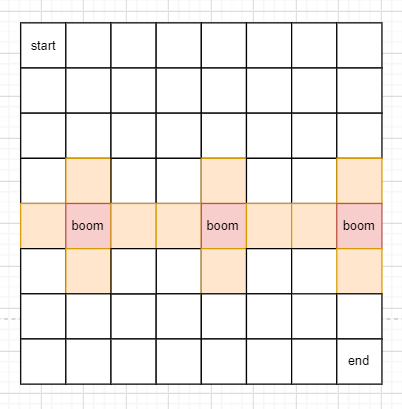
Let's describe the rule. Take the minimum min between m and n, min divided by 3. If it's divided by an integer, it's min/3. If there's a remainder, it's min/3+1. So as long as it is less than min, the bomb can be placed arbitrarily.

Change the code as follows:

func GetRoundParams(round int) RoundParams {
    once.Do(func() {
        roundParams = RoundParams{
            Height:  10,
            Width:   10,
            BoomNum: 1,
            BoomPosition: [][]int{
                {5, 5},
            },
        }
        switch round {
        case 1:
            roundParams = RoundParams{
                Height:     10,
                Width:      10,
                StartPoint: []int{0, 0},
                EndPoint:   []int{9, 9},
            }
            roundParams.BoomNum = minBooms(roundParams.Height, roundParams.Width)
            bp := make([][]int,0)
            tp := make([][]int,0)
                        rand.Seed(time.Now().UnixNano())
            for i := 0; i < roundParams.BoomNum - 1; i++ {
                x := rand.Intn(roundParams.Width-3) + 2
                y := rand.Intn(roundParams.Height-3) + 2
                bp = append(bp, []int{x, y})
                tp = append(tp, []int{x - 1, y}, []int{x + 1, y}, []int{x, y - 1}, []int{x, y + 1},)
            }
            roundParams.BoomPosition = bp
            roundParams.TrapPosition = tp
        }
    })

    return roundParams
}

func minBooms(h, w int) int {
    min := h
    if h-w > 0 {
        min = h
    }
    boomNum := min / 3
    if boomNum%3 != 0 {
        boomNum++
    }
    return boomNum
}

There is a certain probability that there will be repeated bomb positions, but this is not a problem and can be ignored. Take a look at the actual renderings:

Well Some of them are unsatisfactory. Although the location of the bombs can be arbitrary, the number seems to be too small. There is no difficulty. There is no difference between one and two. It's not rich enough to pass without thinking. Keep this problem for the next article.

Welcome to my official account: onepunchgo, leave a message for me.