(previously: WIN10 professional + QT5.15.2: control promotion - CSDN blog / / reference: function introduction of "promotion to..." in qt creator - Snail - blog Garden 1. Create a new project 2. Open the file: mainwindow.ui - > drag a tree widget control to the canvas - > right click the pop-up dialogue box - > Click "promotion to..." Option 3. Input https://www.cnblogs.com/woxinfeixiang2015/p/8260144.html )Well, control promotion is the derivation of a class. ××× Step 1: open IDE, QTCreator 5.0.0 (QT program is 5.15.2https://blog.csdn.net/wenluderen/article/details/120534315)

Control promotion in VS2019

×××

Step 1: open VS2019 and create a program. The path cannot have Chinese, and the name is: Test_IDE_VS_TiSheng

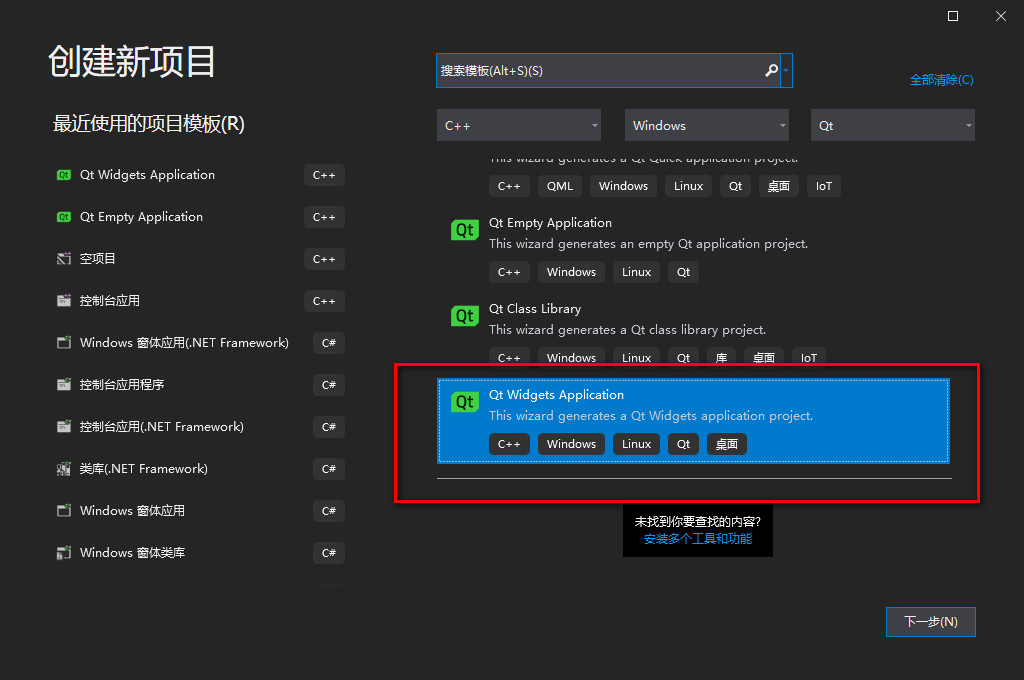
  Step 2: run it once to make sure there is no problem

Step 3: open the test_ide_vs_tisheng.ui file

Add Tree widget

****

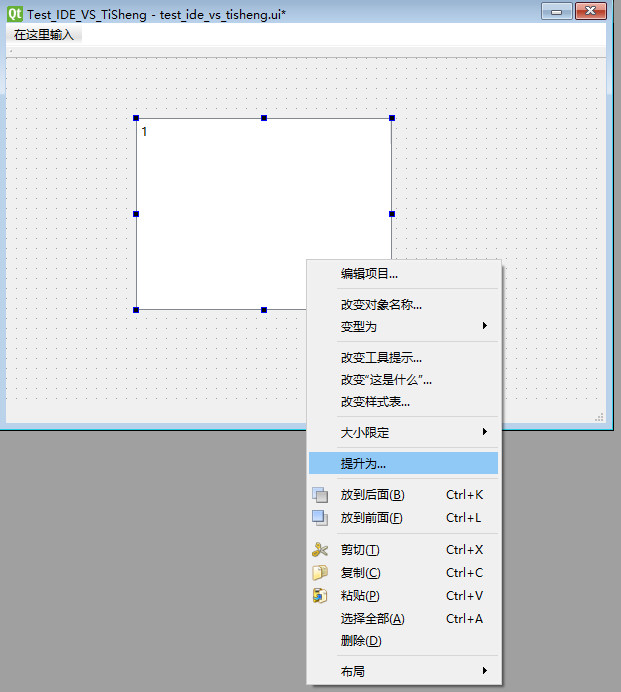
Open the file: test_ide_vs_tisheng.ui - > drag a tree widget control to the canvas - > right click the pop-up dialog box - > click the "promote to..." option

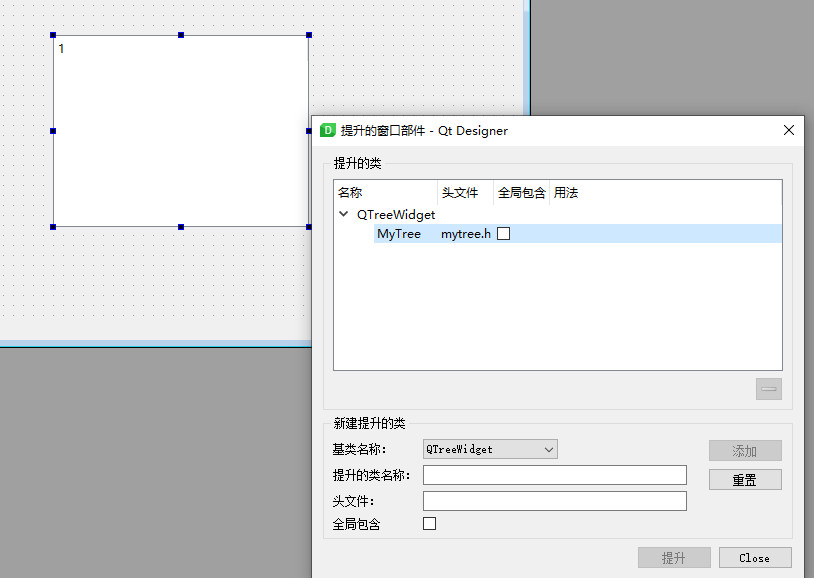
  Step 4: in the promoted type name position, enter   Mytree - > click the "add" button

  (so far, the operation in the UI has ended)

Header file: mytree.h   Source file: mytree.cpp

***

Step 5: compile and remind the following errors

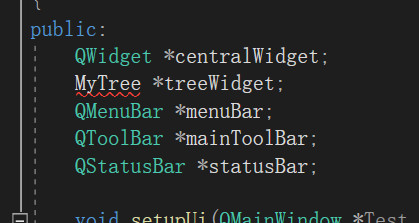
Just lack   The header file and source file corresponding to the MyTree class

×××××

Step 6: add classes manually

A:

 

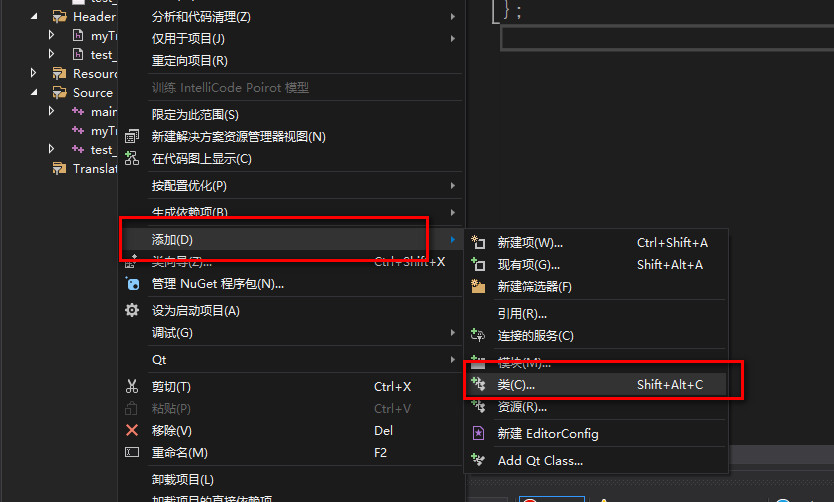
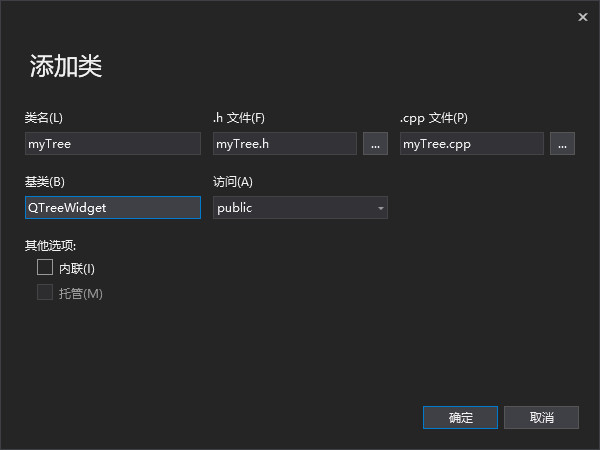
The effect is as follows

 

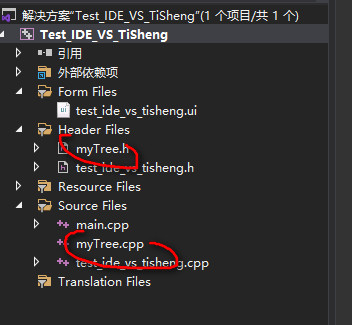
B: remember to supplement the header file, otherwise QTreeWidget cannot recognize it

××××

C: myTree.h

#pragma once
#include<QTreeWidget>
class myTree :
    public QTreeWidget
{
};

 ×××

D: myTree.cpp

#include "myTree.h"

××× In particular, the steps from a to D are wrong, but we don't delete them and put them in the blog because they are too easy to make. Here's how to correct them.

A: The preferred error reason is case

We open ui_test_ide_vs_tisheng.h

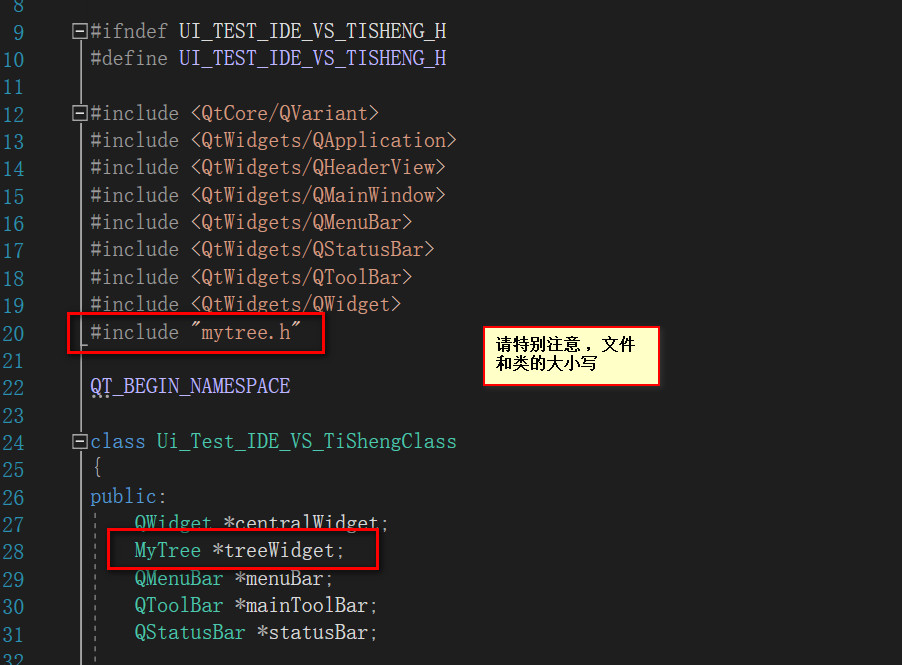
#include "mytree.h"

MyTree *treeWidget;

××

Therefore, we must also pay attention to this when adding classes later.

B: Completely eliminate the header file of the previously added class     And source files

 

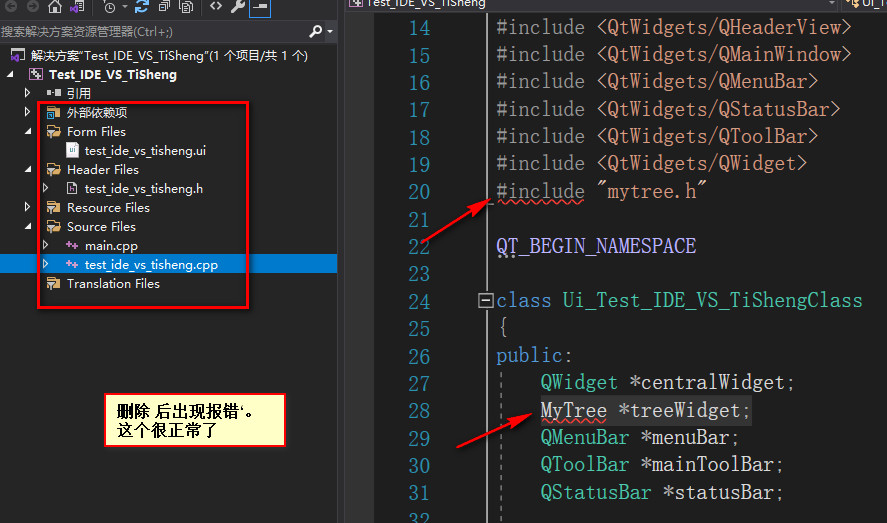
C: Add the class again

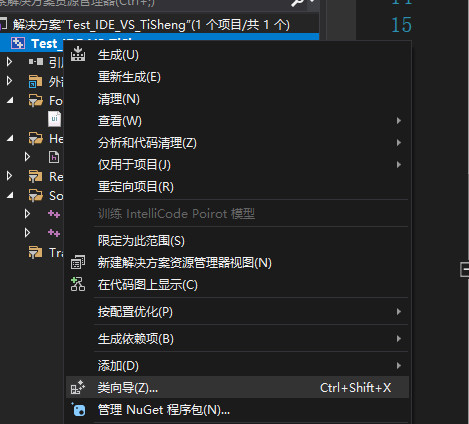
 D:

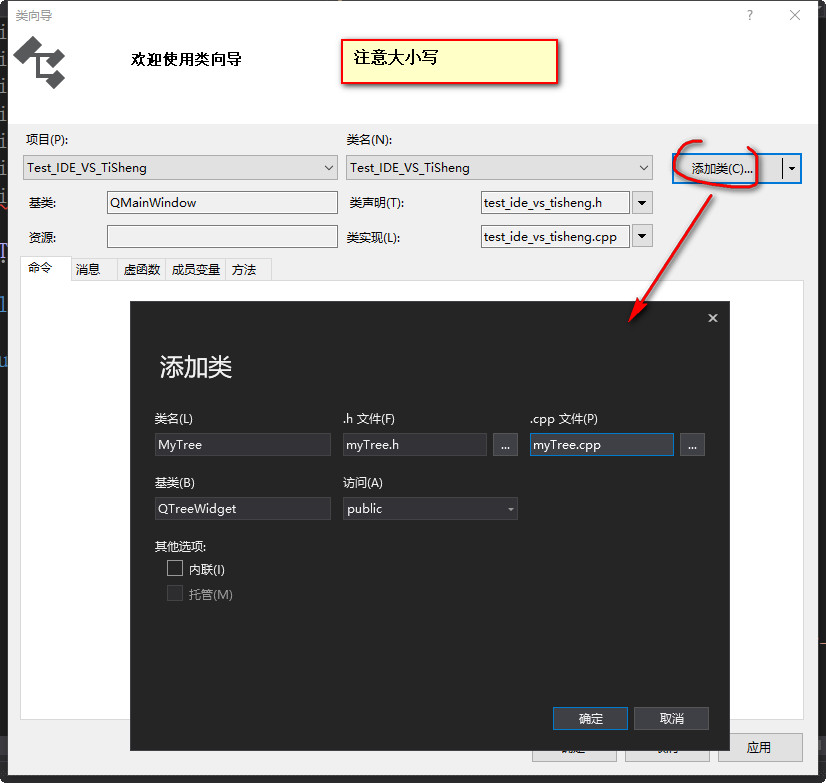
E:

 

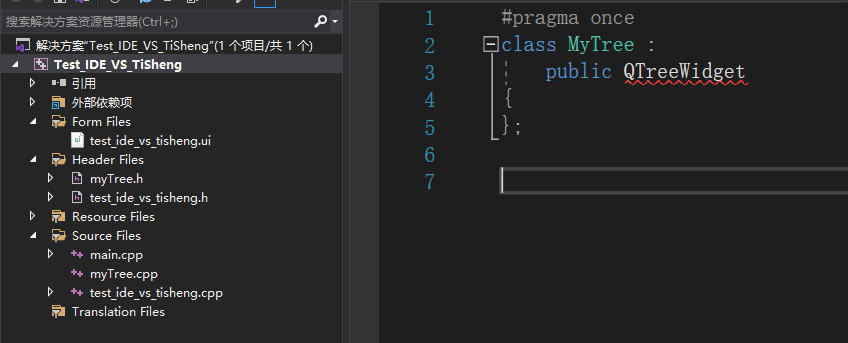
F:

  Add header file #include < QTreeWidget > manually, otherwise QTreeWidget cannot be recognized

××

//This file is myTree.h
#pragma once
#include<QTreeWidget>
class MyTree :
    public QTreeWidget
{
};

G: Add constructor for MyTree

//This file is myTree.h
#pragma once
#include<QTreeWidget>
class MyTree :
    public QTreeWidget
{
public:
    MyTree(QWidget* parent = 0);

};

//The file is: myTree.cpp
#include "myTree.h"

MyTree::MyTree(QWidget* parent)//Constructor
{

}

At this point, the program can be compiled and run

Step 7: then, we can further handle the promoted, that is, derived classes

(class MyTree : public QTreeWidget)

××××

A: Add a member function declaration in the header file

//This file is myTree.h
#pragma once
#include<QTreeWidget>
class MyTree :
    public QTreeWidget
{
public:
    MyTree(QWidget* parent = 0);
    void test();//Declare in myTree.h
};

B: The member function is implemented in the source file

//The file is: myTree.cpp
#include "myTree.h"
#include <QMessageBox>
MyTree::MyTree(QWidget* parent)//Constructor
{
	 
}

void MyTree::test()
{
	QMessageBox::warning(0, "test", "test");
}

C: Add a call to test_ide_vs_tisheng.cpp

#include "test_ide_vs_tisheng.h"
#include "myTree.h"
Test_IDE_VS_TiSheng::Test_IDE_VS_TiSheng(QWidget *parent)
    : QMainWindow(parent)
{
    ui.setupUi(this);
    ui.treeWidget->test();//Call the function of the myTree class

}

Step 8: so far, we have finally realized the promotion and control in VS. this blog should be the most detailed in the full text. The source code is as follows

https://download.csdn.net/download/wenluderen/25860410