Trees have some simple basics that you must know

• Tree is a nonlinear data structure, which is defined recursively
• Node degree: the number of subtrees contained in a tree is called node degree
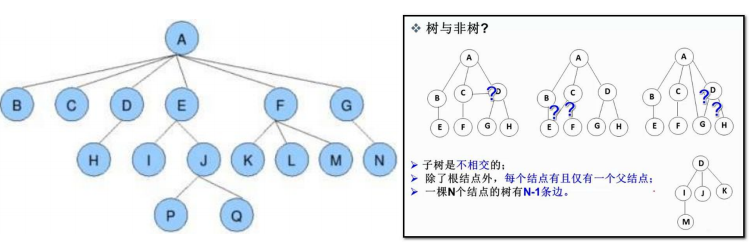  As shown in the figure, the degree of node A is 6, and the degree of node B is 0
• Tree degree: the degree of the largest node of a tree is called the degree of the tree, as shown in the figure above: the degree of the tree is 6
• Leaf node: a node with a degree of 0 is called a leaf node
• Parent node (parent node): if A node contains child nodes, this node is called the parent node of its child nodes; As shown in the figure above, A is the parent node of B
• Root node: A node in A tree without parent nodes; As shown in the figure above: A
• Node hierarchy: defined from the root, the root is the first layer, and the child node of the root is the second layer, and so on;
• Height of tree: the maximum level of nodes in the tree; As shown in the figure above: the height of the tree is 4

Application of tree

Types of binary trees

In the process of solving problems, binary trees have two main forms: full binary trees and complete binary trees

• Full binary tree
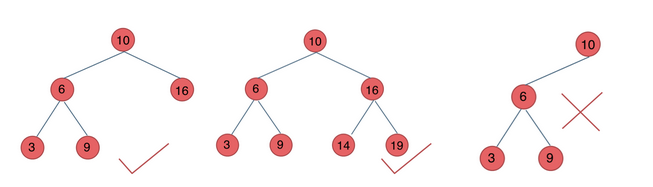
  Full binary tree: if a binary tree has only nodes with degree 0 and degree 2, and the nodes with degree 0 are on the same layer, the binary tree is a full binary tree.
  
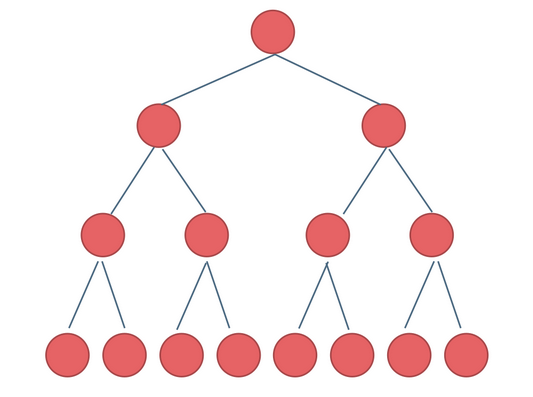
  This binary tree is a full binary tree, or a binary tree with a depth of K and 2^k-1 nodes

• Complete binary tree

What is a complete binary tree?

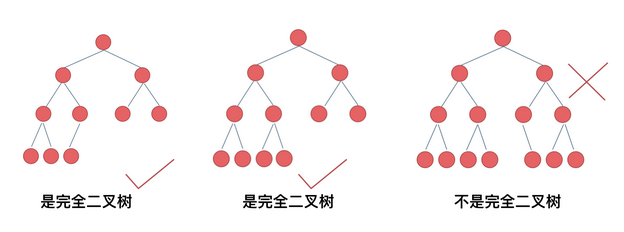
The definition of a complete binary tree is as follows: in a complete binary tree, except that the bottom node may not be filled, the number of nodes in each layer reaches the maximum, and the nodes in the lowest layer are concentrated in several positions on the leftmost side of the layer. If the bottom layer is layer h, the layer contains 1~ 2^h -1 nodes.
The priority queue written in the previous article is a heap, which is a complete binary tree, and ensures the sequential relationship between parent and child nodes.

Search Binary Tree

The trees described above have no numerical values, while the binary search tree has numerical values. The binary search tree is an ordered tree

• If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node
• If its right subtree is not empty, the value of all nodes on the right subtree is greater than that of its root node
• Its left and right subtrees are also binary sort trees
  

Balanced binary search tree (AVL)

Nature: it is an empty tree or the absolute value of the height difference between its left and right subtrees does not exceed 1, and both the left and right subtrees are a balanced binary tree.

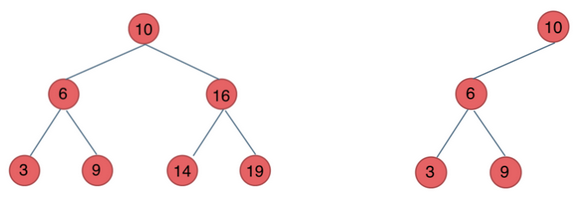
We mentioned the binary search tree earlier. We know that the characteristics of the binary search tree are convenient for us to find, insert, delete and other operations. Its time complexity is O (logn). However, if we encounter the worst situation, such as the following tree

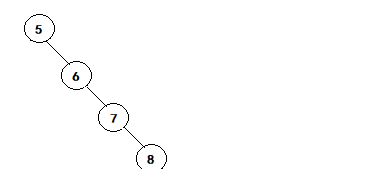In fact, this tree has degenerated into a linked list, but it is still a binary search tree. We construct a binary search tree in the order of 5, 6, 7 and 8, as shown in the figure above. The insertion time complexity becomes O(n). The reason for this bad situation is that the tree is extremely unbalanced, and the weight of the right tree is much greater than that of the left tree. Therefore, we propose a structure called balanced binary search tree, also known as AVL tree

We use our familiar programming language to write algorithms. We must know how to implement the bottom layer of common containers. The most basic ones are map, set, etc., which is helpful for us to analyze the performance of our own code

Storage method of binary tree

The storage structure of binary tree is divided into sequential storage and chain storage similar to linked list.
The chain storage of binary tree is referenced by nodes one by one. The common representation is binary representation, as follows:

// Child representation
class Node {
 int val; // Data domain
 Node left; // The reference of the left child often represents the whole left subtree with the left child as the root
 Node right; // The reference of the right child often represents the whole right subtree with the right child as the root
}

The sequential storage method is shown in the figure:

If the following table of the parent node array is i, its left child is i * 2 + 1 and its right child is i * 2 + 2

Traversal of binary tree

There are two main traversal methods for binary trees:
1: Depth first traversal: go deep first, and then go back when you encounter a leaf node.
2: Breadth first traversal: traversal layer by layer.

I have summarized the previous, middle and subsequent traversal here: The first, middle and last order traversal of binary tree, which can be understood in seconds

In the last article, I wrote some related contents of stack and queue, and stack is actually an implementation structure of recursion, that is to say, the logic of pre -, middle - and post order traversal can be realized in a non recursive way with the help of stack.
The implementation of breadth first traversal generally uses queue, which is also determined by the characteristics of queue first in first out, because the structure of first in first out is required to traverse the binary tree layer by layer.

//Binary tree node definition
public class TreeNode {
    int val;
  	TreeNode left;
  	TreeNode right;
  	TreeNode() {}
  	TreeNode(int val) { this.val = val; }
  	TreeNode(int val, TreeNode left, TreeNode right) {
    		this.val = val;
    		this.left = left;
    		this.right = right;
  	}
}

Recursive traversal of binary tree

• Preorder traversal of binary tree (leetcode: 144. Preorder traversal of binary tree)

//Defines the head node of a binary tree
public class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {};
    TreeNode(int val){ this.val=val;}
    TreeNode(int val,TreeNode left,TreeNode right){
        this.val=val;
this.left=left;
this.right=right;
    } 

}
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
ArrayList<Integer> result=new ArrayList<>();
preOrder(root,result);
return result;
    }
    void preOrder(TreeNode root,ArrayList result){
        if(root==null){
            return;
        }
        result.add(root.val);
        preOrder(root.left,result);
        preOrder(root.right,result);
    }
}

• Middle order traversal of binary tree (leetcode: 94. Middle order traversal of binary tree)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
ArrayList<Integer> result=new ArrayList<>();
inOrder(root,result);
return result;
    }
    void inOrder(TreeNode root,ArrayList result){
        if(root==null){
            return;
        }
         inOrder(root.left,result);
         result.add(root.val);//Pay attention to this sentence
         inOrder(root.right,result);
    }
}

• Postorder traversal of binary tree (145. Postorder traversal of binary tree)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
ArrayList<Integer> result=new ArrayList<>();
postOrder(root,result);
return result;
    }
    void postOrder(TreeNode root,ArrayList result){
     if(root==null){
         return;
     }
     postOrder(root.left,result);
     postOrder(root.right,result);
     result.add(root.val);
    }
}

To be continued,,,,