Write in front
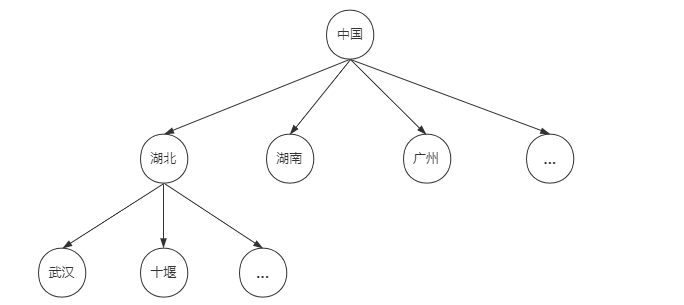
The linked list, stack and queue mentioned earlier are linear storage structures, which are one-to-one relationships. Tree is a data structure with one to many relationship. For example, we often say that a class diagram in Wuhan, Hubei Province and Changsha, Hunan Province is similar to an inverted tree.
What is a tree
Tree is a kind of data structure, which is a finite set with hierarchical relationship composed of n nodes.

Basic terms of trees
Node: every data element in the tree is A node (A, B...)
Degree of node: number of subtrees of node (subtrees of A are B and C)
Degree of tree: the maximum degree of all nodes in the tree (the degrees of tree A and tree C are both 2)
Leaf node: node with degree 0 (D, E, F)
Node hierarchy: starting from the root of the tree, the layer where the tree root is located is the first layer, and the layer where the root's child nodes are located is the second layer (A first layer, BC second layer)
Height of tree: the maximum level of all nodes in the tree is the height of the tree
Ordered tree and unordered tree: the subtree can be divided into left and right order (for example, the one on the left is less than the one on the right), otherwise it is an unordered tree
Characteristics of trees
- Subtrees are disjoint
- In addition to the root node, each node has one and only one parent node
- A tree composed of N nodes has only N-1 edges
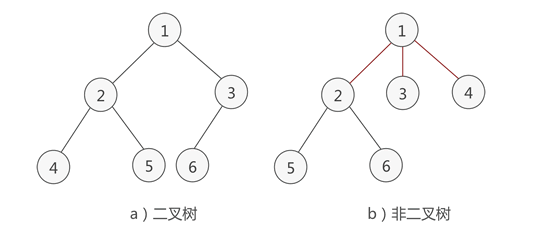
What is a binary tree
An ordered tree in which the degree of nodes in the tree does not exceed 2.
Characteristics of binary tree:
-
In the binary tree, the maximum number of nodes in layer I is 2i-1
-
A binary tree with a depth of K can have up to 2k-1 nodes
-
For any binary tree, if the number of terminal nodes (number of leaf nodes) is n0 and the number of nodes with degree 2 is n2, then n0=n2+1,
That is, node n0 with degree 0 is always one more than node n2 with degree 2.

It is proved that there are n0 nodes with degree 0, n1 nodes with degree 1 and n2 nodes with degree 2, a total of n nodes,
Because the degree of all nodes of the binary tree is not greater than 2, so:
n = n0 + n1 + n2 ①
In addition, since nodes with 0 degrees have no children, nodes with 1 degree have one child, and nodes with 2 degrees have two children, the total number of children is:
0 * n0 + 1 * n1 + 2 * n2. In addition, the root node (the node of the first layer) is not the child of any node, so
Total nodes = total number of children + root node, i.e
n = n1 + 2n2 + 1 ②
② - ① simplification
n0 = n2 + 1
Full binary tree
In a binary tree, except for leaf nodes, the degree of each node is 2, then the binary tree is a full binary tree.
The depth of a full binary tree with n nodes is log2(n+1)

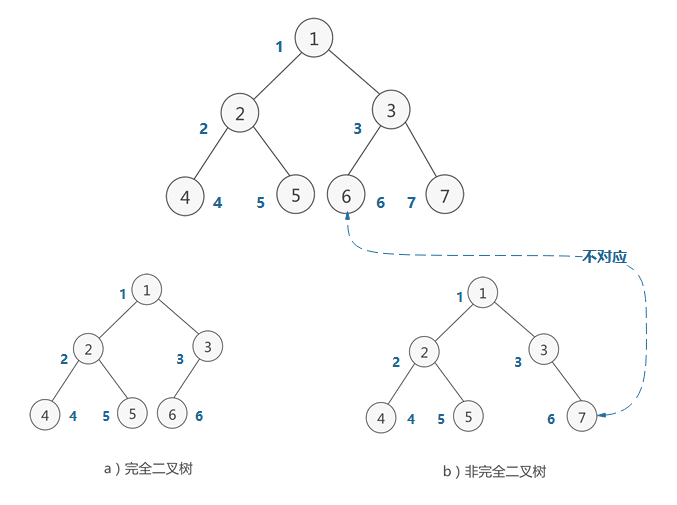
Complete binary tree
If the nodes of the full binary tree are numbered, the Convention number starts from the root node, from top to bottom, from left to right. A binary tree with depth k and n nodes is called a complete binary tree if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth k.
Features: leaf nodes can only appear in the lowest layer and sub lower layer, and the leaf nodes at the lowest layer are concentrated on the left of the tree. It should be noted that a full binary tree must be a complete binary tree, and a complete binary tree is not necessarily a full binary tree.
Huffman tree (optimal binary tree)
If a binary tree is given as follows:

Path: the path from one node to another in a tree is called a path. As shown in the figure above, the path from the root node to a.
Path length: in a path, the path length is increased by 1 for each node. As shown in the figure above, the path length from the root node to node c is 3.
Node weight: each node is given a new value. If a's right is 7, b's right is 5.
Weighted road strength length of a node: the product of the path length from the root node to the node and the weight of the node. For example, the weighted path length of b is 2 * 5 = 10.
Weighted path length of tree: the sum of weighted path lengths of all leaf nodes in the tree. Usually referred to as "WPL". As shown in the figure, the weighted path length of this tree is: WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
What is Huffman tree
Construct a binary tree (each node is a leaf node and has its own weight). The weighted path length of the tree reaches the minimum, which is called the optimal binary tree, also known as Huffman tree
Coding problem
Scenario: a given string contains 58 characters and is composed of the following 7 characters: A, B, C, D, e, F and g. the frequency of these 7 characters is different. How to encode these 7 characters and how to encode the string to minimize the encoding storage space of the string?

If standard equal length ASCII encoding is used: 58 × 8 = 464 bits
Coding with binary tree
If you use 0 and 1 to represent the left and right branches, take out the above four characters with the highest frequency, and you can get the following tree:

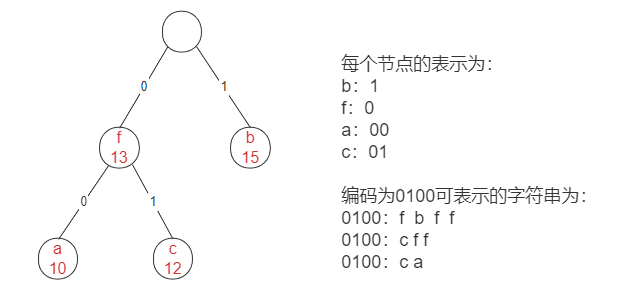
As can be seen from the above figure, there are three possible situations for characters represented by 0100. Therefore, the distribution of the above nodes is ambiguous. How to avoid ambiguity? Just make each node a leaf node.
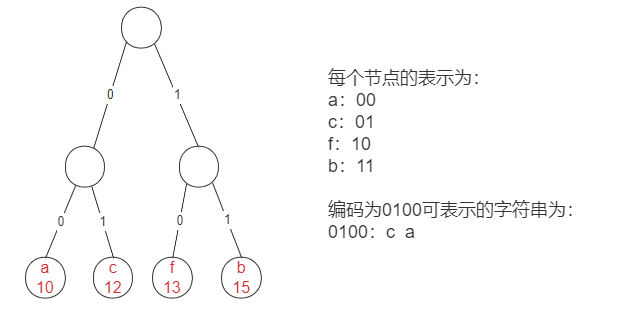
Huffman tree diagram construction
In the above way, we combine the above characters in pairs according to frequency, and they are leaf nodes. The final structure diagram is as follows:
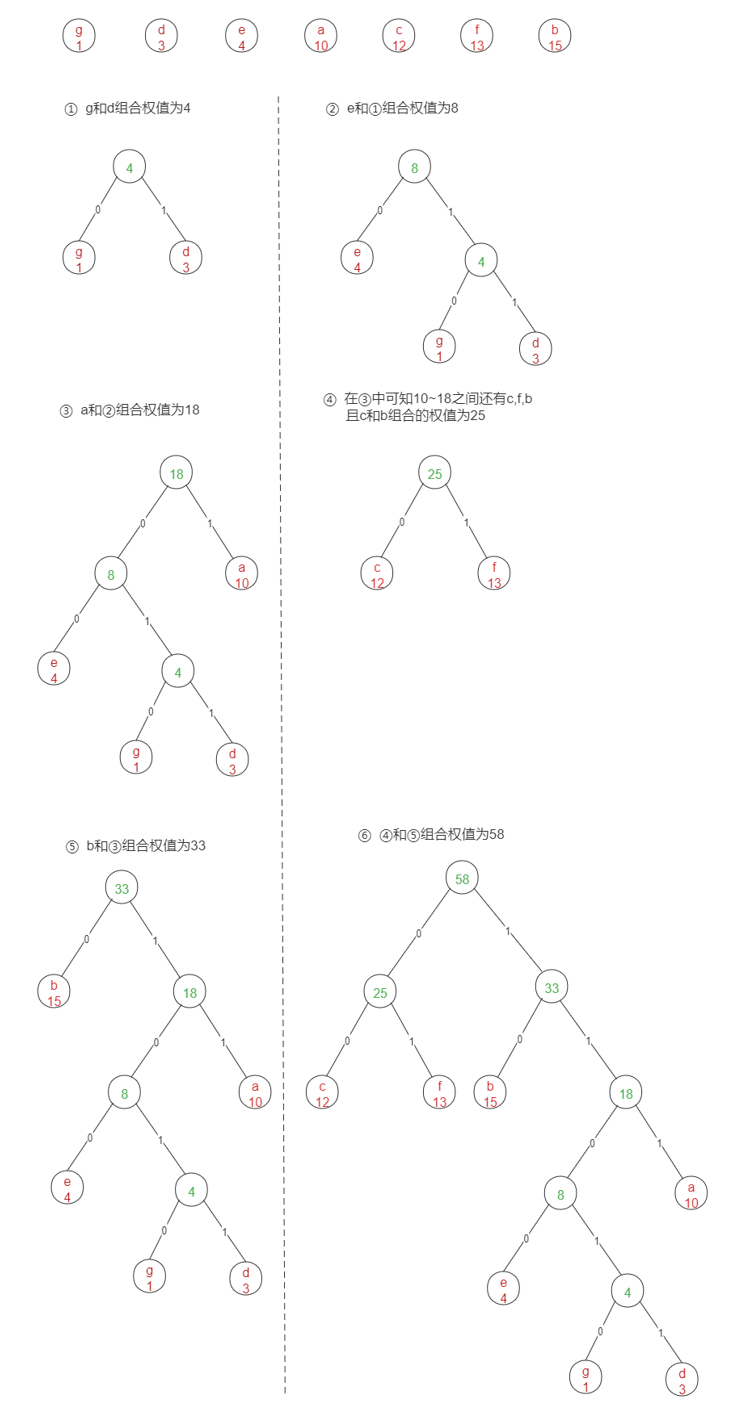
Therefore, we found that each node is a leaf node, and the last code of the character is:

Therefore, the encoding length is:
10x3 + 15x2 + 12x2 + 3x5 + 4x4 + 13x2 + 1x5 = 146 bits
Code construction
public class HuffmanTree {
//node
public static class Node<E> {
//Data, such as a,b,c,d...
E data;
//weight
int weight;
//Left child node
Node leftChild;
//you child node
Node rightChild;
public Node(E data, int weight) {
this.data = data;
this.weight = weight;
}
public String toString() {
return "Node[" + weight + ",data=" + data + "]";
}
}
public static Node createHuffmanTree(List<Node> nodeList) {
//When the node is greater than 1
while (nodeList.size() > 1) {
//First sort the list according to the weight
sort(nodeList);
//After sorting, the first node is the node with the smallest weight, and the second node is the node with the second smallest weight
Node left = nodeList.get(0);
Node right = nodeList.get(1);
//Generate a new parent node, similar to step 1, but the parent node has no data and only weights
Node<Node> parent = new Node<>(null, left.weight + right.weight);
//Child and parent node links
parent.leftChild = left;
parent.rightChild = right;
//Delete the smallest node
nodeList.remove(0);
//Delete the second smallest
nodeList.remove(0);
//Add to list
nodeList.add(parent);
}
//Finally, a tree is returned to the root node
return nodeList.get(0);
}
/**
* Fake sort
*
* @param nodeList
*/
public static void sort(List<Node> nodeList) {
if (nodeList.size() <= 1) {
return;
}
for (int i = 0; i < nodeList.size(); i++) {
for (int j = 0; j < nodeList.size() - 1; j++) {
//If the preceding number is greater than the following number, it will be exchanged
if (nodeList.get(j + 1).weight < nodeList.get(j).weight) {
Node temp = nodeList.get(j + 1);
nodeList.set(j + 1, nodeList.get(j));
nodeList.set(j, temp);
}
}
}
}
/**
* Print Huffman tree from left to right
* That is, the left node of the child node is printed first from the root node, and the right node is printed
* @param root Root node tree
*/
public static void printTree(Node root) {
if (root.leftChild != null) {
System.out.println("Left child node:" + root.leftChild);
printTree(root.leftChild);
}
if (root.rightChild != null) {
System.out.println("Right child node:" + root.rightChild);
printTree(root.rightChild);
}
}
//test
public static void main(String[] args) {
List<Node> nodes = new ArrayList<Node>();
//Add nodes to the list
nodes.add(new Node("a", 10));
nodes.add(new Node("b", 15));
nodes.add(new Node("c", 12));
nodes.add(new Node("d", 3));
nodes.add(new Node("e", 4));
nodes.add(new Node("f", 13));
nodes.add(new Node("g", 1));
Node root = createHuffmanTree(nodes);
printTree(root);
}
}
test result
Left child node: Node[25,data=null] Left child node: Node[12,data=c] Right child node: Node[13,data=f] Right child node: Node[33,data=null] Left child node: Node[15,data=b] Right child node: Node[18,data=null] Left child node: Node[8,data=null] Left child node: Node[4,data=e] Right child node: Node[4,data=null] Left child node: Node[1,data=g] Right child node: Node[3,data=d] Right child node: Node[10,data=a]
summary
This chapter is mainly about the basic concept of tree and understanding the characteristics of common trees. Later, we will continue to talk about binary sorting tree and binary balanced tree. The data structure is relatively boring, but we will gain if we stick to it. It will greatly improve both the algorithm and the source code.