1, What is the life cycle of vue?
The process from creation to use and finally destruction of Vue instances or components is called Vue's life cycle function, which can also be understood as a function that Vue instances will automatically execute at a certain point in time.
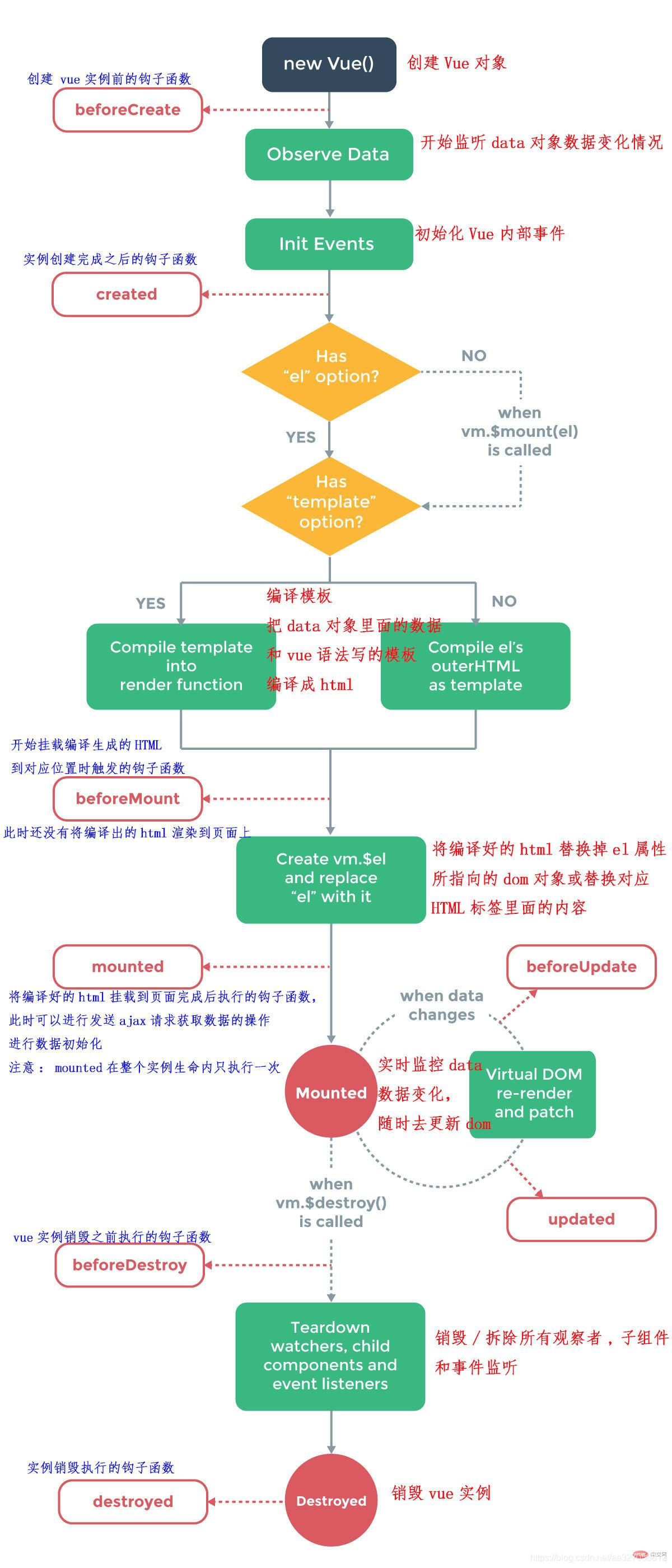
The above figure is transferred from: https://blog.csdn.net/aa327056812/article/details/113848734
2, What are the life cycle functions of vue and what are their functions?
1. Before creating an instance: BeforeCreate function:
Triggered after the Vue instance is created. This cannot be used at this time. Neither the data methods method in data nor the events in watch can be obtained.
2. After creating an instance: the Created function:
The instance has been created and the instance object has been completed. At this time, you can access the data in data, the methods in methods and the events in watch.
Although the data can be used or changed at this time, the updated function will not be triggered when the data is synchronously modified here. Generally, the initial data can be obtained here.
3. Before template rendering: beforeMount:
During this period, the template is compiled, but there is no element mount, and the DOM cannot be obtained. In this function, the virtual DOM has been created and will be rendered.
You can also modify the data here without triggering updated, which is the last chance to change the data before rendering.
4. After rendering: mounted:
After mounting, the real dom is rendered, and then the mounted hook function is executed. At this time, the component has appeared in the page, the data and the real dom have been processed, and some operations on the dom can be carried out at this time.
5. Before updating data: beforeUpdate
After the data of the component or instance changes, it will execute beforeUpdate immediately, that is, the data is updated, but the data in the dom corresponding to the component in vue has not changed, so it is called before component update.
6. After updating the data: updated
After the component update is completed, the components in Vue already correspond to the data in the dom. You can continue to operate the updated dom.
7. Before destroying an instance: beforeDestroy
When the destroy () method is called in a certain way, beforeDestroy will be executed immediately. Generally, some aftercare work will be done here, such as clearing timers and clearing non instruction bound events. At this time, the instance can still be used.
8. After instance destruction: destroyed
It is executed after the Vue instance is destroyed. After the Vue instance is destroyed, the dom element still exists, but the data is bound in both directions. The function of Vue is gone, and the dom is only an empty shell.
3, Vue lifecycle function implementation
The following code shows the changes in each period of Vue's complete life cycle.
View the status in the Console after running
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Document</title>
<script src="./js/vue.js"></script>
</head>
<body>
<div id="app">
<p>{{ message }}</p>
<input type="button" @click="change" value="Update data" />
<input type="button" @click="destroy" value="Destroy" />
</div>
<script type="text/javascript">
var vm = new Vue({
el: '#app',
data: {
message : "Welcome Vue"
},
methods:{
change() {
this.message = 'Datura is me';
},
destroy() {
vm.$destroy();
}
},
beforeCreate: function () {
console.group('beforeCreate Pre creation status===============>');
console.log("%c%s", "color:red","el : " + this.$el); //undefined
console.log("%c%s", "color:red","data : " + this.$data); //undefined
console.log("%c%s", "color:red","message: " + this.message);//undefined
},
created: function () {
console.group('created Create complete status===============>');
console.log("%c%s", "color:red","el : " + this.$el); //undefined
console.log("%c%s", "color:green","data : " + this.$data); //[object] = > initialized
console.log("%c%s", "color:green","message: " + this.message); //Welcome Vue = > initialized
},
beforeMount: function () {
console.group('beforeMount Pre mount status===============>');
console.log("%c%s", "color:green","el : " + (this.$el)); //Has been initialized
console.log(this.$el); // Currently hanging element
console.log("%c%s", "color:green","data : " + this.$data); //Has been initialized
console.log("%c%s", "color:green","message: " + this.message); //Has been initialized
},
mounted: function () {
console.group('mounted Mount end status===============>');
console.log("%c%s", "color:green","el : " + this.$el); //Has been initialized
console.log(this.$el);
console.log("%c%s", "color:green","data : " + this.$data); //Has been initialized
console.log("%c%s", "color:green","message: " + this.message); //Has been initialized
},
beforeUpdate: function () {
alert("Status before update");
console.group('beforeUpdate Status before update===============>'); //This refers to the page before rendering new data
console.log("%c%s", "color:green","el : " + this.$el);
console.log(this.$el);
console.log("%c%s", "color:green","data : " + this.$data);
console.log("%c%s", "color:green","message: " + this.message);
alert("Status before update 2");
},
updated: function () {
console.group('updated Update completion status===============>');
console.log("%c%s", "color:green","el : " + this.$el);
console.log(this.$el);
console.log("%c%s", "color:green","data : " + this.$data);
console.log("%c%s", "color:green","message: " + this.message);
},
beforeDestroy: function () {
console.group('beforeDestroy Status before destruction===============>');
console.log("%c%s", "color:red","el : " + this.$el);
console.log(this.$el);
console.log("%c%s", "color:red","data : " + this.$data);
console.log("%c%s", "color:red","message: " + this.message);
},
destroyed: function () {
console.group('destroyed Destroy complete status===============>');
console.log("%c%s", "color:red","el : " + this.$el);
console.log(this.$el);
console.log("%c%s", "color:red","data : " + this.$data);
console.log("%c%s", "color:red","message: " + this.message)
}
})
</script>
</body>
</html>
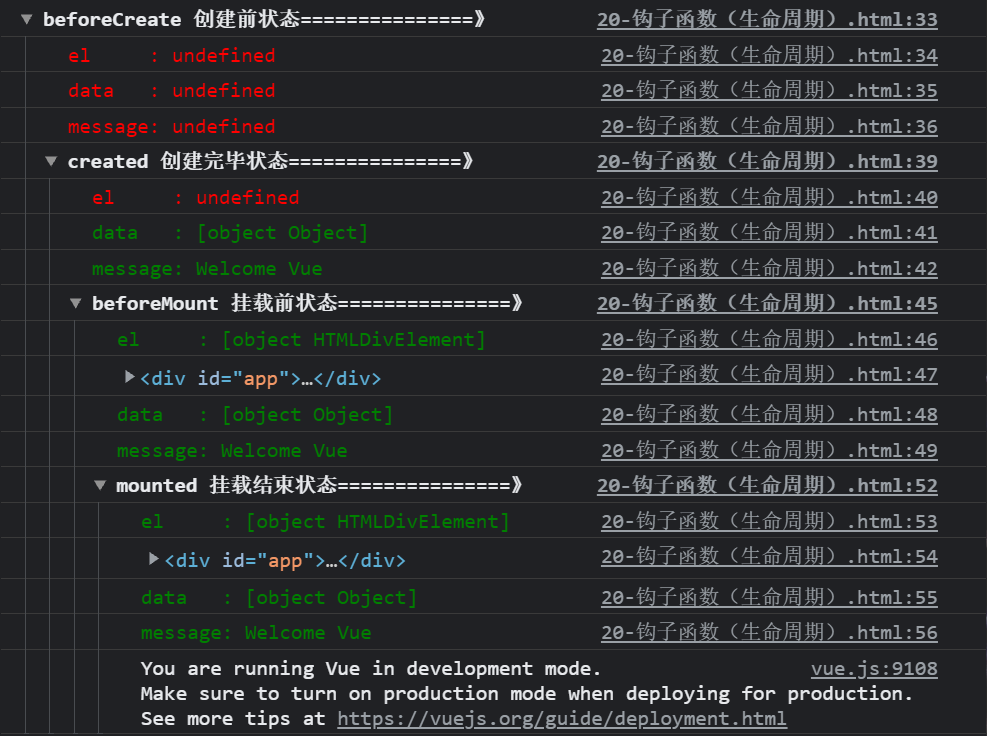
Figure 1
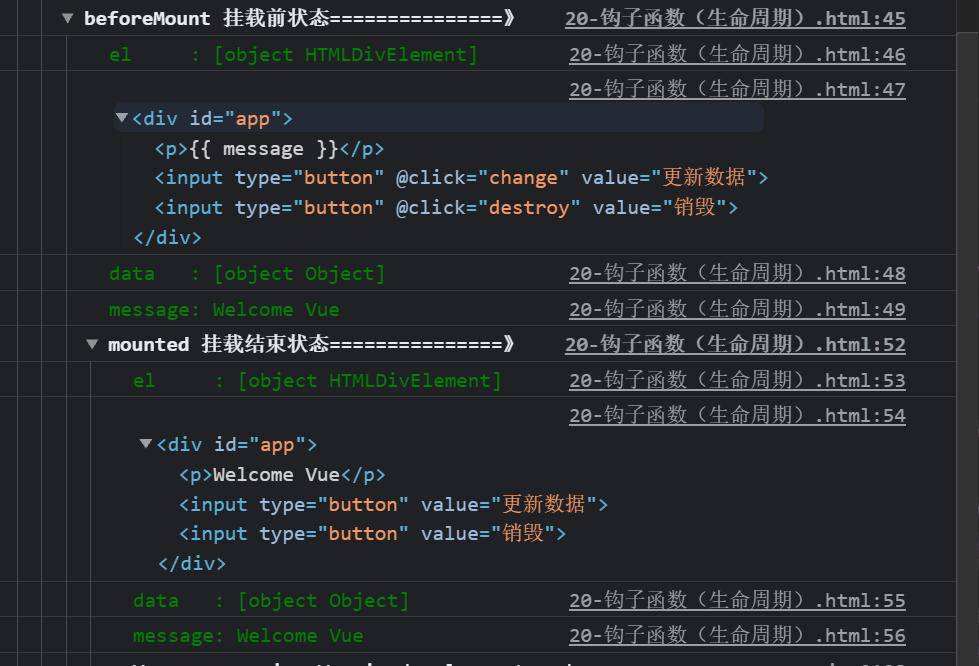
Figure 2
1.create and mounted
See Figure 1
beforeCreated: el and data are not initialized.
created: data initialization is completed, but el not.
beforeMount: the initialization of el and data is completed.
Mounted: mounted.
See Figure 2
We also found that in the beforeMount stage, el is still {{message}}. Here, the virtual Dom technology is applied, and the value will be rendered when mounted later.
2.update
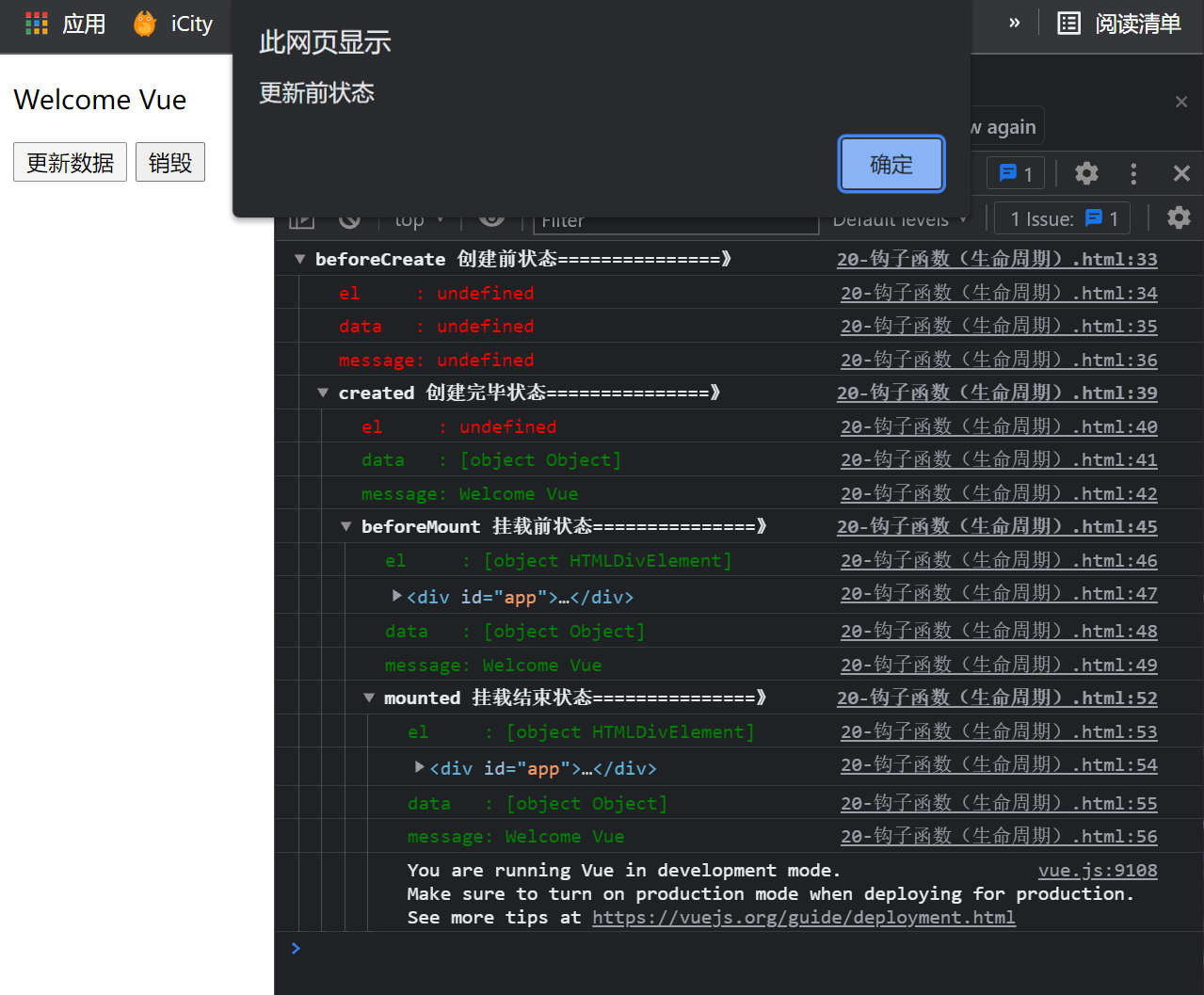
Figure 3
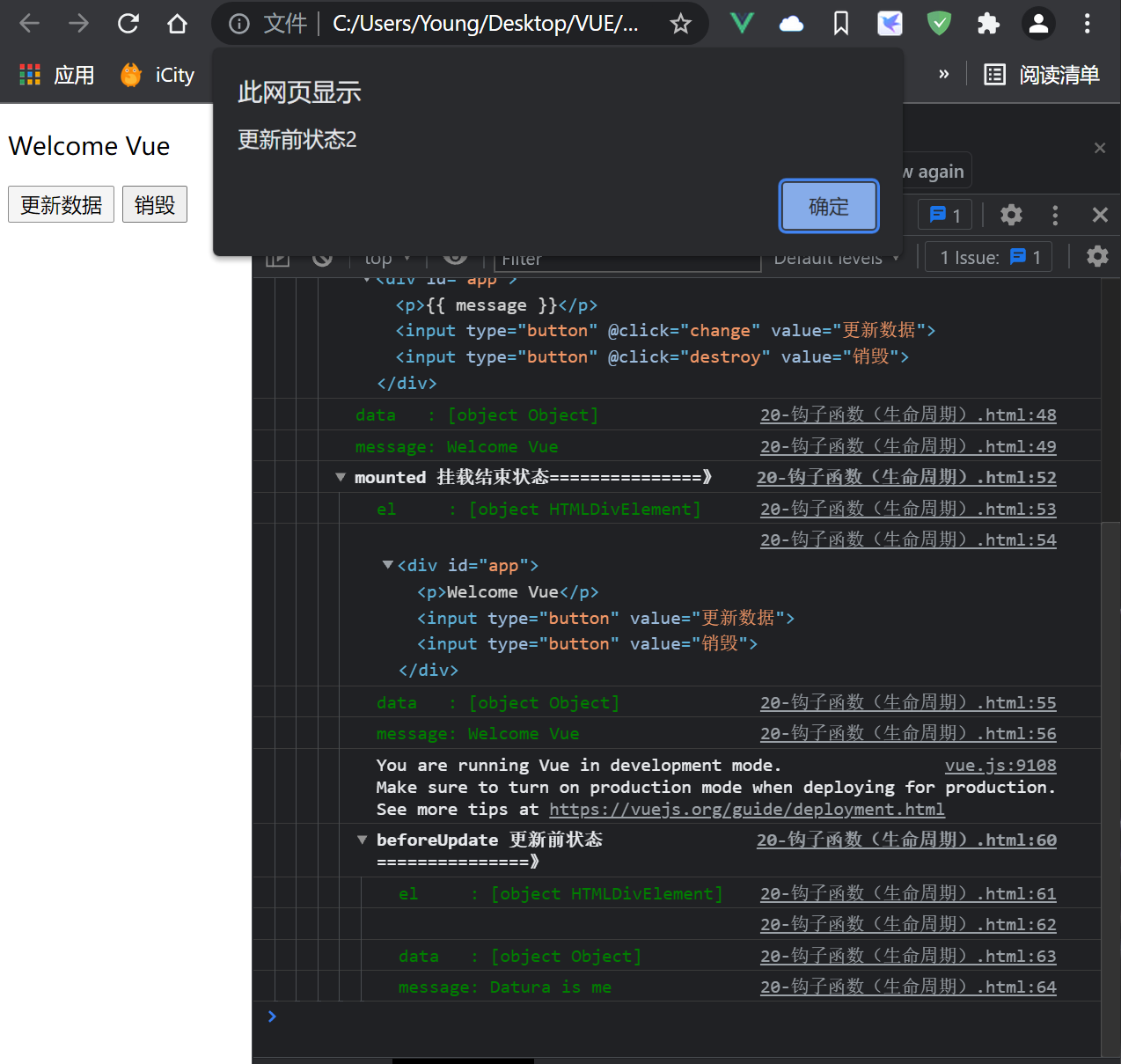
Figure 4
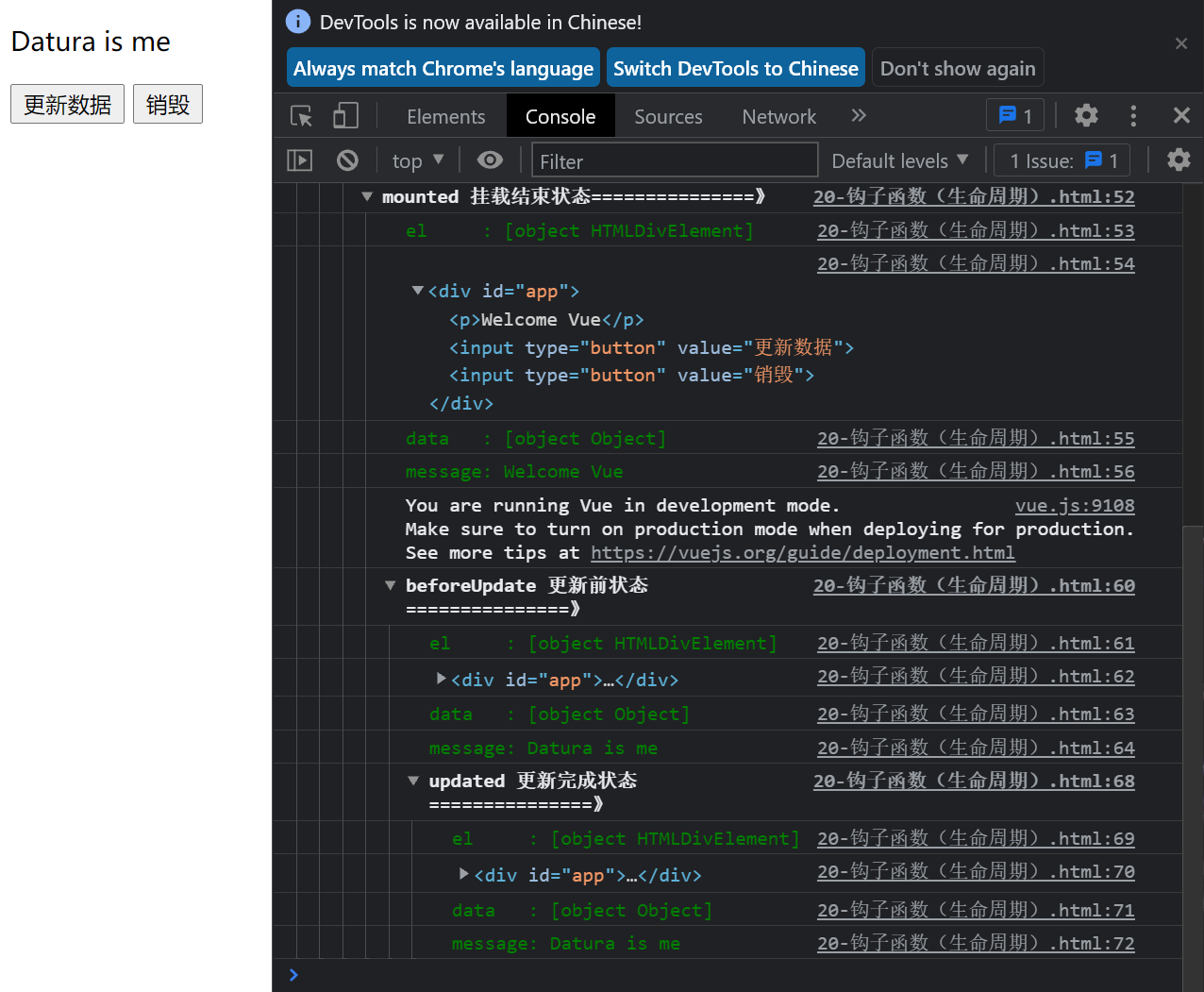
Figure 5
See Figure 4
After clicking the update button, the beforeUpdate event is triggered. At this time, the data of the data layer does not change, but the data of the view layer changes.
See Figure 5
Here, the text in the page has changed, indicating that the Updated event has occurred.
3.destroy
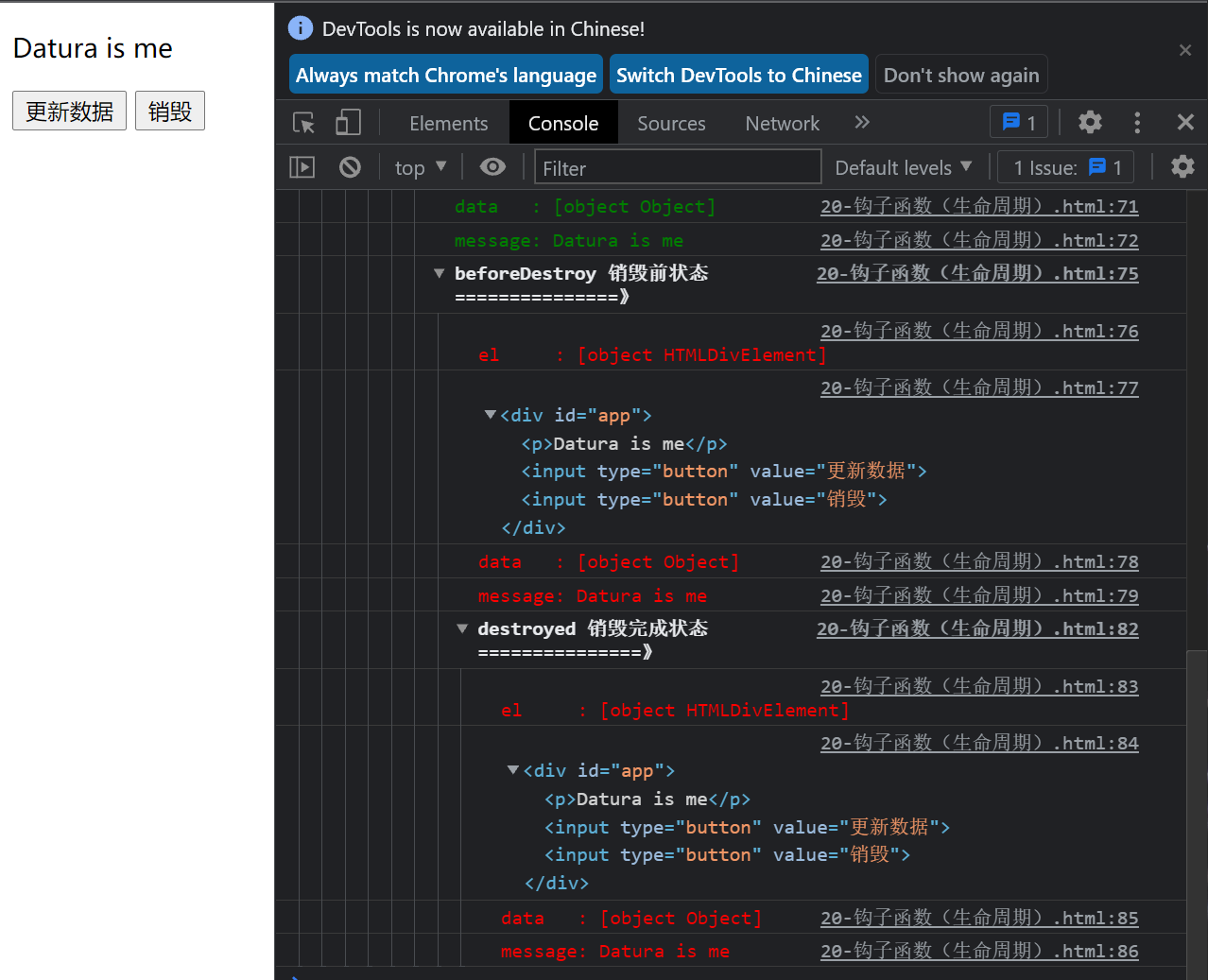
Figure 6
See Figure 6
After the destruction is completed, we change the value of message, and vue will no longer respond. But the original dom element still exists.