A basic union search set

There are only two operations for the basic union query set, one is to find ancestors, and the other is to merge

int find(int x)
{
    if(x==pre[x]) return x;
    else return pre[x]=find(pre[x]);
}
void join(int x,int y)
{
    pre[find(x)]=find(y);
}

Two weighted union search set

  for weighted concurrent search set, it can maintain certain other relationships, such as distance, on our basis. Here we take Hangzhou Electric ~ HDUyyds as an example How Many Answers Are Wrong For example, in this topic, each sentence gives you the sum of the number between each point, and you have to judge which of these sentences are wrong and output the number of errors

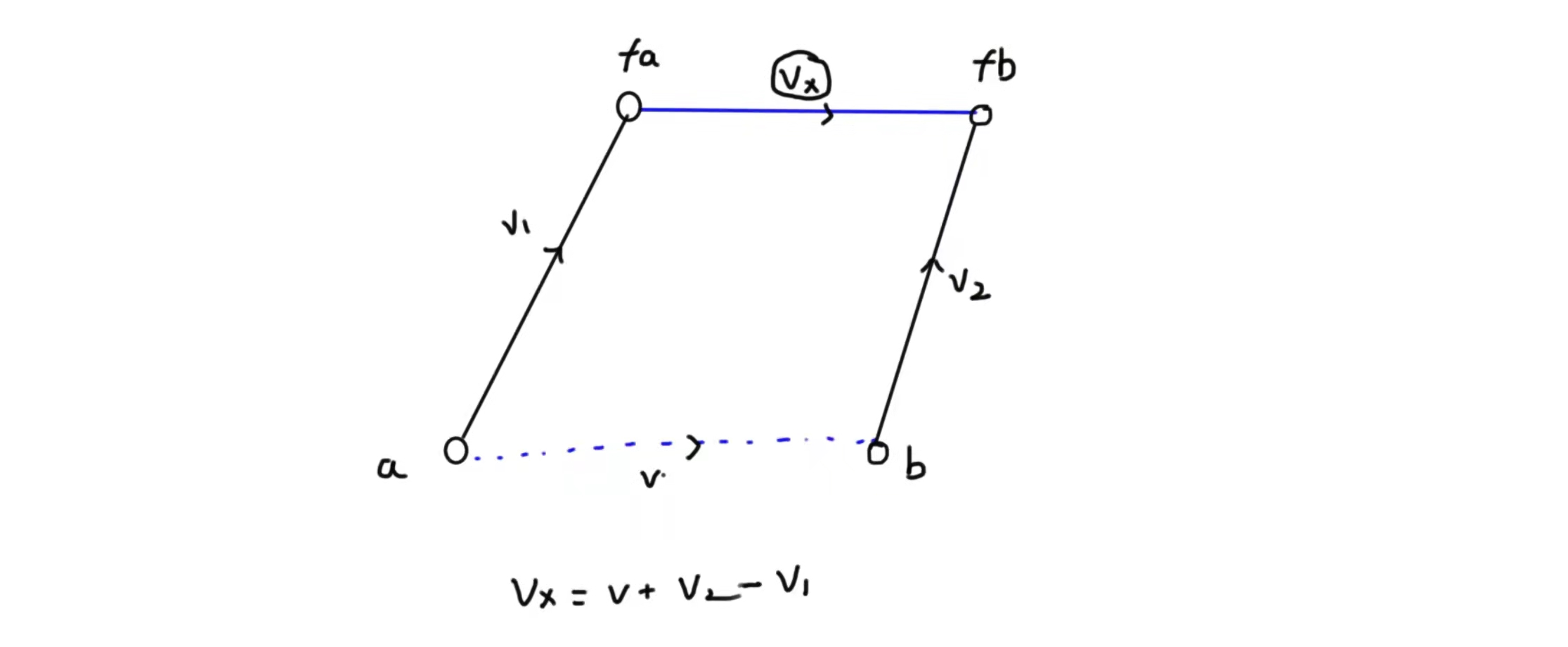
  for the left and right boundaries given in each sentence, we can regard them as a point, and the sum of this interval is the weight above this edge, and we can convert this weight into a relative value to get the value of a pile of points about a point. After merging the points, we can get the relative value between the two points

  taking the above points a and b as an example, we can get that the fathers of a and b are fa and fb respectively, and the weight relationship between a and b is v. at this time, we combine the branch represented by a into our branch quotient of b. at this time, we can get the equation relationship v 1 + v x = v + v 2 v_{1} +v_{x} = v+v_2 v1 + vx = v+v2, so we update the weight of fa about fb

 code is as below

#include <iostream>
#define N 200005
using namespace std;
int f[N],value[N];
inline int find(int x) {
    if(x == f[x]) return x;
    else {
        int a = f[x];
        f[x] = find(f[x]);
        value[x] = value[x] + value[a];
        return f[x];
    }
}
int ans = 0;
int main() {
    int n,m;
    scanf ("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) f[i] = i;
    int x,y,z;
    for (int i = 1;i <= m;i++) {
        scanf("%d%d%d",&x,&y,&z);
        int fl = find(x),fr = find(y);
        if(fr == fl) {
            if(value[x] - value[y] != z) ans++;
            else {
                f[fl] = fr;
                value[fl] = -value[x] + value[y] + z;
            }
        }
    }
    printf("%d",ans);
}

Three kinds of parallel search set

  category and search set actually means that all elements belong to a certain category, and then judge whether the result is true according to the logical relationship between each point, Category query template

  category merge query set is a branch of weight merge query set, but it can not be completely regarded as yes. Let me introduce two ways to write category merge query set

A writing method based on weighted parallel search set

#include <iostream>
using namespace std;
int f[100000],re[100000]; // re represents the corresponding relationship of each point, 0,1,2, 0 represents the same kind, 1 represents the predator-prey relationship, and 2 represents the predator-prey relationship
int n,m,ans;
int find(int a)
{
   int fa=f[a];
   if (a!=fa) {
       f[a]=find(fa);
       re[a]=(re[a]+re[fa])%3;
       return f[a];
   }
   else return fa;
}
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++) f[i] = i;
    for (int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&z,&x,&y);
        if ((x>n||y>n)||(z==2&&x==y)) {   //Two special cases
            ans++; continue;
        }
       if (z==1)
       {
           int f1=find(x),f2=find(y);
           if (f1==f2&&re[x]!=re[y])
           {
               ans++; continue;
           }
           else if(f1!=f2)
           {
               f[f1]=f2; re[f1]=(3-re[x]+re[y])%3;
             // Merge and query sets. They are of the same type, so they should be equal
           }
       }
       else {
           int f1=find(x),f2=find(y);
           if (f1==f2)
           {
             // If the merger has already been made, then if it is not a predator-prey relationship, it is an error
               int rela=(re[x]-re[y]+3)%3;
               if (rela!=1) {
                   ans++; continue;
               }
           }
           else {
               f[f1]=f2; re[f1]=(3-re[x]+re[y]+1)%3;
             // The species are different and there is a predation relationship, so 1 should be added
           }
       }
   }
    printf("%d\n",ans);
    return 0;
}

II. Writing method of multi open point space

  use i i i represents itself, i + n i+n i+n represents the prey, i + 2 ∗ n i+2*n i+2 * n indicates the strong prey

#include <iostream>
#define N 1010
using namespace std;
int f[N*3];
inline int find(int x){
    if(x == f[x]) return x;
    else{
        return f[x] = find(f[x]);
    }
}
int main() {
    int n,m,ans = 0;
    scanf("%d%d",&n,&m);
    for (int i = 1;i <= 3*n;i++) f[i] = i;
    for (int i = 1;i <= m;i++) {
        int x,y,z;
        scanf("%d%d%d",&z,&x,&y);
        if(x > n|| y > n||(z == 2&&x == y)) {ans++;continue;}
        if(z == 1) {
            if (find(x+n) == find(y) || find(y+n) == find(x)) {ans++;}
            else  {
                f[find(x)] = find(y);
                f[find(x+n)] = find(y+n);
                f[find(x+2*n)] = find(y+2*n);
            }
        } else {
            int fx = find(x);
            int fy = find(y);
            if (fx == fy|| find(x+2*n) == fy) {ans++;}
            else {
              f[find(x + n)] = fy;
              f[find(y+n)] = f[find(x+2*n)];
              f[find(y+2*n)] = fx;
            }
        }
    }
    printf("%d\n",ans);
}

Slip away, it's too delicious. The c + + experiment hasn't been written yet, and cf hasn't been scored yet (div3 can't ak all be spicy chicken, it's too delicious)