Before we know about LRU, we should know about cache. We all know that the computer has cache memory and can temporarily store the most commonly used data. When the cache data exceeds a certain size, the system will recycle it to free up space to cache new data, but the cost of retrieving data from the system is relatively high.

Cache requirements:

• Fixed size: the cache needs to have some restrictions to limit memory usage.
• Fast access: cache insert and lookup operations should be fast, preferably O(1) time.
• Replace entries when the memory limit is reached: the cache should have an effective algorithm to evict entries when the memory is full

If a cache replacement algorithm is provided to assist management, delete the least used data according to the set memory size, and actively release space before system recycling, the whole retrieval process will become very fast. Therefore, LRU cache elimination algorithm appears.

Principle and implementation of LRU

LRU (Least Recently Used) cache elimination algorithm It is proposed that the recently frequently accessed data should have higher retention, eliminate those infrequently accessed data, that is, the recently used data is likely to be used again, and discard the data that has not been accessed for the longest time, in order to facilitate the acquisition of data faster in the future. For example, Vue's keep live component is an implementation of LRU.

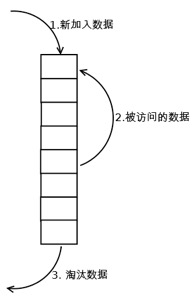
The central idea of implementation is divided into the following steps:

• Insert the new data into the head of the linked list.
• Whenever the cache hits (that is, the cached data is accessed), the data is moved to the head of the linked list.
• When the cache memory is full (when the number of linked lists is full), the data at the end of the linked list will be eliminated.

Example

Here is an example to illustrate the process of LRU implementation. Please refer to Refer here.

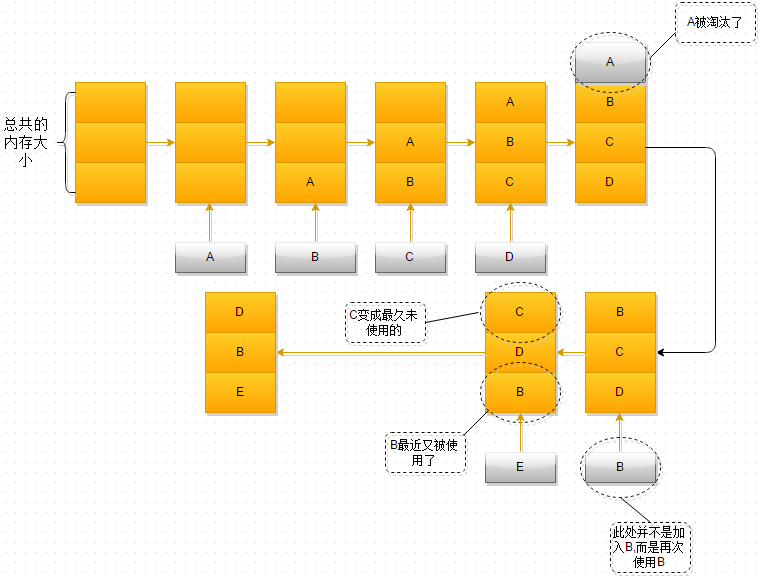
1. At first, the memory space is empty, so there is no problem entering A, B and C in turn
2. When D is added, there is A problem. The memory space is insufficient. Therefore, according to the LRU algorithm, A stays the longest in the memory space. Select A and eliminate it
3. When B is referenced again, B in the memory space is active again, while C becomes the most unused in the memory space in recent time
4. When E is added to the memory space again, the memory space is insufficient again. Select C that has stayed in the memory space for the longest time to eliminate it from the memory. At this time, the object stored in the memory space is E - > b - > D

Implementation of LRU based on bidirectional linked list and HashMap

The common LRU algorithm is based on bidirectional linked list and HashMap.

Bidirectional linked list: used to manage the order of cached data nodes. New data and cache hit (recently accessed) data are placed in the Header node, and the tail node is eliminated according to the memory size.

HashMap: stores the data of all nodes. When the LRU cache hits (data access), it intercepts and replaces and deletes the data.

Bidirectional linked list

Bidirectional linked list Is one of many linked lists, which are used Linked Storage Structure , every element in the linked list is called a data node.

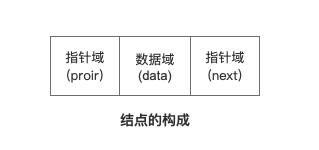
Each data node contains a data field and a pointer field. The pointer field can determine the order between nodes. The order of the linked list can be updated by updating the pointer field of the data node.

Each data node of the bidirectional linked list contains a data field and two pointer fields:

• proir points to the previous data node;
• Data the data of the current data node;
• Next points to the next data node;

The pointer field determines the order of the linked list, so the two-way linked list has a two-way pointer field, and the data nodes are not single pointing, but two-way pointing. That is, the proir pointer field points to the previous data node and the next pointer field points to the next data node.

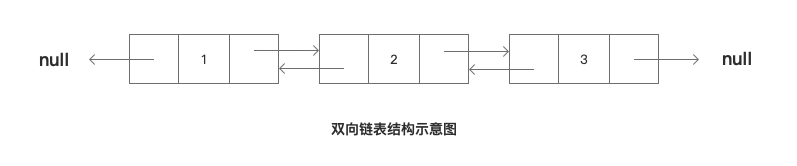
Similarly:

• One way linked list has only one pointer field.
• The circular (ring) linked list has a two-way pointer field, and the pointer field of the head node points to the tail node, and the pointer field of the tail node points to the head node.

Special nodes: Header and tail nodes

There are two special nodes in the linked list. Even the Header node and the tail node represent the head node and the tail node respectively. The head node represents the latest data or cache hit (recently accessed data), and the tail node represents the data node that has not been used for a long time and is about to be eliminated.

As an algorithm, everyone will pay attention to its time and space complexity O(n). Based on the advantages of the two-way pointer domain of the two-way linked list, in order to degrade the time complexity, in order to ensure that the new LRU data and the data hit by the cache are at the front of the linked list (Header), delete the last node (tail) when the cache is eliminated, and avoid traversal from beginning to end during data search, Reduce the time complexity of the algorithm. At the same time, based on the advantages brought by the two-way linked list, the pointer field of individual data nodes can be changed to update the linked list data. If the Header and tail nodes are provided as identification, the Header insertion method can be used to quickly increase the nodes. According to the tail node, the order of the linked list can also be quickly updated when the cache is eliminated, Avoid traversal from beginning to end and reduce the time complexity of the algorithm.

Sorting example

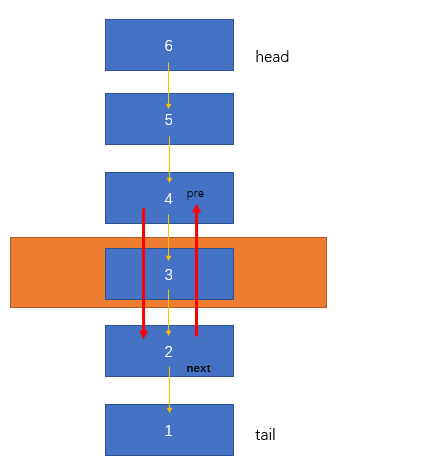
There are [6, 5, 4, 3, 2, 1] 6 data nodes in the LRU linked list, of which 6 is the Header node and 1 is the tail node. If data 3 is accessed (cache hit) at this time, 3 should be updated to the chain Header. The thinking of array should be to delete 3. However, if we take advantage of the two-way pointer of the two-way linked list, we can quickly update the linked list:

• When 3 is deleted, there are no other nodes between 4 and 2, that is, the next pointer field of 4 points to the data node where 2 is located; Similarly, the proir pointer field of 2 points to the data node where 2 is located.

HashMap

As for why HashMap is used, it can be summarized in one sentence, mainly because HashMap can be obtained much faster through Key, reducing the time complexity of the algorithm.

For example:

• When we get the cache from HashMap, the time complexity is basically controlled at O(1). If we traverse the linked list once, the time complexity is O(n).
• When accessing an existing node, we need to move the node to the header node. At this time, we need to delete the node in the linked list and add a new node after the header. At this time, go to the HashMap to get this node first, delete the node relationship, avoid traversing from the linked list, and reduce the time complexity from O(N) to O(1)

Since there is no relevant API for HashMap in the front end, we can use Object or Map instead.

code implementation

Now let's use the data structure we have to design and implement one, or reference LeeCode 146 questions.

Linked list node Entry

export class Entry<T> {

	value: T

	key: string | number

	next: Entry<T>

	prev: Entry<T>

	constructor(val: T) {
		this.value = val;
	}
}

Double Linked List

Main responsibilities:

• Manage head and tail nodes
• When inserting new data, move the new data to the header node
• Update delete node when deleting data The pointing domain of the front and rear nodes

/**
* Simple double linked list. Compared with array, it has O(1) remove operation.
* @constructor
*/
export class LinkedList<T> {

	head: Entry<T>
	tail: Entry<T>

	private _len = 0

	/**
	* Insert a new value at the tail
	*/
	insert(val: T): Entry<T> {
		const entry = new Entry(val);
		this.insertEntry(entry);
		return entry;
	}

	/**
	* Insert an entry at the tail
	*/
	insertEntry(entry: Entry<T>) {
		if (!this.head) {
			this.head = this.tail = entry;
		}
		else {
			this.tail.next = entry;
			entry.prev = this.tail;
			entry.next = null;
			this.tail = entry;
		}
		this._len++;
	}

	/**
	* Remove entry.
	*/
	remove(entry: Entry<T>) {
		const prev = entry.prev;
		const next = entry.next;

		if (prev) {
			prev.next = next;
		}
		else {
			// Is head
			this.head = next;
		}
		if (next) {
			next.prev = prev;
		}
		else {
			// Is tail
			this.tail = prev;
		}
		entry.next = entry.prev = null;
		this._len--;
	}

	/**
	* Get length
	*/
	len(): number {
		return this._len;
	}

	/**
	* Clear list
	*/
	clear() {
		this.head = this.tail = null;
		this._len = 0;
	}
}

LRU core algorithm

Main responsibilities:

• Add data to the linked list and update the linked list order
• The order in which the linked list is updated when the cache hits
• Memory overflow discards obsolete linked list data

/**

* LRU Cache

*/

export default class LRU<T> {

	private _list = new LinkedList<T>()

	private _maxSize = 10

	private _lastRemovedEntry: Entry<T>

	private _map: Dictionary<Entry<T>> = {}

	constructor(maxSize: number) {

		this._maxSize = maxSize;

	}

	/**

	* @return Removed value

	*/

	put(key: string | number, value: T): T {

		const list = this._list;

		const map = this._map;

		let removed = null;

		if (map[key] == null) {

			const len = list.len();

			// Reuse last removed entry

			let entry = this._lastRemovedEntry;

			if (len >= this._maxSize && len > 0) {

				// Remove the least recently used

				const leastUsedEntry = list.head;

				list.remove(leastUsedEntry);

				delete map[leastUsedEntry.key];

				removed = leastUsedEntry.value;

				this._lastRemovedEntry = leastUsedEntry;
				}
			if (entry) {
				entry.value = value;
			}
			else {
				entry = new Entry(value);
			}

			entry.key = key;
			list.insertEntry(entry);
			map[key] = entry;
		}
		return removed;
	}

	get(key: string | number): T {

		const entry = this._map[key];
		const list = this._list;

		if (entry != null) {
			// Put the latest used entry in the tail
			if (entry !== list.tail) {
				list.remove(entry);
				list.insertEntry(entry);
			}
			return entry.value;
		}
	}

	/**
	* Clear the cache
	*/
	clear() {
		this._list.clear();
		this._map = {};
	}

	len() {
		return this._list.len();
	}
}

Other LRU algorithms

In addition to the above common LRU algorithms, with the complexity and diversity of requirements, many optimization algorithms have been derived based on the idea of LRU, such as:

• LRU-K algorithm
• LRU two queues (2q) algorithm
• LRU multi queues (MQ) algorithm
• LFU algorithm
• LRU variant algorithm

Reference link

• Zrender - LRU
• Zhihu save elimination algorithm -- LRU algorithm
• LRU algorithm
• Detailed explanation and implementation of LRU strategy