Complexity of algorithm
Learn how to analyze the complexity of an algorithm.
Why algorithm complexity
Why do we need to introduce a concept of time complexity? Suppose we allow us to give the complexity of a code segment through running time directly on the server. This method becomes post statistics. What are the drawbacks of this approach?
- The factors affected by the physical machine are large. If the resource utilization on the machine is low at a certain time, it will lead to problems in your statistics
- It is greatly affected by the data. Such as sorting algorithm, different data order will affect the sorting algorithm.
Therefore, it is necessary to introduce a formula to express the relationship between the amount of data and the algorithm.
Representation of complexity
Large O complexity representation is commonly used. Represents the execution efficiency of the algorithm.
T(n) = O(f(n))
- T(n): indicates the execution time of the code.
- n: Represents the size of the data execution.
- f(n): represents the sum of the execution times of each line of code.
Time complexity
rule
Represents the direct relationship between code execution time and data size. Common rules:
Focus only on the code with the most cycles
The complexity representation method of large O only represents a change trend. We usually ignore the constants, low order and coefficients in the formula. We only need to record the magnitude of a maximum order.
for($i=0;$i<1000;$i++) { // do something } for($j=0;$i<2*$n;$j++) { // do something } // Time complexity: O(n)
Addition rule: the total complexity is equal to the complexity of the code with the largest order of magnitude
for($i=0;$i<$n;$i++) { // do something } for($j=0;i<$n*$n;$j++) { // do something } // Time complexity: O(n^2)
Multiplication rule: the complexity of nested code is equal to the product of the complexity of inner and outer nested code
for($i=0;$i<$n;$i++) { for($j=0;$i<$n;$j++) { // todo } } // Time complexity: O(n^2)
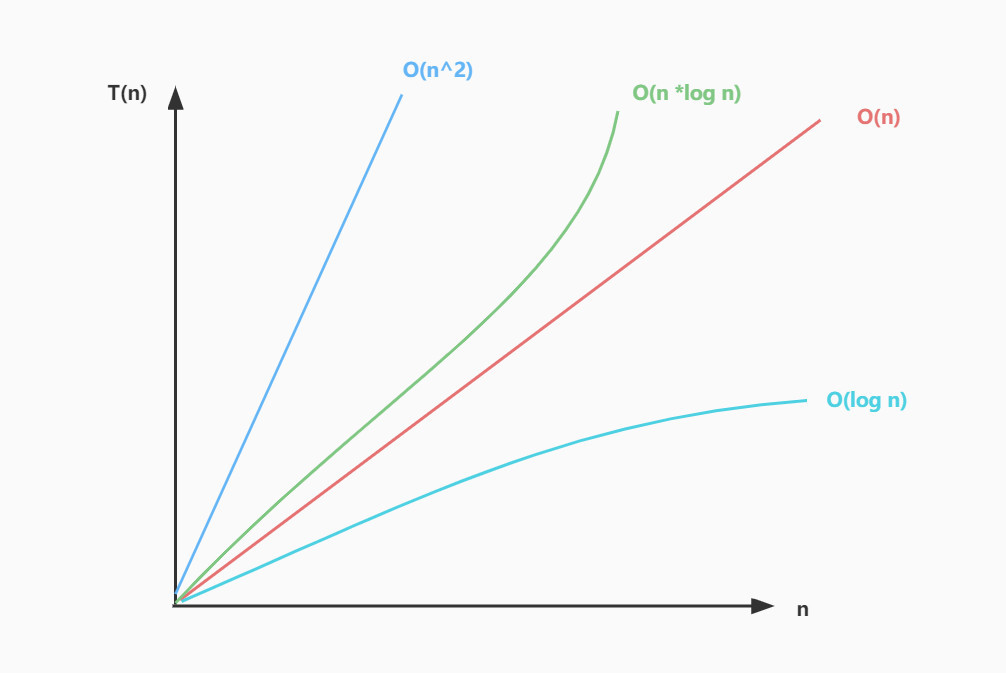
Common time complexity
Increase abnormally by order of magnitude
| Complexity formula | describe |
|---|---|
| O(1) | Constant order |
| O(log n) | Logarithmic order |
| O(n) | Linear order |
| O(n *log n ) | Linear logarithmic order |
| O(n^2), O(n^K) | K-th order |
| O(2^n) | Exponential order O |
| O(n!) | Factorial |
O(1):
Indicates the constant level, that is, the execution time of the code has nothing to do with the amount of data.
$a = 3; $b = 4; $sum = $a + $b;
O(log n):
In the following code, $I is an equal ratio sequence from 1,2,4,8,16... And the number of executions is equal to the logarithm of N with 2 as the base, i.e. O (log n).
Whether the following code is multiplied by 2 or 3, the time complexity remains the same. Because logarithms can be transformed. log3n is equal to log32 * log2n. So we ignore the base
$i = 1; while(i<n) { $i = $i *2; }
O(nlog n)
The famous quick sort and merge sort are all of this complexity.
O(m+n), O(m*n)
Complexity is determined by two parameters, and we cannot predict the size of these two parameters
function sumAdd($m, $n) { for($i=0;$i<$m;$i++) { $m += $i } for($j=0;$j<$n;$j++) { $n += $i } return $m+$n }
classification
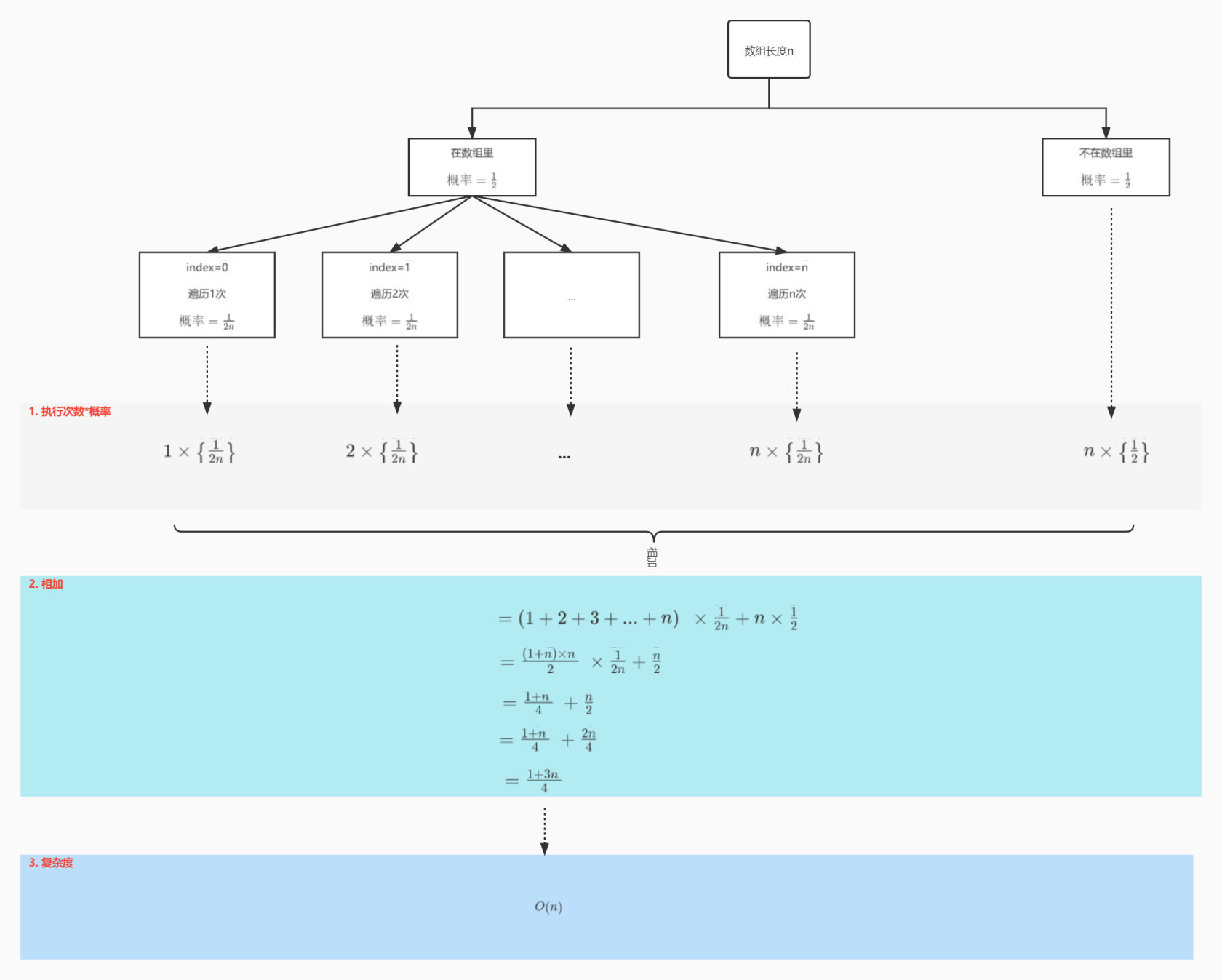
It is classified as: best time complexity, worst time complexity, average time complexity and average time complexity. What is the time complexity for the following code?
function FindIndex(array $array, $value)
{
$index = -1;
for($i=0;$i<len($array);$i++) {
if ($array[$i] == $value) {
$index = $i;
break;
}
}
return $index;
}Best time complexity
Ideally, the time complexity of executing this code. As shown in the above code, the best time complexity is O(1).Worst time complexity
In the worst case, the time complexity of executing this code. Then the above worst time complexity O(n).
Average time complexity (weighted average time complexity or expected time complexity)
That is, the result of multiplying the probability by the running time. The following figure shows the average complexity derivation formula of the above code
Sharing time complexity
Spread the behavior with higher time complexity to lower time complexity.
There are few application scenarios with this complexity. That is, operations with different complexity occur regularly. We can spread operations with high complexity to lower time complexity. Generally, the average sharing time complexity is equal to
// Traverse the array, insert the value and random number, and calculate the length of the array the last time function InsertAndSum(array $array, $value) { $sum = 0; $n = len($array); for($i=0;$i<$n ;$i++) { $array[$i] = $value + mt_rand(10,100); if ($i == $n-1) { // last hole for($j=0;$j<$n ;$j++) { $sum += $array[$j]; } } } return $sum; } // 1. In N cycles, the time complexity of N-1 cycles is O (1), and that of 1 cycle is O(n) // 2. Average the time complexity of the last time to the previous N-1 times // 3. The average sharing time complexity is O(1)
Spatial complexity
Progressive space complexity, which represents a relationship function between data and storage space.
function NewArray($n)
{
$a = 'cx';
$b = new SplFixedArray($n);
for($i=0;$i<$n;$i++) {
$b[$i] = $a;
}
}
// The space complexity of this code is O(n), because an N memory space is requested in line 4Common spatial complexity
O(1)
function NewArray($n) { $a = 'cx'; return $a; }
O(n)
function NewArray($n) { $a = 'cx'; $b = new SplFixedArray($n); for($i=0;$i<$n;$i++) { $b[$i] = $a; } }
O(n^2)
function NewArray($n) { $a = 'cx'; $b = new SplFixedArray($n*$n); for($i=0;$i<$n*$n;$i++) { $b[$i] = $a; } }
Complexity trend