1: Hanoi Tower problem

Interview question 08.06. Hanoi Tower question LeetCode (LeetCode CN. Com)https://leetcode-cn.com/problems/hanota-lcci/

class Solution {
public:
void zhuanYi(int i,vector<int>&from,vector<int>&other,vector<int>&to){
    if(i==1){int ding=from.back();from.pop_back();to.push_back(ding);}
    else{
        zhuanYi(i-1,from,to,other);//from to other
        int ding=from.back();
        from.pop_back();
        to.push_back(ding);
        cout<<"i-1 yes"<<i-1<<endl;
        cout<<other.size()<<endl;
        zhuanYi(i-1,other,from,to);
    }
}
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        zhuanYi(A.size(),A,B,C);
    }
};

2: Full Permutation (use "branch and bound" to kill the repeated path in advance to realize no repetition) (do not open up a new array, but directly change the position of the original array)

Loading Question... - LeetCode (LeetCode CN. Com)https://leetcode-cn.com/problems/permutations-ii/submissions/

class Solution {
public:
        void xunhuan(vector<int>&nums,int i,vector<vector<int>>&result){
            if(i==nums.size()){
                result.push_back(nums);return;
            }
            unordered_set<int>xi;
            for(int j=i;j<nums.size();j++){
                if(xi.count(nums[j])!=0){continue;}
                xi.insert(nums[j]);
                //Three hash functions: insert, erase, count,
                //find: judge whether there is map.find(key) == map.end(),
                swap(nums[i],nums[j]);
                xunhuan(nums,i+1,result);
                swap(nums[i],nums[j]);
            }
        }

    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>>result;
        xunhuan(nums,0,result);
        return result;
    }
};

Taking the simplest three elements as an example, the full arrangement of elements can be roughly described as fixing the first few bits and then exchanging the last two bits.

The idea of full arrangement of multiple elements is probably the same,

Exchange the elements after bit i with the current i element, that is, i and its subsequent elements can take turns to do the position of i. For each sub case of the position of i, the next element is appointed in the same way. Until the tail is processed, a result is processed and recursive step by step.

At the same time, in order not to produce duplicate results (the so-called duplicate results are mainly because there are the same elements in the array, which will cause the same elements to have made a bit)

When traversing the sub case of the ith bit, set up a hash set to store who has done it in the ith position to prevent repetition.

Compared with the method of removing the repetition of all results, there is no optimization in the index (no optimization in the worst case), but there is optimization in the constant term.

Another: the three hash functions: insert, erase, count,
find: judge whether there is map.find(key) == map.end(),

3: Given an integer array arr, cards with different values are arranged in A line. Player A and player B take each card in turn. It is stipulated that player A takes it first and player B takes it later. But each player can only take the leftmost or rightmost cards at A time. Player A and player B are extremely smart. Please return the score of the final winner.

#include <bits/stdc++.h>

using namespace std;


int s(vector<int>arr, int i, int j);//When the sub functions call each other, you can prove it first and then write a specific

int f(vector<int>arr, int i, int j) { //Return to the first hand
	if (i == j) {
		return arr[i];
	}

	return max( arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
}

int s(vector<int>arr, int i, int j) {
	if (i == j) {
		return 0;
	}

	return min( f(arr, i + 1, j), f(arr, i, j - 1) );
}

int win(vector<int>arr) {
	if (arr.size() == 0) {
		return 0;
	}

	return max( f(arr, 0, arr.size() - 1), s(arr, 0, arr.size() - 1 ));
}

int main() {
	vector<int>arr;
	int pp;

	while (cin >> pp) {
		arr.push_back(pp);
	}

	//At the end of input, enter a character (because the character does not match the attribute of the vector) to end input, or press ctrl+z to end input
	//Or add a termination identifier

	return win(arr);
}

4: Reverse order of stack (no new data structure)

#include <iostream>
#include <stack>
using namespace std;

int f(stack<int> &p) { //Return to the bottom element and press down
	int ding = p.top();
	p.pop();

	if (p.empty()) {
		return ding;
	} else {
		int last = f(p);
		p.push(ding);
		return last;
	}
}

void reverse(stack<int> &p) {
	if (p.empty()) {
		return;
	}

	int i = f(p); //Get the bottom and press down
	reverse(p);
	p.push(i);
}

int main() {
	stack<int>p;
	for (int i = 0; i < 10; i++) {
		p.push(i + 1);
	}
//
//	Cout < < output from the top of the stack to the bottom of the stack < < endl;
//	stack<int>q;
//	q = p;
//
//	while (!q.empty()) {
//		cout << q.top() << endl;
//		q.pop();
//	}

	reverse(p);
//	Cout < < output from the top of the stack to the bottom of the stack < < endl;
//
//	while (!p.empty()) {
//		cout << p.top() << endl;
//		p.pop();
//	}

	return 0;
}

5: If 1 corresponds to A, 2 corresponds to B, 3 corresponds to C... 26 corresponds to Z, then A numeric string such as "111" can be converted into: "AAA", "KA" and "AK". Given A string str composed of only numeric characters, how many conversion results are there?

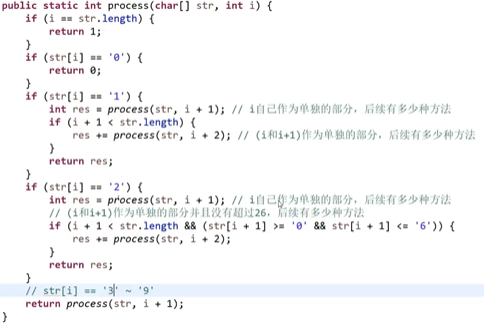
  6: Given two arrays of length N, weights and values, weights[i] and values[i] represent   The weight and value of item I. given a positive bag, it means a bag with a load. You can't load more than this weight. Return the maximum value you can load?