Steps:
1) Find out what variable parameters can represent a recursive state, that is, once the parameters are determined, the return value is determined
2) All combinations of variable parameters are mapped into a table. One variable parameter is a one-dimensional table, and two variable parameters are
Is a two-dimensional table
3) The final answer is which position in the table and mark it in the table
4) According to the base case of the recursive process, fill in the simplest positions in the table that do not need to depend on other positions
value
5) According to the non base case part of the recursive process, that is, how to calculate the general position in the analysis table, that is
Then the filling order of this form will be determined
6) Fill out the form and return the value of the final answer in the table
2. Look at the questions:
The number of methods for the robot to reach the specified position assumes that there are n positions arranged in a row, which are recorded as 1~N, and N must be greater than or equal to 2. At the beginning, when the robot is in position m (M must be one of 1~N), the robot can go left or right. If the robot comes to position 1, the next step can only go right to position 2; If the robot comes to position n, the next step can only go to position N-1 to the left. How many methods stipulate that the robot must take K steps and finally reach position P (P must also be one of 1~N). Given four parameters N, m, K and P, return the number of methods.
Method 1: recursion
public class solution {
public static int ways1(int N, int M, int K, int P) {
// Invalid parameter, return 0 directly
if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
return 0;
}
// There are N positions in total. Starting from point M, there are K steps left, and the number of methods that can finally reach P is returned
return walk(N, M, K, P);
}
// N: position is 1 ~ N, fixed parameter
// Cur: currently in cur position, variable parameter
// rest: there are still res steps left, variable parameters
// P: the final target position is p, with fixed parameters
// Meaning of this function: it can only move in 1~N positions. It is currently in cur position. After taking the rest step, the number of methods stopped at P position is returned as the return value
public static int walk(int N , int cur , int rest, int P){
// If there are no more steps left, the current cur position is the last position
// If the last position stops on P, the previous movement is effective
// If the last position is not on P, the previous movement is invalid
if(rest==0){
return cur==P?1:0;
}
// If there are still rest steps to go, and the current cur position is at position 1, then the current step can only move from 1 to 2
// The follow-up process is to come to position 2, and there are still rest-1 steps to go
if(cur==1){
return walk(N,2,res-1,P);
}
// If there is still a rest step to go, and the current cur position is in position N, then the current step can only move from N to N-1
// The follow-up process is to come to the N-1 position, and there are still rest-1 steps to go
if(cur==N){
return walk(N,N-1,res-1,P);
}
// If there are still rest steps to go, and the current cur position is in the middle position, the current step can go left or right
// After moving to the left, the subsequent process is to come to the cur-1 position, and there are still rest-1 steps to go
// After going to the right, the subsequent process is to come to cur+1, and there are still rest-1 steps to go
// Moving to the left and to the right are different methods, so the total number of methods should be counted
return walk(N,cur+1,res-1,P)+walk(N,cur-1,res-1,P);
}
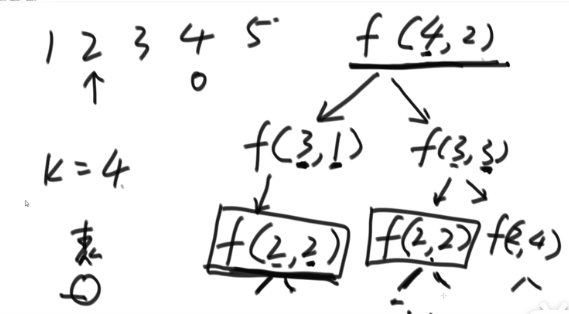
}Optimization 1: there are many repeated calculations in the recursive process. Add a two-dimensional table as a cache.
f(2,2,) repeated calculation
public class solution {
public static int ways2(int N, int M, int K, int P) {
int[][] dp =new int [K+1][N+1];
for(int i=0;i<=K;i++){
for(int j=0;j<=N;j++){
dp[i][j]=-1;
}
}
// Invalid parameter, return 0 directly
if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
return 0;
}
// There are N positions in total. Starting from point M, there are K steps left, and the number of methods that can finally reach P is returned
return walk(N, M, K, P,dp);
}
public static int walk(int N , int cur , int rest, int P,int[][] dp){
if(dp[rest][cur]!=-1){ //First judge whether the calculated position exists in the two-dimensional table
return dp[rest][cur];
}
if(rest==0){
dp[rest][cur]=cur==P?1:0;
}
if(cur==1){
dp[rest][cur]=walk(N,2,res-1,P);
}
else if(cur==N){
dp[rest][cur]=walk(N,N-1,res-1,P)
}
else{
dp[rest][cur]=walk(N,cur+1,res-1,P)+walk(N,cur-1,res-1,P)
}
return dp[rest][cur];
}
}Optimization 3: turn to dynamic programming.
In fact, it is a process of creating tables.
Initial assignment: cur has no 0 position, so there is no number in column 0. Can be initially - 1.
When rest is 0, only cur is 1 at the end position.
The calculation of the remaining points is equal to

public static int way3(int N, int M, int K, int P) {
int[][] dp =new int [K+1][N+1];
for(int i=1;i<=K;i++){
for(int j=1;j<=N;j++){
if(j==1){ //Special boundary treatment
dp[i][j]=dp[i-1][2];
}else if(j==N){
dp[i][j]=dp[i-1][N-1];
}else{
dp[i][j]=dp[i-1][cur+1]+dp[i-1][cur-1];//Related to the upper left and upper right values
}
}
}
return dp[K][M];
}Topic 2: the minimum amount of money to change
class solution{
public static int minCoins(int[] arr,int aim){
if(arr=null || aim<0 || arr.length==0){
return -1;
}
return process(arr,0,aim); //Each index has two choices: take it or not
}
// At present, the par value considered is arr[i], and the rest money needs change
// If - 1 is returned, it means that if the par value of arr[i..N-1] is used freely, the change rest cannot be made anyway
// If the return is not - 1, it represents the minimum number of sheets required for change rest in the case of free use of arr[i..N-1] face value
public static int process(int[] arr, int index, int rest){
// There is no face value to consider
// If the remaining money is 0, 0 will be returned
// If the remaining money is not 0, return - 1
if(res<0){
return -1;
}
if(rest=0)
{
return 0;
}
if(i==arr.length){
return rest==-1;
}
int p1=process(arr,index+1,rest);//Not take
int p2=process(arr,index+1,res-arr[index]);//take
if(p1==-1 && p2==-1){
return -1;
}else{
if(p1==-1){
return p1=p2+1;
}
if(p2==-1){
return p1;
}
return Math.min(p1,p2+1);
}
}
}dynamic programming

public static int minCoins(int[] arr , int aim){
int N =arr.length;
int [][] dp= new int[N+1][aim+1];
//Initial table assignment
for(itn row=0;row<=N;row++){
dp[row][0]=0;
}
for(int col=1;col<=aim;col++){
dp[N][col]=-1;
}
for(int index=N-1;index>=0;index--){
for(int rest=1;rest<=aim;rest++){
int p1=dp[index+1][rest];
int p2=-1;
if(rest-arr[index]>=0){
p2=dp[index+1][rest-arr[index]];
}
if(p1==-1 && p2==-1){
dp[index][rest]=-1;
}else{
if(p1==-1){
dp[index][rest]=p2+1;
}
else if(p2==-1){
dp[index][rest]=p1;
}else{
dp[index][rest]=Math.min(p1.p2+1);
}
}
}
return dp[0][aim];
}