The Title roughly means that in a given rectangle, given n circles (0).n1000) is an obstacle that allows you to find a path from x=0 to x=1000. I was wrong at first, and then I saw the explanation of the big man. Then I realized that we could make DFS from top to bottom by circle. It means that we should first find the circle tangent or intersect with y=1000, then do DFS to search for the circle that intersects or intersects with it. If the circle and x=0 are tangent or intersect, we can use y-r-x* x to find the top point (drawing a picture is easier to understand).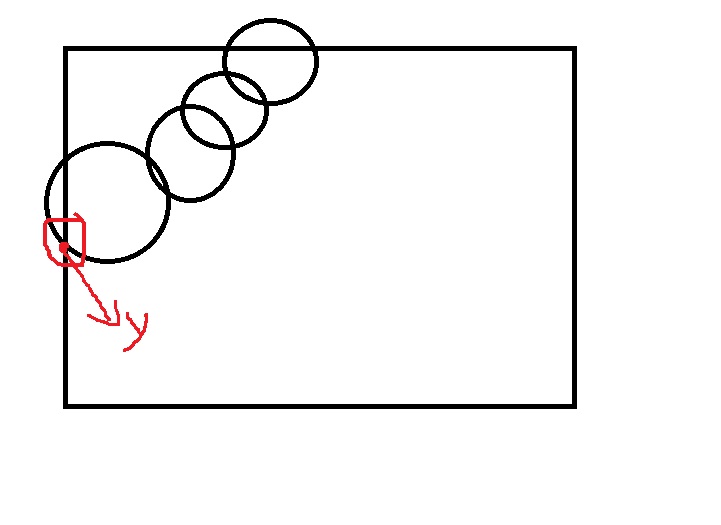

The same is true for x=1000. It should be noted that all points intersecting or tangential with y=1000 must be traversed, because if the lowest y=0 has not been reached before, it does not mean that the next circle cannot traverse y=0. The points traversed need not be traversed again.

#include<iostream>
#include <string.h>
#include <algorithm>
#include<math.h>
using namespace std;
int n;
struct Node
{
	double x, y, r;
};
double wid = 1000.00;
Node Enemy[1010];
int vis[1010]; double start = 1000.00, endans = 1000.00;
bool dfs(int u)
{
	vis[u] = 1;
	if (Enemy[u].y - Enemy[u].r <= 0.0)return true;
	if(Enemy[u].x<=Enemy[u].r)
	{
		start = min(Enemy[u].y-sqrt(Enemy[u].r*Enemy[u].r - Enemy[u].x*Enemy[u].x), start);
	}
	if(Enemy[u].x+Enemy[u].r>=wid)
	{
		endans = min(Enemy[u].y-sqrt(Enemy[u].r*Enemy[u].r - (wid-Enemy[u].x)*(wid-Enemy[u].x)), endans);
	}
	for(int i=0;i<n;i++)
	{
		if(!vis[i]&&(sqrt((Enemy[i].x-Enemy[u].x)*(Enemy[i].x-Enemy[u].x)+ (Enemy[i].y - Enemy[u].y)*(Enemy[i].y - Enemy[u].y))<=(Enemy[i].r+Enemy[u].r)))
		{
			if(dfs(i))return true;
		}
	}
	return false;
}
int main()
{
    while(cin >> n)
    {
		memset(vis, 0, sizeof(vis));
		memset(Enemy, 0, sizeof(Enemy));
	    for(int i=0;i<n;i++)
	    {
			cin >> Enemy[i].x >> Enemy[i].y >> Enemy[i].r;
	    }
			bool isflag = false;
		for(int i=0;i<n;i++)
		{
			if(Enemy[i].y+Enemy[i].r>=wid)
			{
				if(!vis[i]&&dfs(i))
				{
					cout << "IMPOSSIBLE" << endl;
					isflag = true;
					break;
				}
			}
		}
		if(!isflag)		printf("0.00 %.2lf 1000.00 %.2lf\n", start, endans);
				start = 1000.00; endans = 1000.00; 
    }
	
	return 0;
}