Ensemble learning

Using a single model can not achieve the best results, so we consider using ensemble learning method to further reduce the error.
Integrated learning is the stacking and integration of different models and the selection of optimal parameters.
Thirteen models will be used in ensemble learning. First, import the packages that need to be used.

from sklearn.model_selection import cross_val_score, GridSearchCV, KFold
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, ExtraTreesRegressor
from sklearn.svm import SVR, LinearSVR
from sklearn.linear_model import ElasticNet, SGDRegressor, BayesianRidge
from sklearn.kernel_ridge import KernelRidge
from xgboost import XGBRegressor

1. Basic Modeling and Evaluation

According to the requirements of the competition, the cross validation evaluation index based on RMSE is defined at first.

#Define cross-validation strategies and evaluation functions
def rmse_cv(model,X,y):
    rmse = np.sqrt(-cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=5))
    return rmse

Save all the models to be used

models = [LinearRegression(),Ridge(),Lasso(alpha=0.01,max_iter=10000),RandomForestRegressor(),GradientBoostingRegressor(),SVR(),LinearSVR(),
          ElasticNet(alpha=0.001,max_iter=10000),SGDRegressor(max_iter=1000,tol=1e-3),BayesianRidge(),KernelRidge(alpha=0.6, kernel='polynomial', degree=2, coef0=2.5),
          ExtraTreesRegressor(),XGBRegressor()]

Firstly, 13 models and 5-fold cross-validation are used to evaluate the prediction effect of each model.

names = ["LR", "Ridge", "Lasso", "RF", "GBR", "SVR", "LinSVR", "Ela","SGD","Bay","Ker","Extra","Xgb"]
for name, model in zip(names, models):
    score = rmse_cv(model, X_scaled, y_log)
    print("{}: {:.6f}, {:.4f}".format(name,score.mean(),score.std()))

LR: 621771864740.772827, 411989810656.7503
Ridge: 0.118922, 0.0076
Lasso: 0.118914, 0.0065
RF: 0.148033, 0.0049
GBR: 0.123131, 0.0076
SVR: 0.179019, 0.0129
LinSVR: 1.239646, 0.4882
Ela: 0.116366, 0.0070
SGD: 2.814280, 0.5916
Bay: 0.117589, 0.0066
Ker: 0.114100, 0.0081
Extra: 0.141861, 0.0112
Xgb: 0.124880, 0.0058

2. Adjusting the parameters of each model

Establish a parameter adjustment method, where the evaluation index is RMSE, so the printed score should also be RMSE. Define the crossover mode, specify the model first and then specify the parameters, which is convenient to test multiple models, and use grid cross validation.

class grid():
    def __init__(self,model):
        self.model = model
    
    def grid_get(self,X,y,param_grid):
        grid_search = GridSearchCV(self.model,param_grid,cv=5, scoring="neg_mean_squared_error")
        grid_search.fit(X,y)
        print(grid_search.best_params_, np.sqrt(-grid_search.best_score_))
        grid_search.cv_results_['mean_test_score'] = np.sqrt(-grid_search.cv_results_['mean_test_score'])
        print(pd.DataFrame(grid_search.cv_results_)[['params','mean_test_score','std_test_score']])

Result of Lasso()

grid(Lasso()).grid_get(X_scaled,y_log,{'alpha': [0.0004,0.0005,0.0007,0.0006,0.0009,0.0008],'max_iter':[10000]})

{'alpha': 0.0009, 'max_iter': 10000} 0.11557402177546283
                                 params  mean_test_score  std_test_score
0  {'alpha': 0.0004, 'max_iter': 10000}         0.116897        0.001659
1  {'alpha': 0.0005, 'max_iter': 10000}         0.116580        0.001644
2  {'alpha': 0.0007, 'max_iter': 10000}         0.116041        0.001612
3  {'alpha': 0.0006, 'max_iter': 10000}         0.116301        0.001630
4  {'alpha': 0.0009, 'max_iter': 10000}         0.115574        0.001574
5  {'alpha': 0.0008, 'max_iter': 10000}         0.115794        0.001591

Result of Ridge()

grid(Ridge()).grid_get(X_scaled,y_log,{'alpha':[35,40,45,50,55,60,65,70,80,90]})

{'alpha': 90} 0.11753822142197719
          params  mean_test_score  std_test_score
0  {'alpha': 35}         0.118097        0.001621
1  {'alpha': 40}         0.118003        0.001607
2  {'alpha': 45}         0.117921        0.001595
3  {'alpha': 50}         0.117849        0.001583
4  {'alpha': 55}         0.117787        0.001573
5  {'alpha': 60}         0.117733        0.001564
6  {'alpha': 65}         0.117686        0.001555
7  {'alpha': 70}         0.117646        0.001547
8  {'alpha': 80}         0.117582        0.001533
9  {'alpha': 90}         0.117538        0.001522

After many rounds of testing, the following six models and their corresponding optimal parameters are finally selected.

lasso = Lasso(alpha=0.0005,max_iter=10000)
ridge = Ridge(alpha=60)
svr = SVR(gamma= 0.0004,kernel='rbf',C=13,epsilon=0.009)
ker = KernelRidge(alpha=0.2 ,kernel='polynomial',degree=3 , coef0=0.8)
ela = ElasticNet(alpha=0.005,l1_ratio=0.08,max_iter=10000)
bay = BayesianRidge()

3. Integration method, using weighted averaging

Weighted average of each model according to weight

##Defining a weighted average is equivalent to writing fit_transform()
class AverageWeight(BaseEstimator, RegressorMixin):
    def __init__(self,mod,weight):
        self.mod = mod##Number of models
        self.weight = weight##weight
        
    def fit(self,X,y):
        self.models_ = [clone(x) for x in self.mod]
        for model in self.models_:
            model.fit(X,y)
        return self
    
    def predict(self,X):
        w = list()
        # pred returns the cross-validation results for each model in size (number of models) x (number of samples in validation set)
        pred = np.array([model.predict(X) for model in self.models_])
        # For each data point, a single model is multiplied by weights and then added up.
        for data in range(pred.shape[1]):
            single = [pred[model,data]*weight for model,weight in zip(range(pred.shape[0]),self.weight)]
            w.append(np.sum(single))
        return w

Define six initial weights

w1 = 0.02
w2 = 0.2
w3 = 0.25
w4 = 0.3
w5 = 0.03
w6 = 0.2

weight_avg = AverageWeight(mod = [lasso,ridge,svr,ker,ela,bay],weight=[w1,w2,w3,w4,w5,w6])
print(rmse_cv(weight_avg,X_scaled,y_log))  
print(rmse_cv(weight_avg,X_scaled,y_log).mean())##Calculate the mean of cross validation

[0.11579461, 0.12567714, 0.12194691, 0.10298115, 0.11307847]
0.11589565350500453

4. stacking model stacking

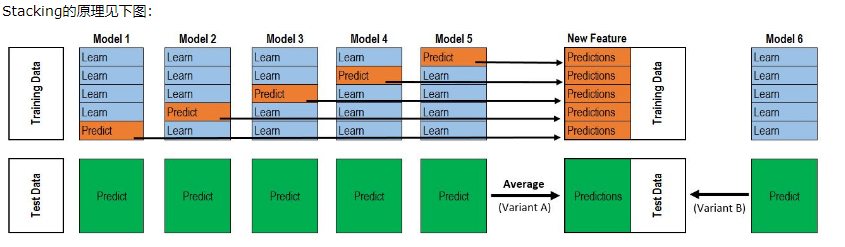
class stacking(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self,mod,meta_model):
        self.mod = mod
        self.meta_model = meta_model#Meta model
        self.kf = KFold(n_splits=5, random_state=42, shuffle=True)##That's the biggest feature of stacking. It's broken down a few times.
        
    def fit(self,X,y):
        self.saved_model = [list() for i in self.mod] # Preservation model
        oof_train = np.zeros((X.shape[0], len(self.mod))) # Here we get a matrix of the number of rows multiplied by the number of models in the training set.
        
        for i,model in enumerate(self.mod):#What is returned is the index and the model itself.
            for train_index, val_index in self.kf.split(X,y):##The data returned is from the province.
                renew_model = clone(model)##Model replication
                renew_model.fit(X[train_index], y[train_index])#Training data
                self.saved_model[i].append(renew_model)##Add the model in
                oof_train[val_index,i] = renew_model.predict(X[val_index])##Used to predict validation sets
        
        self.meta_model.fit(oof_train,y)#Meta model
        return self
    
    def predict(self,X):
        whole_test = np.column_stack([np.column_stack(model.predict(X) for model in single_model).mean(axis=1) 
                                      for single_model in self.saved_model]) ##What you get is the entire test suite.
        return self.meta_model.predict(whole_test)#What is returned is to use the metamodel to predict the entire test set.
    
    def get_oof(self,X,y,test_X):
        oof = np.zeros((X.shape[0],len(self.mod)))##Initialization is 0
        test_single = np.zeros((test_X.shape[0],5))##Initialization is 0 
        test_mean = np.zeros((test_X.shape[0],len(self.mod)))
        for i,model in enumerate(self.mod):##i is a model.
            for j, (train_index,val_index) in enumerate(self.kf.split(X,y)):##j is all partitioned data
                clone_model = clone(model)##Cloning module is equivalent to copying the model.
                clone_model.fit(X[train_index],y[train_index])##Training the segmented data
                oof[val_index,i] = clone_model.predict(X[val_index])##Predicting Verification Sets
                test_single[:,j] = clone_model.predict(test_X)##Predicting test sets
            test_mean[:,i] = test_single.mean(axis=1)##Test Setting Well Means
        return oof, test_mean

##After preprocessing, it can be placed in a stacked model for calculation.
a = Imputer().fit_transform(X_scaled)#Equivalent to x
b = Imputer().fit_transform(y_log.values.reshape(-1,1)).ravel()#Equivalent to y

stack_model = stacking(mod=[lasso,ridge,svr,ker,ela,bay],meta_model=ker)
stack_model.fit(a,b)#Model training
pred = np.exp(stack_model.predict(test_X_scaled))#Forecast
result.to_csv("submission2.csv",index=False)

The post-upload score was 0.12310