The main idea of the topic

Given a tree with N points, the weight of all nodes is 0. There are k operations, each time two points s,t are specified, the weights of all points on the path from s to t are added by one, and finally the weight of the point with the largest weight after K operations is output.

Analysis

It's a template problem of tree difference.

Say the ordinary difference. Now there is A problem. Given A sequence A, there are K modifications. Each modification adds 1 to the number in [L,R], and finally asks the maximum number. The most common method is to run [L,R] once A time and update the maximum value. Obviously, this may lead to TLE. The difference method will convert interval modification into point modification. Define the differential sequence D,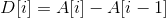The prefix sum of D is the original array. And if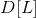At + 1, for all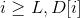Will be + 1 in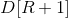- 1, for all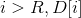Both - 1 and + 1 offset the overlap, so only [L,R] is changed. After the modification, count the prefix sum and find the maximum number.

The same is true for differences in trees. If you want the weight of each edge from u to v in the graph to be + 1, you can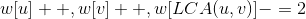Among them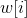Express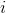The edge between node No. 1 and its father is counted by DFS once, i.e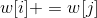(i is j's father).

For the difference of point weight, it's almost the same. Let's reduce it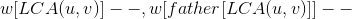Because for a point,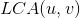In this chain, and it can only add one, so + +, it + +, its father will + +, so its father will --.

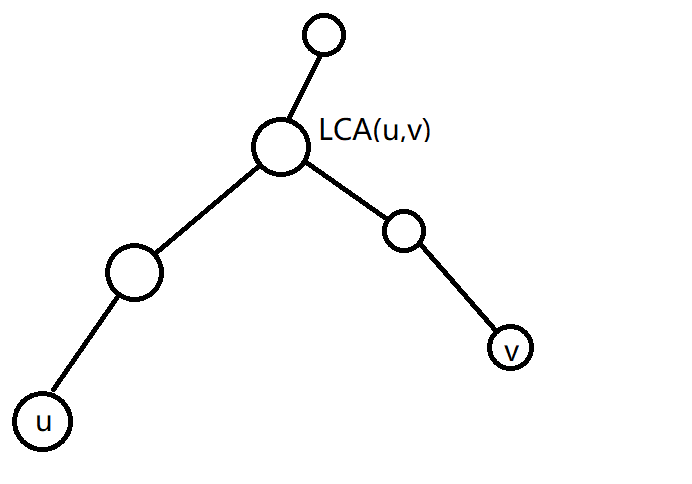
This question is the difference of point according to the meaning of the question, so follow the second method.

Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <map>
#include <queue>
using namespace std;
struct node {
	int to,next;
}e[50005*2];
int h[50005],cnt,dth;
int n,k,dep[50005],ans;
int f[50005][20],v[50005];
void add(int x,int y) {
	e[++cnt]=(node){y,h[x]};
	h[x]=cnt;
}
void FindDepth(int x,int prt) {
	dep[x]=dep[prt]+1;
	for (int i=h[x];i;i=e[i].next) {
		int y=e[i].to;
		if (y==prt) continue;
		f[y][0]=x;
		FindDepth(y,x);
	}
}
int GetLca(int x,int y) {
	if (dep[x]<dep[y]) swap(x,y);
	for (int i=dth;i>=0;i--)
		if (dep[f[x][i]]>=dep[y]) x=f[x][i];
	if (x==y) return x;
	for (int i=dth;i>=0;i--)
		if (f[x][i]!=f[y][i])
			x=f[x][i],y=f[y][i];
	return f[x][0];
}
void Dfs(int x,int prt) {
	for (int i=h[x];i;i=e[i].next) {
		int y=e[i].to;
		if (y==prt) continue;
		Dfs(y,x);
		v[x]+=v[y];
	}
	ans=max(ans,v[x]);
}
int main() {
	scanf("%d%d",&n,&k);
	for (int i=1,a,b;i<n;i++) {
		scanf("%d%d",&a,&b);
		add(a,b);
		add(b,a);
	}
	dth=(int)(log(n)/log(2));
	FindDepth(1,0);
	for (int j=1;(1<<j)<=n;j++)
		for (int i=1;i<=n;i++)
			f[i][j]=f[f[i][j-1]][j-1];
	
	for (int i=1,a,b;i<=k;i++) {
		scanf("%d%d",&a,&b);
		v[a]++;
		v[b]++;
		int t=GetLca(a,b);
		v[t]--;
		v[f[t][0]]--;
	}
	Dfs(1,0);
	printf("%d",ans);
	return 0;
}