Because there has been no time recently, so this blog has not been published. Now I will talk about uv drawing arc, circle, irregular surface stitching.
First two renderings
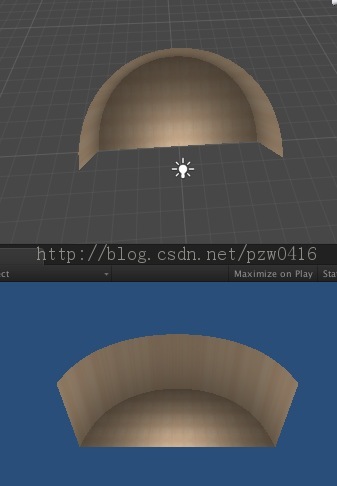
I think it's relatively simple. Of course, you can also use the equation of circle. The equation of parabola can achieve this effect.
But I prefer to use Bessel. If you know ps, you know there is a pen tool in it. It's Bessel's principle. Bessel's algorithm can be searched online.
There are also many Bessel computing methods on the Internet.
Let's start with my code
using UnityEngine;
[System.Serializable]
public class Bezier : System.Object
{
public Vector3 p0;
public Vector3 p1;
public Vector3 p2;
public Vector3 p3;
public float ti = 0f;
private Vector3 b0 = Vector3.zero;
private Vector3 b1 = Vector3.zero;
private Vector3 b2 = Vector3.zero;
private Vector3 b3 = Vector3.zero;
private float Ax;
private float Ay;
private float Az;
private float Bx;
private float By;
private float Bz;
private float Cx;
private float Cy;
private float Cz;
public Bezier( Vector3 v0, Vector3 v1, Vector3 v2, Vector3 v3 )
{
this.p0 = v0;
this.p1 = v1;
this.p2 = v2;
this.p3 = v3;
}
// 0.0 >= t <= 1.0
public Vector3 GetPointAtTime( float t )
{
this.CheckConstant();
float t2 = t * t;
float t3 = t * t * t;
float x = this.Ax * t3 + this.Bx * t2 + this.Cx * t + p0.x;
float y = this.Ay * t3 + this.By * t2 + this.Cy * t + p0.y;
float z = this.Az * t3 + this.Bz * t2 + this.Cz * t + p0.z;
return new Vector3( x, y, z );
}
private void SetConstant()
{
this.Cx = 3f * ( ( this.p0.x + this.p1.x ) - this.p0.x );
this.Bx = 3f * ( ( this.p3.x + this.p2.x ) - ( this.p0.x + this.p1.x ) ) - this.Cx;
this.Ax = this.p3.x - this.p0.x - this.Cx - this.Bx;
this.Cy = 3f * ( ( this.p0.y + this.p1.y ) - this.p0.y );
this.By = 3f * ( ( this.p3.y + this.p2.y ) - ( this.p0.y + this.p1.y ) ) - this.Cy;
this.Ay = this.p3.y - this.p0.y - this.Cy - this.By;
this.Cz = 3f * ( ( this.p0.z + this.p1.z ) - this.p0.z );
this.Bz = 3f * ( ( this.p3.z + this.p2.z ) - ( this.p0.z + this.p1.z ) ) - this.Cz;
this.Az = this.p3.z - this.p0.z - this.Cz - this.Bz;
}
// Check if p0, p1, p2 or p3 have changed
private void CheckConstant()
{
if( this.p0 != this.b0 || this.p1 != this.b1 || this.p2 != this.b2 || this.p3 != this.b3 )
{
this.SetConstant();
this.b0 = this.p0;
this.b1 = this.p1;
this.b2 = this.p2;
this.b3 = this.p3;
}
}
}
This is the Bessel computing class, a very simple calculation method.
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
public class TriangleSubdivision :MonoBehaviour{
public static int[] TriangulatePolygon (Vector2[] XZofVertices) {
//
int VertexCount = XZofVertices.Length;
//minx miny maxx maxy
float xmin = XZofVertices[0].x;
float ymin = XZofVertices[0].y;
float xmax = xmin;
float ymax = ymin;
for (int ii1 = 1; ii1 < VertexCount; ii1++)
{
if (XZofVertices[ii1].x < xmin)
{
xmin = XZofVertices[ii1].x;
}
else if (XZofVertices[ii1].x > xmax)
{
xmax = XZofVertices[ii1].x;
}
if (XZofVertices[ii1].y < ymin)
{
ymin = XZofVertices[ii1].y;
}
else if (XZofVertices[ii1].y > ymax)
{
ymax = XZofVertices[ii1].y;
}
}
float dx = xmax - xmin;
float dy = ymax - ymin;
float dmax = (dx > dy) ? dx : dy;
float xmid = (xmax + xmin) * 0.5f;
float ymid = (ymax + ymin) * 0.5f;
Vector2[] ExpandedXZ = new Vector2[3 + VertexCount];
for (int ii1 = 0; ii1 < VertexCount; ii1++)
{
ExpandedXZ[ii1] = XZofVertices[ii1];
}
ExpandedXZ[VertexCount] = new Vector2((xmid - 2 * dmax), (ymid - dmax));
ExpandedXZ[VertexCount + 1] = new Vector2(xmid, (ymid + 2 * dmax));
ExpandedXZ[VertexCount + 2] = new Vector2((xmid + 2 * dmax), (ymid - dmax));
List<Triangle> TriangleList = new List<Triangle>();
TriangleList.Add(new Triangle(VertexCount, VertexCount+1, VertexCount+2));
for (int ii1 = 0; ii1 < VertexCount; ii1++)
{
//Check triangles
List<Edge> Edges = new List<Edge>();
for (int ii2 = 0; ii2 < TriangleList.Count; ii2++)
{
if (TriangulatePolygonSubFunc_InCircle(ExpandedXZ[ii1], ExpandedXZ[TriangleList[ii2].p1],ExpandedXZ[TriangleList[ii2].p2],ExpandedXZ[TriangleList[ii2].p3]))
{
Edges.Add(new Edge(TriangleList[ii2].p1, TriangleList[ii2].p2));
Edges.Add(new Edge(TriangleList[ii2].p2, TriangleList[ii2].p3));
Edges.Add(new Edge(TriangleList[ii2].p3, TriangleList[ii2].p1));
TriangleList.RemoveAt(ii2);
ii2--;
}
}
if (ii1 >= VertexCount) { continue; }
//Judging the triangle formed by the same three points
for (int ii2 = Edges.Count - 2; ii2 >= 0; ii2--)
{
for (int ii3 = Edges.Count - 1; ii3 >= ii2 + 1; ii3--)
{
if (Edges[ii2].Equals(Edges[ii3]))
{
Edges.RemoveAt(ii3);
Edges.RemoveAt(ii2);
ii3--;
continue;
}
}
}
for (int ii2 = 0; ii2 < Edges.Count; ii2++)
{
TriangleList.Add(new Triangle(Edges[ii2].p1, Edges[ii2].p2, ii1));
}
Edges.Clear();
Edges = null;
}
//Points larger than the periphery of point set
for (int ii1 = TriangleList.Count - 1; ii1 >= 0; ii1--)
{
if (TriangleList[ii1].p1 >= VertexCount ||TriangleList[ii1].p2 >= VertexCount ||TriangleList[ii1].p3 >= VertexCount)
{
TriangleList.RemoveAt(ii1);
}
}
//Not in the room
for(int ii3 = 0;ii3<TriangleList.Count;ii3++){
if(TriangleInPolygonOuter(XZofVertices,XZofVertices[TriangleList[ii3].p1],XZofVertices[TriangleList[ii3].p2],XZofVertices[TriangleList[ii3].p3])){
TriangleList.RemoveAt(ii3);
ii3--;
}
}
TriangleList.TrimExcess();
int[] Triangles = new int[3 * TriangleList.Count];
for (int ii1 = 0; ii1 < TriangleList.Count; ii1++)
{
Triangles[3 * ii1] = TriangleList[ii1].p1;
Triangles[3 * ii1 + 1] = TriangleList[ii1].p2;
Triangles[3 * ii1 + 2] = TriangleList[ii1].p3;
}
return Triangles;
}
static bool TriangulatePolygonSubFunc_InCircle(Vector2 p, Vector2 p1, Vector2 p2, Vector2 p3) {
if (Mathf.Abs(p1.y - p2.y) < 0.0000001&&Mathf.Abs(p2.y - p3.y) < 0.0000001)
{
return false;
}
float m1, m2, mx1, mx2, my1, my2, xc, yc;
if (Mathf.Abs(p2.y - p1.y) < 0.0000001)
{
m2 = -(p3.x - p2.x) / (p3.y - p2.y);
mx2 = (p2.x + p3.x) * 0.5f;
my2 = (p2.y + p3.y) * 0.5f;
xc = (p2.x + p1.x) * 0.5f;
yc = m2 * (xc - mx2) + my2;
}
else if (Mathf.Abs(p3.y - p2.y) < 0.0000001)
{
m1 = -(p2.x - p1.x) / (p2.y - p1.y);
mx1 = (p1.x + p2.x) * 0.5f;
my1 = (p1.y + p2.y) * 0.5f;
xc = (p3.x + p2.x) * 0.5f;
yc = m1 * (xc - mx1) + my1;
}
else
{
m1 = -(p2.x - p1.x) / (p2.y - p1.y);
m2 = -(p3.x - p2.x) / (p3.y - p2.y);
mx1 = (p1.x + p2.x) * 0.5f;
mx2 = (p2.x + p3.x) * 0.5f;
my1 = (p1.y + p2.y) * 0.5f;
my2 = (p2.y + p3.y) * 0.5f;
xc = (m1 * mx1 - m2 * mx2 + my2 - my1) / (m1 - m2);
yc = m1 * (xc - mx1) + my1;
}
float dx = p2.x - xc;
float dy = p2.y - yc;
float rsqr = dx * dx + dy * dy;
dx = p.x - xc;
dy = p.y - yc;
double drsqr = dx * dx + dy * dy;
return (drsqr <= rsqr);
}
static bool TriangleInPolygonOuter(Vector2[] pList,Vector2 p1,Vector2 p2,Vector2 p3){
Vector2[] centerPoint = new Vector2[3];
centerPoint[0] = new Vector2((p1.x+p2.x)/2,(p1.y+p2.y)/2);
centerPoint[1] = new Vector2((p1.x+p3.x)/2,(p1.y+p3.y)/2);
centerPoint[2] = new Vector2((p3.x+p2.x)/2,(p3.y+p2.y)/2);
for(int j = 0,crossNum = 0;j<centerPoint.Length;j++){
for (int i = 0; i < pList.Length; i++)
{
if (IsPointInLine(centerPoint[j].x, centerPoint[j].y, pList[i].x, pList[i].y, pList[(i+1)%pList.Length].x, pList[(i+1)%pList.Length].y)==0)
{
crossNum=crossNum+1;
continue;
}else if(IsPointInLine(centerPoint[j].x, centerPoint[j].y, pList[i].x, pList[i].y, pList[(i+1)%pList.Length].x, pList[(i+1)%pList.Length].y)==2){
crossNum = 1;
break;
}
}
if ((crossNum % 2) == 0)
{
return true;
}
crossNum = 0;
}
return false;
}
//0 on the outside 1 and on the inside 2
static int IsPointInLine(float x,float y,float x1,float y1,float x2,float y2)
{
float maxY =y1;
float minY = y2;
if(y1>y2){
maxY = y1;
minY = y2;
}else{
maxY = y2;
minY = y1;
}
float averageX = (x1+x2)/2;
float averageY = (y1+y2)/2;
if(y==averageY&&x==averageX){
return 2;
}
if (y < maxY && y >minY)
{
if (x >(x1 + (x2 - x1) * (y - y1) / (y2 - y1)))
{
return 0;
}
}
return 1;
}
}
struct Triangle
{
public int p1;
public int p2;
public int p3;
public Triangle(int point1, int point2, int point3)
{
p1 = point1; p2 = point2; p3 = point3;
}
}
class Edge
{
public int p1;
public int p2;
public Edge(int point1, int point2)
{
p1 = point1; p2 = point2;
}
public Edge() : this(0, 0)
{}
public bool Equals(Edge other)
{
return ((this.p1 == other.p2) && (this.p2 == other.p1)) ||((this.p1 == other.p1) && (this.p2 == other.p2));
}
}As mentioned in the previous one of this kind, it is the class of drawing irregular figures. But in this article, I will stitch circles and irregular figures together to form figures with circular arcs. You will understand when you look at the pictures.
using UnityEngine;
using System.Collections;
public class ChartletManager : System.Object {
Bezier myBezier;
public ChartletManager(){
}
public GameObject WallChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,float height,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[52];
for(int i = 0;i<52;i++){
if(i<26){
myVertices[i] = myBezier.GetPointAtTime( (float)((i) *0.04) );
myVertices[i] = new Vector3(myVertices[i].x,myVertices[i].y,myVertices[i].z-height);
}else{
myVertices[i] = myBezier.GetPointAtTime( (float)((i-26) *0.04) );
myVertices[i] = new Vector3(myVertices[i].x,myVertices[i].y,myVertices[i].z);
}
}
myMesh.vertices = myVertices;
int[] myTriangles = new int[52 * 3];
for(int i = 0; i < 52; i++){
if(i<25){
myTriangles[i*3] = 26+i;
myTriangles[i*3+1] = i;
myTriangles[i*3+2] = i+1;
}else if(i == 25||i==51){
myTriangles[i*3] = 0;
myTriangles[i*3+1] = 0;
myTriangles[i*3+2] = 0;
}else{
myTriangles[i*3+2] = i;
myTriangles[i*3+1] = i+1;
myTriangles[i*3] = i-25;
}
}
Vector2[] myuvs = new Vector2[52];
for (int i = 0; i < 52; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = myTriangles;
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
public GameObject CircleChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[27];
myVertices[0] = new Vector3(0,0,0);
for(int i =0; i <= 25; i++)
{
myVertices[i+1] = myBezier.GetPointAtTime( (float)(i *0.04) );
}
myMesh.vertices = myVertices;
Vector2[] myuvs = new Vector2[27];
for (int i = 0; i < 27; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = TriangleSubdivision.TriangulatePolygon(myuvs);
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
public GameObject CircleAndTriangleChartletInMesh(GameObject obj,Vector3 startPoint,Vector3 endPoint,Vector3[] points,Texture2D tex,float excursion,float zoom)
{
myBezier = new Bezier( startPoint, new Vector3( excursion, zoom, 0f ), new Vector3( excursion, zoom, 0f ), endPoint);
MeshFilter myFilter = (MeshFilter)obj.GetComponent (typeof(MeshFilter));
Mesh myMesh = myFilter.mesh;
Vector3[] myVertices = new Vector3[27+points.Length];
myVertices[0] = new Vector3((startPoint.x+endPoint.x)/2,(startPoint.y+endPoint.y)/2,(startPoint.z+endPoint.z)/2);
for(int i =0; i <= 25; i++)
{
myVertices[i+1] = myBezier.GetPointAtTime( (float)(i *0.04) );
}
for(int i = 27;i<27+points.Length;i++){
myVertices[i] = points[i-27];
}
myMesh.vertices = myVertices;
Vector2[] myuvs = new Vector2[27+points.Length];
for (int i = 0; i < myuvs.Length; i++) {
myuvs [i] = new Vector2 ( (myVertices [i].x), (myVertices [i].y));
}
myMesh.triangles = TriangleSubdivision.TriangulatePolygon(myuvs);
myMesh.uv = myuvs;
myMesh.RecalculateBounds ();
myMesh.RecalculateNormals ();
obj.renderer.material.mainTexture = tex;
return obj;
}
}In order to facilitate your testing, I put my test in a class, you can directly adjust this method, I am the test, you can modify into their own scripts.
using UnityEngine;
public class MyBezier : MonoBehaviour
{
public Bezier myBezier;
public GameObject circleline;
public Texture2D tex;
void Start()
{
GameObject floorTexture = (GameObject)Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
GameObject wallTexture =(GameObject) Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
ChartletManager chartlet = new ChartletManager();
Vector3[] ceilVertices = new Vector3[4];
ceilVertices[0] = new Vector3(-4,0,0);
ceilVertices[1] = new Vector3(-4,-5,0);
ceilVertices[2] = new Vector3(4,-5,0);
ceilVertices[3] = new Vector3(4,0,0);
// ceilVertices[1] = new Vector3(-5,1,0);
// ceilVertices[2] = new Vector3(-5,-4,0);
// ceilVertices[3] = new Vector3(-2,-4.5f,0);
// ceilVertices[4] = new Vector3(-2.5f,-2,0);
// ceilVertices[5] = new Vector3(2,-2.5f,0);
// ceilVertices[6] = new Vector3(2.5f,-4,0);
// ceilVertices[7] = new Vector3(5,-4,0);
// ceilVertices[8] = new Vector3(5,0,0);
// ceilVertices[9] = new Vector3(4,0,0);
wallTexture= chartlet.WallChartletInMesh(wallTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),3.0f,tex,0,6);
floorTexture= chartlet.CircleAndTriangleChartletInMesh(floorTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),ceilVertices,tex,0,6);
}
}
Test cases, you can do what you want, Circle AndTriangle Chartlet InMesh (GameObject obj, Vector 3 start Point, Vector 3 end Point, Vector 3 [] points)
,Texture2D tex,float excursion,float zoom)
Let me explain the passing parameters of this class.
Obj is the obj object that comes in. You can use out, which can be used directly.
startPoint arc starting point
endPoint endpoint arc
Points are points of incoming irregular graphics
tex is the map.
Exceursion This is the slope of the arc.
zoom is the size of an arc, that is, the distance from the vertex of the arc to the point in the middle of the starting point and the terminating point to the normal semicircle. This value should be 1.5 times the radius of the circle.
using UnityEngine;
public class MyBezier : MonoBehaviour
{
public Bezier myBezier;
public GameObject circleline;
public Texture2D tex;
void Start()
{
GameObject floorTexture = (GameObject)Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
GameObject wallTexture =(GameObject) Instantiate(circleline,new Vector3(0,0,10),Quaternion.Euler(new Vector3(0,0,0)));
ChartletManager chartlet = new ChartletManager();
Vector3[] ceilVertices = new Vector3[10];
ceilVertices[0] = new Vector3(-4,0,0);
// ceilVertices[1] = new Vector3(-4,-5,0);
// ceilVertices[2] = new Vector3(4,-5,0);
// ceilVertices[3] = new Vector3(4,0,0);
ceilVertices[1] = new Vector3(-5,1,0);
ceilVertices[2] = new Vector3(-5,-4,0);
ceilVertices[3] = new Vector3(-2,-4.5f,0);
ceilVertices[4] = new Vector3(-2.5f,-2,0);
ceilVertices[5] = new Vector3(2,-2.5f,0);
ceilVertices[6] = new Vector3(2.5f,-4,0);
ceilVertices[7] = new Vector3(5,-4,0);
ceilVertices[8] = new Vector3(5,0,0);
ceilVertices[9] = new Vector3(4,0,0);
wallTexture= chartlet.WallChartletInMesh(wallTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),3.0f,tex,3,8);
floorTexture= chartlet.CircleAndTriangleChartletInMesh(floorTexture,new Vector3( -4f, 0f, 0f ),new Vector3( 4f, 0f, 0f ),ceilVertices,tex,3,8);
}
}
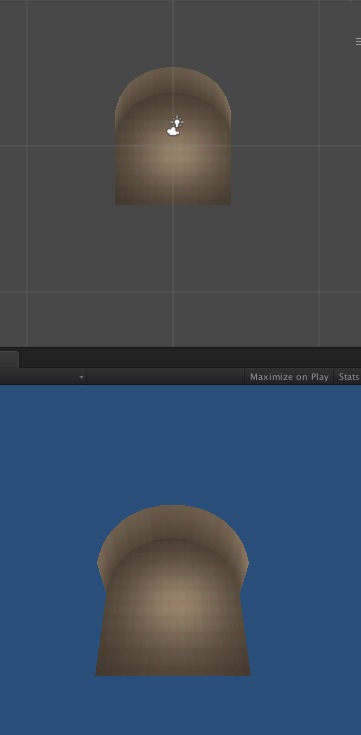
If I change the value, zoom will be inclined, of course, it can also be negative, it is concave in, excursion is negative, it will be inclined in the other direction.
This is the case in the concave, the specific situation you can test, the value range is limited, beyond, there will be an empty situation, of course, I wrote a lot of shortcomings, you can modify and modify.


I don't know why the csdn editing problem, my pictures, text and code are mixed up, so I messed up my project packed up, you can download to see the specific implementation effect.
Download address
http://download.csdn.net/detail/pzw0416/6727303
Reprinted at: https://www.cnblogs.com/riasky/p/3478873.html