6.1 example: Digital triangle

  [problem description] there is a digital triangle with layer number n (n ≤ 1000) (as shown in the figure below). There is an ant walking down from the top floor. When walking down one level, it can go down left or right. Find the maximum value of the sum of the numbers it passes through after going to the bottom layer.

 

 

  (1) Data storage

 

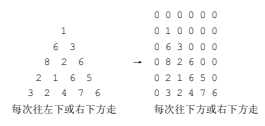
Boundary treatment:
1. There is a circle of 0 on the outermost layer, which can prevent out of bounds in the inverse method.
2. Since the right side is 0, it will not go there when making decisions.
If negative numbers are allowed, you can change 0 into a small number, or think of other methods.

  (2) Recurrence

1. Stage division: stages are divided by line, one stage for each behavior.
2. Status representation: Let f(i,j) be the maximum sum from the point on row i and column j to the starting point. All subscripts start with 1.
3. State transition equation:
 inverse: the state transition equation is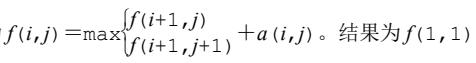

int a[N][N], f[N][N]; // a is the deformed digital triangle, and f saves the calculation results
......
for (int i=n;i>0;i--)
for (int j=1;j<=i;j++)
f[i][j] = max(f[i+1][j], f[i+1][j+1]) + a[i][j];
cout<<f[1][1];

 forward push: the state transition equation is

  Calculation sequence: first calculate a group of f[i], then calculate a group of f[i+1]... Output the results after comparison.

int a[N][N], f[N][N], result=0; // Result indicates the calculation result
......
for (int i=1;i<=n;i++)
for (int j=1;j<=i;j++)
f[i][j] = max(f[i-1][j], f[i-1][j-1]) + a[i][j];
for (int i=1;i<=n;i++) if (f[n][i]>result) result=f[n][i];
cout<<result;

(3) Memory search -- using recursion instead of recursion

If you write the state transition equation but don't know how to calculate recursively, you can use memory search.
Take the inverse state transition equation as an example:

bool visited[N][N];
// visited[i][j] indicates whether f[i][j] has been calculated.
// You can also use f[i][j]=-1 to indicate that it has not been calculated. In fact, just distinguish between "calculated" and "not calculated".
int a[N][N], f[N][N];
......
int F(int x, int y)
{
if (visited[x][y]) return f[x][y]; // If it has been calculated, the result will be returned directly. Otherwise, it will be calculated recursively.
if (x>n) return 0; // Boundary treatment
visited[x][y] = true;
return f[x][y] = max(F[i+1][j], F[i+1][j+1]) + a[i][j];
}
......
memset(visited,0,sizeof(visited));
cout<<F(1,1);

Its time complexity is o(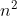), but it runs much slower than recursion.

(4) Record path

How does the maximum come from? To solve this problem, you can open another array g[N][N] to record the selection of each step. In this way, g[i][j] means "where does f(i,j) come from", or "which one of the state transition equations". Then the number on the path can be found recursively. Let's take the forward push method as an example.

int a[N][N], f[N][N], g[N][N]; // g[i][j] records "selection"
void printpath(int i, int j) // Be sure to pay attention to the order when outputting
{
if (i==0||j==0)
return;
else if (g[i][j]==1)
printpath(i-1,j);
else
printpath(i-1,j-1);
cout<<a[i][j]<<' ';
}

int result,p; // p indicates the position of the end point
for (int i=1;i<=n;i++)
{
result=p=0;
for (int j=1;j<=i;j++)
{
f[i][j] = f[i-1][j] + a[i][j];
g[i][j] = 1; // There are two options in the state transition equation, now the first.
if (f[i][j] > f[i-1][j-1] + a[i][j])
{
f[i][j] = f[i-1][j-1] + a[i][j];
g[i][j] = 2;
}
if (result > f[i][j]) result=f[i][j],p=j;
}
}
cout<<result;
printpath(n, p);

(5) Use scrolling arrays

"Space for time" is very good, but sometimes the array can't be opened at all!
During recursion, we find that although f has n rows, only two rows participate in the calculation. So you can change f into f[1][N] to save space.
When calculating, let i and i-1 take the mold of 2, that is

f[i%2][j] = max(f[(i-1)%2][j], f[(i-1)%2][j-1]) + a[i][j];

If it looks uncomfortable, it can be changed to:

#define F(i,j) f[(i)%2][j] / / note the parentheses
......
F(i,j) = max(F(i-1,j), F(i-1,j-1)) + a[i][j];

However, it is best not to use a scrolling array when the solution that requires the smallest dictionary order ① is output.

(6) Imperfect solution

If you get stuck in the dynamic programming problem during the competition and you don't want to score 0, you can consider the following methods:
① Violent search

int result = 0;
void search(int x, int y, int depth, int sum)
{
if (depth==n)
{
if (sum>result) result=sum;
return;
}
else
{
search(x+1,y,depth+1,sum + a[x+1][y]);
search(x+1,y+1,depth+1,sum + a[x+1][y+1]);
}
}

Call try(1,1,1,a[1][1]). Time complexity O(2n).
② Greed + search
For some minimum problems, the greedy algorithm can be used to obtain the better solution. Then start the search. When searching, prune as long as the calculation result is greater than the obtained minimum value. Updates the minimum value when a vertex is searched.

However, this method cannot be used for maximum problems.

③ Randomization
Starting from the top floor, make the probability of going left and right equal ①. Of course, greed can be added - making the probability in the direction of larger values higher.
Repeat this process several times and you will always get the right answer.

int result=0;
srand(time(NULL));
for (int t=1; t<=10000; t++)
{
int x=0, v=0;
for (int i=1; i<=n; i++)
{
double p=(double)rand()/(double)RAND_MAX;
if (p<0.5) x+=0; else x+=1;
v+=a[i][x];
}
if (v>result) result=v;
}