In this paper, nine sorting methods are summarized.
They are: insert sort selection sort merge sort Bubble Sort heap sort quick sort count sort cardinal sort bucket sort.
Referring to the fourth edition of Algorithms, this paper abstracts the common methods needed for sorting, and makes an abstract class. Each sorting class discussed inherits the abstract class. It only needs to pay attention to the business logic of sorting itself.
The Abstract parent class is:
abstract Sort{ abstract void sort(array); // Need to be realized void exchange(array, i, j); // Elements at i and j positions in commutative arrays boolean less(a, b); // Whether a is less than b boolean isSorted(array); // Are arrays sorted void test(arr); // Test the incoming array }
Corresponding Java implementation
/** 1. Sorting abstract classes 2. Can accept any type, you can customize the comparator 3. @param <T> */ public abstract class Sort<T> { /** Test arrays, where integer arrays are easy to use*/ protected static Integer[] testArray = { 3, 2, 5, 1, 4, 7 ,10}; /** Inheritance of this class requires sorting*/ public abstract void sort(Comparable<T>[] array); /** Business Method for Exchanging Array Elements*/ protected void exchange(Comparable<T>[] array, int i, int j){ Comparable<T> temp = array[i]; array[i] = array[j]; array[j] = temp; } /** Method of Comparing Two Elements*/ protected boolean less(Comparable<T> a, Comparable<T> b){ return a.compareTo((T) b) < 0; } /** A Method of Determining whether an Array is Sorted or not*/ protected boolean isSorted(Comparable<T>[] array){ for(int i = 1; i<array.length; i++) if(less(array[i],array[i-1])) return false; return true; } /** Testing methods, in order to facilitate the testing methods are also written into the parent class, after the completion of the subclass can be directly called to see the results.*/ protected void test(Comparable<T>[] arr){ //Array before output sorting System.out.println(Arrays.toString(arr)); //sort sort(arr); //Output sorted results System.out.println(Arrays.toString(arr)); //Has the output been sorted? System.out.println("Has it been sorted:" + isSorted(arr)); } }
1. Insertion sort
Time O(n^2); Space O(1);
Sorting time is related to input: the number of input elements, the degree of sorted input elements;
Best case: the input array is sorted and the time becomes a linear function of n.
Worst case: the input array is in reverse order and the time is a quadratic function of n
/** * Insertion sort */ public class InsertSort<T> extends Sort<T> { @Override public void sort(Comparable<T>[] array) { int len = array.length; // Insert a[i] into a[i-1], a[i-2], a[i-3]... for (int i = 1; i < len; i++) { // J starts with i, if J > 0 and the element at J is smaller than the previous element, then exchange, j--, and continue to compare. for (int j = i; j > 0 && less(array[j], array[j-1]); j--) exchange(array, j, j-1); } } public static void main(String[] args) { new InsertSort().test(testArray); } }
Result:
[3, 2, 5, 1, 4, 7, 10] [1, 2, 3, 4, 5, 7, 10] Has it been sorted: true
2. Selective Sorting
Time O(n^2), Space O(1)
Sorting time is independent of input
The best and the worst are the same.
Instability, such as {6, 6, 1}. Finding the smallest is 1, and after swapping with the first 6, the first 6 runs behind.
/** * Selection sort */ public class SelectionSort<T> extends Sort<T>{ @Override public void sort(Comparable<T>[] array) { int len = array.length; for(int i = 0; i<len; i++){ int min = i; //The left side has been ordered to find the minimum value from i+1 at a time and record the location. for(int j=i+1; j<len; j++){ if(less(array[j], array[min])) min = j; // Location of record minimum } exchange(array, min, i);//The minimum and i are exchanged after the inner loop ends to ensure that the left side is still in an ordered state } } public static void main(String[] args) { new SelectionSort().test(testArray); } }
3. Merge Sort
All merge sorting algorithms are based on the simple operation of merge, which merges two ordered arrays into a larger ordered array.
Find out the origin of this algorithm: to sort an array, you can first recursively sort it in two halves, and then merge the results.
Property: It can ensure that the array with arbitrary length of N is sorted, and the required time is proportional to NlogN.
Disadvantage: The extra space required is proportional to N.
Sorting time has nothing to do with input, and is stable at best and worst.

3.1 Top-down Merge Sorting Algorithms
/** * Merge sort: top-down * One of the most classic examples of divide-and-conquer thinking. * This recursive code is the basis of inductive proof that the algorithm can sort arrays correctly: * If it can sort two subarrays, it can sort the whole array by merging two subarrays. */ public class MergeSort<T> extends Sort<T>{ private static Comparable[] auxiliary; @Override public void sort(Comparable[] array) { auxiliary = new Comparable[array.length]; sort(array, 0, array.length-1); } private void sort(Comparable[] array, int low, int high) { if(high <= low) return; int mid = low + (high - low) / 2; sort(array, low, mid); //Sort the left half sort(array, mid + 1, high); //Sort the right half merge(array, low, mid, high);//Merging result } private void merge(Comparable[] a, int low, int mid, int high){ // Merge a[low...mid] and a[mid+1...high] int i = low, j = mid + 1; // Copy all elements into aux first, then merge them into a. for(int k = low; k <= high; k++) auxiliary[k] = a[k]; for(int k = low; k <= high; k++)//Merge back to a[low...high] if(i > mid) a[k] = auxiliary[j++]; // Use up the left half and take the right half. else if (j > high) a[k] = auxiliary[i++]; // Exhaust the right half and take the elements from the left. else if (less(auxiliary[j], auxiliary[i])) a[k] = auxiliary[j++]; // The current element on the right side is less than the current element on the left side. Take the element on the right side. else a[k] = auxiliary[i++]; // The current element on the left side is smaller than the current element on the left side. Take the element on the left side. } public static void main(String[] args) { new MergeSort().test(testArray); } }
For arrays of 16 elements, the recursion process is as follows:
The time complexity of this NLogN is not the same as that of insertion sort and selection sort. It shows that a large array can be sorted only by traversing multiple logarithmic factors of the whole array. Merge sort can be used to process millions or even larger arrays, which insert and select sort can not do.
The disadvantage is that the extra space used by auxiliary arrays is proportional to the size of N.
In addition, through some careful thinking, it can also greatly shorten the running time of merger and sorting.
Consider 1: Use insertion sort for small subarrays. Using insert sort to process small subarrays, such as arrays less than 15 in length, can generally reduce merge sort run time by 10% - 15%.
Consider 2: Test whether the array is in order. A judgment condition can be added that if array [mid]<= array [mid + 1], the array is considered ordered and the merge method is skipped, this change does not affect the recursive call of sorting, but the running time of any ordered subarray algorithm becomes linear.
Consider 3: Do not copy elements to auxiliary arrays. You can save time (but not space) by copying elements to auxiliary arrays for merging. To do this, two sorting methods need to be called, one is sorting data from the input pig to the auxiliary array, one is sorting the data from the auxiliary array to the input array.
3.2 Bottom-up Merge Sorting
Merge those mini arrays first, then pair them together to get the subarrays, and so on, until the whole array is merged together.
This implementation has less code than the standard recursive method.
First, merge in two or two, then merge in four or four, and merge in eight or eight, and go on. In each round of merging, the second subarray of the last merge may be smaller than the first one, but the merge method is not a problem. If not, the size of both arrays in all merges should be the same, and the size of the next round of neutron arrays should be doubled. As shown in the picture:
/** * Bottom-up Merge Sorting * The whole array is traversed many times and merged in pairs according to the size of the subarray. * The size of the subarray is initially 1, doubling each time. * The size of the last subarray is equal to size only if the size of the array is an even number of sizes, otherwise it will be smaller than size. * @param <T> */ public class MergeSortBU<T> extends Sort<T>{ private static Comparable[] aux; @Override public void sort(Comparable<T>[] a) { int n = a.length; aux = new Comparable[n]; //To merge lgN times in pairs for(int size = 1; size < n; size = size + size) for(int low = 0; low < n - size; low += size+size) merge(a, low, low+size-1, Math.min(low+size + size-1, n-1)); } @SuppressWarnings("unchecked") private void merge(Comparable<T>[] a, int low, int mid, int high){ int i = low, j = mid + 1; for(int k = low; k <= high; k++) aux[k] = a[k]; for(int k = low; k <= high; k++){ if(i > mid) a[k] = aux[j++]; else if(j > high) a[k] = aux[i++]; else if(less(a[j], a[i])) a[k] = aux[j++]; else a[k] = aux[i++]; } } public static void main(String[] args) { new MergeSortBU<Integer>().test(testArray); } }
If it is an array of sixteen elements sorted, the procedure is as follows
4. Bubble Sorting
Relatively simple
/** * Bubble sort * Time: O(n^2); Space O(1) * Stability, because there are two comparisons, there is no jump * Sorting time is independent of input */ public class BubbleSort<T> extends Sort<T> { @Override public void sort(Comparable[] array) { int len = array.length; for(int i = 0; i<len-1; i++){ for(int j = len-1; j>i; j--){ if(less(array[j], array[j-1])) exchange(array, j, j-1); } } } public static void main(String[] args) { new BubbleSort<Integer>().test(testArray); } }
Defects:
In the sorting process, after the first sorting, the data may have been sorted completely, but the program can not judge whether to complete the sorting, and will continue to perform the remaining (n-1-i) sorting. Solution: Set a flag bit, if there is no element exchange, then flag=0; it will never enter the second layer of the loop.
When there are more sorted data, the sorting time will be significantly prolonged, because n*(n-1)/2 times will be compared.
5. quick sort
Quick sort
It is simple to implement and suitable for various inputs. It is much faster than other algorithms in general applications.
Features: In-situ sorting (only a small auxiliary stack); time is proportional to NlgN. At the same time, it has these two advantages.
In addition, the inner loop of fast sorting is shorter than most sorting algorithms.
5.1 Basic Algorithms
Fast sorting is a divide-and-conquer algorithm, which divides an array into two sub-arrays and sorts the two parts independently.
Fast sorting and merge sorting complement each other: merge sorting divides the array into two sub-groups and sorts them separately, and merges the ordered sub-arrays into the whole array.
Quick sorting will sort arrays in such a way that when both subarrays are ordered, the whole array will naturally be ordered.
In the first case, recursive calls occur before the entire array is processed; in the second case, recursion occurs after the entire array is processed.
In merge sort, an array is divided into two halves; in fast sort, the position of segmentation depends on the content of the array.
/** * Quick sort */ public class QuickSort<T> extends Sort<T> { @Override public void sort(Comparable<T>[] array) { shuffle(array); System.out.println("After disruption:"+Arrays.toString(array)); sort(array, 0, array.length - 1); } private void sort(Comparable<T>[] array, int low, int high) { if(high <= low) return; int j = partition(array, low, high); // segmentation sort(array, low, j-1); // Sort the left half array [low,..., j-1] sort(array, j+1, high); // Sort the right half array [j + 1,..., high] } private int partition(Comparable<T>[] array, int low, int high) { // Divide the array into array [low,..., i-1], array [i], array [i+1,..., high] int i = low, j = high+1; //Left and Right Scanning Pointer Comparable v = array[low]; while(true){ //Scan around, check whether the scan is over and exchange elements while(less(array[++i], v)) if(i == high) break;//Find a position larger than v with the left pointer to the right while(less(v, array[--j])) if(j == low) break;//Find a position less than v with the right pointer to the left if(i >= j) break; // If the left pointer overlaps or exceeds the right pointer, jump out exchange(array, i, j); // Exchange elements of left and right pointer positions } exchange(array, low, j); return j; } private void shuffle(Comparable<T>[] a){ Random random = new Random(); for(int i = 0; i<a.length;i++){ int r = i + random.nextInt(a.length - i); exchange(a, i, r); } } public static void main(String[] args) { new QuickSort<Integer>().test(testArray); } }
This code is split according to the value V of array[low]. The main loop exits when pointers I and J meet. In the loop, when array[i] is less than v, when I is larger than v, a[j] is larger than v, J is reduced, and then array[i] and array[j] are exchanged to ensure that the elements on the left side of I are not greater than v, and the elements on the right side of J are not less than v. When pointers meet, the array[low] and array[j] are exchanged, and the segmentation ends, so that the segmentation value is left in array[j].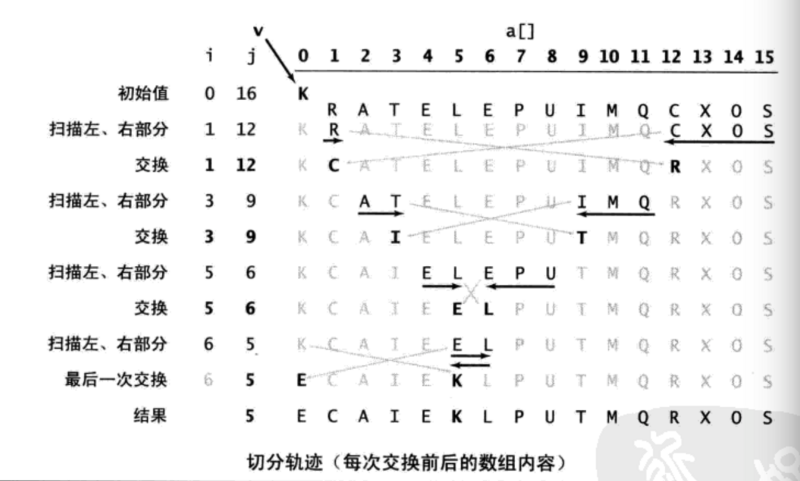
5.2 Improvement of Fast Sorting Algorithms:
If the sorting code is executed many times or is used on large arrays (especially if the properties of the sorted object array are unknown if it is published as a library function), then performance needs to be improved.
The following improvements will improve performance by 20% to 30%.
Switch to Insert Sort
For small arrays, fast sort is slower than insert sort
Because of recursion, the fast sorted ort method also calls itself in an array.
Based on these two points, fast sorting can be improved. To change the above algorithm, the statement in the sort() method is changed
if(high <= low) return ;
Replaced by:
if(high <= low + M) { Insersion.sort(array, low, high); return; }
The optimal value of the conversion parameter M is related to the system, and any value between 5 and 15 is satisfactory in most cases.
Three Sample Segmentation
Use the median of a small fraction of the elements of a subarray to cut the group. This is a better way to do segmentation, but at the cost of calculating the median.
It is found that the best method is to set the sampling size to 3 and use the elements in the middle of the sampling size.
Sampling elements can also be placed at the end of the array as sentinels to remove array boundary tests in partition().
Entropy Optimal Ordering
In the case of a large number of repetitive elements, the recursiveness of quick sorting will make subarrays of all repetitive elements appear frequently, which has great potential for improvement and can be raised to a linear level.
Simple idea: divide the array into three parts, corresponding to less than, equal to and greater than the elements of the array Yuan Shu. This segmentation is more complex than the current dichotomy.
/** * Quick Sorting: Quick Sorting of Trinomial Segmentation */ public class Quick3WaySort<T> extends Sort<T> { @Override public void sort(Comparable<T>[] array) { shuffle(array); System.out.println("After disruption:"+Arrays.toString(array)); sort(array, 0, array.length - 1); } private void sort(Comparable[] array, int low, int high) { if(high <= low) return; int lt = low, i = low + 1, gt = high; Comparable<T> v = array[low]; while(i <= gt){ int cmp = array[i].compareTo(v); if(cmp < 0) exchange(array, lt++, i++); else if(cmp > 0) exchange(array, i, gt--); else i++; } // Now array [low... lt-1] < v = a [lt... gt] < array [gt + 1.. High] is established sort(array, low, lt-1); sort(array, gt+1, high); } private void shuffle(Comparable<T>[] a){ Random random = new Random(); for(int i = 0; i<a.length;i++){ int r = i + random.nextInt(a.length - i); exchange(a, i, r); } } public static void main(String[] args) { Integer[] chars = {18,2,23,23,18,23,2,18,18,23,2,18}; new Quick3WaySort<Integer>().test(chars); } }
6. heap sort
Time complexity O(nlogn) and space complexity O(1) are in-situ sorting.
Sorting time is independent of input and unstable.
For large data processing: If top K data is selected for 10 billion pieces of data, heap sorting is used only. Heap sorting only needs to maintain a k-size space, that is, to open up a k-size space in memory.
Quick sorting is not an option because it is impossible to open up 100 billion pieces of data.
Here's a look at Section 2.4 of Algorithms Fourth Edition: Priority Queuing
Application examples: Most mobile phones give higher priority to incoming calls than other applications.
Data structure: Priority queue, need to support two operations to delete the largest element and insert elements.
This section briefly discusses the basic manifestations of priority queues, one or both of which can be performed in linear time. Then we learn the classical implementation of a middle priority queue based on binary heap structure.
Save elements with arrays and sort them according to certain conditions to achieve efficient deletion of maximum elements and insertion of elements (logarithmic level).
The heap sorting algorithm also comes from the implementation of heap-based priority queues.
Later we will learn how to construct other algorithms with priority queues.
It can also abstract some important graph search algorithms (Chapter 4 of the fourth edition of the algorithm).
A data compression algorithm can also be developed (Chapter 5 of the fourth edition of the algorithm).
Design of 6.1API
The three constructors allow the use case to construct a priority queue of size and initialize it with a given array.
Another class, MinPQ, is used where appropriate, similar to MaxPQ, except that it contains a delMin() method to delete and return the smallest element.
Any implementation of MaxPQ can easily be translated into the implementation of MinPQ, and vice versa, just change the direction of less() comparison.
Call example of priority queue
In order to demonstrate the value of priority queues, consider the problem: input N strings, each string corresponds to an integer, find the largest or smallest M integers (and their associated strings).
For example: enter financial transactions, find the largest ones; pesticide content in agricultural products, find the smallest ones...
In some scenarios, the input may be huge, or even infinite.
To solve this problem,
One way is to sort the input and find the M largest elements.
Another approach is to compare each new input with the known M largest elements, but unless M is small, this comparison is expensive.
With priority queues, this is the positive solution, as long as insert and delMin methods are implemented efficiently.
Cost of three methods:

Look at a use case for a priority queue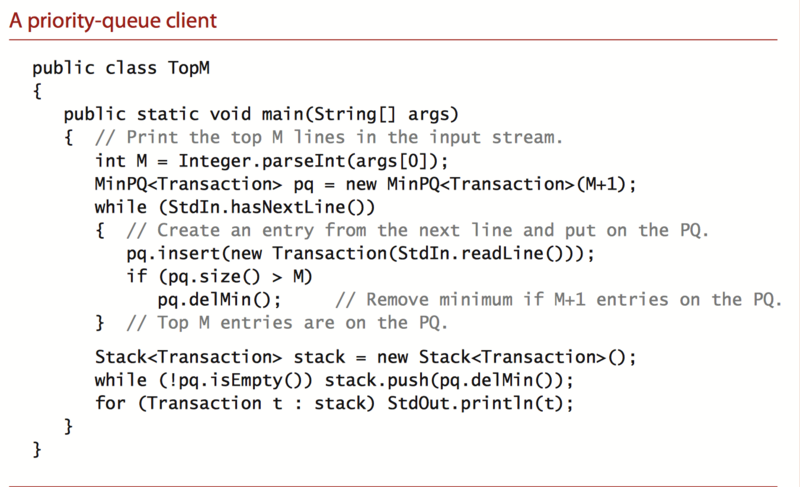
The command line enters an integer M and a series of strings, each representing a transaction. The code calls MinPQ and prints the largest number of M lines.
Primary implementation: Ordered arrays, disordered arrays, linked lists can be used.
Definition of heap: Binary heap can realize the basic operation of priority queue very well.
When each node of a binary tree is greater than or equal to its two sub-nodes, it is called heap ordering.
The root node is the largest node in the ordered binary tree of the heap.
Binary heap: A set of elements that can be sorted by a heap-ordered complete binary tree and stored hierarchically in an array (without using the zero position of the array)
In a heap, the parent node of location K is K/2 downward rounded, and the two child nodes are 2K and 2K+1, respectively. This allows you to move up and down the tree by calculating the index of the array without needing a pointer: from a[k] to the upper level, k = k/2, and from the next level, k = 2k or 2K + 1.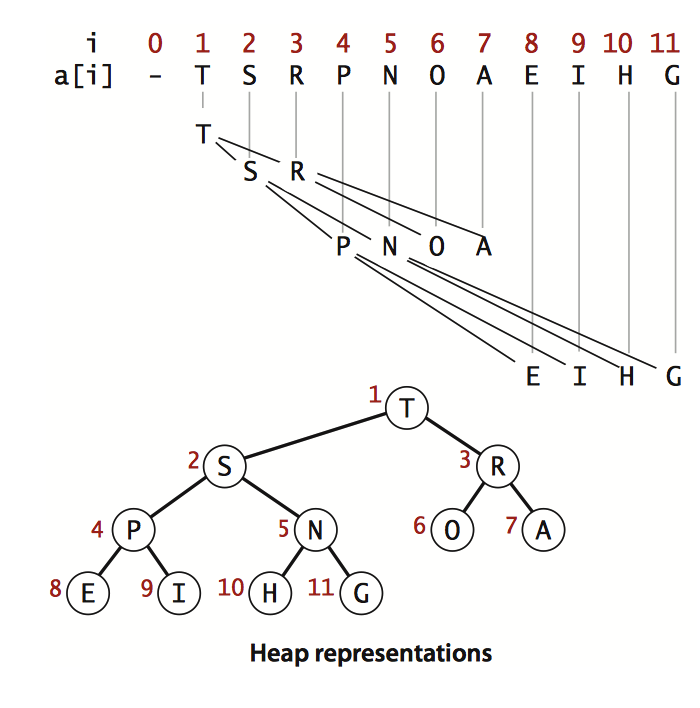
The complete binary tree implemented with arrays has a strict structure, but its flexibility is enough to enable us to efficiently implement priority queues.
It can insert elements at logarithmic level and delete the largest elements. The performance of logarithmic complexity is guaranteed by traversing arrays up and down the tree without needing pointers and the following properties.
Proposition: The height of a complete binary tree with the size of N is lgN downward rounding.
The heap algorithm:
A private array pq [] of length N+1 is used to represent a heap of size N. Instead of using pq[0], elements are placed in pq[1] - pq[n].
In previous sorting, elements were accessed through auxiliary functions less and exchange functions, but because all elements are in array pq, the implementation no longer passes arrays as parameters in order to be more compact.
The operation of the heap first makes some simple changes to break the state of the heap, then traverses the heap and restores the state of the heap as required. This process is called heap reheaping.
Methods of comparison and exchange:
Two possible scenarios:
From bottom to top heap ordering (floating)
If the ordered state of the heap is broken because a node becomes larger than its parent node, the heap needs to be repaired by exchanging its location with the parent node. After switching, the node is larger than its two children, but it may still be larger than its current parent node. It can restore order again and again in the same way. The node moves up until it meets a larger parent node. As long as you remember that the parent of the node in position K is K/2, the process is simple to implement.
Top-down heap ordering (sinking)
If the ordered state is broken because a node becomes smaller than two or one of the sub-nodes, then the ordered state can be restored by swapping it with the larger of the two sub-nodes. Switching may continue to break the orderly state out of the child nodes, so it needs to be repaired in the same way constantly, moving the node downward until its child nodes are smaller or reach the right level. The code can be implemented by locating the sub-nodes of the nodes in position K at 2K and 2K+1.
Example: You can imagine that heap is a tight underworld organization, each child node represents a subordinate, and the parent node represents its direct superior. swim means that a competent newcomer joins the organization and is promoted step by step (stepping on incompetent superiors) until he meets a stronger leader. Sik is similar to the leader of the whole community who retires and is replaced by outsiders. If his subordinates are stronger than him, their roles will change, and the exchange will continue until he is more capable than other subordinates.
The sink and swim methods are the basis for efficient implementation of priority queue API.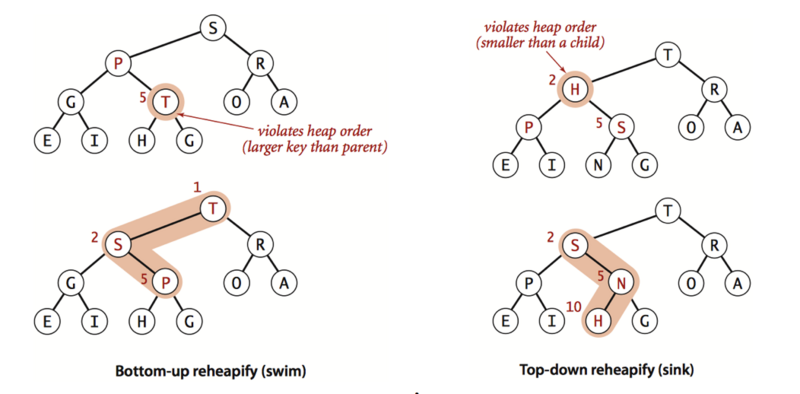
Insert elements: new elements are added to the end of the array; heap size is increased; new elements float to the appropriate position.
Delete the largest element: Delete the largest element from the top of the array; put the last element of the array at the top; reduce the size of the heap; and let the element sink to the appropriate location.
The implementation of API ensures that the operation time and queue size of inserting element and deleting maximum element are logarithmic.
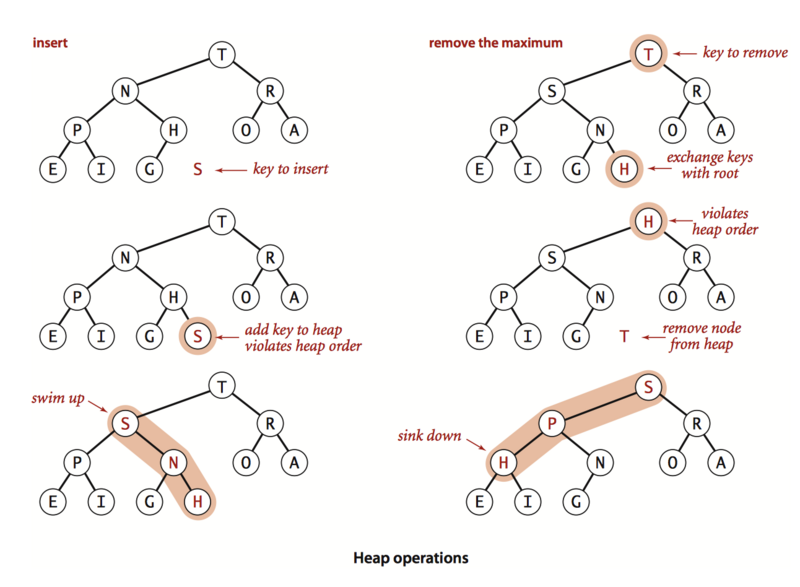
Proposition: For a heap-based priority queue with N elements, insertion of elements requires no more than lgN+1 comparison, and deletion of the largest element requires no more than 2lgN comparison. Both operations need to move elements between the root node and the bottom of the heap, and the path length does not exceed lgN. For each node on the path, deleting the largest element requires two comparisons (except the heap bottom element), one to find the larger child node, and one to determine whether the child node needs to float.
Multistacks
Constructing Complete Trident Tree Structure
Adjust array sizeAdd a parametric constructor, add code to double the array in insert, and add code to halve the length of the array in delMax.
Invariability of ElementsPriority queues store objects created by use cases, but assume that the use case code does not change them. This assumption can be translated into a mandatory condition, but increasing the complexity of the code can degrade performance.
Index priority queue
In many applications, it is necessary to allow use cases to refer to elements that have entered the priority queue.
A simple way to do this is to index each element.
In addition, a common case is that the use case already has multiple elements with a total amount of N, and may also use multiple parallel arrays to store the information of these elements at the same time. At this point, other unrelated use case code may already be using an integer index to refer to these elements.
These considerations led us to design the following API s.

Think of it as an array that can quickly access the smallest elements.
In fact, it's better to be able to quickly access the smallest elements in a particular subset of an array (all inserted elements).
Let me put it another way:
The IndexMinPQ class priority queue named pq can be considered as a representation of some elements in the array pq[0...n-1].
Think of pq.insert(k,item) as adding K to this subset and making pq[k]=item.
pq.change(k, item) represents the order pq[k]=item.
These two operations do not change the data structure on which other operations depend, the most important of which are delMin() (deleting the smallest element and returning its index) and change() (changing the index of an element in the data structure - that is, pq[i]=item). These operations are important in many applications and rely on references to elements (indexing)
Proposition: In an index priority queue of size N, the number of comparisons required for insert, change of priority, delete and remove the minimum are proportional to lgN.

This is the source code in the library.
/** * Index Priority Queue IndexMinPQ */ public class IndexMinPQ<Key extends Comparable<Key>> implements Iterable<Integer> { private int maxN; // maximum number of elements on PQ private int n; // number of elements on PQ private int[] pq; // binary heap using 1-based indexing private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i private Key[] keys; // keys[i] = priority of i public IndexMinPQ(int maxN) { this.maxN = maxN; n = 0; keys = (Key[]) new Comparable[maxN + 1]; // make this of length maxN?? pq = new int[maxN + 1]; qp = new int[maxN + 1]; // make this of length maxN?? for (int i = 0; i <= maxN; i++) qp[i] = -1; } public boolean isEmpty() {return n == 0;} public boolean contains(int i) {return qp[i] != -1;} public int size() { return n;} public void insert(int i, Key key) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (contains(i)) throw new IllegalArgumentException("index is already in the priority queue"); n++; qp[i] = n; pq[n] = i; keys[i] = key; swim(n); } public int minIndex() { if (n == 0) throw new NoSuchElementException("Priority queue underflow"); return pq[1]; } public Key minKey() { if (n == 0) throw new NoSuchElementException("Priority queue underflow"); return keys[pq[1]]; } public int delMin() { if (n == 0) throw new NoSuchElementException("Priority queue underflow"); int min = pq[1]; exch(1, n--); sink(1); assert min == pq[n+1]; qp[min] = -1; // delete keys[min] = null; // to help with garbage collection pq[n+1] = -1; // not needed return min; } public Key keyOf(int i) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue"); else return keys[i]; } public void changeKey(int i, Key key) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue"); keys[i] = key; swim(qp[i]); sink(qp[i]); } public void decreaseKey(int i, Key key) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue"); if (keys[i].compareTo(key) <= 0) throw new IllegalArgumentException("Calling decreaseKey() with given argument would not strictly decrease the key"); keys[i] = key; swim(qp[i]); } public void increaseKey(int i, Key key) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue"); if (keys[i].compareTo(key) >= 0) throw new IllegalArgumentException("Calling increaseKey() with given argument would not strictly increase the key"); keys[i] = key; sink(qp[i]); } public void delete(int i) { if (i < 0 || i >= maxN) throw new IndexOutOfBoundsException(); if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue"); int index = qp[i]; exch(index, n--); swim(index); sink(index); keys[i] = null; qp[i] = -1; } private boolean greater(int i, int j) {return keys[pq[i]].compareTo(keys[pq[j]]) > 0;} private void exch(int i, int j) { int swap = pq[i]; pq[i] = pq[j]; pq[j] = swap; qp[pq[i]] = i; qp[pq[j]] = j; } private void swim(int k) { while (k > 1 && greater(k/2, k)) { exch(k, k/2); k = k/2; } } private void sink(int k) { while (2*k <= n) { int j = 2*k; if (j < n && greater(j, j+1)) j++; if (!greater(k, j)) break; exch(k, j); k = j; } } public Iterator<Integer> iterator() { return new HeapIterator(); } private class HeapIterator implements Iterator<Integer> { // create a new pq private IndexMinPQ<Key> copy; // add all elements to copy of heap // takes linear time since already in heap order so no keys move public HeapIterator() { copy = new IndexMinPQ<Key>(pq.length - 1); for (int i = 1; i <= n; i++) copy.insert(pq[i], keys[pq[i]]); } public boolean hasNext() { return !copy.isEmpty(); } public void remove() { throw new UnsupportedOperationException(); } public Integer next() { if (!hasNext()) throw new NoSuchElementException(); return copy.delMin(); } } public static void main(String[] args) { // insert a bunch of strings String[] strings = { "it", "was", "the", "best", "of", "times", "it", "was", "the", "worst" }; IndexMinPQ<String> pq = new IndexMinPQ<String>(strings.length); for (int i = 0; i < strings.length; i++) pq.insert(i, strings[i]); // delete and print each key while (!pq.isEmpty()) { int i = pq.delMin(); StdOut.println(i + " " + strings[i]); } StdOut.println(); // reinsert the same strings for (int i = 0; i < strings.length; i++) pq.insert(i, strings[i]); // print each key using the iterator for (int i : pq) StdOut.println(i + " " + strings[i]); } }
Index priority queue use cases:
Multidirectional merging problem: merging multiple ordered input streams into an ordered input stream.
The input stream may come from multiple outputs (sorted by time).
Or a list of information from multiple music or film websites (sorted by name or artist name)
Or business transactions (sorted by account or time).
If you have enough space, you can simply read an array and sort it, but with a priority queue, you can read it all and sort it no matter how long the input is.
/** * Multiple Merges Using Priority Queues */ public class Multiway { public static void merge(In[] streams){ int n = streams.length; IndexMinPQ<String> pq = new IndexMinPQ<String>(n); for(int i = 0;i<n;i++){ if(!streams[i].isEmpty()){ String s = streams[i].readString(); pq.insert(i, s); } } while(!pq.isEmpty()){ StdOut.print(pq.minKey()+" "); int i = pq.delMin(); if(!streams[i].isEmpty()){ String s = streams[i].readString(); pq.insert(i, s); } } } public static void main(String[] args) { ClassLoader loader = Multiway.class.getClassLoader(); String dir = Multiway.class.getPackage().getName().replace(".", "/"); String path0 = loader.getResource(dir+"/m1.txt").getPath(); String path1 = loader.getResource(dir+"/m2.txt").getPath(); String path2 = loader.getResource(dir+"/m3.txt").getPath(); String[] paths = {path0, path1, path2}; int n = 3; In[] streams = new In[n]; for(int i = 0;i<n;i++){ streams[i] = new In(new File(paths[i])); } merge(streams); } }
Result A A B B B C D E F F G H I I J N P Q Q Z
As a result, with the above extended knowledge, let's look at heap sorting:
Any priority queue can be transformed into a sort method. Insert all elements into a priority queue to find the smallest elements, and then repeat the call to delete the smallest elements in order to delete them.
Heap sorting is divided into two stages. In the construction stage, the original array is reorganized into a heap, and then in the sink sorting stage, all elements are extracted from the heap in descending order and the sorting results are obtained.
For sorting purposes, instead of hiding the specific representation of priority queues, swim and sink operations will be used directly. This allows the sorted array itself to be used as the heap when sorting, so no additional space is required.
/** * Heap sort */ public class HeapSort { public static void sort(Comparable[] a){ int n = a.length - 1; // The location of index=0 is not used. n is the last index buildHeap(a, n); while(n>1){ exchange(a,1,n--); sink(a,1,n); } } /** * Structural pile */ private static void buildHeap(Comparable[] a, int n) { for(int k = n/2; k>=1; k--) sink(a, k, n); } private static void exchange(Comparable[] a, int i, int j) { Comparable temp = a[i]; a[i] = a[j]; a[j] = temp; } private static void sink(Comparable[] a, int k, int n) { while(2*k <= n){ int j = 2*k; if(j<n && less(a,j,j+1)) j++; if(!less(a,k,j)) break; exchange(a,k,j); k = j; } } private static boolean less(Comparable[] a, int i, int j){ return a[i].compareTo(a[j])<0; } public static void main(String[] args) { // The location of index=0 is not used String[] strings = { " ", "s","o", "r", "t", "e", "x", "a", "m", "p", "l", "e" }; sort(strings); System.out.println(Arrays.toString(strings)); } }
Result:
[ , a, e, e, l, m, o, p, r, s, t, x]
The algorithm uses sink method to sort elements from a[1] to a[n] (n=len-1), and the parameters accepted by sink need to be modified.
for loop construction heap, while loop exchanges the maximum elements a[1] and a[n] and repairs the heap, repeating this until the heap becomes empty
When exchange is invoked, the index is reduced by one.
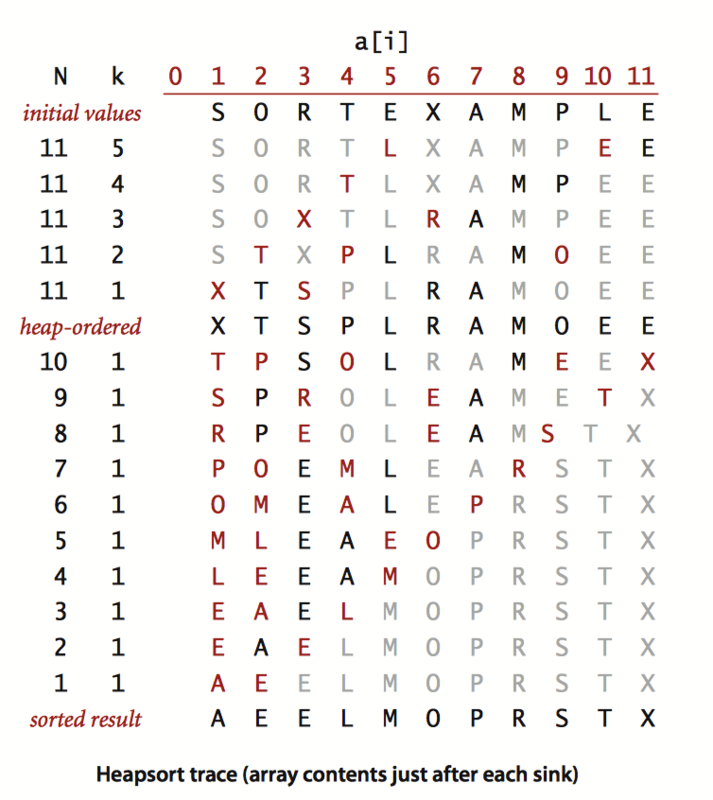
The following figure shows the structure and sinking process of the reactor: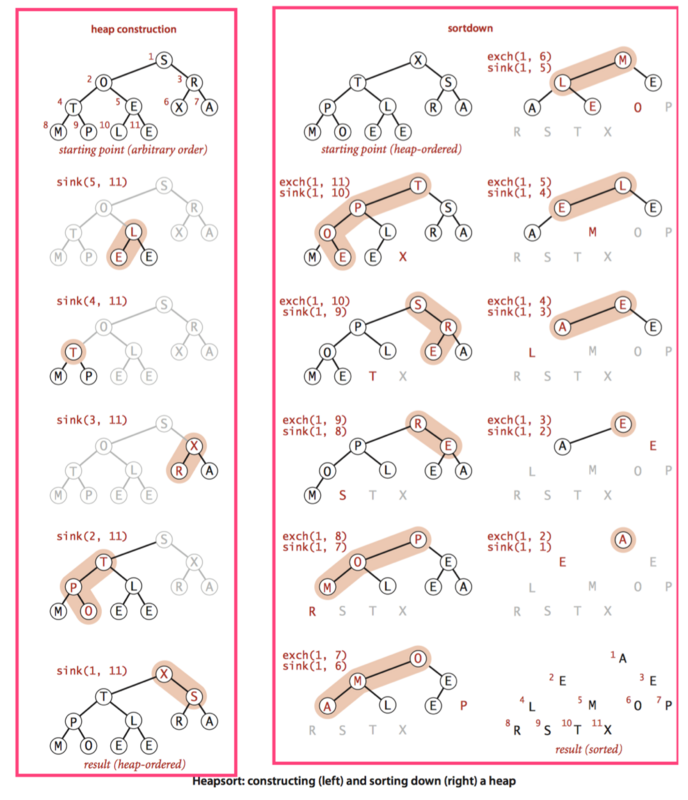
The main work of heap sorting is completed in the second stage.
Delete the largest element in the heap
The position where the array is empty after the heap is shrunk.
Undertake sinking operation.
Proposition R: It only takes less than 2N comparisons and less than N exchanges to construct a heap from N elements by sinking operation.
Proposition S: Sorting N elements requires less than (2NlgN+2N) comparisons (and half of the exchanges).
The first for loop constructs the heap, and the second while loop destroys the heap in the sink sort. All of them are based on sink method.
The API of the implementation and the priority queue is separated to highlight the simplicity of the sorting algorithm, which requires only a few lines of code to construct and sink, respectively.
Heap sorting plays an important role in the study of sorting complexity. It is the only known method that can make the best use of space and time at the same time.
In the worst case, 2NlgN comparisons and constant extra space can also be guaranteed. It's popular when space is tight.
But many applications in modern systems seldom use it because it can't take advantage of caching. Array elements are rarely compared with adjacent elements, so caching Miss is much higher than most algorithms that compare between adjacent elements.
The above sorting methods are based on comparative sorting algorithm. The lower bound of time complexity is O(nlogn)
The following three sorting algorithms are non-comparison-based. Count sort, bucket sort, cardinal sort. It can break through the lower bound of O(nlogn).
However, non-comparison-based sorting algorithms have more limitations.
Enumeration sorting ranks smaller integers and requires that the data size of sorting should not be too large.
Cardinal sorting can sort long integers, but it is not applicable to floating-point numbers.
Bucket sorting can sort floating-point numbers
Let's learn one by one.
7. Counting Sort
If you know its position when sorting, scan it again and place it in the correct position. So you just need to know how wide it is. This is the idea of counting and sorting.
Performance: Time complexity O(n+k), linear time, and stability!
Advantages: Without comparison, using address offset, the best choice for integer sorting with fixed range [0,k]. Is the fastest sorting algorithm for sorting strings
Disadvantage: The length of the array used to count depends on the range of data in the array with sorting (equal to the difference between the maximum and minimum values of the array to be sorted plus 1), which makes the sorting of counts a lot of time and space for arrays with a large range of data.
/** * Counting sort */ public class CountSort { public static int[] sort(int[] array){ int[] result = new int[array.length]; // Storage results int max = max(array); // Find the maximum max in the array to be sorted int[] temp = new int[max+1]; // Apply for an auxiliary array of size max+1 for(int i = 0; i<array.length;i++) // Traversing arrays to be sorted temp[array[i]] = temp[array[i]] + 1; //With the current value as the index, the value of the index position of the auxiliary array is increased by 1. for(int i = 1; i<temp.length;i++) // The auxiliary array traverses from index=1 temp[i] = temp[i] + temp[i-1]; // The current value + the value of the previous element is assigned to the current value. To help calculate where result is placed // Inverse Output Ensure Stability--Ensure the Relative Order of the Same Factors for(int i = array.length - 1; i>=0; i--){ int v = array[i]; // Current element result[temp[v] - 1] = v; // The current element is used as an index to get the auxiliary array element, and the result subtracted by one is used as the index in result, where the current traversal element is placed. temp[v] = temp[v] - 1; // Reduce the corresponding position of the auxiliary array by 1 for the next identical element to be indexed to the correct position } return result; } private static int max(int[] array) { int max = array[0]; for(int i = 1; i < array.length; i++) if(array[i] > max) max = array[i]; return max; } public static void main(String[] args) { int[] arr = {3,4,1,7,2,8,0}; int[] result = sort(arr); System.out.println(Arrays.toString(result)); } }
http://zh.visualgo.net/sorting
If it is difficult to understand manually, you can refer to the visualization process of the links above.
Extension: Design a n algorithm to preprocess a given n integers between 0 and k, and get how many of these n integers fall in (a,b) interval in O(1) time. The above algorithm can be used for processing, and the preprocessing time is O(n+k).
The pretreatment method in counting sort is used to preprocess auxiliary arrays so that temp[i] is not more than the number of elements I.
The number of elements in the interval (a,b) is temp[b] - temp[a]
/** * Extension of Count Sorting */ public class CountSortExt { private int[] temp; // Auxiliary array public CountSortExt(int[] a){ int max = max(a); temp = new int[max+1]; for(int i = 0; i<a.length; i++) temp[a[i]] += 1; for(int i = 1; i<temp.length; i++) temp[i] += temp[i-1]; } private int max(int[] a) { int max = a[0]; for(int cur: a) if(max < cur) max = cur; return max; } /**Returns the number of elements between (a,b)*/ public int getCountBetweenAandB(int a, int b){ return temp[b] - temp[a]; } public static void main(String[] args) { int[] arr = {1,2,2,3,2,8,0}; CountSortExt e = new CountSortExt(arr); System.out.println(e.getCountBetweenAandB(1, 8)); } }
The result is:
5
8. bucket sorting
Reference resources http://www.growingwiththeweb....
Use scenarios: Input arrays to be sorted are evenly distributed over a range.
Complexity:
When is the best case?
The extra space for O(n+k) is not a problem.
The usage scenario mentioned above: Input arrays are evenly distributed over a range.
So when is the worst?All elements of the array go into the same bucket.
/** * Bucket sorting */ public class BucketSort { private static final int DEFAULT_BUCKET_SIZE = 5; public static void sort(Integer[] array){ sort(array, DEFAULT_BUCKET_SIZE); } public static void sort(Integer[] array, int size) { if(array == null || array.length == 0) return; // Finding the Maximum and Minimum int min = array[0], max = array[0]; for(int i=1; i<array.length; i++){ if(array[i]<min) min = array[i]; else if(array[i] > max) max = array[i]; } // Initialization bucket int bucketCount = (max - min) / size + 1; List<List<Integer>> buckets = new ArrayList<>(bucketCount); for(int i = 0; i < bucketCount; i++) buckets.add(new ArrayList<Integer>()); // Distribute input arrays evenly into buckets for(int i = 0; i<array.length; i++){ int current = array[i]; int index = (current - min) / size; buckets.get(index).add(current); } // Sort each bucket and put the data in each bucket back into the array int currentIndex = 0; for(int i = 0; i < buckets.size(); i++){ List<Integer> currentBucket = buckets.get(i); Integer[] bucketArray = new Integer[currentBucket.size()]; bucketArray = currentBucket.toArray(bucketArray); Arrays.sort(bucketArray); for(int j = 0; j< bucketArray.length; j++) array[currentIndex++] = bucketArray[j]; } } public static void main(String[] args) { Integer[] array = {3,213,3,4,5,32,3,88,10}; sort(array); System.out.println(Arrays.toString(array)); } }
[3, 3, 3, 4, 5, 10, 32, 88, 213]
9. Cardinal Sorting
The principle of non-comparative integer sorting algorithm is to cut integers bitwise into different numbers, and then compare them separately according to each digit. Because integers can also express strings (such as names or dates) and floating-point numbers in a specific format, cardinal sorting is not only applicable to integers.
Realization: Unify all the values to be compared (positive integers) into the same digit length, fill in the zero before the shorter digits, and then sort them one by one from the lowest bit, so that the sequence becomes ordered from the lowest bit to the highest bit.
Implement reference links:
http://www.growingwiththeweb....
The cardinal sorting is based on LSD(Least significant digit), starting with the lowest valid keyword. First, all data are sorted by secondary keywords, and then all data are sorted by primary keywords.
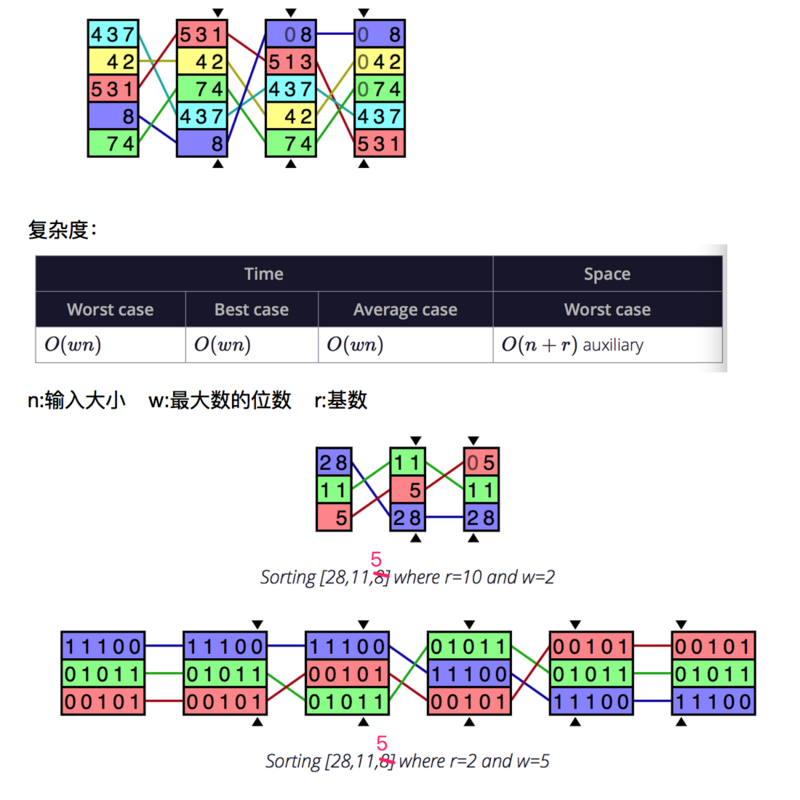
/** * Radix sorting */ public class RadixSort { public static void sort(Integer[] array){ sort(array, 10); } private static void sort(Integer[] array, int radix) { if(array == null || array.length == 0) return; // Finding the Maximum and Minimum int min = array[0], max = array[0]; for(int i = 1; i<array.length; i++){ if(array[i] < min) min = array[i]; else if(array[i] > max) max = array[i]; } int exponent = 1; int off = max - min; // Count and sort each bit while(off / exponent >= 1){ countingSortByDigit(array, radix, exponent, min); exponent *= radix; } } private static void countingSortByDigit(Integer[] array, int radix, int exponent, int min) { int bucketIndex; int[] buckets = new int[radix]; int[] output = new int[array.length]; // Initialization bucket for(int i=0; i<radix; i++) buckets[i] = 0; // Statistical frequency for(int i = 0; i<array.length; i++){ bucketIndex = (int)(((array[i] - min) / exponent) % radix); buckets[bucketIndex]++; } // Statistics for(int i = 1; i< radix; i++) buckets[i] += buckets[i-1]; // Mobile record for(int i = array.length - 1; i>=0; i--){ bucketIndex = (int)(((array[i] - min) / exponent) % radix); output[--buckets[bucketIndex]] = array[i]; } // Copy back for(int i =0; i<array.length;i++){ array[i] = output[i]; } } public static void main(String[] args) { Integer[] array = {312,213,43,4,52,32,3,88,101}; sort(array); System.out.println(Arrays.toString(array)); } }
Let's conclude here.