UFLDL is an early in-depth learning introduction written by Wu Enda's team. The rhythm of theory and practice is very good. Every time I want to read the theory quickly and write the exercises, because he helps you to complete the whole code framework and has detailed annotations, so we just need to implement a little bit of core coding work. Come on, get started!

Some people also have translations of this article. Let's have a look at it.

Section 3 is Vectorization.

The idea of this section is to use vector programming thinking to make the code run more efficiently, rather than using for loops. So after this time, I saw the symbol sum and I thought for the first time whether I could use vector programming.

To use vector programming, it is better to write one or two summation items, and then use matrix multiplication similar to the inner product to express, the tutorial is not too clear, you can use matrix multiplication to express it, just pay attention to the corresponding dimension of the matrix!!

Of course, I have learned a function that I will often use later: bsxfun function, which is used for element-wise operation, that is, the corresponding operation between vector elements. See the official document of matlab for details!

Following is my code for linear regression and logical regression that I wrote before using vectorization (annotate the corresponding non-vectorized invocation statement at run time):

What I use here is: matlab 2016a

linear_regression_vec.m:

function [f,g] = linear_regression_vec(theta, X,y)
  %
  % Arguments:
  %   theta - A vector containing the parameter values to optimize.
  %   X - The examples stored in a matrix.
  %       X(i,j) is the i'th coordinate of the j'th example.
  %   y - The target value for each example.  y(j) is the target for example j.
  %
  m=size(X,2);
  
  % initialize objective value and gradient.
%   f = 0;
%   g = zeros(size(theta));

  %
  % TODO:  Compute the linear regression objective function and gradient 
  %        using vectorized code.  (It will be just a few lines of code!)
  %        Store the objective function value in 'f', and the gradient in 'g'.
  %
%%% YOUR CODE HERE %%%
f = 0.5 .* (theta' * X - y) * (theta' * X - y)';
% g = g';
g = (theta' * X - y) * X';
g = g';

Operation results:


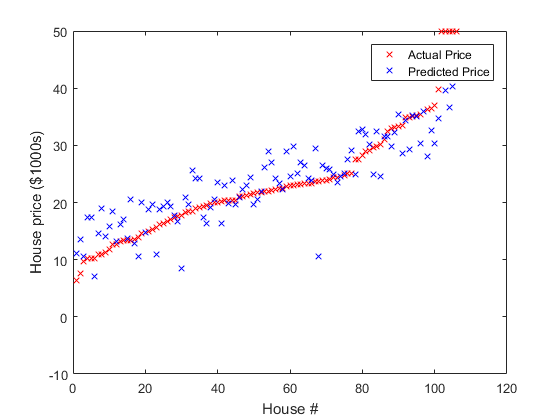
You can see and before 0.78 seconds, now there is a faster improvement!

linear_regression_vec.m:

function [f,g] = logistic_regression_vec(theta, X,y)
  %
  % Arguments:
  %   theta - A column vector containing the parameter values to optimize.
  %   X - The examples stored in a matrix.  
  %       X(i,j) is the i'th coordinate of the j'th example.
  %   y - The label for each example.  y(j) is the j'th example's label.
  %
  m=size(X,2);
  
  % initialize objective value and gradient.
  f = 0;
  g = zeros(size(theta));
  

  %
  % TODO:  Compute the logistic regression objective function and gradient 
  %        using vectorized code.  (It will be just a few lines of code!)
  %        Store the objective function value in 'f', and the gradient in 'g'.
  %
%%% YOUR CODE HERE %%%
h = inline('1./(1+exp(-z))');
% Calculate f
f = f - (y*log(h(X'*theta)) + (1-y)*log(1-h(X'*theta)));

% Calculate g
g = X * (h(theta' * X) - y)';

Operation results: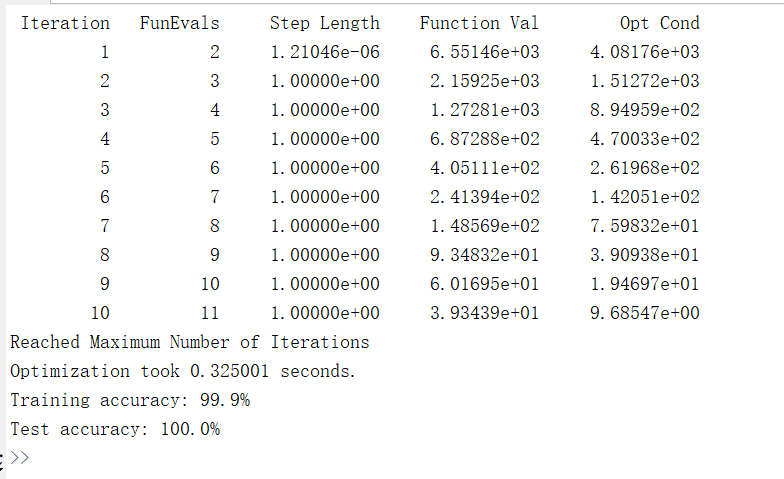

You can see that in 7.22 seconds, the speed has increased by 22 times!

Where there is a lack of understanding, please also point out that there are better ideas, you can comment and exchange below!