In the actual project development process, we often use: Vector3.Lerp(), Mathf.Lerp()... And other methods. The value returned by such methods is actually a linear growth. But many friends have made elastic growth, even not known.

1. Create corresponding objects.

1. Create two cubes named Cube one and Cube two.
2. Create a ground Plane.
3. Icon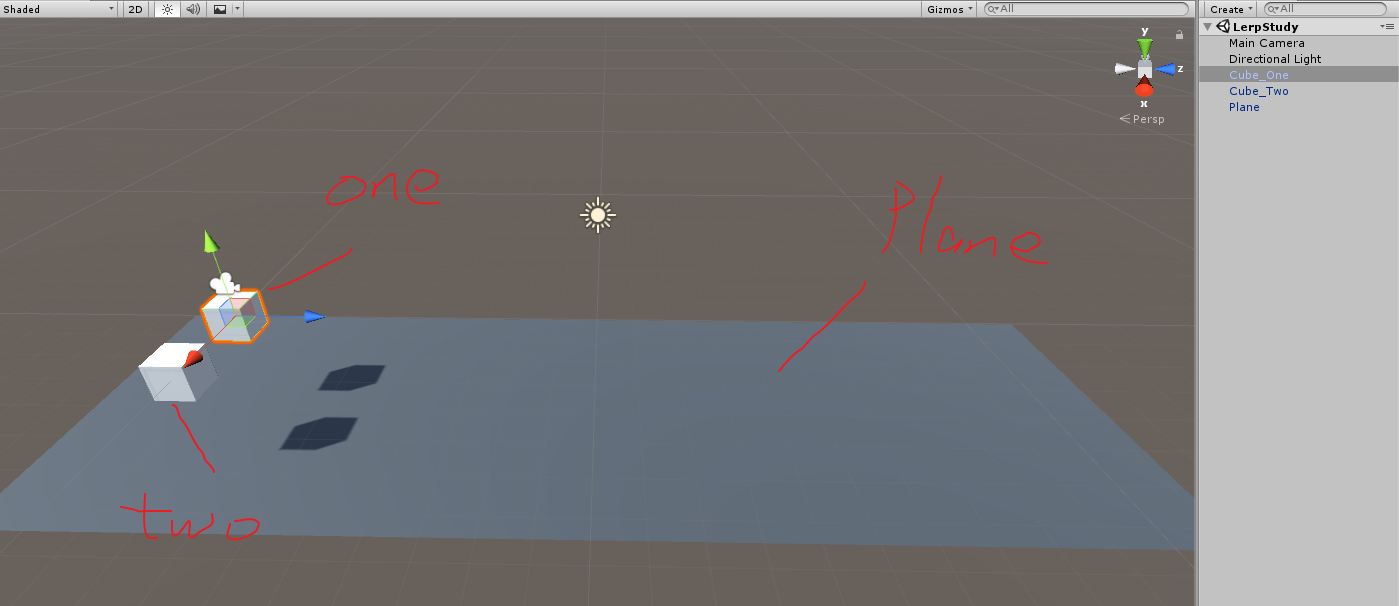

II. Create script "LerpStudy.cs"

1. Script example:

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class LerpStudy : MonoBehaviour 
{
    /// <summary>
    ///Target location
    /// </summary>
    private Vector3 m_Target;

    /// <summary>
    ///Mode 1 common speed expression
    /// </summary>
    private float m_Speed = 2.0f;

    /// <summary>
    ///Currently selected run method
    /// </summary>
    public MethodType CurrMethodType;

    /// <summary>
    ///Mode 1 common expression of time accumulation
    /// </summary>
    private float m_Time;//time

    private void Awake()
    {
        m_Target = new Vector3(transform.position.x, 0.0f, 10.0f);
    }

    private void Start()
    { }

    private void Update()
    {
        if (CurrMethodType == MethodType.One)
        {
            Method_One();
        }
        else
        {
            Method_Two();
        }
    }

    /// <summary>
    ///Wrong usage
    /// </summary>
    private void Method_One()
    {
        transform.position = Vector3.Lerp(transform.position, m_Target, Time.deltaTime * m_Speed);
        
    }

    /// <summary>
    ///The right way to use it
    /// </summary>
    private void Method_Two()
    {
        m_Time =  Time.deltaTime + m_Time;
        transform.position = Vector3.Lerp(transform.position, m_Target, m_Time * 0.05f);
    }
}

/// <summary>
///Method type
/// </summary>
public enum MethodType
{
    One,
    Two
}

2. The script has Method_One() and Method_Two() methods. Method one() is a common and wrong way to use it, and method two() is the right way to use it.
3. Mount the script to cube One and cube Two respectively, and select One for cube One's method type and Two for cube Two's method type.
4. The operation results are as follows:

5. It can be seen from the analysis that the elastic velocity of the upper cube reaches the target position, while that of the lower cube is uniform.
Remember the formula: value = a + (b - a) * t;
a is the current position
b is the target location
t is the percentage increase, and the value is between 0 and 1 (time increment can be used).