Conceptual definitions of graphs:

• Connected graph: In undirected graph, if any two vertices vivi and vjvj have paths that are connected, the undirected graph is called connected graph.
• Strongly connected graph: In a directed graph, if any two vertices vivi and vjvj have paths that are connected, the directed graph is called a strongly connected graph.
• Connected network: In a connected graph, if the edges of the graph have some meaning, each edge corresponds to a number, called weight; weight represents the cost of connecting the vertices, called connected network.
• Spanning tree: A spanning tree of a connected graph is a connected subgraph that contains all n vertices in the graph, but only enough n-1 edges to form a tree.A spanning tree with n vertices has only n-1 edges. If an additional edge is added to the spanning tree, it must become a ring.
• Minimum spanning tree: In all spanning trees of a connected network, the cost of all edges and the smallest spanning tree are called the minimum spanning tree.

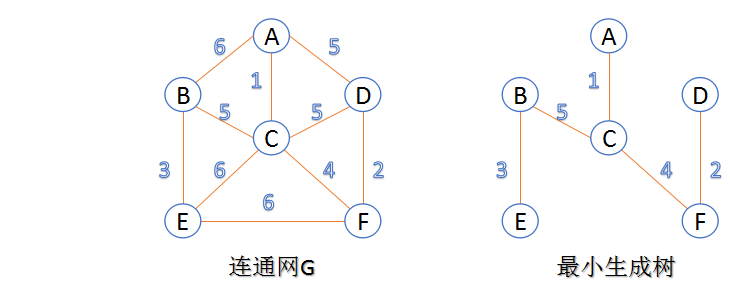
Following are two minimum spanning tree algorithms

1.Kruskal algorithm

This algorithm can be called "edge-adding". The initial minimum spanning tree edge number is 0. For each iteration, a least-cost edge that meets the criteria is selected and added to the set of edges of the minimum spanning tree.

1. Sort all edges in the graph from lowest cost to highest cost;
2. Consider the n vertices in the graph as separate forests of n trees.
3. Select edges by weight from small to large. The two vertices ui, VI ui, VI connected by the selected edge belong to two different trees, which become one edge of the smallest spanning tree and merge the two trees as one tree.
4. Repeat (3) until all vertices are within a tree or have n-1 edges.

2. Prim algorithm

This algorithm can be referred to as the "plus point" method, where each iteration selects the point corresponding to the least expensive edge and adds it to the minimum spanning tree.The algorithm starts at a vertex s and grows gradually to cover all vertices of the entire connected network.

1. The set of all vertices of the graph is VV; initial set u={s},v=V_u u={s},v=V_u;
2. Among the edges that can be composed of two sets u, V U and v, select the one with the lowest cost (u0,v0)(u0,v0), join the minimum spanning tree, and merge V0 V0 into the set U.
3. Repeat these steps until the smallest spanning tree has n-1 edges or n vertices.

Since points are constantly added to the set u, the least-cost edge must be updated synchronously; an auxiliary array closedge is needed to maintain the minimum-cost edge information for each vertex in the set v and in the set u:

struct
{
  char vertexData   //Represents vertex information in u
  UINT lowestcost   //Minimum cost
}closedge[vexCounts]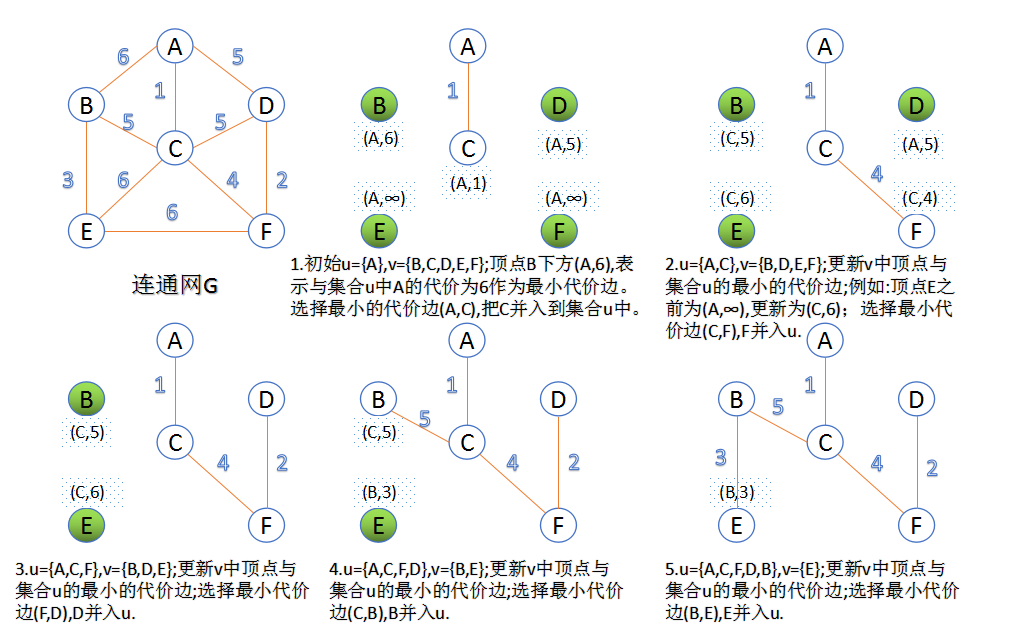

3. Full code

/************************************************************************
CSDN Do not build tall terraces in floating sand http://blog.csdn.net/luoshixian099 algorithm introduction--Minimum spanning tree (Prim, Kruskal) July 14, 2016
************************************************************************/
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define INFINITE 0xFFFFFFFF   
#Define Vertex Data unsigned int //vertex data
#define UINT  unsigned int
#define vexCounts 6 //Number of vertices
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };
struct node 
{
    VertexData data;
    unsigned int lowestcost;
}closedge[vexCounts]; //Auxiliary information in Prim algorithm
typedef struct 
{
    VertexData u;
    VertexData v;
    unsigned int cost;  //The cost of edges
}Arc;  //Edge information of the original graph
void AdjMatrix(unsigned int adjMat[][vexCounts])  //adjacency matrix
{
    for (int i = 0; i < vexCounts; i++)   //Initialize adjacency matrix
        for (int j = 0; j < vexCounts; j++)
        {
            adjMat[i][j] = INFINITE;
        }
    adjMat[0][1] = 6; adjMat[0][2] = 1; adjMat[0][3] = 5;
    adjMat[1][0] = 6; adjMat[1][2] = 5; adjMat[1][4] = 3;
    adjMat[2][0] = 1; adjMat[2][1] = 5; adjMat[2][3] = 5; adjMat[2][4] = 6; adjMat[2][5] = 4;
    adjMat[3][0] = 5; adjMat[3][2] = 5; adjMat[3][5] = 2;
    adjMat[4][1] = 3; adjMat[4][2] = 6; adjMat[4][5] = 6;
    adjMat[5][2] = 4; adjMat[5][3] = 2; adjMat[5][4] = 6;
}
int Minmum(struct node * closedge)  //Return the least-cost edge
{
    unsigned int min = INFINITE;
    int index = -1;
    for (int i = 0; i < vexCounts;i++)
    {
        if (closedge[i].lowestcost < min && closedge[i].lowestcost !=0)
        {
            min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}
void MiniSpanTree_Prim(unsigned int adjMat[][vexCounts], VertexData s)
{
    for (int i = 0; i < vexCounts;i++)
    {
        closedge[i].lowestcost = INFINITE;
    }      
    closedge[s].data = s;      //Start at vertex s
    closedge[s].lowestcost = 0;
    for (int i = 0; i < vexCounts;i++)  //Initialize auxiliary array
    {
        if (i != s)
        {
            closedge[i].data = s;
            closedge[i].lowestcost = adjMat[s][i];
        }
    }
    for (int e = 1; e <= vexCounts -1; e++)  //Exit on n-1 edges
    {
        int k = Minmum(closedge);  //Selecting the least-cost edge
        cout << vextex[closedge[k].data] << "--" << vextex[k] << endl;//Join to Minimum Spanning Tree
        closedge[k].lowestcost = 0; //Cost set to 0
        for (int i = 0; i < vexCounts;i++)  //Update vertex minimum cost edge information in v
        {
            if ( adjMat[k][i] < closedge[i].lowestcost)
            {
                closedge[i].data = k;
                closedge[i].lowestcost = adjMat[k][i];
            }
        }
    }
}
void ReadArc(unsigned int  adjMat[][vexCounts],vector<Arc> &vertexArc) //Save edge cost information of graph
{
    Arc * temp = NULL;
    for (unsigned int i = 0; i < vexCounts;i++)
    {
        for (unsigned int j = 0; j < i; j++)
        {
            if (adjMat[i][j]!=INFINITE)
            {
                temp = new Arc;
                temp->u = i;
                temp->v = j;
                temp->cost = adjMat[i][j];
                vertexArc.push_back(*temp);
            }
        }
    }
}
bool compare(Arc  A, Arc  B)
{
    return A.cost < B.cost ? true : false;
}
bool FindTree(VertexData u, VertexData v,vector<vector<VertexData> > &Tree)
{
    unsigned int index_u = INFINITE;
    unsigned int index_v = INFINITE;
    for (unsigned int i = 0; i < Tree.size();i++)  //Check which tree u and V belong to
    {
        if (find(Tree[i].begin(), Tree[i].end(), u) != Tree[i].end())
            index_u = i;
        if (find(Tree[i].begin(), Tree[i].end(), v) != Tree[i].end())
            index_v = i;
    }
 
    if (index_u != index_v)   //u,v is not on one tree, merge two trees
    {
        for (unsigned int i = 0; i < Tree[index_v].size();i++)
        {
            Tree[index_u].push_back(Tree[index_v][i]);
        }
        Tree[index_v].clear();
        return true;
    }
    return false;
}
void MiniSpanTree_Kruskal(unsigned int adjMat[][vexCounts])
{
    vector<Arc> vertexArc;
    ReadArc(adjMat, vertexArc);//Read Edge Information
    sort(vertexArc.begin(), vertexArc.end(), compare);//Edges sorted from smallest to largest
    vector<vector<VertexData> > Tree(vexCounts); //6 independent trees
    for (unsigned int i = 0; i < vexCounts; i++)
    {
        Tree[i].push_back(i);  //Initialize information for 6 independent trees
    }
    for (unsigned int i = 0; i < vertexArc.size(); i++)//Minimum cost edges, from smallest to largest
    {
        VertexData u = vertexArc[i].u;  
        VertexData v = vertexArc[i].v;
        if (FindTree(u, v, Tree))//Check if the two vertices on this side are in a tree
        {
            cout << vextex[u] << "---" << vextex[v] << endl;//Add this edge to the minimum spanning tree
        }   
    }
}
 
int main()
{
    unsigned int  adjMat[vexCounts][vexCounts] = { 0 };
    AdjMatrix(adjMat);   //adjacency matrix
    cout << "Prim :" << endl;
    MiniSpanTree_Prim(adjMat,0); //Prim algorithm, starting at vertex 0.
    cout << "-------------" << endl << "Kruskal:" << endl;
    MiniSpanTree_Kruskal(adjMat);//Kruskal algorithm
    return 0;
}