1. The attribute operations in the tree are:

1, the number of nodes in the tree, the height in the tree, and the degree of the tree;

2. Number of nodes in the tree:

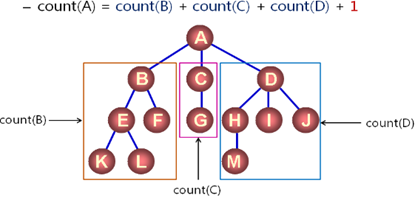
1, define function: count(node)

1. Count the number of nodes in the tree with node as the root node;

2, recursive implementation;

2. Function code implementation:

 1     /* It is very delicate to find the number of nodes of the tree represented by the node as the root node */
 2     int count(GTreeNode<T>* node) const // Publicly owned count() Function is const function
 3     {
 4         int ret = 0;
 5 
 6         if( node != NULL )  // If it is empty, it is directly the number of empty trees, 0; in the first case, if it is empty node No kids, then for Loop will not execute, return 1;
 7         {
 8             ret = 1;  // There is at least one node. In the second case
 9 
10             for(node->child.move(0); !node->child.end(); node->child.next())  // The third situation
11             {
12                 ret += count(node->child.current());  // The number of children owned by the current node, and then add up
13             }
14         }
15 
16         return ret;
17 　　}

3. Implementation of node member function code in the tree:

1 int count() const 

2 { 

3 return count(root()); 

4 }              

3. Height of tree:

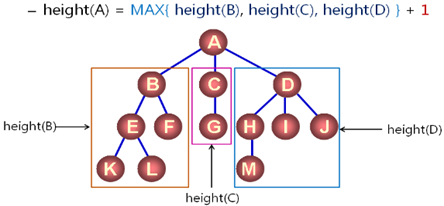
1, define function: height(node)

Get the height of the tree whose node is the root node;

2, recursive implementation;

2. Function code implementation:

 1     /* Recursive implementation of tree height with node as root node */
 2     int height(GTreeNode<T>* node) const
 3     {
 4         int ret = 0;
 5 
 6         if( node != NULL )  // Empty tree height is 0
 7         {
 8             for(node->child.move(0); !node->child.end(); node->child.next())
 9             {
10                 int h = height(node->child.current());  // Find the height of the current subtree
11 
12                 if( ret < h )  // Traverse to find the largest element
13                 {
14                     ret = h;
15                 }
16             }
17 
18             ret = ret + 1;  // The height of the subtree plus the height of the root node is the height of the current tree, including two or three cases
19         }
20 
21         return ret;
22 　　}

3. Tree height member function code implementation:

1 int height() const 

2 { 

3 return height(root()); 

4 } 

4. Degree of tree:

1, define function: degree(node)

Get the degree of the tree whose node is the root node;

2, recursive implementation;

2. The tree degree function code is implemented:

 1     /* Recursively implement the degree of tree with node as node */
 2     int degree(GTreeNode<T>* node) const
 3     {
 4         int ret = 0;
 5 
 6         if( node != NULL )  // Empty tree degree is 0
 7         {
 8             ret = node->child.length();  // Number of root children
 9 
10             for(node->child.move(0); !node->child.end(); node->child.next())
11             {
12                 int d = degree(node->child.current());  // Degree of each subtree
13 
14                 if( ret < d )  // If the current degree is small, the newly calculated degree will be saved, which also includes the number of children of the root node.
15                 {
16                     ret = d;  // ret Is the maximum degree, that is, the degree of the tree
17                 }
18             }
19         }
20 
21         return ret;
22 　　}

3, the tree degree function code is implemented:

 1     /* Recursively implement the degree of tree with node as node */
 2     int degree(GTreeNode<T>* node) const
 3     {
 4         int ret = 0;
 5 
 6         if( node != NULL )  // Empty tree degree is 0
 7         {
 8             ret = node->child.length();  // Number of root children
 9 
10             for(node->child.move(0); !node->child.end(); node->child.next())
11             {
12                 int d = degree(node->child.current());  // Degree of each subtree
13 
14                 if( ret < d )  // If the current degree is small, the newly calculated degree will be saved, which also includes the number of children of the root node
15                 {
16                     ret = d;  // ret Is the maximum degree, that is, the degree of the tree
17                 }
18             }
19         }
20 
21         return ret;
22 　　}