tree structure

Our previous studies are basically one-to-one problems, and the tree is a nonlinear data structure, which is a finite set with hierarchical relationship composed of n(n ≥ 0) nodes

characteristic:
When n=0, it is called an empty tree. In any non empty tree:

• There is and only one root node
• When n > 1, the other nodes can be divided into m (M > 0) disjoint finite sets T1, T2,... Tm. Each set itself is a tree and is called the root subtree. The root node of each subtree has and only has one precursor and can have 0 or more successors
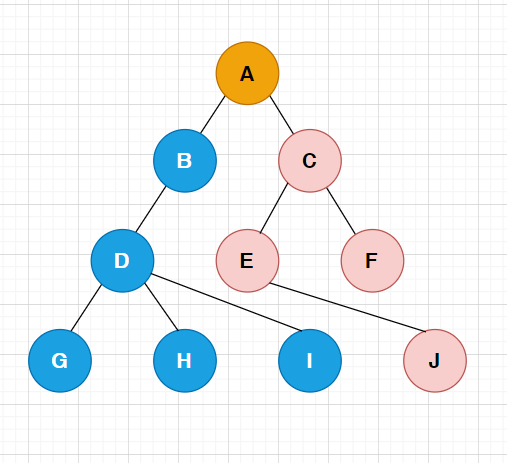
  As shown in the figure:
  .
• Trees are recursively defined

concept

name	concept
Degree of node:	The number of subtrees contained in A node is called the degree of the node; As shown in the figure above: 2 for A and 3 for D
Degree of tree:	In a tree, the degree of the largest node is called the degree of the tree; As shown in the figure above: the degree of the tree is 3
Leaf node or terminal node:	A node with a degree of 0 is called a leaf node; As shown in the figure above, nodes G, H, I, F... Are leaf nodes
Parent node or parent node:	If A node contains child nodes, the node is called the parent node of its child nodes; As shown in the figure above, A is the parent node of B
Child node or child node:	The root node of the subtree contained in a node is called the child node of the node; As shown in the figure above: B is the child node of A
Root node:	Nodes without parent nodes in A tree; As shown in the figure above: A
Hierarchy of nodes:	Starting from the definition of the root, the root is the first layer, the child node of the root is the second layer, and so on
Height or depth of the tree:	The maximum level of nodes in the tree; As shown in the figure above: the height of the tree is 4
Non terminal node or branch node:	Nodes whose degree is not 0; As shown in the figure above, nodes B, C, D, E... Are branch nodes
Sibling node:	Nodes with the same parent node are called brother nodes; As shown in the figure above, B and C are sibling nodes
Cousin node:	The nodes with parents on the same layer are cousins to each other; As shown in the figure above, D and E are brother nodes to each other
Ancestor of node:	All nodes on the branch from the root to the node; As shown in the figure above: A is the ancestor of all nodes
descendants:	Any node in the subtree with a node as the root is called the descendant of the node. As shown in the figure above: all nodes are descendants of A
forest:	The set of m(m ≥ 0) disjoint trees is called forest

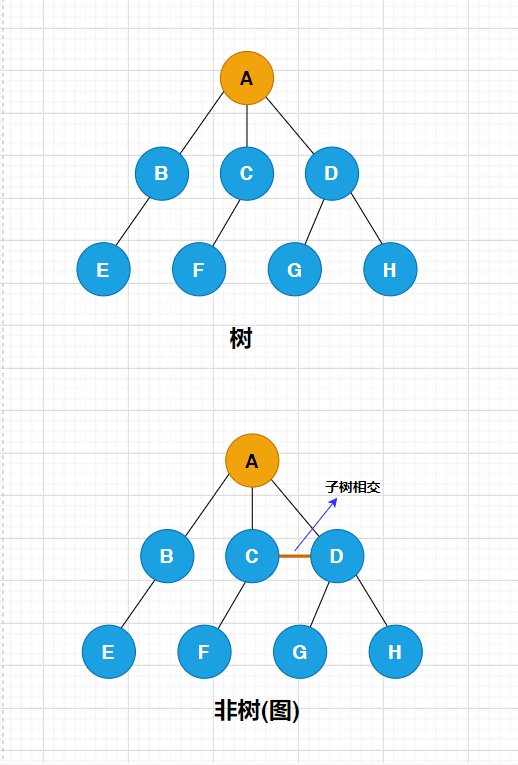
The difference between tree and non tree (graph)

• Subtrees are disjoint
• In addition to the root node, each node has one and only one parent node
• A tree with n nodes has n-1 edges

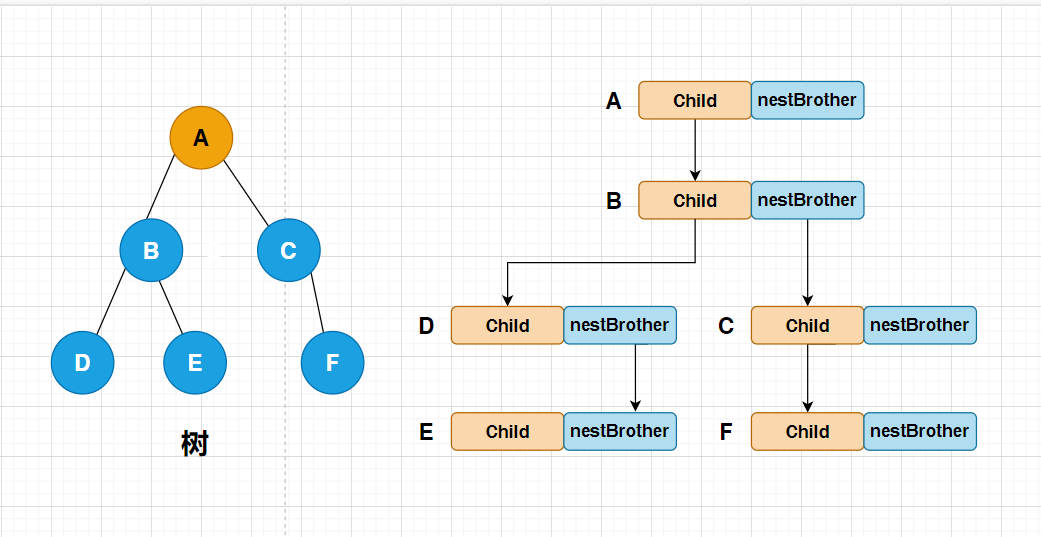
Tree representation

The most commonly used method - child brother representation:

class Node{
    int value;  //Data stored in the tree
    Node firstChild;  //First child reference in tree
    Node nextBrother; //Next brother reference
}

Draw a picture to show:

Binary tree

definition

For cases where there are two results at a certain stage, such as 0 and 1, true and false, up and down, right and wrong, positive and negative, it is suitable to model with tree structure, and this tree is a very special tree structure, which is called binary tree

A binary tree is a finite set of n(n ≥ 0) nodes. The set is either an empty set (called an empty Binary Tree) or consists of a root node and two disjoint left and right subtrees called root nodes respectively

characteristic:

• Each node can have at most two subtrees, and the degree of binary tree can exceed 2
  Note that there are not only two subtrees, but at most. It is OK to have no subtree or one subtree
• The subtree of a binary tree can be divided into left and right, and the order of its subtrees can not be reversed arbitrarily. Therefore, a binary tree is an ordered tree
• Even if a node in the tree has only one subtree, it is necessary to distinguish whether it is a left subtree or a right subtree

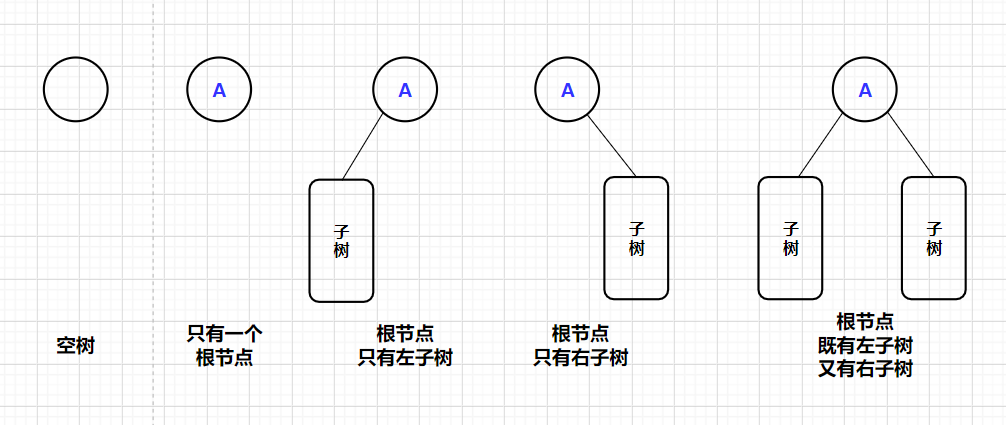
Basic form of binary tree:

• Empty binary tree
• There is only one root node
• The root node has only the left subtree
• The root node has only the right subtree
• The root node has both left and right subtrees
• 

Special binary tree:

Full binary tree:

A binary tree is full if the number of nodes in each layer reaches the maximum (i.e. 2)
The number of layers of a binary tree is n, and the total number of nodes is 2n-1

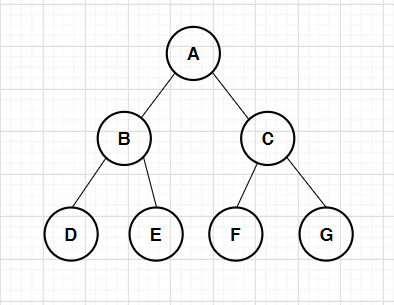
Characteristics of full binary tree:

• Leaves only appear in the lowest layer, and it is impossible to achieve balance if they appear in other layers
• The degree of a non leaf node must be 2
• In the same depth binary tree, the full binary tree has the largest number of nodes and the largest number of leaves

Complete binary tree:

Intuitively, compared with the full binary tree, a piece is missing in the small right corner of the complete binary tree

Complete binary tree is a highly efficient data structure. For a binary tree with depth K and n nodes, it is called complete binary tree if and only if each node corresponds to the nodes numbered from 1 to n in the full binary tree with depth K. full binary tree is a special complete binary tree

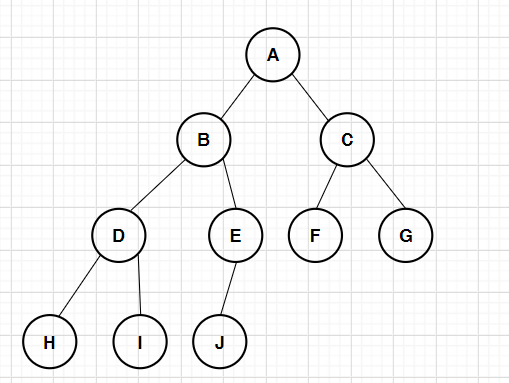
Characteristics of complete binary tree:

• Leaf nodes can only appear in the bottom two layers
• The lowest leaves must be concentrated in a continuous position on the left
• The penultimate layer, if there are leaf nodes, must appear in the continuous position on the right
• If the node degree is 1, the node has only the left subtree
• For a binary tree with the same number of nodes, the depth of a complete binary tree is the smallest

Related operations of binary tree

Representation of binary tree

It can be expressed by left and right children

class Node{
    int val;      //Stored data
    Node left;    //Reference to the root node of the left subtree
    Node right;   //Reference to the root node of the right subtree
    Node parent;  //Parent reference (optional)
}

Traversal of binary tree 🔺

Traversal: traversal accesses each element in the collection in a certain order without repetition or omission
Because the binary tree is not a linear structure, it is relatively complex to traverse

Manually construct a tree:

class Node{
    char val;      //Stored data
    Node left;    //Reference to the root node of the left subtree
    Node right;   //Reference to the root node of the right subtree
    Node parent;  //Parent reference (optional)

    //Provide construction method
    public Node(char val) {
        this.val = val;
    }
}

//Build a tree
public static Node buildTree(){
    Node a = new Node('A');
    Node b = new Node('B');
    Node c = new Node('C');
    Node d = new Node('D');
    Node e = new Node('E');
    
    a.left = b;
    a.right = c;
    b.left = d;
    b.right = e;

    return a;
}

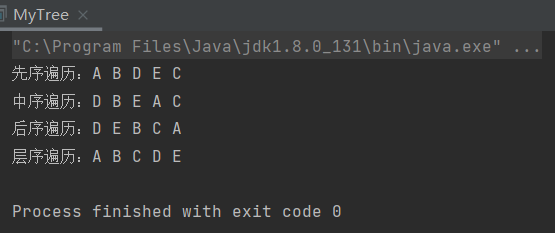
1. Preorder traversal

First visit the root node, recursively traverse the left subtree, and recursively traverse the right subtree (around the root)

Example:

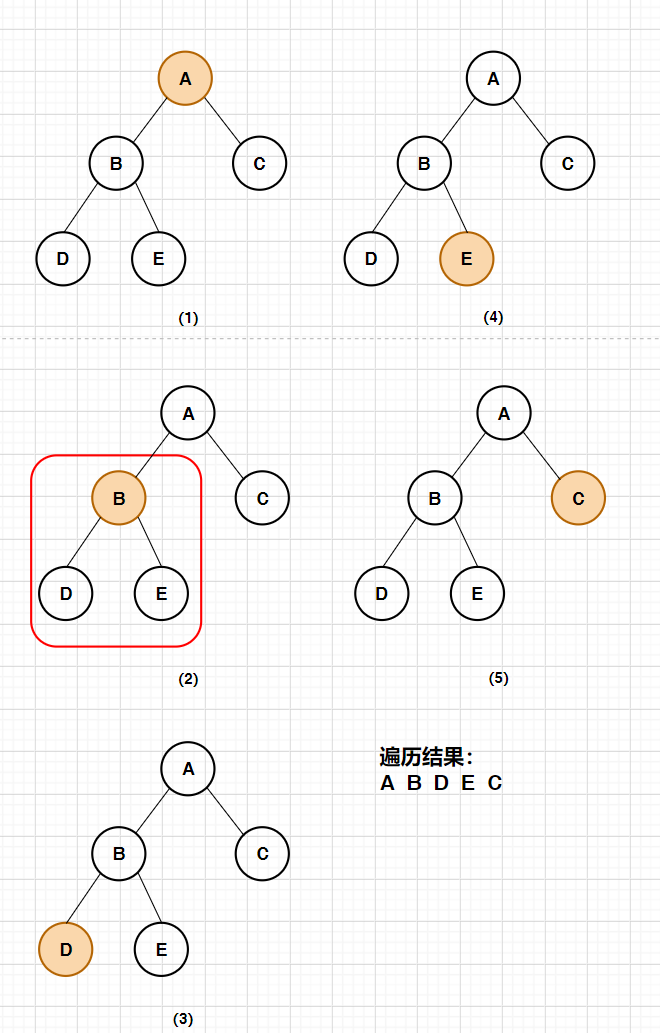
Code implementation:

public static void preOrder(Node root){
    //If it is an empty tree, return directly
    if(root == null){
        return;
    }
    //Access the root node first
    System.out.print(root.val+" ");
    
    //Recursive access to left subtree
    preOrder(root.left);
    //Recursive access to right subtree
    preOrder(root.right);
}

2. Middle order traversal

First recursively traverse the left subtree, access the root node, and then recursively traverse the right subtree (left root right)

Example:

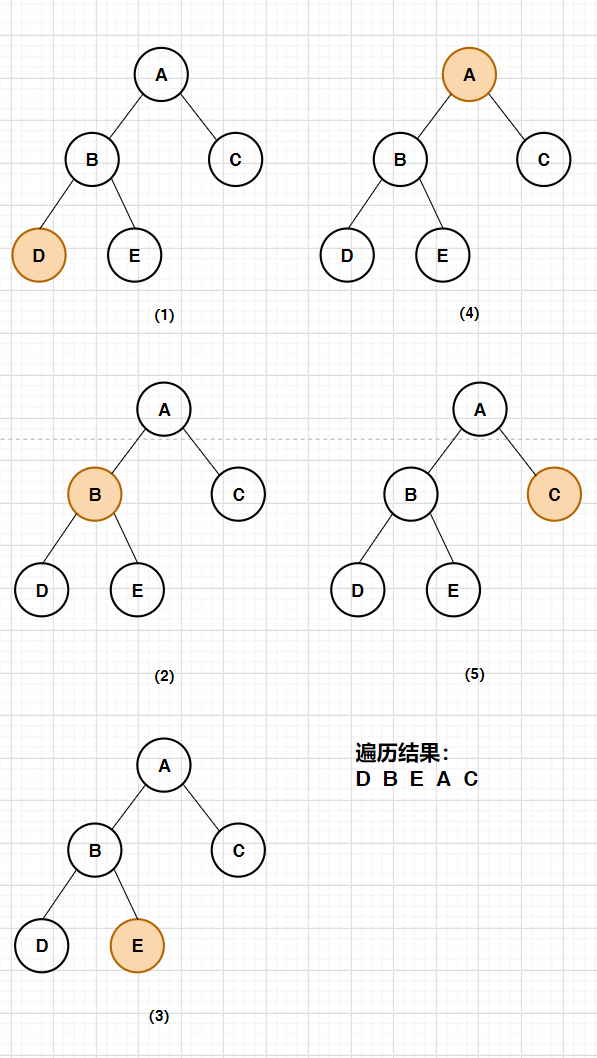
public static void inOrder(Node root){
    //If it is an empty tree, return directly
    if(root == null){
        return;
    }
    //Recursive access to left subtree
    inOrder(root.left);
    //Access root node
    System.out.print(root.val+" ");
    //Recursive access to right subtree
    inOrder(root.right);
}

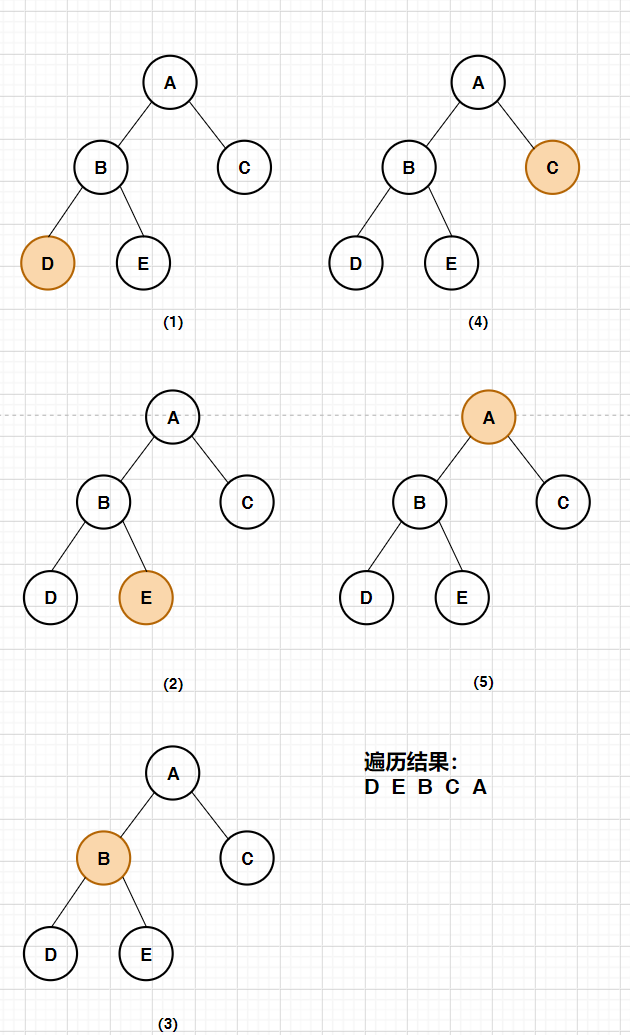
3. Post order traversal

First recursively traverse the left subtree, then recursively traverse the right subtree, and finally access the root node (left and right root)

Example:

public static void postOrder(Node root){
    //If it is an empty tree, return directly
    if(root == null){
        return;
    }
    //Recursive access to left subtree
    postOrder(root.left);
    //Recursive access to right subtree
    postOrder(root.right);

    //Access root node
    System.out.print(root.val+" ");
}

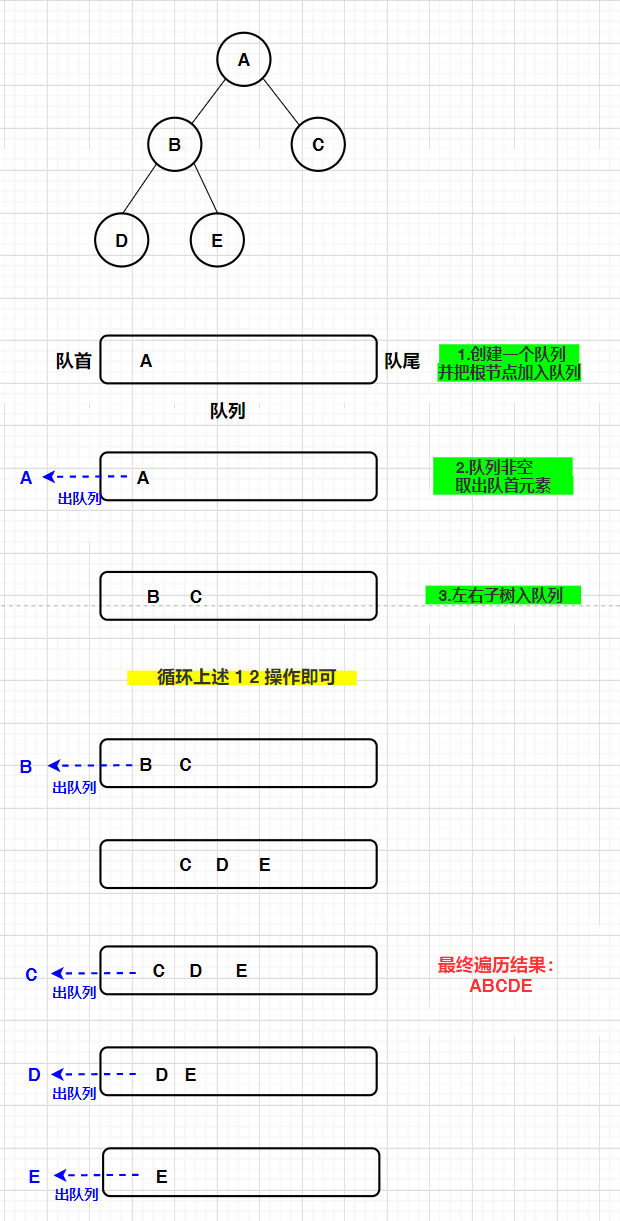
4. Sequence traversal

Traversal from layer to layer. Each layer is accessed from left to right. It is a non recursive operation

public static void levelOrder(Node root){
    //Create an empty queue and add the root node to the queue
    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);
    while( !queue.isEmpty()){
        //If the queue is not empty, take out the first element of the queue
        Node cur = queue.poll();
        //Access element
        System.out.print(cur.val + " ");

        //Queue the left and right subtrees
        if(cur.left != null){
            queue.offer(cur.left);
        }
        if(cur.right != null){
            queue.offer(cur.right);
        }
    }
}

Example:

Traversal Law:

• First traversal, the first visited node must be the root node
• In subsequent traversal, the last visited node must be the root node
• For middle order traversal and post order traversal, the first visited node is the leftmost node of the tree
• For first / second order traversal, the traversal results of subtrees are nested in the whole traversal results
• For medium order traversal, the traversal result of the left subtree is on the left side of the root node, and the traversal result of the right subtree is on the right side of the root node

Output results:

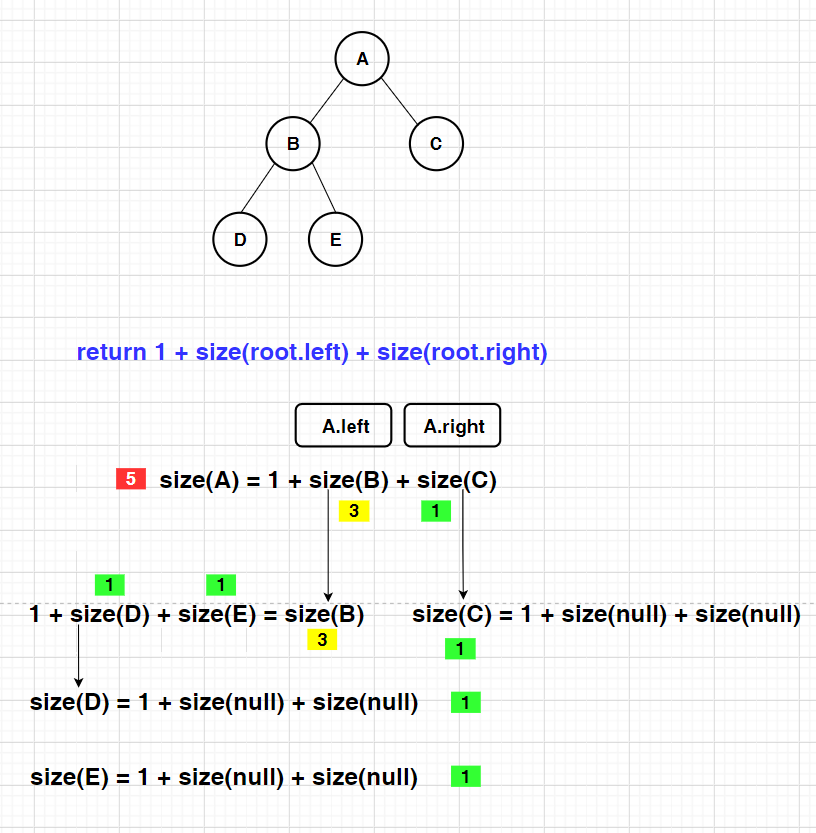
Find the number of binary tree nodes

public static int size(Node root){
    if(root == null){
        return 0;
    }
    //Total number of tree nodes = number of root nodes (1) + number of left subtree nodes + number of right subtree nodes
    return 1 + size(root.left) + size(root.right);
}

Output result: 5

Drawing analysis:

Execution sequence is as like as two peas.

Find the number of leaf nodes of binary tree

Leaf node: a node with a degree of 0

public static int leafSize(Node root){
    //Empty tree
    if(root == null){
        return 0;
    }
    //When there is only a root node, the root node is the only leaf node
    if(root.left == null && root.right == null){
        return 1;
    }
    // Number of root leaf nodes = number of root.left leaf nodes + number of root.right leaf nodes
    return leafSize(root.left) + leafSize(root.right);
}

Output result: 3

Drawing analysis:

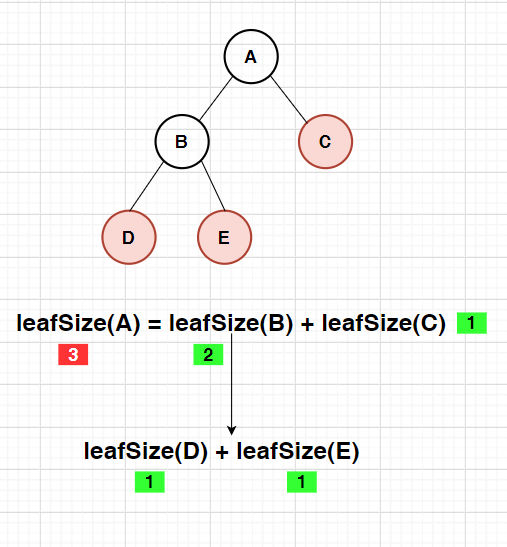
Find the number of nodes in layer K

public static int kLevelSize(Node root,int k){
    //If K < 1 or root is empty, it is an empty tree
    if(k < 1 || root == null){
        return 0;
    }
    //If k=1, it is the root node
    if(k == 1){
        return 1;
    }
    // Number of k-layer nodes = number of (k-1) layer nodes of the left subtree + number of (k-1) layer nodes of the right subtree
    return kLevelSize(root.left,k-1) + kLevelSize(root.right,k-1);
}

Output result: 2

Drawing analysis:

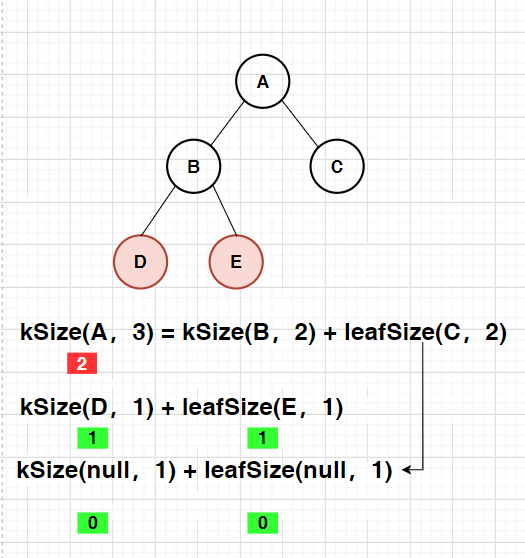
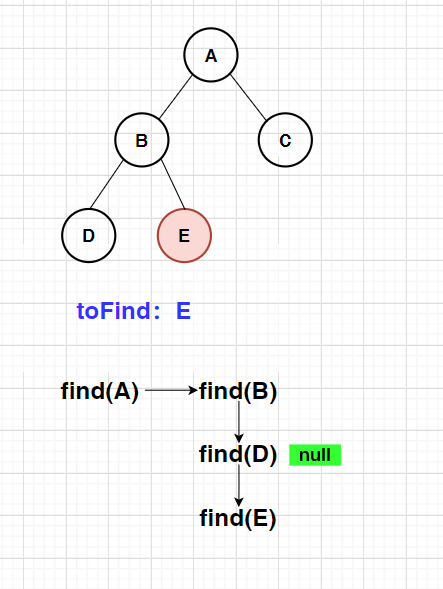
Finds the specified element in the binary tree

public static Node find(Node root,char toFind){
    if(root == null){
        return null;
    }
    if(root.val == toFind){
        return root;
    }
    //Recursive search for left and right subtrees
    Node result = find(root.left,toFind);
    if(result != null){
        return result;
    }
    return find(root.right,toFind);
}

Drawing analysis:

The next part will discuss the related interview questions of binary tree~~