Summary of data structure binary tree traversal ⭐⭐⭐
The concept of binary trees
1. The feature is that each node has at most two subtrees, left subtree and right subtree.
2. Full Binary Tree: i<=n/2 Round down, I is preceded by non-leaf nodes, I is followed by leaf nodes
(1) If n is odd, every non-leaf node has left and right children, because there is only one root node and n-1 is even, then the rest of the layers are multiples of 2
(2) If n is even, all non-leaf nodes except i=n/2_have left and right children
(3) Manchu binary tree is a special complete binary tree.
(4) A full binary tree with a height of h can be obtained by using the sum formula of equal-ratio columns with 2 h-1 nodes.
Extensions:
(1) The number of nodes with the most m-forks at h: N=(m h-1)/(m-1)
(2) m-forks with a height of H have at least h nodes (each node has only one child)
(3) Trees with a height of H and a degree of m have at least h+m-1 nodes. Build a tree with a height of h, at least h nodes, one node at each level, and then add M-1 nodes at any one node to build it
(4) Important formulas for non-empty binary trees: N0=N2+1
How do I use the properties of a full binary tree + the pre ordinal sequence, and the post ordinal sequence?
3. Complete Binary Tree
ergodic
Storage: Order?/ Chain? Define its data structure type?
Sequential storage:
typedef struct SeqTree{
int T[MaxSize];//Capacity and its size
int length;//length
}SeqTree
Chained storage:
typedef struct BTNode{
int data;//Data Domain
struct BTNode *lchild;//left child
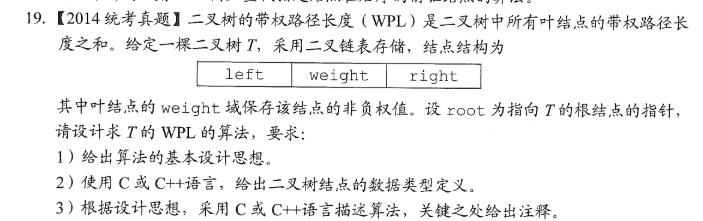
int weight;//Weight, WPL Kingdom P142 T19 True Question for 2014 Unified Examination
struct BTNode *rchild;//Right Child
}
Exercise Analysis and Code
1, P120 T7

Number of nodes equals the sum of degrees+1
The principle is that the direction of each branch of a non-leaf node is a node, and the branch tree of each node is the degree (outgoing) of that node, so adding the degrees of all nodes together is the number of all branches, but don't forget that the root node is not counted, only the outgoing (branch) of the root node is counted, so the number of nodes = the number of nodes equals the sum of degrees + 1
20x4+10x3+1x2+10x1+1=123
n4+n3+n2+n1+n0=123 so n0=82
Correct answer: B
2,P126 T4

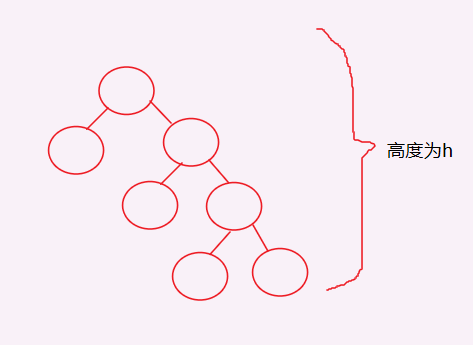
Because there are only nodes with degrees 0 and 2, in order to be as few as possible, only two nodes per layer except the root node can have a height of h, and all nodes have at least 2*h-1 nodes
The most special solution:
Complete binary tree is also a binary tree. It satisfies the nature. There are 2n nodes. In a complete binary tree, only one node has degree 1, that is, it can only be odd, so C is wrong.
A:n0=n n2=n-1 n0=1 n0+n2+n1=n A√
B:n0=2m n2=2m-1 n1=1 n0+n1+n2=4m, when 4m=n satisfies the condition B_
D:n2=2m n0=2m+1 n1=1 n0+n1+n2=4m+2=n, when m=(n-2)/4 meets the criteria D_


4,P126 T16

124 is an even number of complete binary trees in this question, n1=1
n0=n2+1 n2=123
sum=123+124+1=248
5,P126 T11

Layer 6 has eight leaf nodes, and layer 6 has 25-8=24 non-leaf nodes
So there are 24*2=48 leaf nodes in the 7th layer
Because it is a complete binary tree, the first six layers are 26-1=63
63+48=111
So if you change the subject, change the maximum to the minimum?
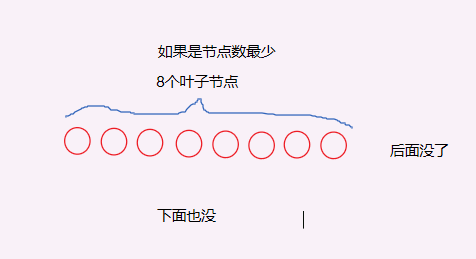
This results in eight leaf nodes with the fewest number of nodes.
Layer 6 8 Leaf Nodes
The first five layers are 25-1=31
So 31+8=39
Summarize the law:
1. A complete binary tree If the title already states how many leaf nodes are in one layer, the leaf nodes in the other layer will also be determined.
(2) To get the minimum number of nodes, and the title has already explained how many leaf nodes there are in a layer, the leaf nodes in that layer are placed first
(3) To get the maximum number of nodes, and the title has explained how many leaf nodes there are in a layer, then the leaf nodes in that layer are placed behind, so that there are also leaf nodes in the next layer, and the leaf node tree in the next layer = (Maximum number of nodes available in this layer - Leaf node tree in this layer)*2
Note that with leaf nodes that do not say the node of this layer, only how many leaf nodes are given in total. Ask questions that have multiple nodes to distinguish the type, such as T16 and T11, so summarize them together.

As you can see from the graph, when there is a degree 1 node on the previous layer, the leaf node tree of a complete binary tree does not change, which results in one more node than in the first case.
(1) When the first case occurs, all nodes except the last one are nodes with degree 2, then there are odd number of nodes, because the root node is designed
(2) When the second situation occurs: except that there is more than one node on the far right of the last layer, which happens to be added to the root node = 2, then the total number of nodes is even when added to other non-leaf nodes (degrees are 2).
This leads to
1 N1=1 when the total number of nodes is even
(2) N1=0 when the total number of nodes is odd

First understand the binary tree without right children node corresponding to the tree in the title: meaning, there is no right brothers in the corresponding tree
Fa 1: In extreme cases, the leaf nodes are all on the last level, so the last leaf node on the last level has no right brothers. The 1895 nodes above have only children and no brothers, totaling 1895+1=1896

Fa 2: By the nature of the binary tree, 116 leaf nodes, N2=N0-1=116-1=115 nodes with 2 degrees, only left or left children have no nodes, 2011-115=1896 nodes

A non-empty complete binary tree, where the leaf nodes are all on the same level and the non-leaf nodes have two children, is the nature of a full binary tree
K leaf nodes So non-leaf nodes are K-1, totaling 2K-1

In fact, there are pits here. A binary tree with 10 nodes may only need 16 storage units if it satisfies a height of 5. However, the node on the fifth layer can only be placed at the top, but it does not satisfy the arbitrariness of the height of the binary tree being 5. In fact, the 10 nodes are used to pit people. The key information or height is 5. At least 25-1=31 nodes are required to convert binary trees into sequential storage
So why are the 10 nodes pit people? Because if the fifth level of the binary tree of the 10 nodes has one node on the far right, that is, node 31, then the binary tree with arbitrary height of 5 will not be converted to a sequentially stored binary tree if 16 of the least used cases are used.
Traversal of Binary Trees and Threaded Binary Trees
Preorder traversal
Recursive sequential traversal
Priority Traversal Order: Root around
void PreOrder(BiTree T){
if(T){//Non-empty condition
visit(T);//Visit
PreOrder(T->lchild);//left child
PreOrder(T->lchild);//Right Child
}
}
non-recursive algorithm
void PreOrder(BiTree T){
Stack S;//Stack
InitStack(S);//Initialization of stack
BiTree p;//Auxiliary Pointer
while(IsEmpty(S)||p!=NULL){
if(p){//Non-empty
visit(p);//Visit
Push(S,p);//Stack
p=p->lchild;//Continue to visit their left child until a null pointer appears
}
else{//Empty, put their parent nodes out of the stack
Pop(S,p);//The top element of the stack goes out of the stack and into the p-pointer
p=p->rchild;//Visit Right Child
}
}
}
Intermediate traversal
Recursive Ordered Traversal
Medium traversal order: Left Root Right
void InOrder(BiTree T){
if(T){//Non-empty condition
PreOrder(T->lchild);//left child
visit(T);//Visit
PreOrder(T->lchild);//Right Child
}
}
non-recursive algorithm
void InOrder(BiTree T){
Stack S;//Stack
InitStack(S);//Initialization of stack
BiTree p;//Auxiliary Pointer
while(IsEmpty(S)||p!=NULL){
if(p){//Non-empty
Push(S,p);//Stack
p=p->lchild;//Continue to visit their left child until a null pointer appears
}
else{//Empty, put their parent nodes out of the stack
Pop(S,p);//The top element of the stack goes out of the stack and into the p-pointer
visit(p);//Visit
p=p->rchild;//Visit Right Child
}
}
}
Post-order traversal ⭐
recursive algorithm
Post-order traversal order: Left and right roots
void PostOrder(BiTree T){
if(T){//Non-empty condition
PreOrder(T->lchild);//left child
PreOrder(T->lchild);//Right Child
visit(p);//Visit
}
}
Non-recursive post-order traversal algorithm ⭐⭐ (Frequent after-school questions)
typedef struct Stack{
BiTree t;//Binary Tree Pointer
int tag;//Tag, tag=0 accesses left subtree, tag=1 accesses right subtree
}
int top;//top of stack
void PostOrder(BiTree T){
Stack S[MaxSize];//Stack, MaxSize large enough
top=0;
while(T||top>0){//Node exists or stack is not empty
while(T){//Loop until left child is empty
S[++top].t=T;//Push
S[top].tag=0;//Access left node
T=T->lchild;//Access left node
}
while(S[top].tag==1&&top>0){
visit(S[top].t);//Visit
top--;//The node is out of stack after it has been visited!
}
if(top>0){//top remains > 0 after the last while loop ends
//Explain that the right child with nodes is not visited
//Only when the left and right children have visited, can they visit their parents'nodes
S[top].tag=1;
T=S[top].t->rchild;//Traverse their right child
}
}
}
Comparison of non-recursive and recursive postorder Traversals
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 10000
typedef struct BTnode{
int data;
struct BTnode *lchild;//left child
struct BTnode *rchild;//Right Child
}BTnode,*BiTree;
typedef struct Stack{
BiTree t;//Binary Tree Pointer
int tag;//Tag, tag=0 accesses left subtree, tag=1 accesses right subtree
}Stack;
int top;//top of stack
void visit(BiTree t){
printf("%d ",t->data);
}
void PostOrder1(BiTree T){
if(T){
PostOrder1(T->lchild);
PostOrder1(T->rchild);
visit(T);
}
}
void PostOrder(BiTree T){
Stack S[MaxSize];//Stack, MaxSize large enough
top=0;
while(T||top>0){//Node exists or stack is not empty
while(T){//Loop until left child is empty
S[++top].t=T;//Push
S[top].tag=0;//Access left node
T=T->lchild;//Access left node
}
while(S[top].tag==1&&top>0){
visit(S[top].t);//Visit
top--;//The node is out of stack after it has been visited!
}
if(top>0){//top remains > 0 after the last while loop ends
//Explain that the right child with nodes is not visited
//Only when the left and right children have visited, can they visit their parents'nodes
S[top].tag=1;
T=S[top].t->rchild;//Traverse their right child
}
}
}
int main(){
BiTree T7=(BiTree)malloc(sizeof(BTnode));
T7->data=7;
BiTree T3=(BiTree)malloc(sizeof(BTnode));
T3->data=3;
T7->lchild=T3;
BiTree T6=(BiTree)malloc(sizeof(BTnode));
T6->data=6;
T7->rchild=T6;
BiTree T1=(BiTree)malloc(sizeof(BTnode));
T1->data=1;
T3->lchild=T1;
T1->lchild=NULL;
T1->rchild=NULL;
BiTree T2=(BiTree)malloc(sizeof(BTnode));
T2->data=2;
T3->rchild=T2;
T2->lchild=NULL;
T2->rchild=NULL;
BiTree T4=(BiTree)malloc(sizeof(BTnode));
T4->data=4;
T6->lchild=T4;
T4->lchild=NULL;
T4->rchild=NULL;
BiTree T5=(BiTree)malloc(sizeof(BTnode));
T5->data=5;
T6->rchild=T5;
T5->lchild=NULL;
T5->rchild=NULL;
printf("Recursive postorder traversal algorithm:");
PostOrder1(T7);
printf("\n");
printf("Non-recursive post-order traversal algorithm:");
PostOrder(T7);
}
5.3.3 Exercise Analysis and Summary
Choice question
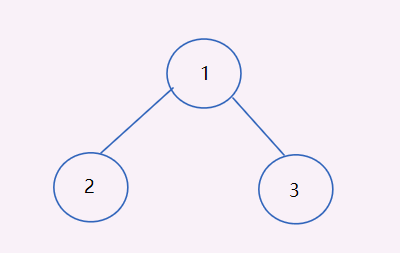
1,P138 T1

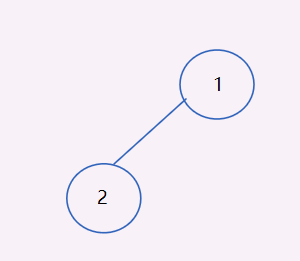
In this diagram:
The median traversal is: 2 1
The order traversal is: 1 2
A, B exclude first
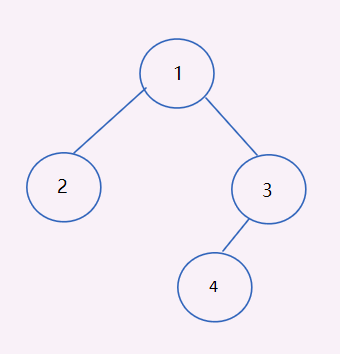
The sequence is: 1 2 3 4
The middle order is: 2 1 4 3 D does not satisfy D error
If a leaf node is the last node that is traversed in middle order, indicating that the node is on the right-most side of the graph and that there are no left and right children, then the rightmost side of the graph must be reached when traversing in order, so the node with no left or right children is the last node, so they both stop at the same node
2,P139 T9
Order: around root
Postorder: left and right roots
There are two cases in which the sequence is reversed:
1. Each node has only a right child
(2) Each node has only a left child
Then each node degree 1 will have only one leaf node
So the correct answer is C

Order: around root
Middle order: left root right
To have the same sequence:
1. Each node has only a right child - > only a right subtree
The correct answer is B
However, some people may choose C, but C can only guarantee a degree of 1, it may only have left children, it may only have right children, it can not guarantee only left children, this is a necessary and sufficient condition

If left and right subtrees are not empty in the sequence of precedence, then the last node at the end must be the right domain, because the last leaf node has only one precursor, and then there is no more than NULL
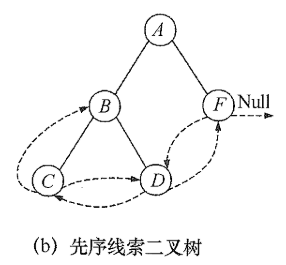
The left subtree is empty
Threaded Binary Tree Test Selection Question, just iterate through it until you can connect the dotted lines
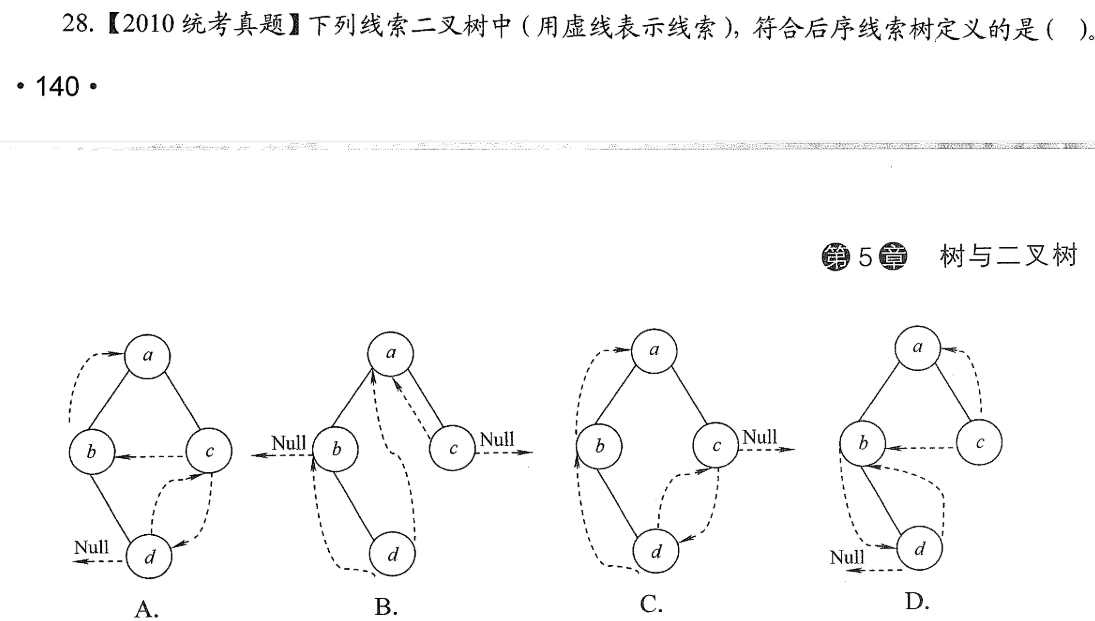
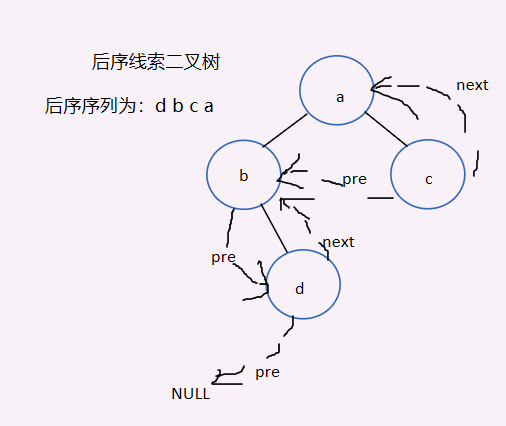
Infer other things from one fact

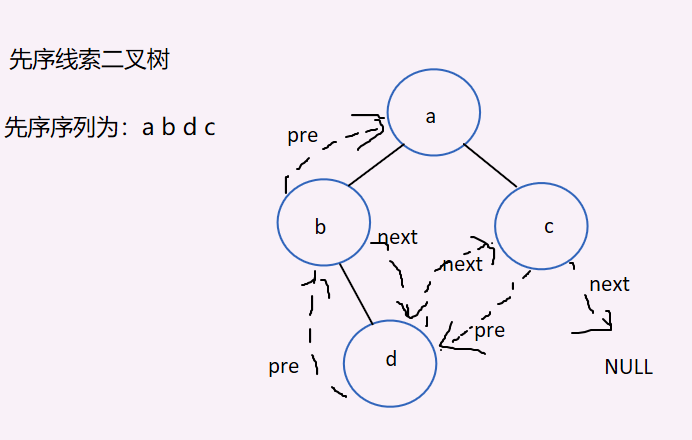
Summary:
Draw a threaded binary tree by first writing out the corresponding traversal order (for clarifying ideas and validating lines)
Depending on the traversal process, a left or right subtree is threaded when it is empty. Start at one node of the output.

Order: around root
Postorder: left and right roots
1. Each node has only a right child
(2) Each node has only a left child
Summarize as follows:
1 Or degree 1
(2) Height equals number of nodes
Answer Choose B
Comprehensive Topic
1,P141 T3

Method 1: Change the middle traversal + read stack without stacking
void PostOrder(BiTree T){
Stack S;//Definition stack to hold binary tree nodes
InitStack(S);//Stack Initialization
BiTree p=NULL;//Used to determine if a node has recently passed the stack
while(T||!IsEmpty(S)){//Node is not empty/Stack is not empty
if(T){//Node is not empty
Push(T);//Node stacking
T=T->lchild;//Go left until empty
}
else{//The leftmost end is the end
GetTop(S,T);//Read top element
if(T->rchild&&T->rchild!=p){
//Node's right subtree exists and has not been visited
T=T->rchild;//Go to the right child
}
else{//The left subtree is gone, the right subtree does not exist or has been visited
//That is, access the node
Pop(S,T);//Top element out of stack
visit(T);//Access this node
p=T;//Update the currently recently visited node to prevent parent nodes from judging that the right child is not empty causing a dead cycle
T=NULL;//Clears the contents of the T pointer because the left and right subtrees of the pointer, including its nodes, have been accessed out of the stack
}
}
}
}
Method 2: Customize the data structure of the stack, including tag tag tag, tag=0 visited the left child, tag=1 had children, tag=1 only accessed when both left and right children visited and there were elements in the stack.
typdef struct Stack{
BiTree t;//Binary Tree Pointer
int tag;//tag=0 visits left child; tag=1 Visit right child
}Stack;
int top;//top of stack
void PostOrder(BiTree T){
Stack S[MaxSize];//MaxSize is large enough
top=0;//top of stack
while(T||top>0){//Node is not empty or stack is not empty
while(T){//Non-empty goes all the way to the left
S[++top]=T;//Push
S[top].tag=0;//Visit Left Node Children
T=T->lchild;//Go to the left child
}
while(S[top].tag==1&&top>0){//Their child nodes are visited and there are children on the stack
visit(S[top].t);//Access this node
top--;//Stack Out
}
if(top>0){//top hasn't reached 0 yet after the while loop above, and there are elements in the stack
//Note that the right child with nodes has not been visited yet
S[top].tag=1;//This node records travels
T=S[top].t->rchild;//Go to their right child to continue visiting
}
}
}
F3: Order (reverse left-right order + stack output)
void PostOrder2(BiTree T){//F3: Order (reverse left-right order + stack output)
if(!T)
return;
BiTree S[MaxSize];//Large enough for traversal
BiTree S1[MaxSize];//Stack for Output
int top=-1,top1=-1;//top of stack
while(T||top>-1){
while(T){
S[++top]=T;//Push
S1[++top1]=T;//Push
T=T->rchild;//Go to right child, reverse order, go right first
}
if(top>-1){//There are still nodes in the stack
T=S[top--];//Gettop
T=T->lchild;//Go to the left child
}
}
//printf("%d %d\n",top1,top);
while(top1!=-1){//output
visit(S1[top1--]);//Visit
}
}

This is a non-recursive algorithm. First, a recursive algorithm is introduced to find the height of a binary tree.
int high(BiTree T,int h){//Binary Tree Pointer and Record Current Height
int lh,rh,max;//Left and right subtree height
if(T){
lh=high(T->lchild,h+1);//Recursive Left Subtree
rh=high(T->rchild,h+1);//Recursive Right Subtree
return ((lh>rh)?lh:rh)+1;
}
}
Non-recursive algorithm for binary tree height calculation
1. Sequence traversal
int high(BiTree T){
if(!T)//Empty Tree Return
return -1;
int front=-1,rear=-1;//Head and tail pointer
int last=0;//Pointer to the last node of the layer
int level=0;//height
BiTree Q[MaxSize];//queue
Q[++rear]=T;//Root node enqueued
BiTree p;//Auxiliary pointers are used to save queue nodes
while(front<rear){//Queue head pointer is smaller than queue end pointer, proving there are elements
p=Q[++front];//Queue Head Node Out
if(p->lchild)//Left Child Exists
Q[++rear]=p->lchild;//Left Child Entering the Team
if(p->rchild)//Right Child Exists
Q[++rear]=p->rchild;//Right Child Entering Team
if(last==front){//The queue head pointer has reached the last node of the layer
last=rear;//Update End Pointer of Next Layer
level++;//Height Self-Increasing
}
}
return level;//Return Height
}
What if I change this question to find the width of a binary tree?
The simple way is to add a record of the maximum number of nodes in each layer to the non-recursive hierarchical traversal of the previous question
int width(BiTree T){//Find Width
if(!T)//Empty Tree Return
return -1;
int front=-1,rear=-1;//Head and tail pointer
int last=0;//Pointer to the last node of the layer
int count=0;//Record the number of nodes per layer
int max=0;//Save maximum width
BiTree Q[MaxSize];//queue
Q[++rear]=T;//Root node enqueued
BiTree p;//Auxiliary pointers are used to save queue nodes
while(front<rear){//Queue head pointer is smaller than queue end pointer, proving there are elements
p=Q[++front];//Queue Head Node Out
count++;//Number of nodes in this layer increases by itself
if(p->lchild)//Left Child Exists
Q[++rear]=p->lchild;//Left Child Entering the Team
if(p->rchild)//Right Child Exists
Q[++rear]=p->rchild;//Right Child Entering Team
if(last==front){//The queue head pointer has reached the last node of the layer
last=rear;//Update End Pointer of Next Layer
max=(max>count)?max:count;
count=0;//At the end of each layer, count 0
}
}
return max;//Return maximum width
}

//Using Recursive Algorithms to Build Binary Trees
BiTree create(ElemType *xian,ElemType *zhong,int len){
int i;//A pointer to find left and right subtrees by traversing an ordered sequence
if(len==0)
return NULL;//Empty Tree
BiTree temp=(BiTree)malloc(sizeof(BTnode));//Create Pointer
temp->data=*xian;//Value assignment
for(int i=0;i<len;i++){
if(*(zhong+i)==*xian)//Brea if both values are equal, record this location for recursion
break;
}
temp->lchild=create(xian+1,zhong,i);//Recursive Left Subtree
temp->rchild=create(xian+i+1,zhong+i+1,len-i-1);//Recursive Right Subtree
return temp;
}


Queue to determine if a binary tree is a complete binary tree
bool IsComTree(BiTree T){//Determine whether it is a complete binary tree
if(!T)
return false;//Empty Tree
BiTree Q[MaxSize];//Large enough capacity
int front=-1,rear=-1;//Head and tail pointer
Q[++rear]=T;//Root Node Entry
BiTree p;//Auxiliary pointers are used to save queued nodes
while(front<rear){//Queue head pointer is less than queue end pointer
p=Q[++front];//Queue Head Node Out
if(p){//Non-NULL Nodes
//Team up both left and right children
Q[++front]=p->lchild;
Q[++front]=p->rchild;
}
else{//If you encounter a leaf node, then you cannot have any more nodes behind you, otherwise it is not a complete binary tree
while(front<rear){//Retire in Cycle
p=Q[rear--];//Queue
if(p)//There are even non-empty nodes
return false;//Not a complete binary tree
}
}
}
return true;//Is a complete binary tree
}

Using non-recursive sequential traversal algorithm
int PreOrderFind(BiTree T,int k){
int top=-1;//top of stack
BiTree Stack[MaxSize];//MaxSize is large enough
int i=0;//For comparison with k
while(top>-1||T){//When there are nodes in the stack or currently accessed nodes are not empty
if(T){
i++;
if(i==k)//Reaching the k th element
return T->data;//Returns the value of its node
Stack[++top]=T;//Push
T=T->lchild;//Go straight to the left
}
else{//When an empty node is encountered, return to its parent node and go right
T=Stack[top--];//Top node out of stack
T=T->rchild;//Turn right
}
}
return -1;//No k th value found
}
Using recursive writing
int flag=0;//Marks if the kth node is found
int i=0;//number
void PreOrderFind1(BiTree T,int k){//Priority Sequence Recursive Algorithm Finds the Value of the k th Node
if(T){//Non-empty condition
i++;//Self-Increasing ith Node
if(i==k){
visit(T);
flag=1;
return;
}
if(flag!=1){
PreOrderFind1(T->lchild,k);//left child
PreOrderFind1(T->rchild,k);//Right Child
}
else
return;
}
}

Using recursive algorithm
int flag=0;
void PostOrder(BiTree T,int x){
if(!T)//Empty Tree
return;
if(T->data==x){//Find nodes with x values
flag=1;//sign
return;//Return
}
if(flag==0){
PostOrder(T->lchild,x);//Recursive Left Subtree
}
if(flag==0){
PostOrder(T->lchild,x);//Recursive Left Subtree
}
if(flag!=0){//x found
visit(T);
}
}
Use non-recursive post-order traversal algorithm to find --------- custom stack algorithm - Tags
typedef Stack{
BiTree t;//Pointer field
int tag;//tag=0 accesses left node, tag=1, right node
}Stack;
void PostOrderFindX1(BiTree T,int x){
//Find all the ancestors of x--Custom stack algorithm--Tags
if(!T)//Empty Tree
return;
Stack S[MaxSize];//Stack, large enough
int top=-1;//Top of Stack
while(top>-1||T){//Tree is not empty or has nodes in stack
while(T){//Keep going to the left when not empty
S[++top].t=T;//Push
S[top].tag=0;//Right Node Visited
T=T->lchild;//Turn left
}
if(S[top].t->data==x){
for(int i=top-1;i>=0;i--)
visit(S[i].t);
break;
}
//Exiting while means an empty node was encountered
while(S[top].tag==1&&top>-1){
top--;//Unstack once visited
}
if(top>-1){//top also >-1 through the upper while loop
//Right child with node not visited
S[top].tag=1;//Mark this node
T=S[top].t->rchild;//Visit Right Child
}
}
}
Use non-recursive post-order traversal algorithm to find - - order (reverse order) + stack output (problematic)
void PostOrderFindAn(BiTree T,int x){
int top=-1,top1=-1;//Dual stack writing, one stack for traversal and one stack for output
BiTree S[MaxSize];//Traverse Stack
BiTree S1[MaxSize];//Output stack
while(top>-1||T){//There are nodes in the stack, or the tree is not empty
while(T){
S[++top]=T;//Push
S1[++top1]=T;//Push
T=T->rchild;//Go right first
//Because the right node is accessed more slowly than the left node in post-order traversal, the subtree root node is accessed more slowly than the right node
//Left-, Right-, Root
//Depending on the nature of the stack, the stack-first access occurs later
//Therefore, after the subtree root node is on the stack, walk the right child first and let the right child on the stack
}
if(S1[top1]->data==x){//Location of x found
for(int i=top-1;i>=0;i--)
visit(S1[i]);
exit(1);
}
if(top>-1){//There are also nodes in the stack
T=S[top--];//Remove top node from stack
T->lchild;//Visit left child
}
}
}

typedef Stack{
BiTree t;//Pointer field
int tag;//tag=0 accesses left node, tag=1, right node
}Stack;
//ROOT Root Node p q Any two nodes
//ROOT Root Node p q Any two nodes
BiTree ANCESTOR(BiTree ROOT,BiTree p,BiTree q){//Post-order non-recursive computation common ancestor
Stack S[MaxSize];//Stack, large enough
Stack S1[MaxSize];//Stack, large enough to hold the contrast pointer
int top=-1;//top of stack
int top1=-1;//Top of stack of comparison stack
BiTree T=ROOT;//Auxiliary Pointer
while(T||top>-1){
while(T){//If Node Exists
S[++top].t=T;//Push
S[top].tag=0;//Record Access Left Subtree
T=T->lchild;//Turn left
}
while(top>-1&&S[top].tag==1){//Both left and right subtrees have been visited
if(p==S[top].t){//Location of p found
for(int i=0;i<=top;i++)
S1[i].t=S[i].t;//Transfer corresponding data to another stack for comparison
top1=top;//Top of Assignment Stack
}
if(q==S[top].t){//Find the location of q and start comparing
for(int i = top;i>=0;i--){//Look backwards from top because you want to find the closest public node
for(int j=top1;j>=0;j--){
if(S[i].t==S1[j].t)//If there is a public node, it returns
return S[i].t;//Return Pointer
}
}
}
top--;//Stack Out
}
if(top>-1){//After the while loop above, when top returns >-1, the right child of another node is not visited
S[top].tag=1;//Mark Access to Right Child
T=S[top].t->rchild;//Remove top stack element
}
}
return NULL;
}
There's a question: What's the difference between this if(pS[top].t) and this if(qS[top].t) inside and outside of while?
BiTree ANCESTOR1(BiTree ROOT,BiTree p,BiTree q){//Post-order non-recursive computation common ancestor
Stack S[MaxSize];//Stack, large enough
Stack S1[MaxSize];//Stack, large enough to hold the contrast pointer
int top=-1;//top of stack
int top1=-1;//Top of stack of comparison stack
BiTree T=ROOT;//Auxiliary Pointer
while(T||top>-1){
if(p==S[top].t){//Location of p found
for(int i=0;i<=top;i++)
S1[i].t=S[i].t;//Transfer corresponding data to another stack for comparison
top1=top;//Top of Assignment Stack
}
if(q==S[top].t){//Find the location of q and start comparing
for(int i = top;i>=0;i--){
for(int j=top1;j>=0;j--){
if(S[i].t==S1[j].t)//If there is a public node, it returns
return S[i].t;//Return Pointer
}
}
}
while(T){//If Node Exists
S[++top].t=T;//Push
S[top].tag=0;//Record Access Left Subtree
T=T->lchild;//Turn left
}
while(top>-1&&S[top].tag==1){//Both left and right subtrees have been visited
top--;//Stack Out
}
if(top>-1){//After the while loop above, when top returns >-1, the right child of another node is not visited
S[top].tag=1;//Mark Access to Right Child
T=S[top].t->rchild;//Remove top stack element
}
}
return NULL;
}
The results of both operations are as follows
Tests on different data are the same
So what's the difference between the two?

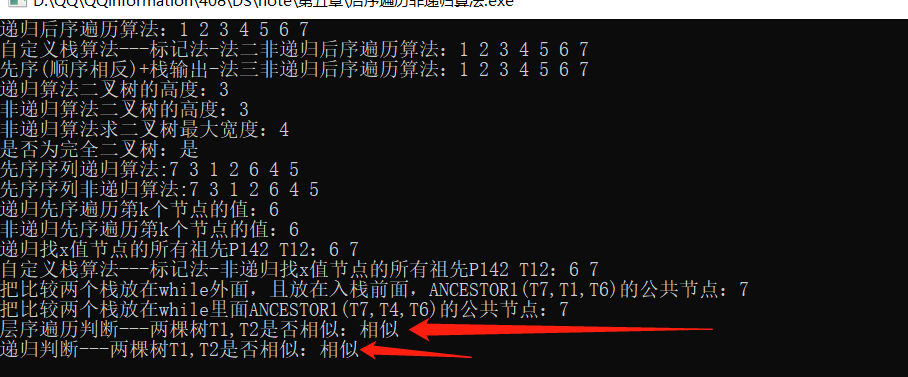
Method 1: (This is the method I used) Compare two trees in a hierarchical traversal. Only if the results of each traversal of the two trees are either empty nodes, left or right children, or left or right will they continue execution, otherwise false will be returned
bool LevelOrder(BiTree T1,BiTree T2){//Hierarchical traversal to identify whether two trees are similar
//Continue execution when neither tree is empty, or both trees are empty, otherwise return false, not similar
if(!((T1&&T2)||(T1==NULL&&T2==NULL)))
return false;
if(T1==NULL&&T2==NULL)//Both are null and return true directly similar
return true;
BiTree Q1[MaxSize];//Queue of Tree 1
int front1=-1,rear1=-1;//Tree 1 Queue Head and End Pointer
BiTree Q2[MaxSize];//Queue of Tree 2
int front2=-1,rear2=-1;//Tree 2 Queue Head and End Pointer
BiTree p1,p2;//Secondary pointer to save queued nodes
Q1[++rear1]=T1;//Tree 1 Root Node Enqueued
Q2[++rear2]=T2;//Tree 2 Root Node Enqueued
while(front1<rear&&front2<rear2){
p1=Q1[++front1];//Tree 1 Queue Head Out
p2=Q2[++front2];//Tree 1 Queue Head Out
if(p1->lchild&&p2->lchild){//Both left children
//Then all the left children join the team
Q1[++rear1]=p1->lchild;//The left child of Tree 1 joined the team
Q2[++rear2]=p2->lchild;//Tree 2 left child enrolled
}
//Both are empty with no processing and are similar by default
else if(T1->lchild||T2->lchild)//It is not the same as long as one of them has a left child
return false;
if(p1->rchild&&p2->rchild){//Both left children
//Then all the right children join the team
Q1[++rear1]=p1->rchild;//Tree 1's right child joins the team
Q2[++rear2]=p2->rchild;//Tree 2's Right Child Enrolled
}
//Both are empty with no processing and are similar by default
else if(T1->rchild||T2->rchild)//As long as one of them has a right child, they are not the same
return false;
}
return true;//It's all done. It's true before returning to flase
}
The results are as follows:

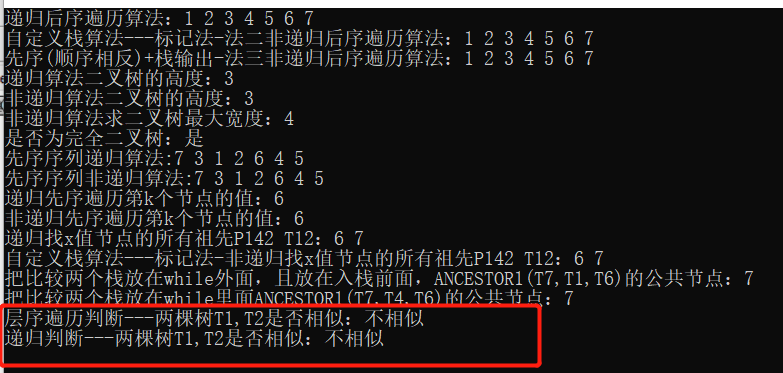
Method 2: Recursive algorithm
int Similar(BiTree T1,BiTree T2){
int LeftS,RightS;//Are left and right subtrees similar
if(T1==NULL&&T2==NULL)//Both trees are empty
return 1;
else if(T1==NULL||T2==NULL)//One of the two trees is empty
return 0;
else{//Both trees exist
LeftS=Similar(T1->lchild,T2->lchild);//Recursive Left Subtree
RightS=Similar(T1->rchild,T2->rchild);//Recursive Left Subtree
return LeftS&&RightS;//Similarity is when both sides are similar.
}
}
Compare results (two different types of data)
Examine the true questions, solve more than one question
What I'm using is hierarchical traversal
Idea: Through sequential traversal, record the total WPL with a variable sum, record the current depth/height, each time to determine if the node is a leaf node, if it is a leaf node, multiply its weight and depth into the sum, if not, continue sequential traversal.
int LevelOrderWPL(BiTree T){
if(!T)
return 0;//Empty Tree
int sum=0;//Record WPL totals
int front=-1,rear=-1;//Head and tail pointer
int last=0;//The pointer to the last node of the layer, and the root node is indexed by number 0, so last is initially zero
int level=0;//depth
BiTree Q[MaxSize];//queue
Q[++rear]=T;//Root node enqueued
BiTree p;//Auxiliary pointers are used to save queue nodes
while(front<rear){//Queue head pointer is less than queue end pointer, there are nodes
p=Q[++front];//Queue Head Node Out
if(p->lchild)//With a left child
Q[++rear]=p->lchild;//Left Child Enrolled
if(p->rchild)//Has Right Child
Q[++rear]=p->rchild;//Right Child Enrolled
if(p->lchild==NULL&&p->rchild==NULL)
sum+=(level)*p->weight;//accumulation
if(front==last){//Reach the last node of the layer
last=rear;//Update to the next level's tail pointer
level++;//Depth self-increasing
}
}
return sum;//Return to WPL
}
Fa 2 - - traversal in order
int WPL=0;//Global traversal of WPL variables
int PreOrderWPL(BiTree T,int h){//Current Depth
if(T->lchild==NULL&&T->rchild==NULL)//leaf node
WPL+=T->weight*h;//accumulation
if(T->lchild)
PreOrderWPL(T->lchild,h+1);//Recursive Left Child
if(T->rchild)
PreOrderWPL(T->rchild,h+1);//Recursive Right Child
return WPL;//Return Variable
}
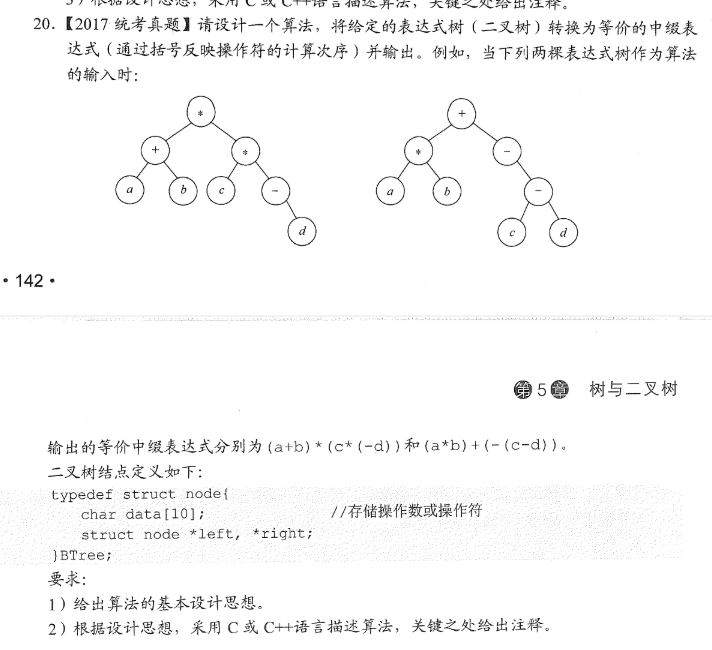
Method 1: When I write, I use the middle-order traversal recursive algorithm + global traversal to determine if parentheses should be added. If an operator is encountered for the first time, no parentheses are added. If it is not a leaf node and it is not the first time an operator is encountered, add () before visiting the left child and'(') after visiting the right child. If it is a leaf node, output the operands.
void InOrder(OpTree T){
if(!T)
return;//Empty returns
if(T->lchild==NULL&&T->rchild==NULL)//leaf node
printf("%c",T->data);
else{//Nonleaf Nodes
count++;
if(count!=1)//Not the first time you encounter an operator
printf("(");
if(T->lchild)
InOrder(T->lchild);//Recursive Left Subtree
printf("%c",T->data);
if(T->rchild)
InOrder(T->rchild);//Recursive Right Subtree
if(count!=1)
printf(")");
count--;
}
}
The results are as follows