Summarize the four traversal methods of binary tree, using recursion and iteration. The recursive code is relatively simple, and the iterative code is relatively complex.
1, Preorder traversal
(here, take the printed results as an example, you can also use ArrayList to store the val in the subtree)
thinking
Recursion: first the root node, then the left subtree, and then the right subtree.
Iteration: you need to use the stack. Press the stack root first and enter the cycle (the end cycle condition is that the stack is empty), then pop the stack and print val with top. If it is judged that the right subtree of top is not empty, press the stack. Judge that the left subtree of top is not empty and press the stack (the two judgment sequences cannot be changed). Take the picture and understand it intuitively.
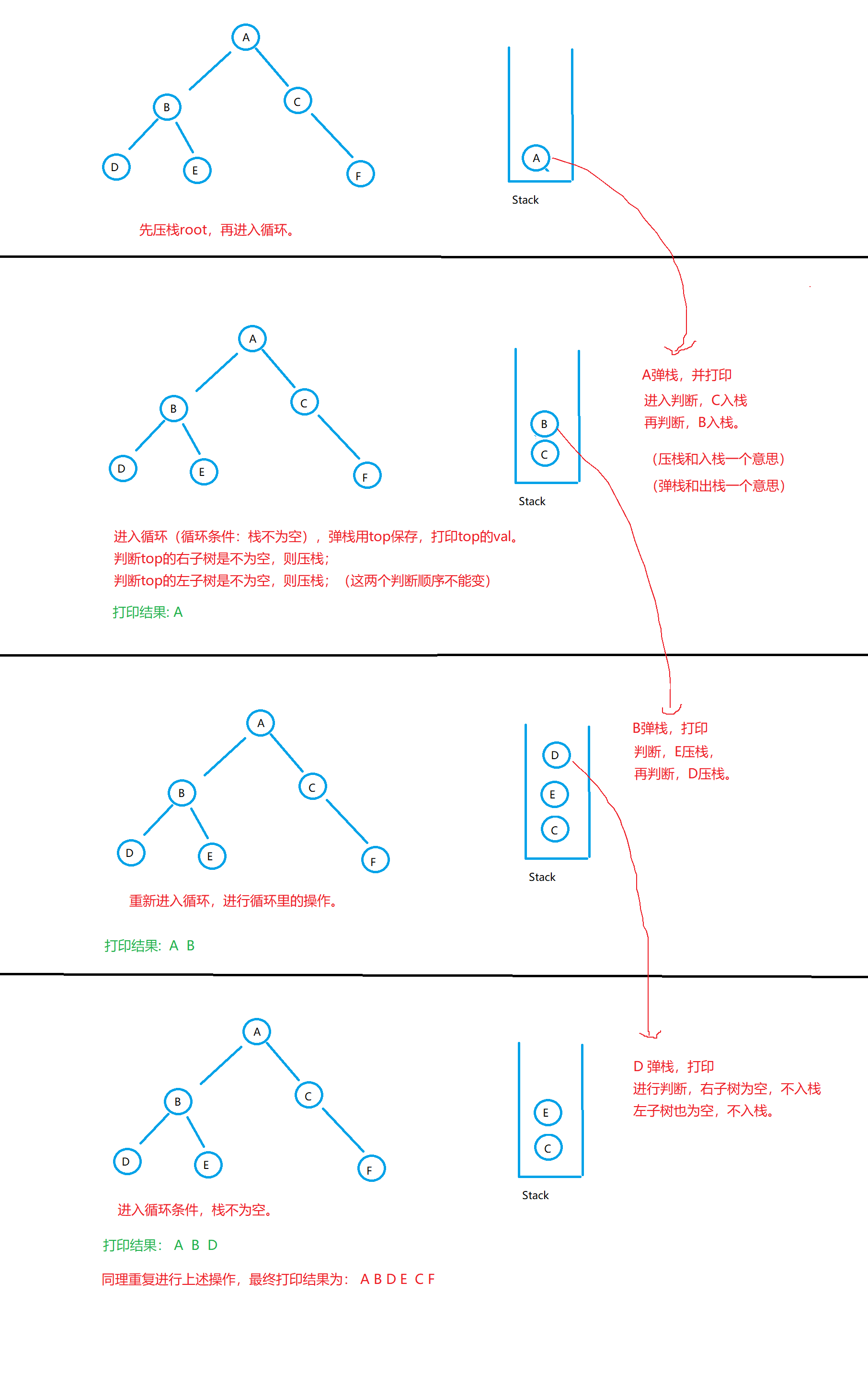
code
recursion
public static void preOrder(Node root){
//The root node is empty and ends directly
if(root==null){
return;
}
//Root node
System.out.print(root.val+" ");
//Left subtree
preOrder(root.left);
//Right subtree
preOrder(root.right);
}
iteration
public static void preOrder(TreeNode root){
//The root node is empty and ends directly
if(root==null){
return;
}
Stack<TreeNode> s=new Stack<>();
//First in stack
s.push(root);
while (!s.empty()){
TreeNode top=s.pop();
System.out.print(top.val+" ");
//From right to left, the order should not be disordered
if(top.right!=null){
s.push(top.right);
}
if(top.left!=null){
s.push(top.left);
}
}
}
2, Medium order traversal
thinking
Recursion: first root the left subtree, then the root node, and then the right subtree.
Iteration: cur=root, entering an endless loop (there are if judgment conditions in it. If the stack is empty, break);
1. Enter another cycle. If cur is not empty, it will be put on the stack until the left subtree is empty.
2. if the stack is empty, the loop will end.
3. Play stack and print.
4.cur=top.right.
Repeat the above operation
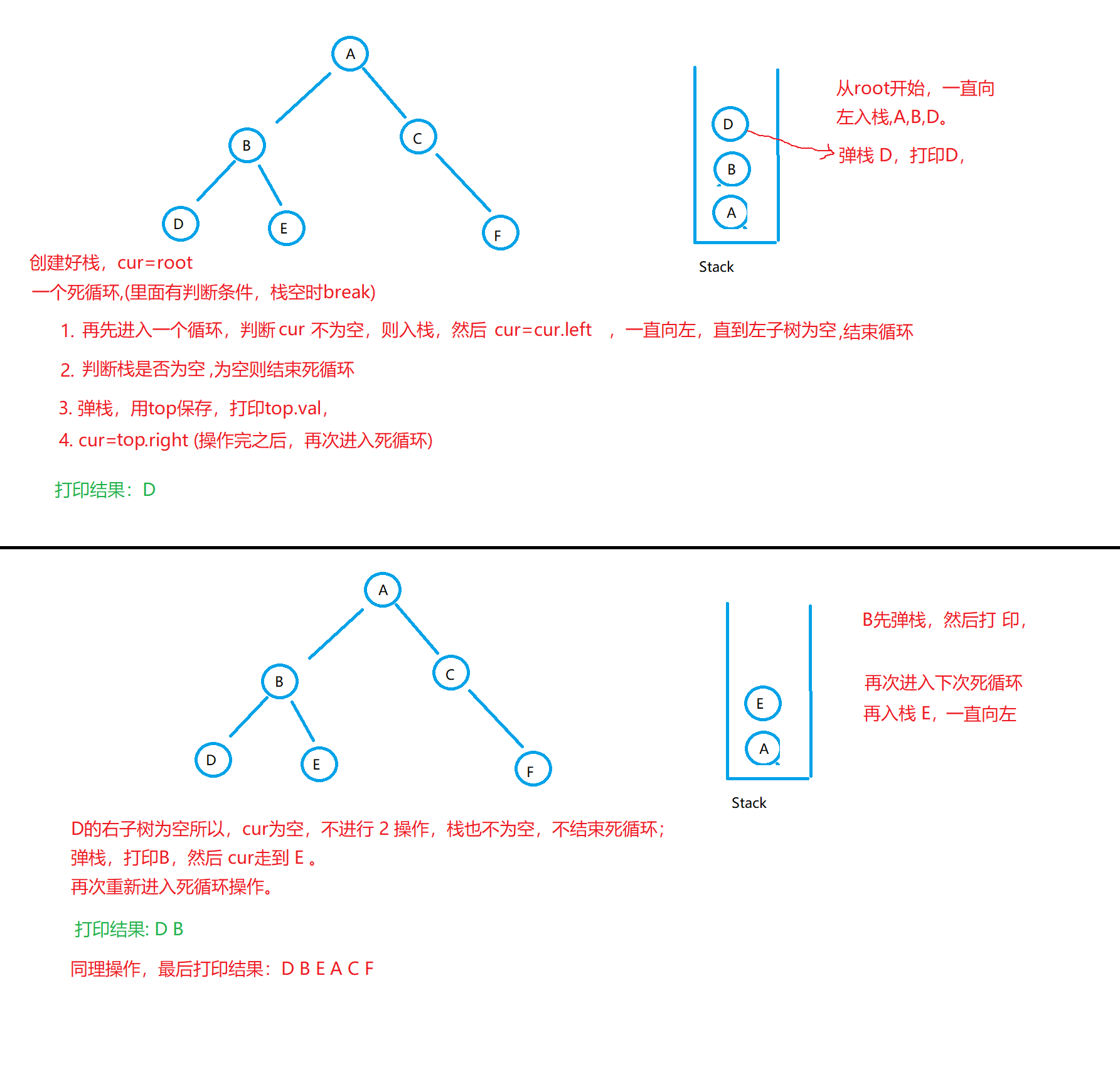
code
recursion
public static void inOrder(Node root){
//The root node is empty and ends directly
if(root==null){
return;
}
//Left subtree
inOrder(root.left);
//Root node
System.out.print(root.val+" ");
//Right subtree
inOrder(root.right);
}
iteration
public static void inOrder(TreeNode root){
//The root node is empty and ends directly
if(root==null){
return;
}
Stack<TreeNode> s=new Stack<>();
TreeNode cur=root;
while (true){
//Look to the left and put it in the stack
while (cur!=null){
s.push(cur);
cur=cur.left;
}
//If the stack is empty, the traversal ends
if(s.empty()){
break;
}
//Get stack top element access
TreeNode top=s.pop();
System.out.print(top.val+" ");
//Repeat the above operation from the right subtree of the current node
cur=top.right;
}
}
3, Postorder traversal
thinking
Recursion: first root the left subtree, then the right subtree, and then the root node.
Iteration: the idea of post order is similar to that of middle order, with one difference,
When taking the top element of the stack, it is peek (), depending on whether the top element of the stack has a right subtree or whether the right subtree has been accessed. If there is no right subtree or it has been accessed, it will be directly printed on the pop-up stack.
Other operations are the same as those in the middle sequence. You can understand them by looking at the code.
code
recursion
public static void postOrder(Node root){
//The root node is empty and ends directly
if(root==null){
return;
}
//Left subtree
postOrder(root.left);
//Right subtree
postOrder(root.right);
//Root node
System.out.print(root.val+" ");
}
iteration
public static void postOrder(TreeNode root){
//The root node is empty and ends directly
if(root==null){
return;
}
Stack<TreeNode> s=new Stack<>();
TreeNode cur=root;
TreeNode prev=null;
while (true){
//Look to the left and put it in the stack
while (cur!=null){
s.push(cur);
cur=cur.left;
}
//If the stack is empty, the traversal ends
if(s.empty()){
break;
}
//Take out the top element of the stack to see if it can be accessed
TreeNode top=s.peek();
//The right subtree of the stack top element is empty or has been accessed
if(top.right==null||top.right==prev){
System.out.println(top.val+" ");
s.pop();
//Keep it good. prve is the last element that has been traversed (this detail is very important) to judge whether it has been accessed
prev=top;
}else {
cur=top.right;
}
}
}
4, Sequence traversal
thinking
Recursion: take question 102 of force buckle as an example.
Iteration: operate with queues. Enter the queue first and enter the loop (end condition, queue is empty).
1.cur saves out of queue elements and prints val.
2. If cur.left is not empty, join the team.
3. If cur.right is not empty, join the team.
Re operate the cycle. End the loop until the queue is empty.
code
recursion
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result=new ArrayList<>();
//The root node is empty and ends directly
if(root==null){
return result;
}
helper(root,0,result);
return result;
}
private void helper(TreeNode root, int level,List<List<Integer>> result) {
//When the accessed row does not correspond in the result, a row is added
if(level==result.size()){
result.add(new ArrayList<>());
}
//get accesses the row, add adds the element val
result.get(level).add(root.val);
//Visit left
if(root.left!=null){
helper(root.left,level+1,result);
}
//Access right
if(root.right!=null){
helper(root.right,level+1,result);
}
}
iteration
public static void levelOrder(Node root){
//The root node is empty and ends directly
if(root==null){
return;
}
Queue<Node> queue=new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
Node cur=queue.poll();
System.out.print(cur.val+" ");
//Judge left subtree
if(cur.left!=null){
queue.offer(cur.left);
}
//Judge right subtree
if(cur.right!=null){
queue.offer(cur.right);
}
}
}