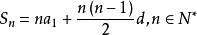Problem description
Time Limit: 1.0s Memory Limit: 256.0MB
Long ago, the Kingdom of T flourished unprecedentedly. In order to better manage the country, the Kingdom built a large number of expressways to connect the capital and the major cities in the kingdom.
In order to save money, the ministers of State T, after thinking about it, formulated a set of excellent construction plans, so that any big city can arrive directly from the capital or indirectly through other big cities. At the same time, if you don't repeat your journey through big cities, the only way to get from the capital to each big city is through the capital.
J is an important Minister of State T. He inspects the cities and observes the people's conditions. So, going from one city to another has become J's most common thing. He has a purse to keep the fares between cities.
Smart J finds that if he doesn't stop and trim in a city, he spends so much on his journey that he has traveled the distance he has traveled. In the kilometer from X km to x+1 km (x is an integer), he spends so much on his journey. That is to say, it costs 11 to walk 1 kilometer and 23 to walk 2 kilometers.
Minister J wants to know: what is the maximum possible cost of traveling from one city to another without rest?
Input format
The first line of input contains an integer n, representing the number of cities in Kingdom T, including the capital.
Cities are numbered from the beginning, with No. 1 as the capital.
Next line n-1 describes the highway in Country T (the highway in Country T must be n-1)
Three integers, Pi, Qi and Di, in each row, indicate that there is a highway between the city Pi and Qi, the length of which is Di kilometers.
Output format
Output an integer to indicate the maximum cost of travel by Minister J.
Sample input 1
5
1 2 2
1 3 1
2 4 5
2 5 4
Sample output 1
135
Output format
Minister J spends 135 fees from City 4 to City 5.
This is the result of my evaluation (some codes on the Internet have only 75 points because the last test data is 10,000 points too large):

thinking
The surface of the title is the toll, but the toll is an equal difference series. The longer the path, the more the cost, so we need to find the two longest distances first.
Some ideas are also mentioned in the abstract:
Firstly, the adjacency matrix is used to store the graph to reduce the space complexity and time complexity.
Core ideas:
The key to solve this problem is to use the dijkstra algorithm twice. You need to know that "assuming that the farthest point from point a is point B and the farthest point from point B is point c, then the farthest two points of the whole graph are affirmative b-c." PS:(c can be equal to a or not a)"
We can find the farthest point b from a point (I take 1) by the first dijkstra algorithm, and then find the farthest point c from b by the first dijkstra algorithm. So we get the longest distance bc.
Then the sum of equal difference series is equal to (11+10+bc)*bc/2.
You can also sum with this sequence of equals and differences.
Code
import java.util.Iterator; import java.util.LinkedList; import java.util.List; import java.util.PriorityQueue; import java.util.Scanner; public class Dijkstra { static int nodenum = 0; static List<dist>[] nextmattrix; static class dist implements Comparable<dist> { int index; int value; public dist(int i, int v) { this.index = i; this.value = v; } //The larger the priority queue comparison function is, the higher the priority queue comparison function is. @Override public int compareTo(dist o) { if (o.value == this.value) return 0; return (this.value > o.value) ? -1 : 1;// Big priorities } } //Dijkstra algorithm for priority queue edition (note that maximum distance is somewhat different from other dijkstra) public static int[] dijkst(int origin) { PriorityQueue<dist> prioqueue = new PriorityQueue<>(); int[] dis = new int[nodenum + 1]; dis[origin] = 0; prioqueue.add(new dist(origin, 0)); boolean[] select = new boolean[nodenum + 1]; while (!prioqueue.isEmpty()) { dist temp = prioqueue.poll(); select[temp.index] = true; Iterator<dist> tempnext = nextmattrix[temp.index].iterator(); dist nextvalue; int sum; while (tempnext.hasNext()) { nextvalue = tempnext.next(); int i = nextvalue.index; if (select[i]) continue; sum = dis[temp.index] + nextvalue.value; if ((dis[i] < sum)) { dis[i] = sum; prioqueue.add(new dist(i, dis[i])); } } } return dis; } public static void main(String[] args) { Scanner input = new Scanner(System.in); nodenum = input.nextInt(); nextmattrix = new List[nodenum + 1]; //Constructing Adjacency Matrix for (int i = 1; i < nodenum; i++) { int first = input.nextInt(); int second = input.nextInt(); int value = input.nextInt(); if (nextmattrix[first] == null) nextmattrix[first] = new LinkedList<>(); nextmattrix[first].add(new dist(second, value)); if (nextmattrix[second] == null) nextmattrix[second] = new LinkedList<>(); nextmattrix[second].add(new dist(first, value)); } input.close(); //Find the farthest point from 1 maxpoint int[] dis = dijkst(1); int maxpoint = 0; int max = 0; for (int i = 1; i <= nodenum; i++) if (dis[i] > max) { max = dis[i]; maxpoint = i; } //Find the furthest distance from maxpoint dis = dijkst(maxpoint); for (int i = 1; i <= nodenum; i++) if (dis[i] > max) { max = dis[i]; } //Summation of equal difference series for calculating road fare System.out.println((11 + 10 + max) * max / 2); } }