Following a blog post, after the Theta S camera was connected to the ROS system, the image matrix was published on the / image_raw topic. Let's start the file libuvc_camera.launch in the previous blog. At this time, the image has been transferred to the / image_raw topic. Open a new terminal and use the rostopic list to check the existing topic.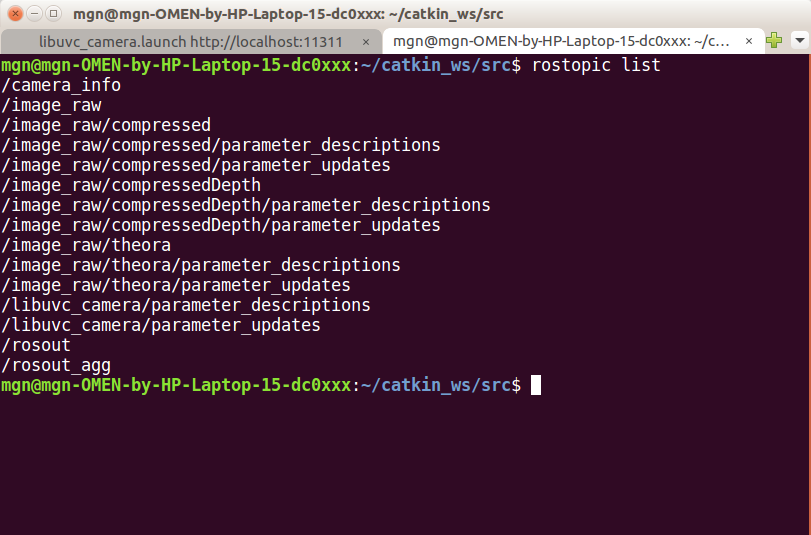
Image information is on the topic of / image · raw. Write a program like this to subscribe. The original image can be seen as follows.

#!/usr/bin/env python2.7
# -*- coding: utf-8 -*
import rospy
from sensor_msgs.msg import Image
import cv2
import cv_bridge


class Follower:
  def __init__(self):
    self.bridge = cv_bridge.CvBridge()
    self.image_sub = rospy.Subscriber('/image_raw', Image, self.image_callback)

  def image_callback(self,msg):
    image = self.bridge.imgmsg_to_cv2(msg,desired_encoding='bgr8')
    cv2.imshow("a",image)
    cv2.waitKey(1)
    
rospy.init_node('follower_1')
follower = Follower()
rospy.spin()

However, such an image is not a panoramic image, but a fish eye image of the front and back lenses of Theta S camera. Two images need to be transformed. There are several specific methods found on a Japanese blog (5 in total). The mathematical principle is not understood carefully, but the python program written by the blogger is inefficient (basically all for loops), and the real-time transformation effect is not good. I used numpy to improve the conversion speed of every picture, which is 16 times faster. The procedure is as follows.

#!/usr/bin/env python2.7
# -*- coding: utf-8 -*
import rospy
from sensor_msgs.msg import Image
import cv2
import cv_bridge
import numpy as np


class Follower:
  def __init__(self):
    self.bridge = cv_bridge.CvBridge()
    self.image_sub = rospy.Subscriber('/image_raw', Image, self.image_callback)

  def image_transfer(self, img):
    self.vertex = 640
    self.src_cx = 319
    self.src_cy = 319
    self.src_r = 283
    self.src_cx2 = 1280 - self.src_cx

    map_x = np.zeros((self.vertex, self.vertex*2))
    map_y = np.zeros((self.vertex, self.vertex*2))

    range_arr_y = np.array([range(self.vertex)])
    range_arr_x = np.array([range(self.vertex*2)])
    phi1 = (np.pi * range_arr_x) / self.vertex
    theta1 = (np.pi * range_arr_y.T) / self.vertex

    X = np.sin(theta1) * np.cos(phi1)
    Y = np.sin(theta1) * np.sin(phi1)
    Z = np.cos(theta1)

    phi2 = np.arccos(- X)
    theta2 = np.sign(Y) * np.arccos(-Z/np.sqrt(Y*Y + Z*Z))

    # Equidistant projection
    map_x = np.squeeze(np.where([phi2 < np.pi / 2], self.src_r * (phi2 / np.pi * 2) * np.cos(theta2) + self.src_cx\
    , self.src_r * ((np.pi - phi2)/np.pi * 2) * np.cos(np.pi - theta2) + self.src_cx2))
    map_y = np.squeeze(np.where([phi2 < np.pi / 2], self.src_r * (phi2 / np.pi * 2) * np.sin(theta2) + self.src_cy\
    , self.src_r * ((np.pi - phi2)/np.pi * 2) * np.sin(np.pi - theta2) + self.src_cy))

    # Stereoscopic projection
    # map_x = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (np.tan((phi2) / 2)) * np.cos(theta2) + src_cx\
    # , src_r * (np.tan((np.pi - phi2) / 2)) * np.cos(np.pi - theta2) + src_cx2))
    # map_y = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (np.tan((phi2) / 2)) * np.sin(theta2) + src_cy\
    # , src_r * (np.tan((np.pi - phi2) / 2)) * np.sin(np.pi - theta2) + src_cy))

    # Stereoscopic projective inverse transformation
    # map_x = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (1 - np.tan((np.pi / 2 - phi2) / 2)) * np.cos(theta2) + src_cx\
    # , src_r * (1 - np.tan((-np.pi/2 + phi2) / 2)) * np.cos(np.pi - theta2) + src_cx2))
    # map_y = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (1 - np.tan((np.pi / 2 - phi2) / 2)) * np.sin(theta2) + src_cy\
    # , src_r * (1 - np.tan((-np.pi/2 + phi2) / 2)) * np.sin(np.pi - theta2) + src_cy))
 
    # Orthography
    # map_x = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (np.sin(phi2)) * np.cos(theta2) + src_cx\
    # , src_r * (np.sin(np.pi - phi2)) * np.cos(np.pi - theta2) + src_cx2))
    # map_y = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (np.sin(phi2)) * np.sin(theta2) + src_cy\
    # , src_r * (np.sin(np.pi - phi2)) * np.sin(np.pi - theta2) + src_cy))

    #Positive projective inverse commutation
    # map_x = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (1 - np.sin(np.pi / 2 - phi2)) * np.cos(theta2) + src_cx\
    # , src_r * (1 - np.sin(- np.pi / 2 + phi2)) * np.cos(np.pi - theta2) + src_cx2))
    # map_y = np.squeeze(np.where([phi2 < np.pi / 2], src_r * (1 - np.sin(np.pi / 2 - phi2)) * np.sin(theta2) + src_cy\
    # , src_r * (1 - np.sin(- np.pi / 2 + phi2)) * np.sin(np.pi - theta2) + src_cy))
 
    map_x = map_x.astype('float32')
    map_y = map_y.astype('float32')

    img = cv2.remap( img, map_x, map_y, cv2.INTER_LINEAR, cv2.BORDER_CONSTANT)
    img = cv2.resize(img, (0, 0), fx=0.7, fy=0.7, interpolation=cv2.INTER_CUBIC) 
    return img

  def image_callback(self,msg):
    image = self.bridge.imgmsg_to_cv2(msg,desired_encoding='bgr8')
    image = self.image_transfer(image)
    cv2.imshow("a",image)
    cv2.waitKey(1)

rospy.init_node('follower_1')
follower = Follower()
rospy.spin()

There are 5 transformation methods in total. After I try these methods, I feel that isometric photography is the best one. The picture is also much more continuous, with a little delay later, within the acceptable range.
The renderings are as follows.

It becomes panoramic, and then it can do image processing, object recognition and so on, ha ha.

Here, the opencv version is very important. PIP2 install opencv python = = version number. This version number is very important. Remember that there was a problem with the cv2.remap() function in the previous 4 versions. PIP2 uninstall opencv python = = version number uninstalls the current version and installs the version with more than 3 points. Sometimes, the cv2.imshow() function has a problem. The image does not always show the problem Come out. Anyway, if the 3-point-plus version doesn't work, try uninstalling the 3-point-plus version. Add this section to the program if you want to query your version.

print(cv2.__version__)

The opencv version of my computer is 3.3.0.x. I have forgotten how much this x is. The terminal displays the third place.