Topological ranking can be used to determine whether there are loops in directed acyclic graph (DAG), and it can be used to judge whether a project with a sequence relationship can go smoothly.

1. Directed acyclic graphs (DAG)

A digraph without a loop is called a Directed Acycline Graph, or DAG graph for short.
There are two ways to judge whether a graph has a loop or not:

• For undirected graphs, if the backside (that is, the edge pointing to the vertex that has been visited) is encountered during depth-first traversal, there must be a loop.
• For a digraph, the topological ordering sequence of its vertices can be constructed. If all vertices in the graph are in its topological ordering sequence, there is no loop.

2. Topological Sorting

2.1 Concept of Topological Sorting

Topological Sort ** is a partial order on a set to obtain a total order on that set.
(Partial order means that only some members of a set of values can be compared, while total order means that all members of a set can be compared.)

2.2. Basic Ideas of Topological Sorting

The algorithm of topological sorting is as follows:

• 1) Select a vertex output without a precursor (entry 0) in the digraph;
• 2) Delete the vertex and all arcs tailed by it from the graph.
• 3) Repeat (1) (2) until all vertices have been output, or until there are no vertices without precursors in the current graph.
  The latter case indicates the existence of rings in a digraph.

3. Realization of Topological Sorting

3.1 Realization of Adjacency Table of Directed Graph

If the adjacency table is used as the storage structure of digraph, an array of vertex entries can be added to the header node array. A vertex with zero entries is a vertex without a precursor. The operation of deleting vertex with its tail can be equivalent to the operation of reducing the entrance of an arc-head equivalent point by 1.
At the same time, in order to avoid repeated detection of vertices with zero entry, a stack can be set up to store all vertices with zero entry.

Adjacent Table Storage of 3.1.1 Graph

Adjacency table definition

typedef struct node {
	//Side Node
	int adjvex;  // Vertex subscript
	struct node* nextarc; // Point to the next vertex
}node;
typedef struct headNode{
	// header node
	int indegree; // Penetration
	string info; // Vertex information, such as names
	node* firstarc; // First Adjacent Point
}headNode,Adjlist[MAX_VERTEX_NUM];
// Adjacency table
typedef struct {
	Adjlist vertex;   // Header node table
	int vexnum, arcnum;  // Number of points and edges
}ALGraph;

Create adjacency tables

void createALGraph(ALGraph &G) {// Create adjacency tables
	printf("Number of input vertices and edges:\n");
	cin >> G.vexnum >> G.arcnum;
	printf("Input vertex information:\n");
	for (int i = 0; i < G.vexnum; i++) {
		cin >> G.vertex[i].info;
		G.vertex[i].indegree = 0;
		G.vertex[i].firstarc = NULL;
	}
	printf("Input side information to V1->V2 Form:\n");
	for (int i = 0; i < G.arcnum; i++) {
		string v1, v2;
		cin >> v1 >> v2;
		int index1 = Locate(G, v1);
		int index2 = Locate(G, v2);
		G.vertex[index2].indegree += 1;
		// Inserting new nodes using header interpolation
		node* temp = new node;
		temp->adjvex = index2;
		temp->nextarc = G.vertex[index1].firstarc;
		G.vertex[index1].firstarc = temp;
	}
} 

Find the subscript of a node in the adjacent table

int Locate(ALGraph G, string v) {
	int i = 0;
	for (; i < G.vexnum && G.vertex[i].info != v; i++);
	if (i == G.vexnum) return -1;
	else return i;
}

Topological sorting of 3.1.2 adjacency tables

int TopoSort(ALGraph G) {
	// Indegree [0. vexnum-1] for each vertex 
	// If the graph is initialized, it can be omitted
	//FindInDegree(G, indegree);
	stack<int> s; // Subscription of Nodes with Degree 0
	for (int i = 0; i < G.vexnum; i++) {
		if (G.vertex[i].indegree == 0) s.push(i);
	}
	// Nodes that do not print zero
	int count = 0;// Nodes that are currently printed
	while (!s.empty()) {
		int j = s.top(); s.pop();
		//printf("currently found vertex% d", j);
		count++;
		//cout << G.vertex[j].info << "-->" << endl;
		printf("%s-->",G.vertex[j].info.c_str());
		// Delete the arc ending at this node
		node* temp = G.vertex[j].firstarc;
		while (temp) {
			int index = temp->adjvex;
			G.vertex[index].indegree--;
			if (G.vertex[index].indegree == 0) s.push(index);
			temp = temp->nextarc;
		}
	}
	if (count < G.vexnum) return 0; // Ring Road
	else return 1; // loop-free
}

3.2 Realization of Adjacency Matrix of Directed Graph

Adjacency Matrix Storage of 3.2.1 Graphs

Definition of Adjacency Matrix

#define MAX_VERTEX_NUM 20 // Maximum number of vertices
// Define adjacency matrix
typedef int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //0 or 1 denotes adjacency
typedef struct {
	AdjMatrix matrix;
	string vexs[MAX_VERTEX_NUM]; // Vertex vector
	int indegree[MAX_VERTEX_NUM]; // Initiation of vertices
	int vexnum, arcnum; // Number of vertices and edges
}MGraph;

Creation of Adjacency Matrix

void createMGraph(MGraph &G) {
	int i, j;
	printf("Number of input vertices and edges:\n");
	cin >> G.vexnum >> G.arcnum;
	// Initialization of adjacency matrix
	for (i = 0; i < G.vexnum; i++) {
		G.indegree[i] = 0;
		for (j = 0; j < G.vexnum; j++) G.matrix[i][j] = 0;
	}
	printf("Input vertex information\n");
	for (i = 0; i < G.vexnum; i++) cin >> G.vexs[i];
	printf("Information on input side Vi-->Vj\n");
	for (i = 0; i < G.arcnum; i++) {
		string v1, v2;
		cin >> v1 >> v2;
		int l1 = LocateVex(G, v1);
		int l2 = LocateVex(G, v2);
		G.matrix[l1][l2] = 1;
		G.indegree[l2]++;
	}
}

Vertex Location

int LocateVex(MGraph G, string u) {
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != u; i++);
	if (i == G.vexnum) return -1;
	else return i;
}

Topological Sorting of 3.2.2 Adjacent Matrix

int TopoSort(MGraph G) {
	int i, j;
	stack<int> s;
	for (i = 0; i < G.vexnum; i++) {
		if (G.indegree[i] == 0) s.push(i);
	}
	int count = 0; // Sorted vertices
	while (!s.empty()) {
		j = s.top(); s.pop();
		count++;
		cout << G.vexs[j] << "-->";
		for (int k = 0; k < G.vexnum; k++) {
			if (G.matrix[j][k] == 1) {
				if (!(--G.indegree[k])) s.push(k); // Delete arc
			}
		}
	}
	if (count == G.vexnum) return 0;
	else return 1;
}

3.3 Test Cases

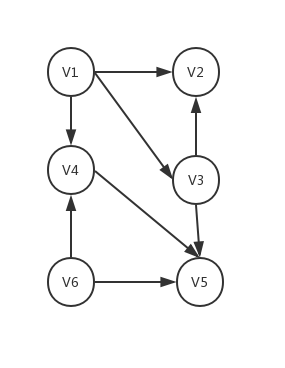
6 8
V1 V2 V3 V4 V5 V6 
V1 V2
V1 V4
V1 V3
V3 V2
V3 V5
V4 V5
V6 V4
V6 V5

3.4 Topological Sorting Based on Depth First

When there are no rings in a digraph, the depth-first traversal can be used for topological sorting, i.e. the depth-first traversal from a certain point.
The vertex that first exits the depth-first traversal, i.e. the vertex with a degree of 0, is the last vertex in the sequence of topological sorting.
Therefore, the vertex sequence is recorded in the order of exiting DFS, and then output in reverse order.

#include <iostream>
#include <string>
#include<stack>
using namespace std;

#define MAX_VERTEX_NUM 20 // Maximum number of vertices
// Define adjacency matrix
typedef int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //0 or 1 denotes adjacency
typedef struct {
	AdjMatrix matrix;
	string vexs[MAX_VERTEX_NUM]; // Vertex vector
	int indegree[MAX_VERTEX_NUM]; // Initiation of vertices
	int vexnum, arcnum; // Number of vertices and edges
}MGraph;

//Graph Creation
void createMGraph(MGraph &G);
// Vertex Location
int LocateVex(MGraph G, string v);
// Return the first adjacent point of u in graph G
int First(MGraph g, int u);
// Next Adjacent Point of V relative to u in Return Graph G
int Next(MGraph G, int v, int u);
// Topological Sorting
void DFS_Master(MGraph G);
void DFS(MGraph G, int v, int* visited, stack<int> &s);
int main() {
	MGraph G;
	createMGraph(G);
	DFS_Master(G);
	system("pause");
	return 0;
}
void DFS_Master(MGraph G) {
	// Initialize access nodes
	int i, j;
	int* visited = new int[G.vexnum];
	// Inverse Sequence Node
	stack<int> s;
	for (i = 0; i < G.vexnum; i++) visited[i] = 0;
	for (i = 0; i < G.vexnum; i++) {
		if (!visited[i]) DFS(G, i, visited,s);
	}
	while (!s.empty()) {
		j = s.top(); s.pop();
		cout << G.vexs[j] << "-->";
	}
	delete[] visited;
}
void DFS(MGraph G, int v, int* visited,stack<int> &s) {
	visited[v] = 1;
	printf("Visit%d node", v);
	int i;
	for (i = First(G, v); i != -1; i = Next(G, v, i)) {
		if (!visited[i]) DFS(G, i, visited, s);
	}
	// If v has no adjacent point i, it exits
	s.push(v);
}
void createMGraph(MGraph &G) {
	int i, j;
	printf("Number of input vertices and edges:\n");
	cin >> G.vexnum >> G.arcnum;
	// Initialization of adjacency matrix
	for (i = 0; i < G.vexnum; i++) {
		G.indegree[i] = 0;
		for (j = 0; j < G.vexnum; j++) G.matrix[i][j] = 0;
	}
	printf("Input vertex information\n");
	for (i = 0; i < G.vexnum; i++) cin >> G.vexs[i];
	printf("Information on input side Vi-->Vj\n");
	for (i = 0; i < G.arcnum; i++) {
		string v1, v2;
		cin >> v1 >> v2;
		int l1 = LocateVex(G, v1);
		int l2 = LocateVex(G, v2);
		G.matrix[l1][l2] = 1;
		G.indegree[l2]++;
	}
}

int LocateVex(MGraph G, string u) {
	int i;
	for (i = 0; i < G.vexnum && G.vexs[i] != u; i++);
	if (i == G.vexnum) return -1;
	else return i;
}

int First(MGraph G, int u) {
	int i;
	for (i = 0; i < G.vexnum; i++) {
		if (G.matrix[u][i] != 0) break;
	}
	if (i == G.vexnum) return -1;  // No critical point
	else return i;
}

int Next(MGraph G, int v, int u) {
	int index;
	for (index = u + 1; index < G.vexnum && G.matrix[v][index] == 0; index++);
	if (index == G.vexnum) return -1;
	else return index;
}

Reference material

Yan Weimin, Data Structure C Language Edition