Bubble sort algorithm
Bubble sorting repeatedly traverses the sequence to be sorted, comparing two adjacent elements each time, and exchanging them if their order is wrong. Repeat the traversal until there is no need to exchange, indicating that the sequence has been sorted.
-
Algorithm steps:
-
Compare adjacent elements: if the first is larger than the second, exchange;
-
Traverse the first pair at the beginning to the last pair at the end, and execute step 1;
-
Repeat steps 1 to 2 until the sorting is completed.
-
-
Improved bubble sorting: the last element after the first sorting is the largest, so the next traversal only needs to be performed to the penultimate pair.
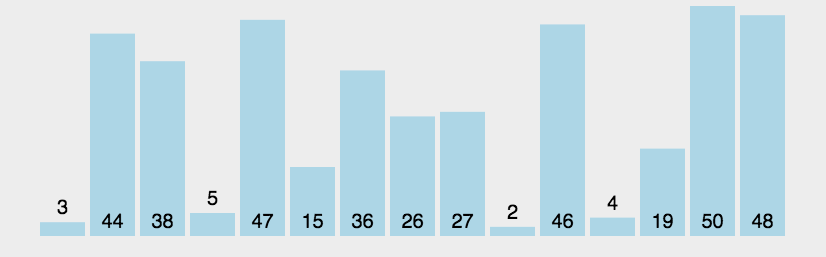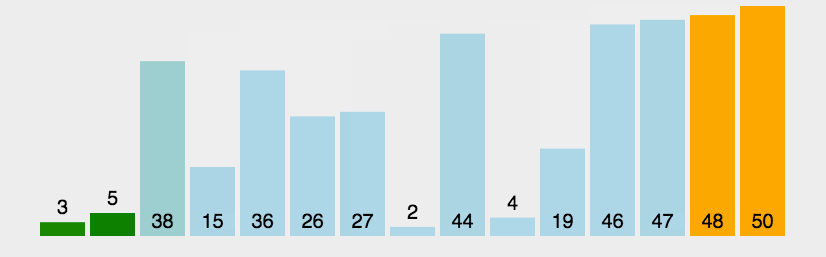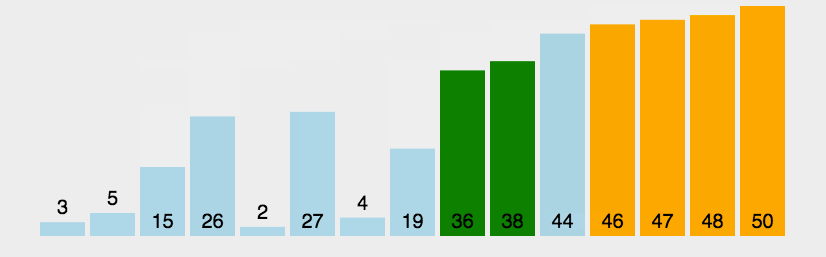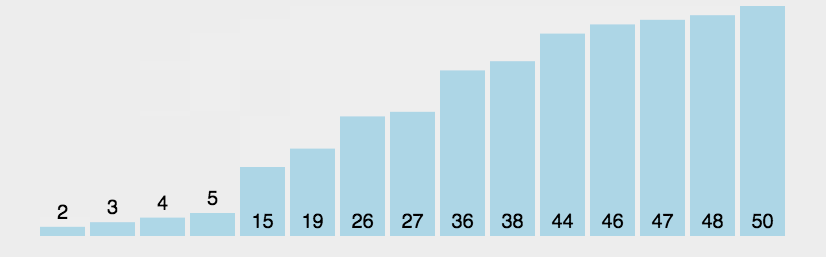
Main code:
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void sort_array(int *arr, int n)
// Programming implementation of bubble sorting algorithm: convert the out of order sequence arr into ascending sequence
// Function parameter: out of order integer array arr array length
// Output required: call print_array(int *arr, int n) outputs the sequence after the first three bubbling operations and the final ascending sequence
{
// Please supplement the code here to complete this task
/********** Begin *********/
for (int i=0; i<n; i++) {
for (int j=0; j<n-1-i; j++) {
if(arr[j]>arr[j+1]){
swap(arr[j], arr[j+1]);
}
}
if (i<3) {
print_array(arr, n);
}
}
print_array(arr, n);
/********** End **********/
}Select Sorting Algorithm
Selective sorting is a simple and intuitive sorting algorithm. First, find the smallest element in the unordered sequence and store it at the beginning of the sorted sequence. Then, continue to find the smallest element from the remaining unordered elements, and then put it at the end of the sorted sequence. And so on until all elements are sorted.
-
Algorithm steps:
-
Initial state: the disordered sequence is R[0,n − 1], the length is n, and the ordered region is empty;
-
The i=1,..,n − 1 order selects the smallest element R[k] from the current disordered region R[i − 1,n − 1] and exchanges it with the first record R[i − 1] of the disordered region, then R[0,i − 1] becomes a new ordered region with an increase of 1 in the number of elements, and R[i,n − 1] becomes a new disordered region with a decrease of 1 in the number of elements;
-
n − 1 Selection exchange is completed.
-
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void sort_array(int *arr, int n)
// Programming to realize the "selective sorting algorithm": convert the out of order sequence arr into ascending sequence
// Function parameter: array length of out of order integer array (no duplicate elements)
// Output required: call print_array(int *arr, int n) outputs the sequence after the first three selection operations and the final ascending sequence
{
// Please supplement the code here to complete this task
/********** Begin *********/
for (int i=0; i<n-1; i++) {
int minIdx = i;
for (int j=i+1; j<n; j++) {
if(arr[minIdx]>arr[j]){
minIdx = j;
}
}
swap(arr[i], arr[minIdx]);
// Exchange arr[i] and arr[minIdx]
if (i<3) {
print_array(arr, n);
}
}
print_array(arr, n);
/********** End **********/
}Insert sort algorithm
The working principle of insert sort is to build an ordered sequence. For unordered data, scan from back to front in the sorted sequence, find the corresponding position and insert.
-
Algorithm steps:
-
Starting from the first element, the element is considered to have been sorted;
-
Remove an element and scan from back to front in the sorted element sequence;
-
If the sorted element is larger than the new element, move the sorted element to the next position;
-
Repeat step 3 until the sorted element is found to be less than or equal to the position of the new element;
-
After inserting the new element into this position;
-
Repeat steps 2 to 5.
-
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void sort_array(int *arr, int n)
// Programming implementation of insertion sorting algorithm: convert the out of order sequence arr into ascending sequence
// Function parameter: array length of out of order integer array (no duplicate elements)
// Output required: call print_array(int *arr, int n) outputs the sequence after the first three insertion operations and the final ascending sequence
{
// Please supplement the code here to complete this task
/********** Begin *********/
for (int i=1; i<n; i++) {
int val = arr[i];
for (int j=i-1; j>=0; j--) {
if(val<arr[j]){
arr[j+1] = arr[j];
arr[j] = val;
}else{
break;
}
}
if(i<=3){
print_array(arr, n);
}
}
print_array(arr, n);
/********** End **********/
}Hill sorting algorithm
Hill sorting was invented by Shell in 1959, also known as reduced incremental sorting. It is the first sorting algorithm to break through O(n2). It belongs to an improved version of simple insertion sorting, and will give priority to the elements far away.
-
Algorithm steps:
-
Select an incremental sequence T1, T2,..., Tk, where Ti > TJ, Tk = 1, I > J;
-
For each sorting, the sequence to be arranged is divided into several subsequences according to the corresponding increment Ti, and each subsequence is directly inserted and sorted;
-
Sort the sequence k times according to the number of incremental sequences k.
-
-
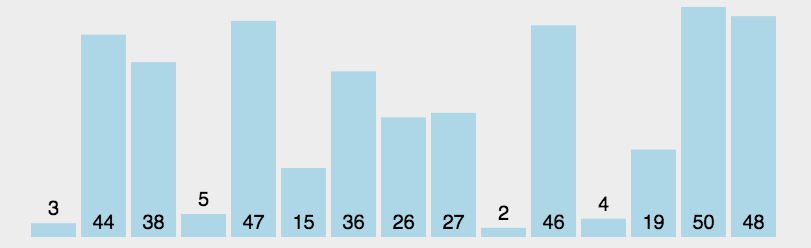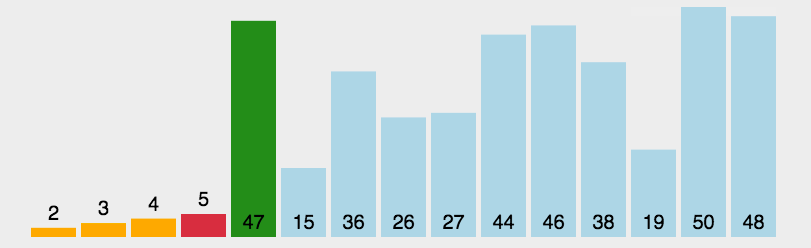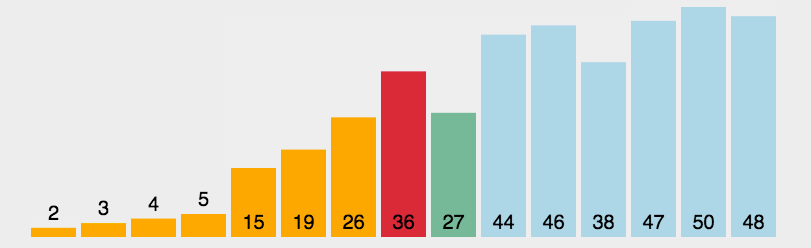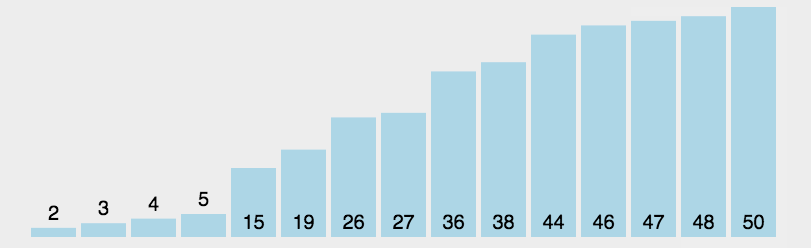
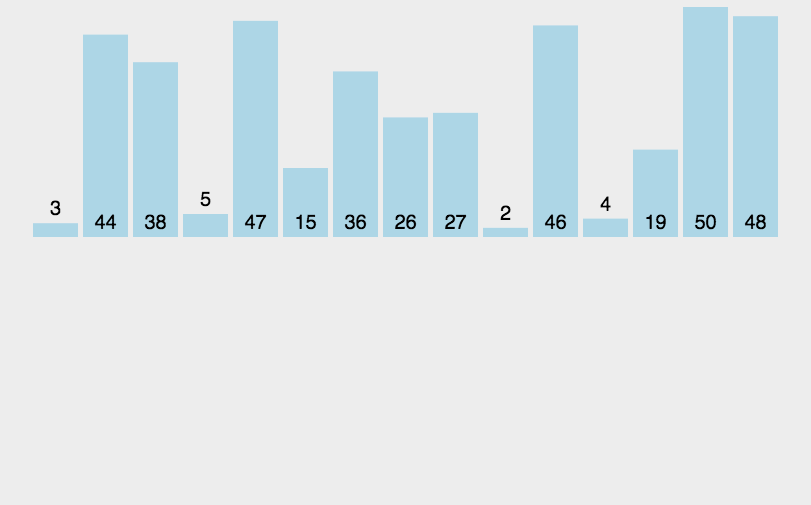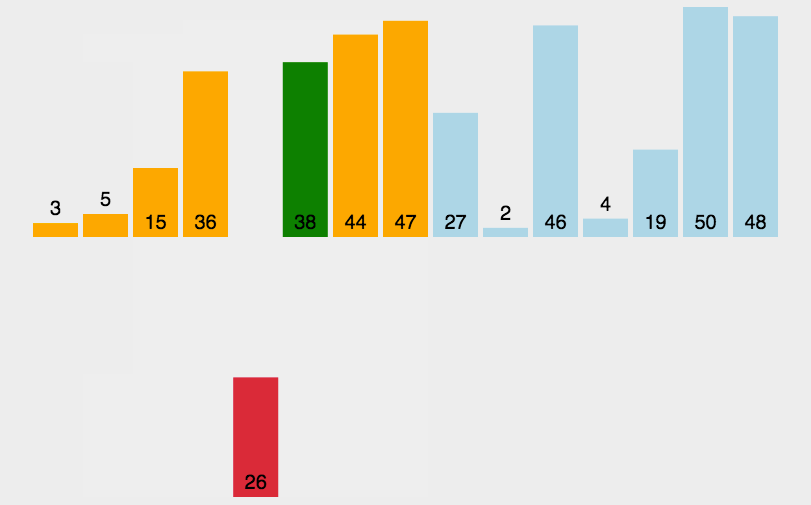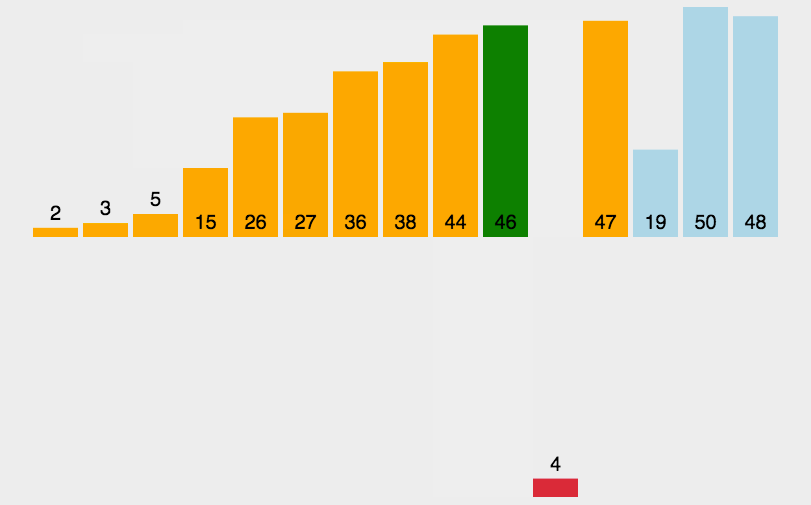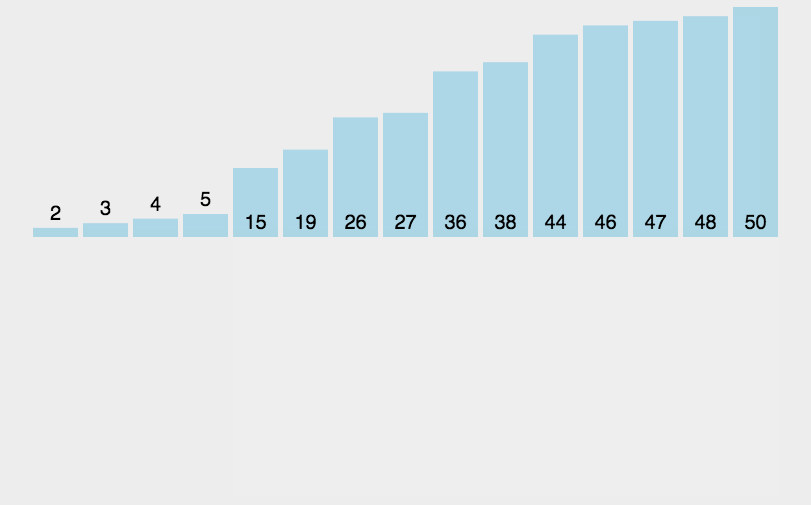
Hill sorting example: the incremental sequences in the following figure are: 5, 2, 1. The first sorting will insert the subsequence with increment of 5, the second sorting will insert the subsequence with increment of 2, and the third sorting will insert the subsequence with increment of 1, and finally complete the sorting.
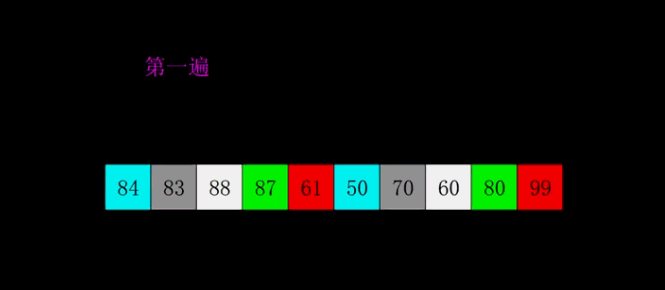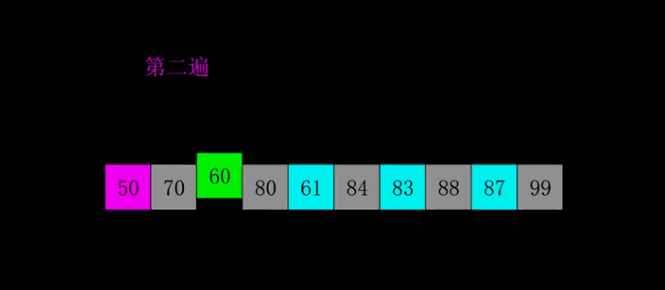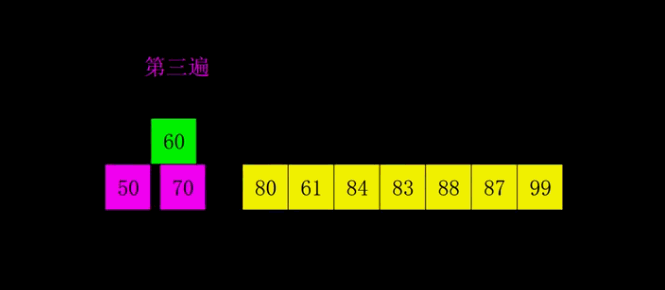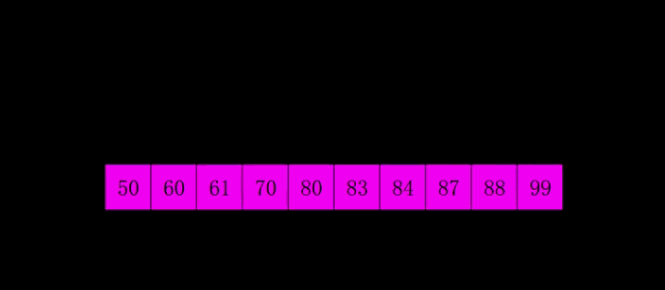
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void sort_array(int *arr, int n)
// Programming Hill sorting algorithm: convert the out of order sequence arr into ascending sequence
// Function parameter: out of order integer array length
// Output required: call print_array(int *arr, int n) outputs the sequence after three incremental sorting operations and the final ascending sequence
{
// Please supplement the code here to complete this task
/********** Begin *********/
int c=0,e,f=10;
for(int a=f/2;a>0;a=a/2)
{
for(int i=a;i<n;i++)
{
for(int d=i-a;d<n;d=d+a)
if(arr[i-a]>arr[d])
{
e=arr[d];
arr[d]=arr[i-a];
arr[i-a]=e;
}
}
c++;
if(c<=3)
print_array(arr, n);
}
print_array(arr, n);
/********** End **********/
}
Merge sort algorithm
Merge sort is a sort method based on the idea of merge. It is a very typical application of Divide and Conquer. Divide: divide the problem into some small problems and solve them recursively; Conquer: combine the answers obtained in different stages.
-
Algorithm steps:
-
The input sequence with length n is divided into two subsequences with length n/2;
-
The two subsequences are sorted by merging;
-
Merge two sorted subsequences into a final sorting sequence.
-
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
int* merge_array(int *arr1, int n1, int* arr2, int n2)
// The combination of two ordered arrays arr1 and arr2 is realized by programming
// Function parameters: ordered array arr1 array arr1 length ordered array arr2 array arr2 length
// Function return value: returns the merged array sorted from small to large
{
// Please supplement the code here to complete this task
/********** Begin *********/
int* arr = (int*)malloc(sizeof(int)*(n1+n2));
int p = 0;
int p1 = 0;
int p2 = 0;
while (p1<n1 || p2<n2) {
if(p1<n1 && p2<n2){
// The top-down recursive method makes the two arrays orderly
// Select two smaller arrays for arr
if (arr1[p1]<arr2[p2]) {
arr[p++] = arr1[p1++];
}else{
arr[p++] = arr2[p2++];
}
}else if(p1<n1){
// arr2 is finished, leaving arr1
arr[p++] = arr1[p1++];
}else if(p2<n2){
// arr1 is finished, leaving arr2
arr[p++] = arr2[p2++];
}
}
return arr;
/********** End **********/
}
int* merge_sort(int *arr, int n)
// Based on merge_array function programming for merging and sorting: a top-down recursive method
// Function parameter: ordered array arr length
// Function return value: returns the array sorted from small to large
{
// Please supplement the code here to complete this task
/********** Begin *********/
if(n==1){
return arr;
}
int m = n/2;
int* arr1 = (int*)malloc(sizeof(int)*(m));
int* arr2 = (int*)malloc(sizeof(int)*(n-m));
for (int i=0, j=0; i<m; i++, j++) {
// Left half array to arr1
arr1[j] = arr[i];
}
for (int i=m, j=0; i<n; i++, j++) {
// Right half array to arr2
arr2[j] = arr[i];
}
// Recursive subarray
arr1 = merge_sort(arr1, m);
arr2 = merge_sort(arr2, n-m);
// Merge subarrays
return merge_array(arr1, m, arr2, n-m);
/********** End **********/
}Quick sorting algorithm
Quick sort is the most commonly used sort algorithm, which is characterized by high speed and high efficiency. The basic idea of quick sort: select a key value as the benchmark value. Those smaller than the benchmark value are on the left (generally disordered), and those larger than the benchmark value are on the right (generally disordered). Generally, the first element of the sequence is selected as the reference value.
-
Algorithm steps:
-
Pick out an element from the sequence, which is called the benchmark pivot;
-
partition operation: elements smaller than the benchmark value are placed on the left, and elements larger than the benchmark value are placed on the right;
-
recursive: recursively sort the subsequences of elements smaller than the reference value and those larger than the reference value.
-
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
int partition_array(int *arr ,int l,int r)
// Programming arr[l, r] partition: select a benchmark. The left is smaller than the benchmark and the right is larger than the benchmark
// Return to the base position
{
// Please supplement the code here to complete this task
/********** Begin *********/
int m=arr[l];
while(r!=l)
{
for(r;r!=l;r--)
if(arr[r]<m)
{
arr[l]=arr[r];
break;
}
for(l;l!=r;l++)
if(arr[l]>m)
{
arr[r]=arr[l];
break;
}
}
arr[l]=m;
return l;
/********** End **********/
}
int* quick_sort(int *arr, int l, int r)
// Based on partition_array function programming for quick sorting: a top-down recursive method
// Function parameters: ordered array arr initial l=0, r=n-1
// Function return value: returns the array sorted from small to large
{
// Please supplement the code here to complete this task
/********** Begin *********/
if(l<r)
{
int p=partition_array(arr,l,r);
quick_sort(arr,l,p-1);
quick_sort(arr,p+1,r);
}
return arr;
/********** End **********/
}Heap sorting algorithm
Heap sort Heapsort is a sort algorithm designed by using heap data structure. Heap is a structure similar to a complete binary tree and satisfies the nature of heap: that is, the key value or index of a child node is always less than (or greater than) its parent node.
-
Algorithm steps:
-
The initial keyword sequence to be sorted (R1,R2,... Rn) is constructed into a large top heap, which is the initial unordered area;
-
Exchange the top element R[1] with the last element R[n], and a new disordered region (R1,R2,... Rn-1) and a new ordered region (Rn) are obtained, and R[1,2... N-1] < = R[n];
-
Since the new heap top R[1] may violate the nature of the heap after exchange, it is necessary to adjust the current unordered area (R1,R2,... Rn-1) to a new heap, and then exchange R[1] with the last element of the unordered area again to obtain a new unordered area (R1,R2,... Rn-2) and a new ordered area (Rn-1,Rn). Repeat this process until the number of elements in the ordered area is n-1, and the whole sorting process is completed.
-

void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void adjustHeap(int *arr, int param1, int j)
// Programming heap adjustment
{
// Please supplement the code here to complete this task
/********** Begin *********/
int temp = arr[param1];
for(int i = 2*param1 +1;i<= j;i = 2*i+1) //i is the left child subscript
{
//Determine whether there is a right child
if(i < j && arr[i] < arr[i+1]) //It means that there is a right child, and the left child is smaller than the right child
{
i++;
}
if(arr[i] > temp)
{
arr[param1] = arr[i];
param1 = i;
}
else
{
break;
}
}
arr[param1] = temp;
Counting sorting algorithm
Counting sort is not a sort algorithm based on comparison. Its core is to convert the input data values into keys and store them in the additional array space. As a sort with linear time complexity, count sort requires that the input data must be integers with a certain range.
-
Algorithm steps:
-
Find the largest and smallest elements in the array to be sorted;
-
Count the number of occurrences of each element with value i in the array and store it in item i of array C;
-
All counts are accumulated (starting from the first element in C, and each item is added to the previous item);
-
Reverse fill the target array: put each element i in item C(i) of the new array, and subtract 1 from C(i) for each element.
-
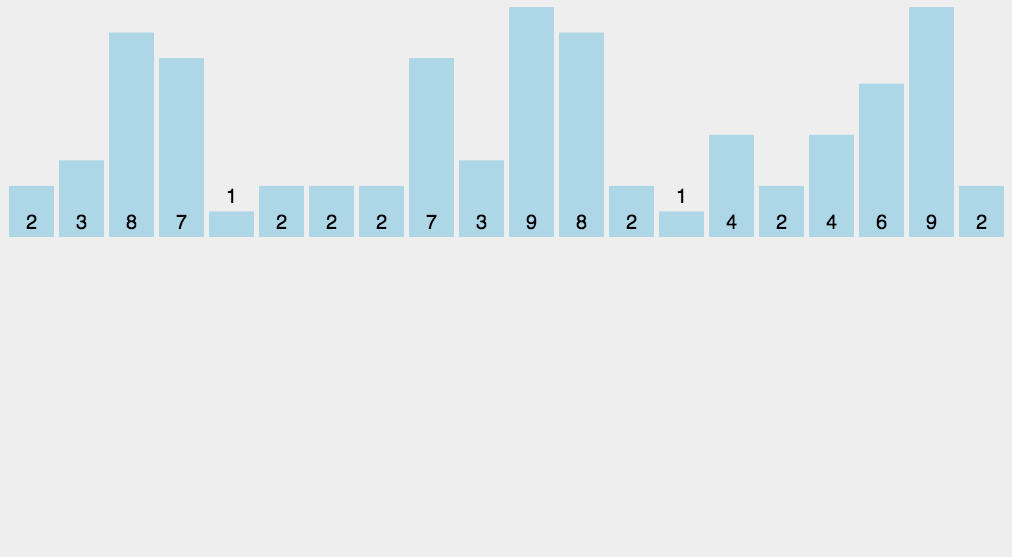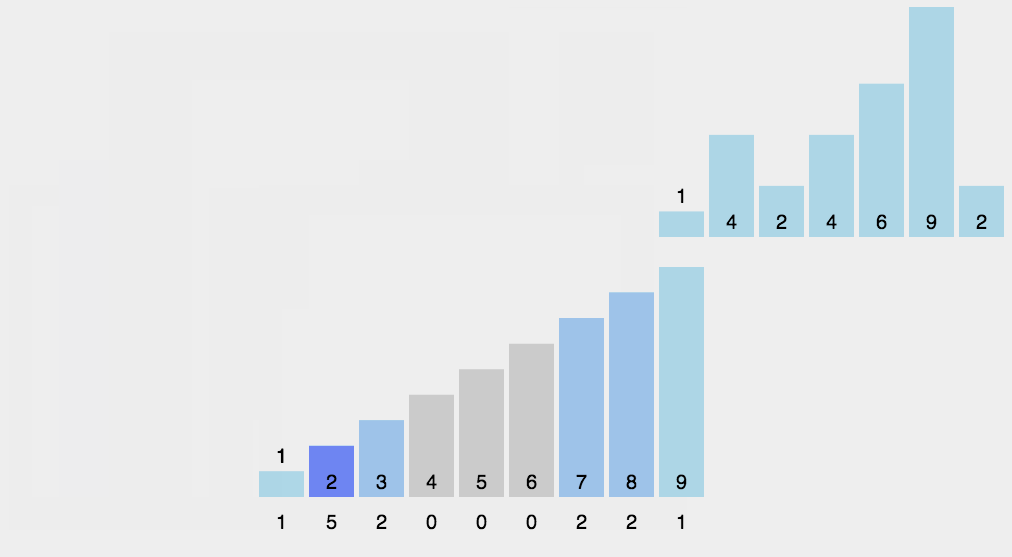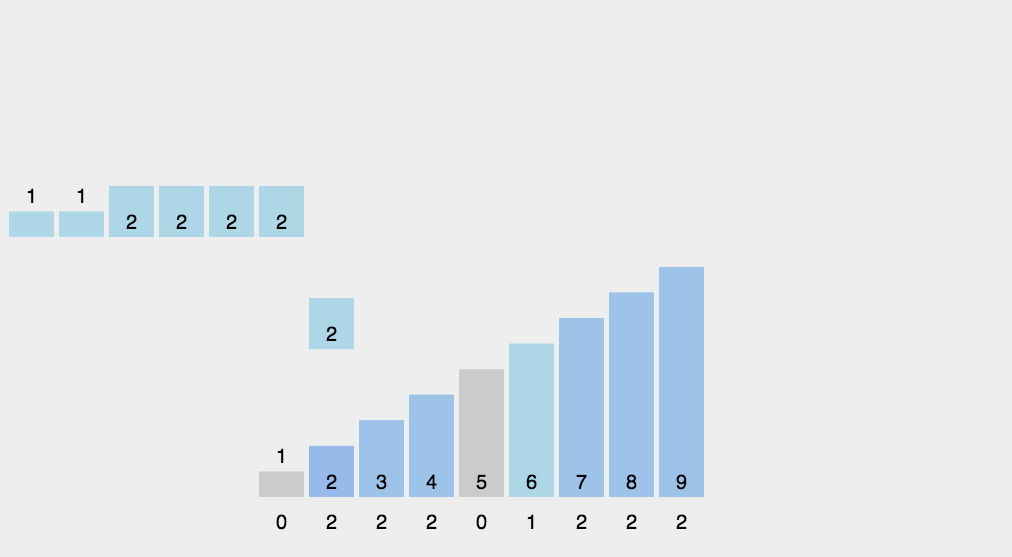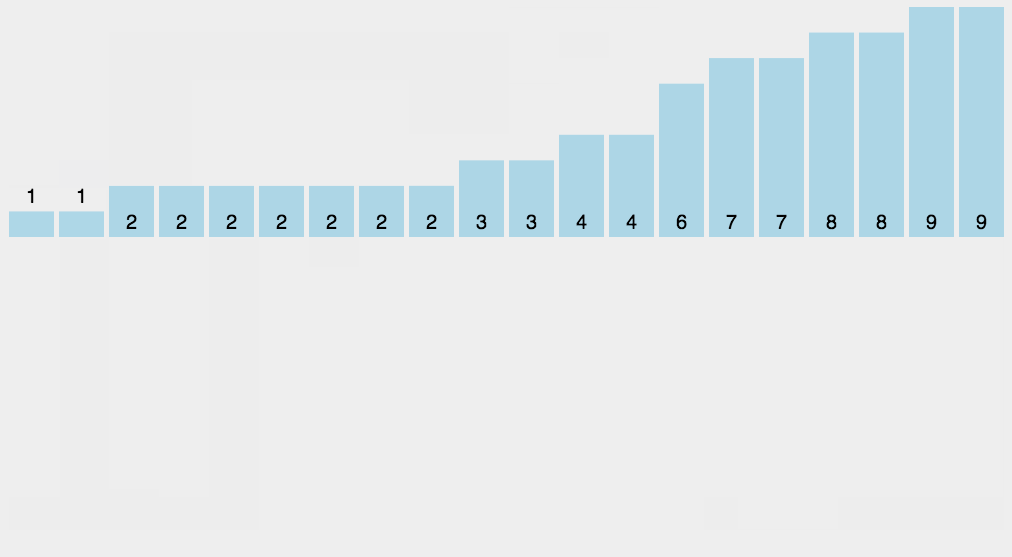
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
void sort_array(int *arr, int n)
// Programming implementation of counting sorting algorithm
// Function parameter: out of order integer array length
// Output required: call print_array(int *arr, int n) output:
// One element per line and its number (in ascending order), such as 1
// And the final ascending sequence
{
// Please supplement the code here to complete this task
/********** Begin *********/
// Array maximum
int maxVal = arr[0];
for (int i=1; i<n; i++) {
if(maxVal<arr[i]){
maxVal = arr[i];
}
}
// Request count array and initialize to 0
int* cnt = (int*)malloc(sizeof(int)*(maxVal+1));
for (int i=0; i<=maxVal; i++) {
cnt[i] = 0;
}
// Count arr array elements
for (int i=0; i<n; i++) {
cnt[arr[i]]++;
}
// Sequential output of counting results
for (int i=0, k=0; i<=maxVal; i++){
if (cnt[i]) {
printf("%d %d\n", i, cnt[i]);
}
for (int j=0; j<cnt[i]; j++) {
arr[k++] = i;
}
}
print_array(arr, n);
/********** End **********/
}Bucket sorting algorithm
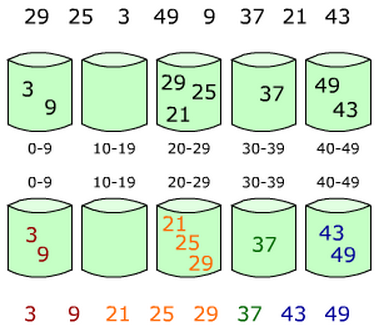
Bucket sorting is an upgraded version of counting sorting. It makes use of the mapping relationship of the function. The key to efficiency lies in the determination of the mapping function. Working principle of bucket sort: assuming that the input data is uniformly distributed, divide the data into a limited number of buckets, and sort each bucket separately (it is possible to use another sorting algorithm or continue to use bucket sorting recursively).
-
Algorithm steps:
-
Set a quantitative array as an empty bucket;
-
Traverse the input data and put the data into the corresponding bucket one by one;
-
Sort each bucket that is not empty;
-
Splice the ordered data from a bucket that is not empty.
-
void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
int* sort_array(int *arr, int n)
// Programming bucket sorting algorithm
// Function parameter: out of order integer array length
// Function return value: returns the array sorted from small to large
{
// Please supplement the code here to complete this task
/********** Begin *********/
int maxVal = arr[0];
for(int i = 1; i < n; i++) //Traverse the comparison, and assign the large one to maxVal
{
if(arr[i] > maxVal)
maxVal = arr[i];
}
int tmpArrLen = maxVal + 1;
int tmpArr[tmpArrLen]; //Get empty bucket size
int i, j;
for( i = 0; i < tmpArrLen; i++) //Empty bucket initialization
tmpArr[i] = 0;
for(i = 0; i < n; i++) //Search the sequence and put the items in the corresponding bucket one by one.
tmpArr[ arr[i] ]++;
for(i = 0, j = 0; i < tmpArrLen; i ++)
{
while( tmpArr[ i ] != 0) //Sort each bucket that is not empty.
{
arr[j ] = i; //Put items back into the original sequence from a bucket that is not empty.
j++;
tmpArr[i]--;
}
}
return arr;
/********** End **********/
}Cardinality sorting algorithm
Cardinality sorting is sorting according to the low order, and then collecting; Then sort according to the high order, and then collect; And so on until the highest order. Sometimes some attributes are prioritized. They are sorted first by low priority and then by high priority. The final order is the high priority, the high priority, the same high priority, and the low priority, the high priority.
-
Algorithm steps:
-
Get the maximum number in the array and get the number of bits;
-
arr is the original array, and each bit is taken from the lowest bit to form a radius array;
-
Count and sort the radix (using the characteristics that count sorting is suitable for a small range of numbers);
-

void print_array(int *arr, int n)
// Print array
{
if(n==0){
printf("ERROR: Array length is ZERO\n");
return;
}
printf("%d", arr[0]);
for (int i=1; i<n; i++) {
printf(" %d", arr[i]);
}
printf("\n");
}
int* sort_array(int *arr, int n)
// Programming implementation of cardinality sorting algorithm
// Function parameter: out of order integer array length
// Function return value: returns the array sorted from small to large
{
// Please supplement the code here to complete this task
/********** Begin *********/
int temp[10][n]={0}; //The first 10 represents 0 ~ 9, and the second 20 represents the size of a
int order[n]={0};
int i,j,k; //k represents the specific number in the current comparison
int t; //N = 1,101001000... Depends on the maximum number in a
int p;
t=1;
while(t <= 100)
{
for(i=0;i<n;i++)
{
k = (arr[i]/t) % 10;
temp[k][order[k]] = arr[i];
order[k]++;
}
p=0; //p is the footmark of a in a sorting process
for(i=0;i<n;i++)
{
if(order[i] != 0)
{
for(j=0;j<order[i];j++)
{
arr[p] = temp[i][j];
p++;
}
order[i] = 0;
}
}
t *= 10;
}
return arr;
/********** End **********/
}