1. Time Complexity
1. Complexity: A measure of the efficiency of an algorithm
2. Concept: Time complexity mainly measures the speed of an algorithm, the number of basic operations in the algorithm, which is the time complexity of the algorithm.
3. Representation: in large O notation
// Please calculate how many times the func1 basic operation has been performed?
void func1(int N){
int count = 0;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N ; j++) {//N*N
count++;
}
}
for (int k = 0; k < 2 * N ; k++) {//2N
count++;
}
int M = 10;
while ((M--) > 0) {//10
count++;
}
System.out.println(count);
}Calculated: func1 basic operation performed (N^2+2N+10)
When we calculate time complexity, we don't really have to calculate the exact number of executions, but only the approximate number of executions, so we derive the large order O method:
a. Using constants
1
Replace all additive constants in run time.
b. In the modified number of runs function, only the highest order items are retained.
c. If the highest order term exists and is not
1
, the constant multiplied by this item is removed. The result is big
Order O.
So fun1's time complexity is O(N^2)--->worst case
Some algorithms have the best, average, and worst case time complexity:
Worst case: Maximum number of runs of any input size (upper bound)
Average case: Expected number of runs of any input size
Best case: Minimum number of runs of any input size (lower bound)
For example, find a data x in an array of length n.
Best case: once found
Worst case: n times found
Average: n/2 times found
3. Examples of common time complexity algorithms
Example 1:
// Calculate the time complexity of func2?
void func2(int N) {
int count = 0;
for (int k = 0; k < 2 * N ; k++) {//2N
count++; }
int M = 10;
while ((M--) > 0) {//10
count++; }
System.out.println(count);
}
//2N+10->NSo its time complexity is O(N)
Example 2:
// Calculate the time complexity of func3?
void func3(int N, int M) {
int count = 0;
for (int k = 0; k < M; k++) {//M
count++; }
for (int k = 0; k < N ; k++) {//N
count++; }
System.out.println(count);
}M and N are both unknown, so their time complexity is O (M+N)
Example 3:
// Calculate the time complexity of func4?
void func4(int N) {
int count = 0;
for (int k = 0; k < 100; k++) {//100
count++; }
System.out.println(count);
}
//100->1All constant terms are replaced by 1, so its time complexity is O(1)
Example 4 (bubble sort):
// Calculate the time complexity of bubbleSort?
void bubbleSort(int[] array) {
for (int end = array.length; end > 0; end--) {//N
boolean sorted = true;
for (int i = 1; i < end; i++) {//N(N-1)
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
//N(N-1)=N^2-N->N^2So its time complexity is O (N^2), which is best of all its time complexity. Its best time complexity is O (N), which is equivalent to ordering i only once.
Example 5 (Binary Search):
// Compute the time complexity of binarySearch?
int binarySearch(int[] array, int value) {
int begin = 0;
int end = array.length - 1;
while (begin <= end) {
int mid = begin + ((end-begin) / 2);
if (array[mid] < value)
begin = mid + 1;
else if (array[mid] > value)
end = mid - 1;
else
return mid;
}
return -1; }
Basic operations performed best once, worst O(logN) times, and time complexity O(logN) ps:logN is represented by a base of 2 and a logarithm of N in algorithm analysis. Some places are written as lgN. Because each dichotomy search excludes half of the unsuitable values, one dichotomy remains: n/2 Two dichotomies remain: n/2/2 = n/4
Example 6:
// Calculate the time complexity of factorial recursion factorial?
long factorial(int N) {
return N < 2 ? N : factorial(N-1) * N; }
Recursive Time Complexity=Number of Recursions*Number of Operations After Each Recursion=N*1
Through computational analysis, it is found that the basic operation recurs N times and the time complexity is O(N)
Example 7:
// Calculate the time complexity of fibonacci recursion?
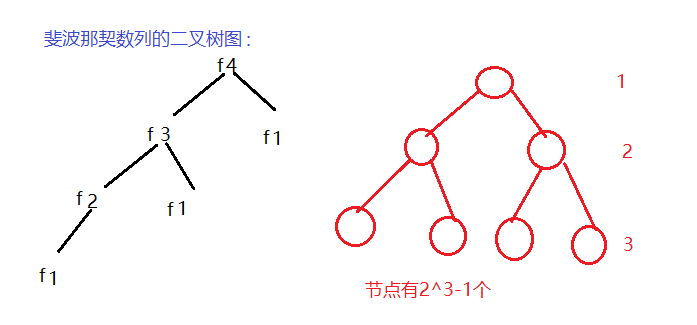
int fibonacci(int N) {
return N < 2 ? N : fibonacci(N-1)+fibonacci(N-2);
}
Recursive Time Complexity=Number of Recursions*Number of Operations After Each Recursion=2^N*1
Computational analysis reveals that the basic operation recurs 2^N times with a time complexity of O(2^N).
Computing the time complexity of an algorithm is not only a matter of code, but also a matter of thought.
2. Spatial Complexity
1. Spatial Complexity measures the extra space required by an algorithm. Spatial Complexity counts the number of variables
2. Representation: expressed by large O asymptotic method
3. Examples of common spatial complexity algorithms
Example 1:
// Calculate the spatial complexity of bubbleSort?
void bubbleSort(int[] array) {//1
for (int end = array.length; end > 0; end--) {
boolean sorted = true;
for (int i = 1; i < end; i++) {
if (array[i - 1] > array[i]) {
Swap(array, i - 1, i);
sorted = false;
}
}
if (sorted == true) {
break;
}
}
}
// Compute the spatial complexity of fibonacci?
int[] f
It only has one variable array, so its spatial complexity is O(1)
Example 2:
// Compute the spatial complexity of fibonacci?
int[] fibonacci(int n) {
long[] fibArray = new long[n + 1];
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; i++) {
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray; }fibonacci has N spaces to store each recursive value, so its spatial complexity is O(N)
Example 3:
// Calculate the time complexity of factorial recursive Factorial?
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N; }N calls were made recursively, opening up N stack frames, each using N constant spaces. Spatial complexity is O(N)