Tiimmi's learning log 2

Two days of deduction, one question a day

2021.11.3 punch in

Today, I spent most of my time studying QQ robot. I don't have time to see many things. I don't do much today.

Li Kou daily question 2021.11.3

Connected to rainwater II [difficult]

Give you a matrix of m x n, where the values are non negative integers, representing the height of each cell in the two-dimensional height map. Please calculate the maximum volume of rainwater that can be received by the shape in the map.

Example:

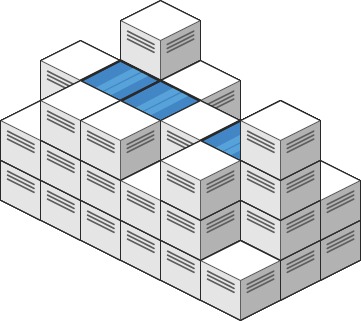
input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
output: 4
 explain: After the rain, the rain will be in the blue box above. The total amount of rainwater is 1+2+1=4. 

Source: LeetCode
Link: https://leetcode-cn.com/problems/trapping-rain-water-ii
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

• Analysis: there are still no ideas to solve the difficulties. Please attach the official ideas and solutions:

Method 1: minimum heap


First, let's think about what kind of box can catch water:

The box is not the outermost box;
The height of the block itself is lower than that of the four adjacent blocks above, below, left and right after receiving water;
We assume that the index of the block is (i,j)(i,j), the height of the block is hightmap [i] [J], and the height of the block after receiving water is water[i][j]. Then we know that the height of block (i,j)(i,j) after water connection is:

water[i][j]=max(heightMap[i][j],min(water[i−1][j],water[i+1][j],water[i][j−1],water[i][j+1]))

We know that the calculation formula of the actual water receiving capacity of block (i,j)(i,j) is water[i][j] - heightMap[i][j]
First, we can determine that the height of the outermost block of the matrix after receiving water is the height of the block itself. Because the outermost block cannot receive water, the outermost block water [i] [J] = highmap [i] [J].

According to the principle of wooden barrel, the height of rainwater received is determined by the shortest wooden board around the container. We can know that the height of water in the container depends on the block with the lowest height of the outermost layer, as shown in Figure 1:

Assuming that we have known the minimum value of the water receiving height of the outermost block, we can certainly determine the water receiving height of the adjacent blocks of the minimum height block according to the barrel principle. At the same time, we update the mark of the outermost block. We find the minimum value of the height after water connection again in the new outermost block, and determine the water connection height of its adjacent block, as shown in Figure 2:

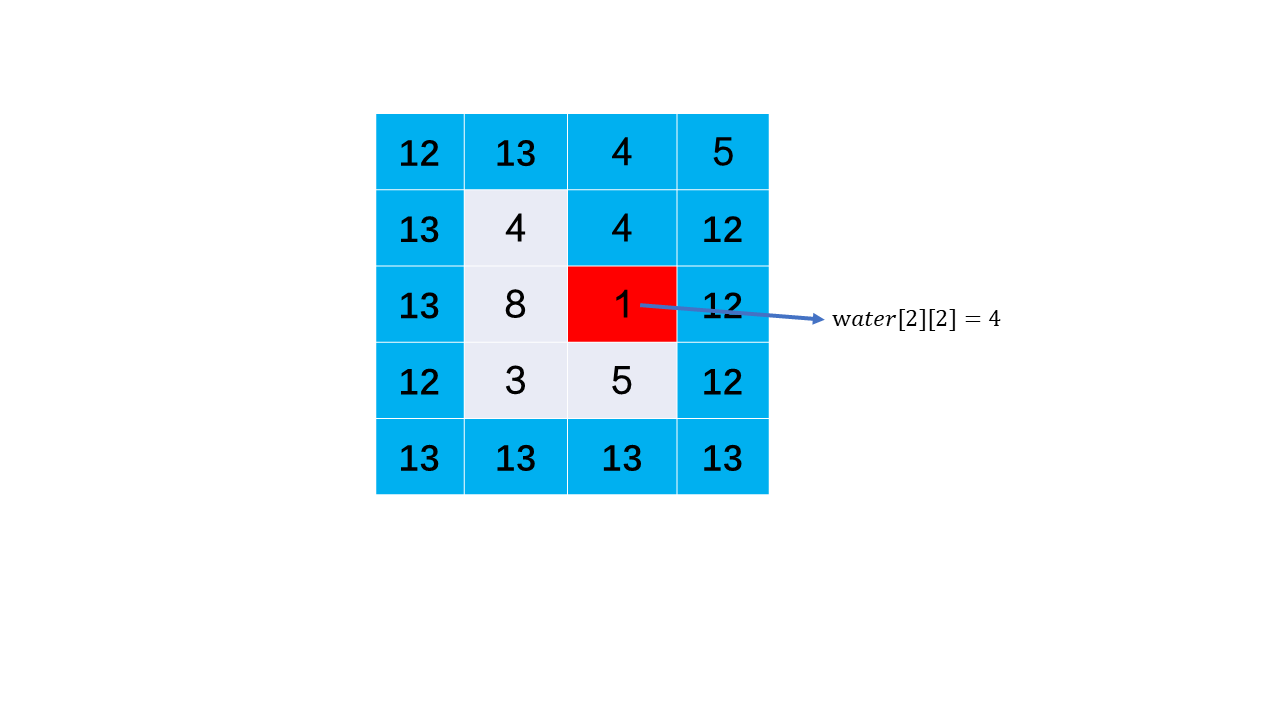
Then update the outermost layer again and iterate successively until the water receiving height of all blocks is calculated, so as to know the water receiving capacity in the matrix.

Author: leetcode solution
Link: https://leetcode-cn.com/problems/trapping-rain-water-ii/solution/jie-yu-shui-ii-by-leetcode-solution-vlj3/
Source: LeetCode
The copyright belongs to the author. For commercial reprint, please contact the author for authorization, and for non-commercial reprint, please indicate the source.

• code:

class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        if len(heightMap) <= 2 or len(heightMap[0]) <= 2:
            return 0

        m, n = len(heightMap), len(heightMap[0])
        visited = [[0 for _ in range(n)] for _ in range(m)]
        pq = []
        for i in range(m):
            for j in range(n):
                if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                    visited[i][j] = 1
                    heapq.heappush(pq, (heightMap[i][j], i * n + j))
        
        res = 0
        dirs = [-1, 0, 1, 0, -1]
        while pq:
            height, position = heapq.heappop(pq)
            for k in range(4):
                nx, ny = position // n + dirs[k], position % n + dirs[k + 1]
                if nx >= 0 and nx < m and ny >= 0 and ny < n and visited[nx][ny] == 0:
                    if height > heightMap[nx][ny]:
                        res += height - heightMap[nx][ny]
                    visited[nx][ny] = 1    
                    heapq.heappush(pq, (max(height, heightMap[nx][ny]), nx * n + ny))
        return res

2021.11.4 punch in

I still don't have much energy today. Try again tomorrow. jpg (I have to take time to write a blog, and the time utilization efficiency is not enough...)

Li Kou daily question 2021.11.4

367. Effective complete square [simple]

Difficult questions are submissive, simple questions I hit hard
Given a positive integer num, write a function. If num is a complete square number, it returns true, otherwise it returns false.

Advanced: do not use any built-in library functions, such as sqrt.

• Analysis: it's easy to think of dichotomy if you don't use the built-in library or search

  Dichotomy needs to pay attention to the reduction of left and right boundaries and termination conditions

• Algorithm process:

  1. Left boundary = 1, right boundary = num, mid = (left + right) // 2;
  2. Compare the mid square with num to determine the size
  3. Larger than num, indicating that the answer is in the [left, mid] interval, right = mid - 1
  4. Smaller than num, indicating that the answer is in the [mid, right] interval, left = mid + 1
  5. Equal to num, mid is the answer and returns True
  6. False if no answer is found

• code:

class Solution:
    def isPerfectSquare(self, num: int) -> bool:
        left, right = 1, num
        while left <= right:
            mid = (left + right) // 2
            if mid * mid < num:
                left = mid + 1
            elif mid * mid > num:
                right = mid - 1
            else:
                return True
        return False