Algorithmic Base-Tree
Three ways to traverse a tree (recursive)
The three recursive traversals of trees are based on recursive order. The so-called recursive order is that each node returns to that node three times if it uses recursion. For example: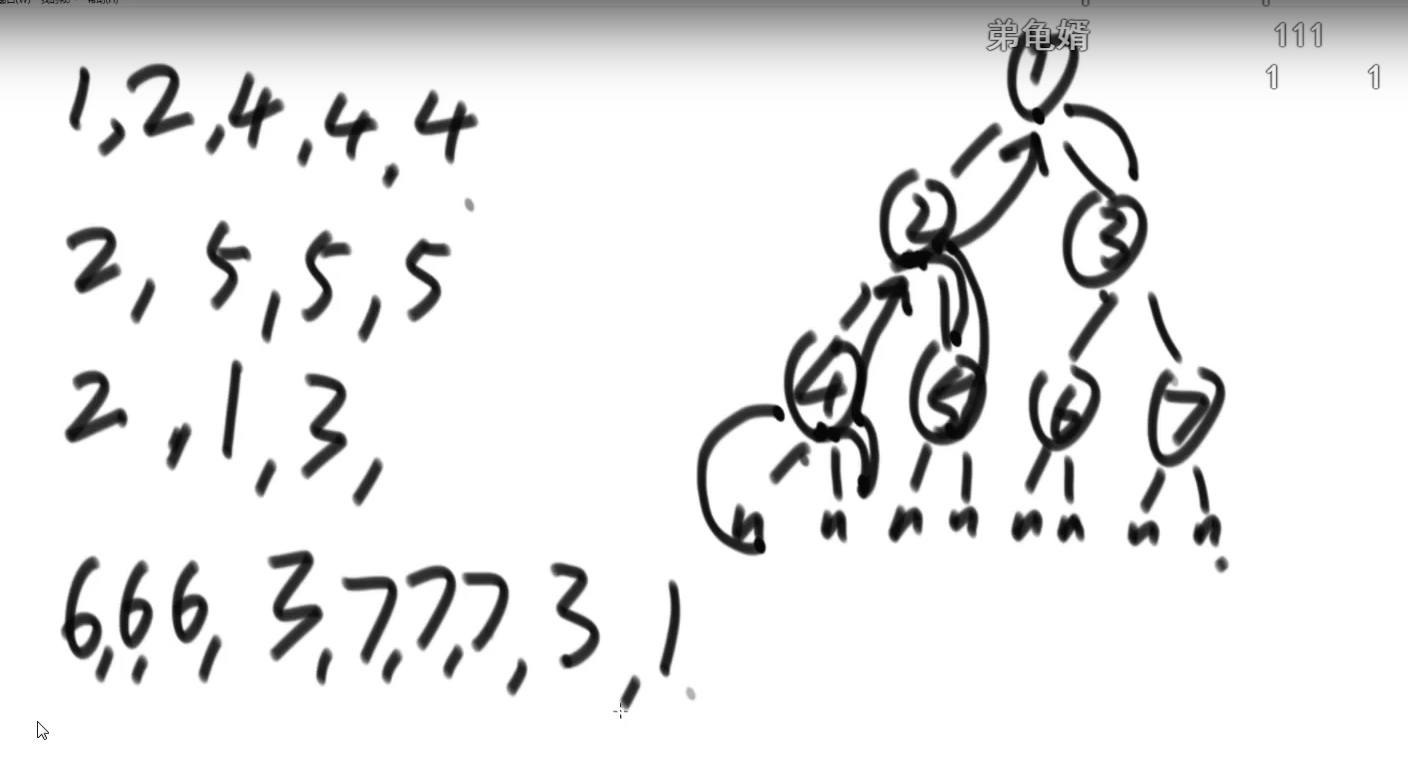
The so-called recursive order is that each node traverses three times, so when using recursion, all nodes are traversed in order when they are first visited, and all nodes are traversed in order when they are printed the second time. All nodes are traversed in the last order when they are printed
import java.util.Stack;
public class Code01_PreInPosTraversal {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
}
Three ways to traverse a tree (non-recursive)
All recursive methods can be implemented in a non-recursive manner. Because recursion is all about using the stack of functions to store information, we can also implement it by requesting the corresponding data structure
- Pre-order traversal
First pop the node stack Print the node contents of a stack Stack the child nodes of a pop-stack node right-to-left Repeat until there are no elements in the stack
- Intermediate traversal
Add all the left child nodes of the node to the stack, When there is no left child node, a node element pops up. To see if this pop-up node has right children, If so, add the right child node to the stack. Because this element is now a stacked element, all the left children of this element need to be added to the stack. Print elements until all elements are ejected
- Post-order traversal
First pop the node stack Put the pop-up elements on a new stack Stack the child nodes of a pop-stack node left-to-right Repeat until there are no elements in the stack Printing elements in a new stack is a postorder traversal
package class05;
import java.util.Stack;
public class Code01_PreInPosTraversal {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
public static void posOrderUnRecur1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
public static void posOrderUnRecur2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack<Node> stack = new Stack<Node>();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
stack.push(c.left);
} else if (c.right != null && h != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
public static void main(String[] args) {
Node head = new Node(5);
head.left = new Node(3);
head.right = new Node(8);
head.left.left = new Node(2);
head.left.right = new Node(4);
head.left.left.left = new Node(1);
head.right.left = new Node(7);
head.right.left.left = new Node(6);
head.right.right = new Node(10);
head.right.right.left = new Node(9);
head.right.right.right = new Node(11);
// recursive
System.out.println("==============recursive==============");
System.out.print("pre-order: ");
preOrderRecur(head);
System.out.println();
System.out.print("in-order: ");
inOrderRecur(head);
System.out.println();
System.out.print("pos-order: ");
posOrderRecur(head);
System.out.println();
// unrecursive
System.out.println("============unrecursive=============");
preOrderUnRecur(head);
inOrderUnRecur(head);
posOrderUnRecur1(head);
posOrderUnRecur2(head);
}
}
Width traversal of trees
Binary tree depth-first traversal and width-first traversal, binary tree depth-first traversal is binary tree priority traversal, what is binary tree width-first traversal?
Width traversal uses queue, first put the head node in the stack, first left, then right, then pop-up for the next week, that is, put a node in the queue, when the pop-up node first put the left node and then the right node, then the pop-up will put the left node and then the right node.
The calculation of which layer has the most nodes is to traverse with width first, but when putting nodes in the queue, you need to record the number of layers where the nodes are located first!
package class05;
import java.util.HashMap;
import java.util.LinkedList;
public class Code03_TreeMaxWidth {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static int getMaxWidth(Node head) {
if (head == null) {
return 0;
}
int maxWidth = 0;
int curWidth = 0;
int curLevel = 0;
HashMap<Node, Integer> levelMap = new HashMap<>();
levelMap.put(head, 1);
LinkedList<Node> queue = new LinkedList<>();
queue.add(head);
Node node = null;
Node left = null;
Node right = null;
while (!queue.isEmpty()) {
node = queue.poll();
left = node.left;
right = node.right;
if (left != null) {
levelMap.put(left, levelMap.get(node) + 1);
queue.add(left);
}
if (right != null) {
levelMap.put(right, levelMap.get(node) + 1);
queue.add(right);
}
if (levelMap.get(node) > curLevel) {
curWidth = 0;
curLevel = levelMap.get(node);
} else {
curWidth++;
}
maxWidth = Math.max(maxWidth, curWidth);
}
return maxWidth;
}
public static void main(String[] args) {
// TODO Auto-generated method stub
}
}
Visual Print Tree
package class05;
import java.util.Stack;
public class Code01_PreInPosTraversal {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static void preOrderRecur(Node head) {
if (head == null) {
return;
}
System.out.print(head.value + " ");
preOrderRecur(head.left);
preOrderRecur(head.right);
}
public static void inOrderRecur(Node head) {
if (head == null) {
return;
}
inOrderRecur(head.left);
System.out.print(head.value + " ");
inOrderRecur(head.right);
}
public static void posOrderRecur(Node head) {
if (head == null) {
return;
}
posOrderRecur(head.left);
posOrderRecur(head.right);
System.out.print(head.value + " ");
}
public static void preOrderUnRecur(Node head) {
System.out.print("pre-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while (!stack.isEmpty()) {
head = stack.pop();
System.out.print(head.value + " ");
if (head.right != null) {
stack.push(head.right);
}
if (head.left != null) {
stack.push(head.left);
}
}
}
System.out.println();
}
public static void inOrderUnRecur(Node head) {
System.out.print("in-order: ");
if (head != null) {
Stack<Node> stack = new Stack<Node>();
while (!stack.isEmpty() || head != null) {
if (head != null) {
stack.push(head);
head = head.left;
} else {
head = stack.pop();
System.out.print(head.value + " ");
head = head.right;
}
}
}
System.out.println();
}
public static void posOrderUnRecur1(Node head) {
System.out.print("pos-order: ");
if (head != null) {
Stack<Node> s1 = new Stack<Node>();
Stack<Node> s2 = new Stack<Node>();
s1.push(head);
while (!s1.isEmpty()) {
head = s1.pop();
s2.push(head);
if (head.left != null) {
s1.push(head.left);
}
if (head.right != null) {
s1.push(head.right);
}
}
while (!s2.isEmpty()) {
System.out.print(s2.pop().value + " ");
}
}
System.out.println();
}
public static void posOrderUnRecur2(Node h) {
System.out.print("pos-order: ");
if (h != null) {
Stack<Node> stack = new Stack<Node>();
stack.push(h);
Node c = null;
while (!stack.isEmpty()) {
c = stack.peek();
if (c.left != null && h != c.left && h != c.right) {
stack.push(c.left);
} else if (c.right != null && h != c.right) {
stack.push(c.right);
} else {
System.out.print(stack.pop().value + " ");
h = c;
}
}
}
System.out.println();
}
public static void main(String[] args) {
Node head = new Node(5);
head.left = new Node(3);
head.right = new Node(8);
head.left.left = new Node(2);
head.left.right = new Node(4);
head.left.left.left = new Node(1);
head.right.left = new Node(7);
head.right.left.left = new Node(6);
head.right.right = new Node(10);
head.right.right.left = new Node(9);
head.right.right.right = new Node(11);
// recursive
System.out.println("==============recursive==============");
System.out.print("pre-order: ");
preOrderRecur(head);
System.out.println();
System.out.print("in-order: ");
inOrderRecur(head);
System.out.println();
System.out.print("pos-order: ");
posOrderRecur(head);
System.out.println();
// unrecursive
System.out.println("============unrecursive=============");
preOrderUnRecur(head);
inOrderUnRecur(head);
posOrderUnRecur1(head);
posOrderUnRecur2(head);
}
}