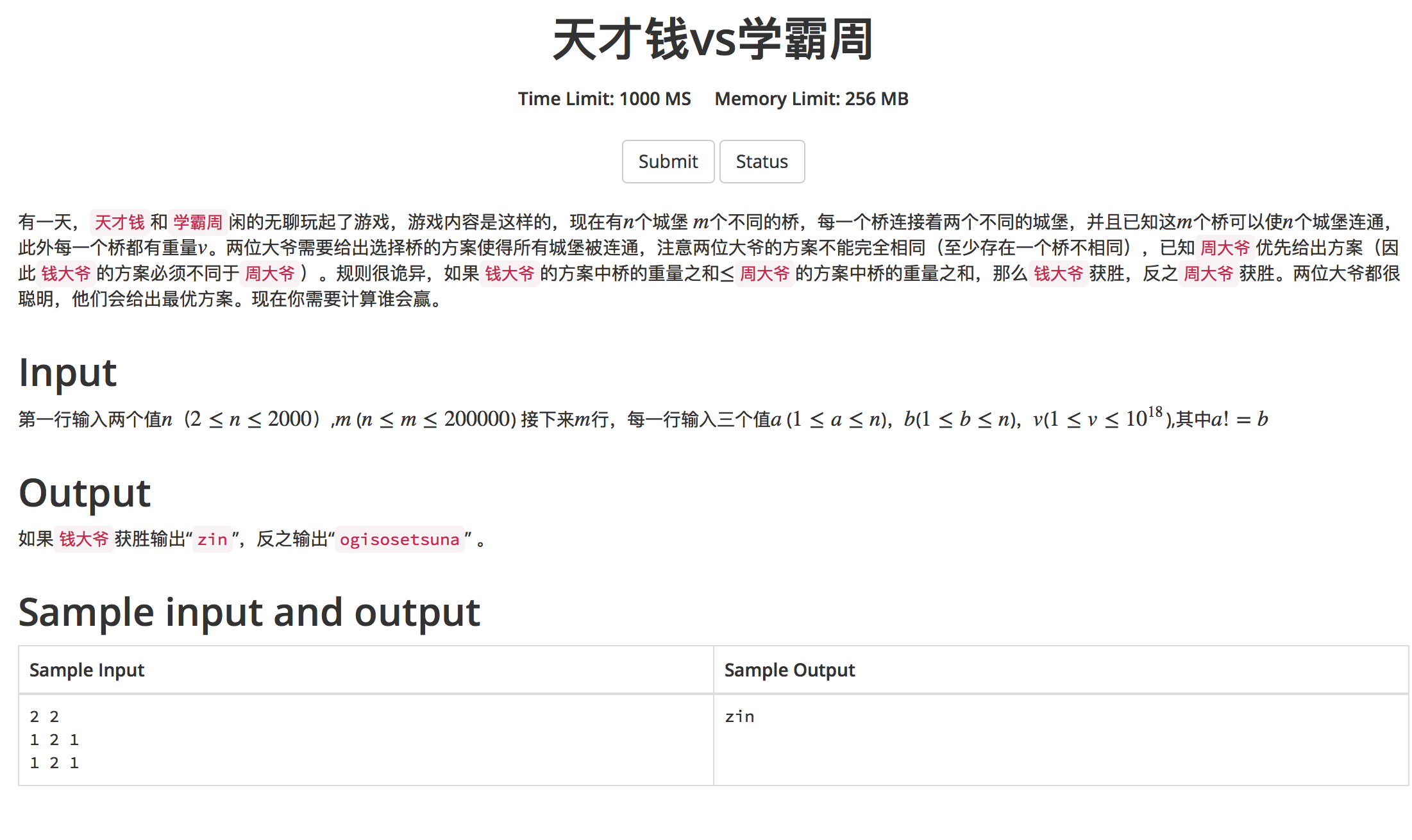
The example should be wrong. This problem is probably to find out whether the minimum spanning tree is unique, that is, to find the secondary small spanning tree. For a minimum spanning tree, the only way to determine whether it is unique is to enumerate two points on the minimum spanning tree. Because it is a tree, after two points are linked to one, it must be a ring. For this ring, we deal with the largest edge of the ring , delete the largest edge of this ring, and you will get a tree, because you delete the largest edge (this edge can no longer be within the minimum spanning tree.) , so if the sum of the weight of the left tree is equal to the minimum spanning tree, then the minimum spanning tree must not be unique.

Because there are not many points in the topic, we choose prim algorithm to find the minimum spanning tree, and then enumerate to judge.

The code is as follows

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 2e3 + 5;
LL G[maxn][maxn],edge[maxn][maxn],path[maxn][maxn];
LL dis[maxn];
LL ans;
int vis[maxn],pre[maxn];
int n,m;
LL prim(){
    for (int i=1; i<=n; i++) {
        dis[i] = G[1][i];
        pre[i] = 1;
    }
    pre[1] = 0; dis[1] = 0; vis[1] = 1;
    for (int i=2; i<=n; i++) {
        LL val = LLONG_MAX,v = 0;
        for (int j=1; j<=n; j++) {
            if (!vis[j] && dis[j] < val){
                val = dis[j];
                v = j;
            }
        }
        ans += val; vis[v] = 1;
        edge[v][pre[v]] = edge[pre[v]][v] = 1;
        for (int j=1; j<=n; j++) {
            if (vis[j]) path[j][v] = path[v][j] = max(path[j][pre[v]],dis[v]);
            if (!vis[j] && dis[j] > G[v][j]){
                dis[j] = G[v][j];
                pre[j] = (int)v;
            }
        }
    }
    return ans;
}
void solve(){
    LL dist = prim();
    int tag = 0;
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=n; j++) {
            if (G[i][j] != LLONG_MAX && !edge[i][j] && i != j && dist - G[i][j] + path[i][j] == dist){
                tag = 1; break;
            }
        }
    }
    if (tag){
        cout << "zin" << endl;
    }else{
        cout << "ogisosetsuna" << endl;
    }
}
int main(){
    LL a,b,v;
    scanf("%d%d",&n,&m);
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=n; j++) {
            if (i != j)
                G[i][j] = G[j][i] = LLONG_MAX;
            else
                G[i][j] = G[j][i] = 0;
        }
    }
    for (int i=0; i<m; i++) {
        scanf("%lld%lld%lld",&a,&b,&v);
        G[a][b] = G[b][a] = v;
    }
    solve();
    return 0;
}