5. (6') Code Fill-in
To transpose a square matrix is to change the original row number to the column number and the original column number to the row number.
For example, the following matrix:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
After transposition, it becomes:
1 5 9 13
2 6 1014
3 7 1115
4 8 1216
However, if the square matrix is rotated clockwise (not transposed), the results are as follows:
13 9 5 1
14 10 6 2
15 11 7 3
16 12 8 4
The following code implements the function of rotating a square clockwise.
After filling in the blank, the code:
#include <stdio.h>
#include <stdlib.h>
void rotate(int* x, int rank)
{
int* y = (int*)malloc(rank*sizeof(x)); // Fill in the blanks
int i;
for(int i=0; i<rank * rank; i++)
{
y[rank -1 - i/rank + rank * (i%rank)] = x[i]; // Fill in the blanks
}
for(i=0; i<rank*rank; i++)
{
x[i] = y[i];
}
free(y);
}
int main(int argc, char* argv[])
{
int x[4][4] = {{1,2,3,4},{5,6,7,8},{9,10,11,12},{13,14,15,16}};
int rank = 4;
rotate(&x[0][0], rank);
for(int i=0; i<rank; i++)
{
for(int j=0; j<rank; j++)
{
printf("%4d", x[i][j]);
}
printf("\n");
}
return 0;
}
6. (9') Code filling
For 32-bit word-length machines, about 2 billion words, it is impossible to express them with int type. We can choose int64 type, but no matter how extended, fixed integer type always has the limit of expression! What if super large integers are calculated accurately? A simple way is to use only the existing types, but the operation of large integers into a number of small integers, that is, the so-called "block method".
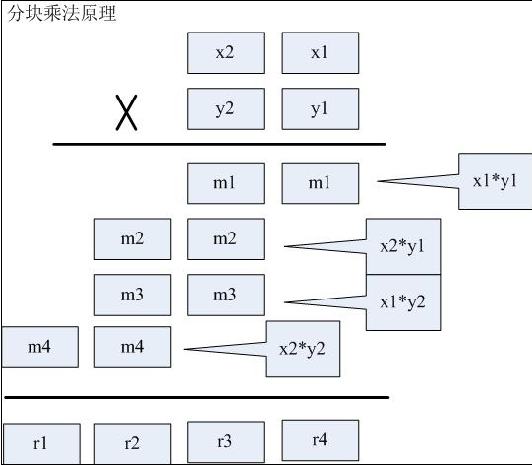
Fig. [1.jpg] shows the principle of block multiplication. It is possible to divide a large number into several segments (2 segments here) of decimal numbers, and then express a large number by multiple combinations of decimal operations. According to the carrying capacity of int, the size of small blocks can be specified. For example, if the int is divided into two segments, the upper limit value of small blocks can be 10000. Note that the carry correction is required after the vertical accumulation of small blocks.
The following code illustrates the principle of block multiplication (multiplier and multiplier are divided into two segments).
After filling in the blank, the code:
#include <stdio.h>
void bigmul(int x, int y, int r[])
{
int base = 10000;
int x2 = x / base;
int x1 = x % base;
int y2 = y / base;
int y1 = y % base;
int n1 = x1 * y1;
int n2 = x1 * y2;
int n3 = x2 * y1;
int n4 = x2 * y2;
r[3] = n1 % base;
r[2] = n1 / base + n2 % base + n3 % base;
r[1] = n2 / base + n3 / base + n4 % base; // Fill in the blanks
r[0] = n4 / base;
r[1] += r[2] / base; // Fill in the blanks
r[2] = r[2] % base;
r[0] += r[1] / base;
r[1] = r[1] % base;
}
int main(int argc, char* argv[])
{
int x[] = {0,0,0,0};
bigmul(87654321, 12345678, x);
printf("%d%d%d%d\n", x[0],x[1],x[2],x[3]);
return 0;
}
7. (13') Code filling
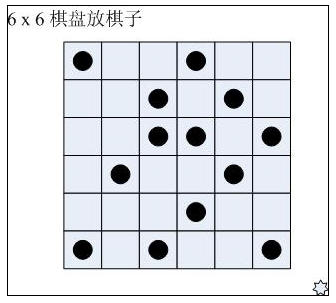
There are 6 x 6 checkerboards today. Some of the lattices have been pre-arranged. Now let's put some more on it so that there are exactly three pieces in each row and column. We hope to work out all possible releases. The following code implements this function.
In the initial array, "1" means that there are chess pieces, and "0" means blank.
After filling in the blank, the code:
#include <stdio.h>
int N = 0;
bool CheckStoneNum(int x[][6])
{
for(int k=0; k<6; k++)
{
int NumRow = 0;
int NumCol = 0;
for(int i=0; i<6; i++)
{
if(x[k][i]) NumRow++;
if(x[i][k]) NumCol++;
}
if(NumRow!=3 || NumCol!=3) return false; // Fill in the blanks
}
return true;
}
int GetRowStoneNum(int x[][6], int r)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[r][i]) sum++;
return sum;
}
int GetColStoneNum(int x[][6], int c)
{
int sum = 0;
for(int i=0; i<6; i++) if(x[i][c]) sum++;
return sum;
}
void show(int x[][6])
{
for(int i=0; i<6; i++)
{
for(int j=0; j<6; j++) printf("%2d", x[i][j]);
printf("\n");
}
printf("\n");
}
void f(int x[][6], int r, int c);
void GoNext(int x[][6], int r, int c)
{
if(c<6)
f(x, r, c+1); // Fill in the blanks
else
f(x, r+1, 0);
}
void f(int x[][6], int r, int c)
{
if(r==6)
{
if(CheckStoneNum(x))
{
N++;
show(x);
}
return;
}
if(x[r][c]) // Chess pieces have been played.
{
GoNext(x,r,c);
return;
}
int rr = GetRowStoneNum(x,r);
int cc = GetColStoneNum(x,c);
if(cc>=3) // This column is full.
GoNext(x,r,c);
else if(rr>=3) // Our bank is full.
f(x, r+1, 0);
else
{
x[r][c] = 1;
GoNext(x,r,c);
x[r][c] = 0;
if(!(3-rr >= 6-c || 3-cc >= 6-r)) // If there are serious deficiencies in this line or column, the benchmark should not be empty! __________
GoNext(x,r,c);
}
}
int main(int argc, char* argv[])
{
int x[6][6] = {
{1,0,0,0,0,0},
{0,0,1,0,1,0},
{0,0,1,1,0,1},
{0,1,0,0,1,0},
{0,0,0,1,0,0},
{1,0,1,0,0,1}
};
f(x, 0, 0);
printf("%d\n", N);
return 0;
}